Examen simulacro IPN Matemáticas CSyA: Reactivos del 11 al 20

Hola de nuevo aspirante, seguimos con los reactivos del 11 al 20 en esta tercera parte del examen simulador de matemáticas para carreras del área de ciencias sociales y administrativas.

Recuerda medir tu tiempo en cada intento, además de anotar los ejercicios y temas que más se te compliquen.

Reactivo 11

Simplifica la siguiente expresión algebraica.

\frac{\sqrt[6]{18{x}^{3}{y}^{4}{z}^{5}}}{\sqrt[4]{3{x}^{2}{y}^{2}{z}^{3}}}

1. \sqrt[12]{12\cdot {y}^{2}\cdot z}
2. \sqrt[6]{12\cdot {y}^{2}\cdot z}
3. \sqrt[12]{{y}^{2}\cdot z}
4. \sqrt[12]{6\cdot {y}^{2}\cdot z}

Solución:

Comenzamos separando a la raíz en cada uno de los factores.

\frac{\sqrt[6]{18{x}^{3}{y}^{4}{z}^{5}}}{\sqrt[4]{3{x}^{2}{y}^{2}{z}^{3}}}=\frac{\sqrt[6]{18}\sqrt[6]{{x}^{3}}\sqrt[6]{{y}^{4}}\sqrt[6]{{z}^{5}}}{\sqrt[4]{3}\sqrt[4]{{x}^{2}}\sqrt[4]{{y}^{2}}\sqrt[4]{{z}^{3}}}

Ahora, expresamos a los radicales en forma de potencia. Al coeficiente numérico del numerador lo separamos como \sqrt[6]{18}=\sqrt[6]{2}\sqrt[6]{{3}^{2}} .

\frac{\sqrt[6]{18}\sqrt[6]{{x}^{3}}\sqrt[6]{{y}^{4}}\sqrt[6]{{z}^{5}}}{\sqrt[4]{3}\sqrt[4]{{x}^{2}}\sqrt[4]{{y}^{2}}\sqrt[4]{{z}^{3}}}=\frac{{2}^{1/6}{3}^{2/6}{x}^{3/6}{y}^{4/6}{z}^{5/6}}{{3}^{1/4}{x}^{2/4}{y}^{2/4}{z}^{3/4}}

Ahora, simplificamos aplicando el cociente de potencias de igual base.

\frac{{2}^{1/6}{3}^{2/6}{x}^{3/6}{y}^{4/6}{z}^{5/6}}{{3}^{1/4}{x}^{2/4}{y}^{2/4}{z}^{3/4}}={2}^{1/6}\cdot {3}^{\frac{1}{3}-\frac{1}{4}}\cdot {x}^{\frac{1}{2}-\frac{1}{2}}\cdot {y}^{\frac{2}{3}-\frac{1}{2}}\cdot {z}^{\frac{5}{6}-\frac{3}{4}}

Simplificamos los exponentes.

{2}^{1/6}\cdot {3}^{\frac{1}{3}-\frac{1}{4}}\cdot {x}^{\frac{1}{2}-\frac{1}{2}}\cdot {y}^{\frac{2}{3}-\frac{1}{2}}\cdot {z}^{\frac{5}{6}-\frac{3}{4}}={2}^{\frac{1}{6}}\cdot {3}^{\frac{1}{12}}\cdot {x}^{0}\cdot {y}^{\frac{1}{6}}\cdot {z}^{\frac{1}{12}}={2}^{\frac{1}{6}}\cdot {3}^{\frac{1}{12}}\cdot {y}^{\frac{1}{6}}\cdot {z}^{\frac{1}{12}}

A las potencias con exponente \frac{1}{6} , se pueden expresar como \frac{2}{12} .

{2}^{\frac{1}{6}}\cdot {3}^{\frac{1}{12}}\cdot {y}^{\frac{1}{6}}\cdot {z}^{\frac{1}{12}}={2}^{\frac{2}{12}}\cdot {3}^{\frac{1}{12}}\cdot {y}^{\frac{2}{12}}\cdot {z}^{\frac{1}{12}}

Convirtiendo todo a raíz con índice 12 obtenemos:

{2}^{\frac{2}{12}}\cdot {3}^{\frac{1}{12}}\cdot {y}^{\frac{2}{12}}\cdot {z}^{\frac{1}{12}}=\sqrt[12]{{2}^{2}\cdot 3\cdot {y}^{2}\cdot z}=\sqrt[12]{12\cdot {y}^{2}\cdot z}

Finalmente:

\frac{\sqrt[6]{18{x}^{3}{y}^{4}{z}^{5}}}{\sqrt[4]{3{x}^{2}{y}^{2}{z}^{3}}}=\sqrt[12]{12\cdot {y}^{2}\cdot z}

Concluimos que la respuesta correcta es el inciso a).

Reactivo 12

Indique el número que cumple con la siguiente descripción:

La tercera potencia del incremento de un número dividida por dicho número decrementado uno.

1. \frac{{\left(x+1\right)}^{3}}{x-1}
2. \frac{{\left(x-1\right)}^{3}}{x+1}
3. {\left(\frac{x+1}{x-1}\right)}^{3}
4. \frac{x+1}{{\left(x-1\right)}^{3}}

Solución:

Examinando la frase del enunciado, identificamos que se describe a una fracción. En el numerador se encuentra una potencia y en el denominador a un binomio. La primera frase nos da información acerca del numerador:

La tercera potencia del incremento de un número…

La potencia del numerador tiene como exponente 3 y como base a x+1 . Esto quedaría escrito de la siguiente forma:

{\left(x+1\right)}^{3}

Ahora, el denominador se describe en la segunda parte de la frase:

…por dicho número decrementado uno.

Se refiere a la x menos 1. La fracción completa sería:

\frac{{\left(x+1\right)}^{3}}{x-1}

Concluimos el problema indicando como respuesta correcta al inciso a).

Reactivo 13

Encuentra la forma factorizada de la siguiente expresión.

\sqrt[6]{x}-\sqrt[8]{y}

1. \left({x}^{\frac{1}{12}}+{y}^{\frac{1}{16}}\right)
2. \left({x}^{\frac{1}{12}}+{y}^{\frac{1}{16}}\right)\left({x}^{\frac{1}{12}}-{y}^{\frac{1}{16}}\right)
3. \left({x}^{\frac{1}{12}}-{y}^{\frac{1}{16}}\right)
4. \left({x}^{\frac{1}{3}}+{y}^{\frac{1}{4}}\right)\left({x}^{\frac{1}{3}}-{y}^{\frac{1}{4}}\right)

Solución:

Iniciamos expresando a los radicales como potencias de exponente fraccionario.

\sqrt[6]{x}-\sqrt[8]{y}={x}^{\frac{1}{6}}-{y}^{\frac{1}{8}}

Ahora, multiplicamos y dividimos a los exponentes por 2.

{x}^{\frac{1}{6}}-{y}^{\frac{1}{8}}={x}^{\frac{2}{12}}-{y}^{\frac{2}{16}}

Aplicamos potencia de una potencia.

{x}^{\frac{2}{12}}-{y}^{\frac{2}{16}}={\left({x}^{\frac{1}{12}}\right)}^{2}-{\left({y}^{\frac{1}{16}}\right)}^{2}

Finalmente, aplicamos diferencia de cuadrados.

{\left({x}^{\frac{1}{12}}\right)}^{2}-{\left({y}^{\frac{1}{16}}\right)}^{2}=\left({x}^{\frac{1}{12}}+{y}^{\frac{1}{16}}\right)\left({x}^{\frac{1}{12}}-{y}^{\frac{1}{16}}\right)

La forma factorizada del binomio es:

\sqrt[6]{x}-\sqrt[8]{y}=\left({x}^{\frac{1}{12}}+{y}^{\frac{1}{16}}\right)\left({x}^{\frac{1}{12}}-{y}^{\frac{1}{16}}\right)

Concluimos indicando como respuesta correcta al inciso b).

Reactivo 14

Resuelve el siguiente sistema de ecuaciones lineales.

\left\{\begin{array}{c}2x-y+z=2\\ x-y-z=-1\\ 5x-y-3z=1\end{array}\right.

1. \begin{array}{c}x=-3\\ z=-3\\ y=1\end{array}
2. \begin{array}{c}x=3\\ z=-3\\ y=1\end{array}
3. \begin{array}{c}x=-3\\ z=3\\ y=1\end{array}
4. \begin{array}{c}x=1\\ z=1\\ y=1\end{array}

Solución:

Para resolver este sistema de 3 ecuaciones con 3 incógnitas, tenemos 2 opciones: emplear la regla de Cramer o aplicar reducción. Debido a la extensión del SEL, el método más conveniente es la regla de Cramer.

Comenzamos calculando el determinante del sistema.

{\mathrm{\Delta }}_{s}=\left|\begin{array}{ccc}2& -1& 1\\ 1& -1& -1\\ 5& -1& -3\end{array}\right|

{\mathrm{\Delta }}_{s}=\left|\begin{array}{cc}-1& -1\\ -1& -3\end{array}\right|2-\left|\begin{array}{cc}1& -1\\ 5& -3\end{array}\right|\left(-1\right)+\left|\begin{array}{cc}1& -1\\ 5& -1\end{array}\right|\left(1\right)

{\mathrm{\Delta }}_{s}=\left(3-1\right)\left(2\right)-\left(-3+5\right)\left(-1\right)+\left(-1+5\right)=4+2+4=10

Ahora, calculamos el determinante de cada una de las variables. Se sustituye la columna de la variable con los términos independientes del sistema.

{\mathrm{\Delta }}_{x}=\left|\begin{array}{ccc}2& -1& 1\\ -1& -1& -1\\ 1& -1& -3\end{array}\right|=\left|\begin{array}{cc}-1& -1\\ -1& -3\end{array}\right|2-\left|\begin{array}{cc}-1& -1\\ 1& -3\end{array}\right|\left(-1\right)+\left|\begin{array}{cc}-1& -1\\ 1& -1\end{array}\right|\left(1\right)

{\mathrm{\Delta }}_{x}=10

{\mathrm{\Delta }}_{y}=\left|\begin{array}{ccc}2& 2& 1\\ 1& -1& -1\\ 5& 1& -3\end{array}\right|=\left|\begin{array}{cc}-1& -1\\ 1& -3\end{array}\right|2-\left|\begin{array}{cc}1& -1\\ 5& -3\end{array}\right|\left(2\right)+\left|\begin{array}{cc}1& -1\\ 5& 1\end{array}\right|\left(1\right)

{\mathrm{\Delta }}_{y}=10

{\mathrm{\Delta }}_{z}=\left|\begin{array}{ccc}2& -1& 2\\ 1& -1& -1\\ 5& -1& 1\end{array}\right|=\left|\begin{array}{cc}-1& -1\\ -1& 1\end{array}\right|2-\left|\begin{array}{cc}1& -1\\ 5& 1\end{array}\right|\left(-1\right)+\left|\begin{array}{cc}1& -1\\ 5& -1\end{array}\right|\left(2\right)

{\mathrm{\Delta }}_{z}=10

Finalmente, calculamos las coordenadas del punto que satisface al SEL.

x=\frac{{\mathrm{\Delta }}_{x}}{{\mathrm{\Delta }}_{s}}=\frac{10}{10}=1

y=\frac{{\mathrm{\Delta }}_{y}}{{\mathrm{\Delta }}_{s}}=\frac{10}{10}=1

z=\frac{{\mathrm{\Delta }}_{z}}{{\mathrm{\Delta }}_{s}}=\frac{10}{10}=1

La solución al sistema de ecuaciones es:

\begin{array}{c}x=1\\ y=1\\ z=1\end{array}

La respuesta correcta es el inciso d).

Reactivo 15

A partir del siguiente trinomio, complete cuadrados para expresarlo de la forma {\left(x+a\right)}^{2}+c .

{x}^{2}-x+5

1. {\left(x-\frac{1}{2}\right)}^{2}+\frac{19}{4}
2. {\left(x+\frac{1}{2}\right)}^{2}+\frac{19}{4}
3. {\left(x-2\right)}^{2}+\frac{19}{4}
4. {\left(x-\frac{1}{2}\right)}^{2}-\frac{19}{4}

Solución:

Al completar cuadrados, buscamos que en el trinomio se obtenga una expresión de la forma {x}^{2}\pm 2ax+{a}^{2} . Iniciamos expresando al término lineal como 2ax .

{x}^{2}-\frac{2}{2}x+5={x}^{2}-2\left(\frac{1}{2}\right)x+5

De esta forma, sabemos que a=\frac{1}{2} . Sumamos y restamos el cuadrado de \frac{1}{2} .

{x}^{2}-2\left(\frac{1}{2}\right)x+5={x}^{2}-2\left(\frac{1}{2}\right)x+\frac{1}{4}-\frac{1}{4}+5={x}^{2}-2\left(\frac{1}{2}\right)x+\frac{1}{4}+\frac{19}{4}

Aplicamos de forma inversa el producto notable {\left(x-a\right)}^{2} .

{x}^{2}-2\left(\frac{1}{2}\right)x+\frac{1}{4}+\frac{19}{4}={\left(x-\frac{1}{2}\right)}^{2}+\frac{19}{4}

Finalmente:

{x}^{2}-x+5={\left(x-\frac{1}{2}\right)}^{2}+\frac{19}{4}

Concluimos que la respuesta correcta es el inciso a).

Reactivo 16

¿Cuál de las siguientes opciones describe la siguiente expresión algebraica?

\mathrm{ln}\left(x\cdot y\right)=\mathrm{ln}x+\mathrm{ln}y

1. El logaritmo del producto de dos números es igual al logaritmo de la diferencia
2. El logaritmo del producto de dos números es igual a la diferencia de los números
3. El logaritmo del producto es igual a la suma de los logaritmos
4. El logaritmo del cociente de dos números es igual a la diferencia de los logaritmos

Solución:

En este caso, la propiedad que se aplica para obtener al miembro de la derecha es la del logaritmo del producto de dos números. Concluimos que la respuesta correcta es el inciso c).

Reactivo 17

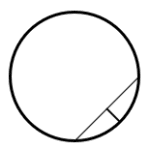
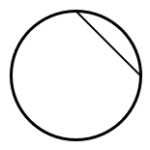
¿Cuál de las siguientes figuras representa la cuerda de la circunferencia?

1. 
2. 
3. 
4. 

Solución:

Una cuerda en la circunferencia es un segmento de recta que pasa por dos puntos, pero no por su centro. Teniendo en cuenta las imágenes de los incisos, seleccionamos como respuesta correcta al d).

Reactivo 18

La función trigonométrica \mathrm{cos}x es equivalente a:

1. \sqrt{1-{\mathrm{sin}}^{2}x}
2. \sqrt{1+{\mathrm{cos}}^{2}x}
3. \sqrt{1+{\mathrm{sec}}^{2}x}
4. \sqrt{{\mathrm{sec}}^{2}x-1}

Solución:

A partir de la identidad pitagórica, sabemos que:

{\mathrm{sin}}^{2}x+{\mathrm{cos}}^{2}x=1

Si despejamos al coseno nos queda:

{\mathrm{cos}}^{2}x=1-{\mathrm{sin}}^{2}x\to \mathrm{cos}x=\sqrt{1-{\mathrm{sin}}^{2}x}

Por tanto, concluimos que la respuesta correcta es el inciso a).

Reactivo 19

¿Para qué valores de \alpha  , el coseno se anula?

1. 0
2. \frac{\pi }{2}+2\pi n
3. \frac{\pi }{2}+n\pi
4. Indeterminado

Solución:

En el primer cuadrante, el coseno se anula para \alpha =90°=\frac{\pi }{2} . Debido a que es una función cíclica, cada 180°=\pi  \mathrm{r}\mathrm{a}\mathrm{d} respecto a \pi /2 el coseno se anulará. Para generalizar esto, podemos expresar los infinitos puntos en los que se anula el coseno como:

\alpha =\frac{\pi }{2}+n\pi  \forall  n\ge 0

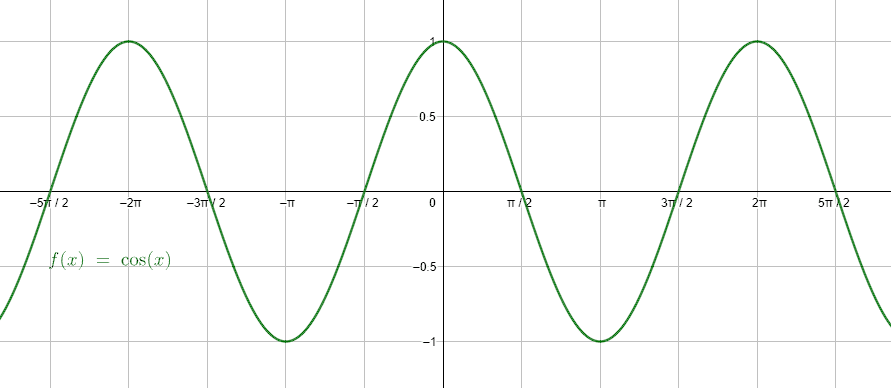
La respuesta correcta es el inciso c).

Reactivo 20

¿Cuántas diagonales se pueden trazar en un decágono?

1. \frac{n\left(n-3\right)}{3}
2. \frac{n\left(n-3\right)}{2}
3. \frac{n\left(n-1\right)}{2}
4. \frac{n\left(n+3\right)}{2}

Solución:

Primero, debemos recordar que un decágono es un polígono de 9 lados y 9 vértices. Por otra parte, tenemos la siguiente ecuación que nos permite calcular el número de aristas que interconectan a todos los vértices de un polígono.

A=\frac{n\left(n-1\right)}{2}

Si a esta expresión le restamos el número de vértices, es decir, n nos queda:

D=A-n=\frac{n\left(n-1\right)}{2}-n=\frac{n\left(n-1\right)-2n}{2}=\frac{n\left(n-3\right)}{2}

Las diagonales en un polígono pueden calcularse con la expresión:

D=\frac{n\left(n-3\right)}{2}

La respuesta correcta es el inciso b).