Hola de nuevo aspirante, vamos con la solución de la cuarta parte del examen simulacro de pensamiento matemático del Exani II, en esta parte resolveremos los ejercicios del 31 al 40.

Hasta el momento hemos resuelto 30 de los 50 reactivos del examen, ¿Cómo te ha ido? Es normal equivocarse aquí, ¿O prefieres equivocarte en el examen real?, Sigue estudiando y lograrás tu meta de entrar a la universidad.
Reactivo 31
A partir de la gráfica de la parábola que se muestra a continuación, determine su ecuación.
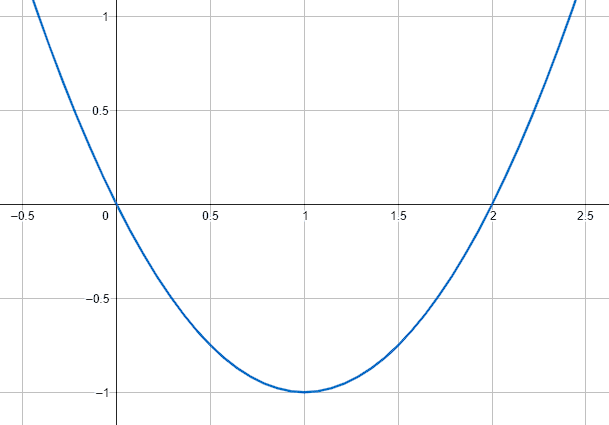
- y={x}^{2}-2x+1
- y={x}^{2}+2x
- y={x}^{2}-2x
Solución:
Para encontrar la ecuación de la parábola que abre de forma vertical, empleamos la siguiente forma ordinaria.
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Donde \left(h, k\right) son las coordenadas del centro y 4p el lado recto. Las coordenadas del centro se extraen por inspección de la gráfica.
\left(h, k\right)=\left(1, -1\right)
Sustituimos en la ecuación ordinaria.
{\left(x-1\right)}^{2}=4p\left(y+1\right)
Para determinar el valor de 4p sustituimos cualquier punto que pertenezca a la parábola. Examinando la gráfica, empleamos el \left(0, 0\right) .
1=4p
Finalmente:
{\left(x-1\right)}^{2}=y+1\to {x}^{2}-2x+1=y+1
y={x}^{2}-2x
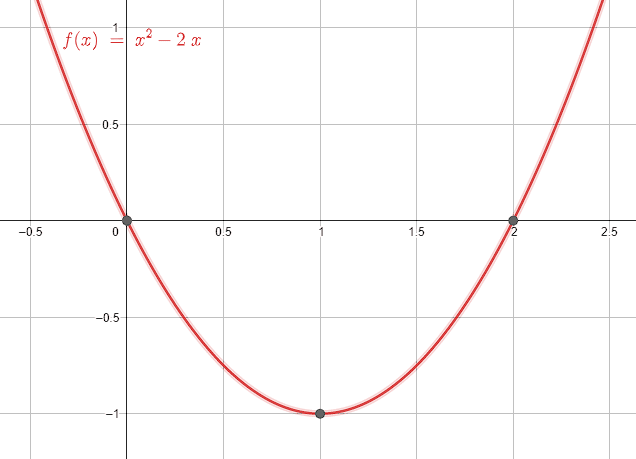
La respuesta correcta es el inciso c).
Reactivo 32
Una recta pasa por el punto P\left(1, 1\right) y es perpendicular a otra cuya ecuación es y=x+1 . Calcule la ecuación de la recta que pasa por el punto P .
- y=1-x
- y=2-x
- y=2+x
Solución:
Para calcular la ecuación de la recta que solicita el enunciado, debemos emplear la siguiente relación de pendientes entre rectas que son perpendiculares.
{m}_{2}=-\frac{1}{{m}_{1}}
Examinando la ecuación y=x+1 , determinamos que {m}_{1}=1 .
{m}_{2}=-\frac{1}{1}=-1
Ahora, sustituimos la pendiente y el punto en la ecuación punto-pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)
y-1=-\left(x-1\right)\to y=1-x+1
y=2-x
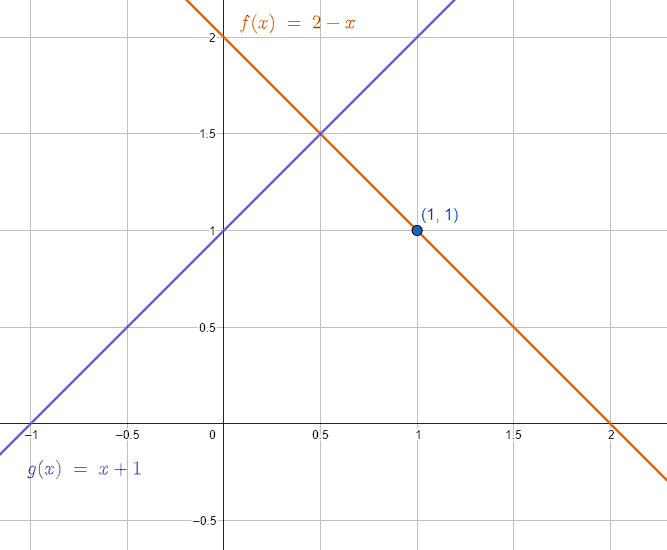
Concluimos que la respuesta correcta es el inciso b).
Reactivo 33
¿Cuál es la ecuación de la circunferencia con centro en el punto \left(1, 1\right) y que pasa por el punto A\left(1, 2\right) ?
- {\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}=1
- {\left(x+1\right)}^{2}+{\left(y+1\right)}^{2}=1
- {\left(x-1\right)}^{2}+{\left(y+1\right)}^{2}=1
Solución:
Iniciamos escribiendo la ecuación ordinaria de la circunferencia.
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
Donde: \left(h, k\right)=\left(1, 1\right) y el radio es desconocido.
Si recordamos la definición del lugar geométrico de una circunferencia, la distancia entre cualquier punto de la circunferencia y su centro es constante y vale r . Por tanto, podemos calcular a r como la distancia d\left(C, A\right) .
r=\sqrt{{\left(1-1\right)}^{2}+{\left(2-1\right)}^{2}}=1
Sustituimos todo en la ecuación de la circunferencia:
{\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}=1
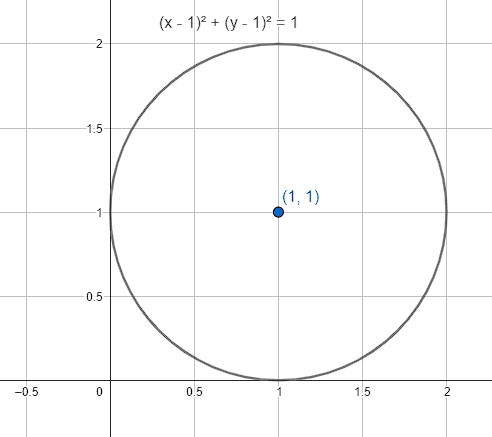
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 34
A partir de la siguiente fracción algebraica, determine su descomposición en fracciones parciales.
\frac{1}{x\left(x-3\right)\left({x}^{2}+x+1\right)}
- -\frac{1}{3x}+\frac{1}{39\left(x-3\right)}+\frac{4x+3}{13\left({x}^{2}+x+1\right)}
- -\frac{1}{3x}+\frac{1}{9\left(x-3\right)}-\frac{4x+3}{13\left({x}^{2}+x+1\right)}
- -\frac{1}{3x}+\frac{1}{39\left(x-3\right)}+\frac{4x}{13\left({x}^{2}+x+1\right)}
Solución:
Para encontrar la descomposición en fracciones parciales, debemos identificar el tipo de factores que hay en el denominador.
Tenemos a dos factores lineales: x y x-3 , junto a un factor primo de segundo grado {x}^{2}+x+1 . Para los dos primeros, el numerador de la fracción parcial es una constante {a}_{1} y {a}_{2} , mientras que para el tercero es un binomio lineal {a}_{3}x+{a}_{4} .
\frac{1}{x\left(x-3\right)\left({x}^{2}+x+1\right)}=\frac{{a}_{1}}{x}+\frac{{a}_{2}}{x-3}+\frac{{a}_{3}x+{a}_{4}}{{x}^{2}+x+1}
Pasamos a multiplicar el numerador de la izquierda a la derecha.
1={a}_{1}\left(x-3\right)\left({x}^{2}+x+1\right)+{a}_{2}x\left({x}^{2}+x+1\right)+x\left({a}_{3}x+{a}_{4}\right)\left(x-3\right)
Desarrollamos todos los productos.
1={a}_{1}\left({x}^{3}-2{x}^{2}-2x-3\right)+{a}_{2}\left({x}^{3}+{x}^{2}+x\right)+{a}_{3}{x}^{3}+\left({a}_{4}-3{a}_{3}\right){x}^{2}-3{a}_{4}x
Ahora, agrupamos términos semejantes.
1=\left({a}_{1}+{a}_{2}+{a}_{3}\right){x}^{3}+\left(-2{a}_{1}+{a}_{2}+{a}_{4}-3{a}_{3}\right){x}^{2}+\left(-2{a}_{1}+{a}_{2}-3{a}_{4}\right)x-3{a}_{1}
Aplicamos igualación de coeficientes.
\left\{\begin{array}{c}\begin{array}{c}{a}_{1}+{a}_{2}+{a}_{3}=0\\ -2{a}_{1}+{a}_{2}-3{a}_{3}+{a}_{4}=0\end{array}\\ \begin{array}{c}-2{a}_{1}+{a}_{2}-3{a}_{4}=0\\ -3{a}_{1}=1\end{array}\end{array}\right.
De la cuarta ecuación, despejamos el valor de {a}_{1} .
{a}_{1}=-\frac{1}{3}
Sustituimos este valor en el resto de ecuaciones.
\left\{\begin{array}{c}-\frac{1}{3}+{a}_{2}+{a}_{3}=0\to {a}_{2}+{a}_{3}=\frac{1}{3}\\ \frac{2}{3}+{a}_{2}-3{a}_{3}+{a}_{4}=0\to {a}_{2}-3{a}_{3}+{a}_{4}=-\frac{2}{3}\\ \frac{2}{3}+{a}_{2}-3{a}_{4}=0\to {a}_{2}-3{a}_{4}=-\frac{2}{3}\end{array}\right.
No vamos a expandir la solución del sistema de ecuaciones lineales, debido a que excede la finalidad del ejercicio. Aclarado esto:
\begin{array}{c}{a}_{2}=\frac{1}{39}\\ {a}_{3}=\frac{4}{13}\\ {a}_{4}=\frac{3}{13}\end{array}
Sustituimos los coeficientes en la descomposición.
\frac{1}{x\left(x-3\right)\left({x}^{2}+x+1\right)}=-\frac{1}{3x}+\frac{1}{39\left(x-3\right)}+\frac{4x+3}{13\left({x}^{2}+x+1\right)}
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 35
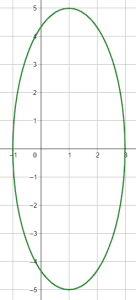
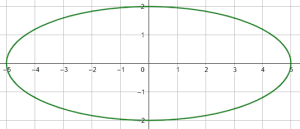
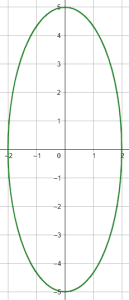
Indique la gráfica que corresponde con la elipse representada por la ecuación \frac{{x}^{2}}{4}+\frac{{y}^{2}}{25}=1 .
Solución:
En este caso, debemos identificar 3 aspectos en la ecuación de la elipse: la orientación, el centro y la longitud de los semiejes.
La orientación se refiere a si la elipse es vertical u horizontal. Será horizontal si el semieje mayor es el denominador de la x o, será vertical si es denominador de la y . En la ecuación del enunciado, el denominador mayor lo tiene la y , por tanto: es una elipse vertical.
Ahora, el centro de la elipse es el origen, porque tanto h como k son nulos. Por último, la longitud de los semiejes es:
a=\sqrt{25}=5
b=\sqrt{4}=2
Con toda esta información y examinando a los incisos, concluimos que la respuesta correcta es c).
Reactivo 36
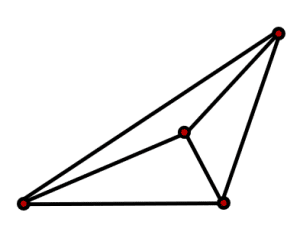
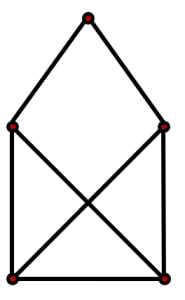
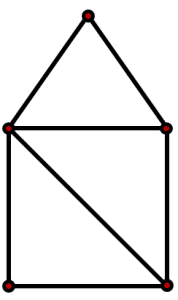
¿Cuál de las siguientes figuras se puede recorrer sin levantar el lápiz?
Solución:
Para resolver este tipo de problemas, debemos tener presente algunas reglas que nos dirán si la figura puede o no unirse con un solo trazo.
- Si los puntos de la figura son todos pares, entonces puede unirse con un mismo trazo
- Si hay un solo par de puntos impares, los vértices pueden unirse con un solo trazo
- Si hay más de dos puntos impares, la figura no podrá unirse con un solo trazo
Teniendo esto presente, solo nos queda estudiar el número de aristas que llegan a cada punto.
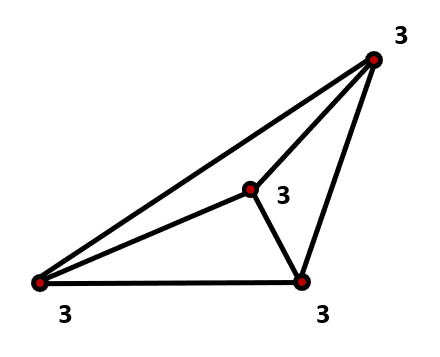
La figura a) tiene 4 puntos impares. No puede unirse con un mismo trazo.
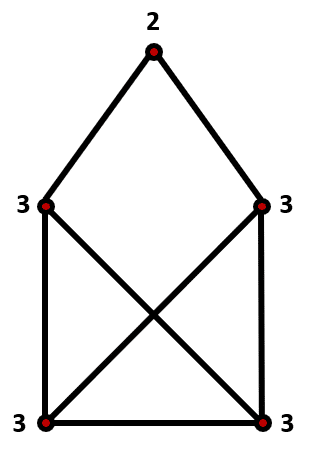
La figura b) tiene 4 puntos impares y uno par. No puede unirse con un solo trazo.
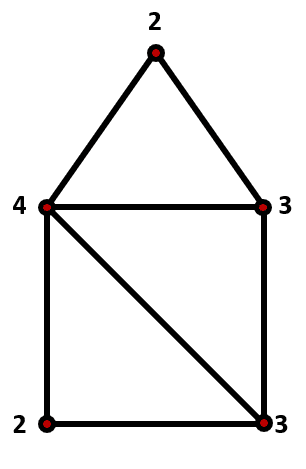
La figura c) tiene solo 2 puntos impares. Puede unirse con un mismo trazo iniciando en uno de los puntos impares, terminando el recorrido en el otro. La respuesta correcta es el inciso c).
Reactivo 37
Es el resultado de la expresión
3\left(4+5\right)+\frac{3}{2}\left(5-3\right)-\sqrt{2\left(6-4\right)}
- 28
- 27
- 32
Solución:
En este caso, debemos seguir las reglas de jerarquía de operaciones para encontrar el resultado correcto. El orden para resolver operaciones aritméticas, manteniendo el sentido de izquierda a derecha, es:
- Llaves, corchetes y paréntesis
- Potencias y radicales
- Multiplicaciones y divisiones
- Sumas y restas
Teniendo esto en mente, iniciamos por resolver los paréntesis.
3\left(4+5\right)+\frac{3}{2}\left(5-3\right)-\sqrt{2\left(6-4\right)}=3\left(9\right)+\frac{3}{2}\left(2\right)-\sqrt{2\left(2\right)}
Deshacemos los productos indicados con paréntesis.
3\left(9\right)+\frac{3}{2}\left(2\right)-\sqrt{2\left(2\right)}=27+3-\sqrt{4}
Resolvemos la raíz cuadrada y luego las sumas y restas.
27+3-\sqrt{4}=27+3-2=28
Finalmente:
3\left(4+5\right)+\frac{3}{2}\left(5-3\right)-\sqrt{2\left(6-4\right)}=28
Concluimos el problema indicando como respuesta correcta al inciso a).
Reactivo 38
Una empresa de encomiendas necesita de 4 hombres para descargar 250 paquetes en 5 horas. Debido al black friday, estiman que los paquetes aumentarán a 560 para esas fechas. ¿Cuántos hombres necesitan para descargar todo en 8 horas?
- 4
- 6
- 3
Solución:
En este caso, debemos emplear una regla de tres compuesta, debido a que tenemos 3 variables: cantidad de hombres, número de paquetes y tiempo en horas. Reacomodamos los datos en una tabla.

Ahora, debemos establecer las relaciones entre nuestra incógnita y el resto de variables.
Tiempo – Número de hombres: a mayor número de hombres, menor será el tiempo de trabajo. Relación inversa.
Paquetes – Número de hombres: a mayor número de paquetes, más hombres se necesitan para el trabajo. Relación directa.
La regla de tres compuesta quedaría como:
\frac{x}{4}=\left(\frac{5}{8}\right)\left(\frac{560}{250}\right)\to x=\frac{28}{5}=5.6
Aproximando por exceso, concluimos que se necesitan 6 hombres para cumplir con el trabajo.
La respuesta correcta es el inciso b).
Todas las partes del Simulacro:
Reactivo 39
Se tiene un triángulo acutángulo, del que se conocen los 2 lados y 1 ángulo, tal como se muestra en la figura.
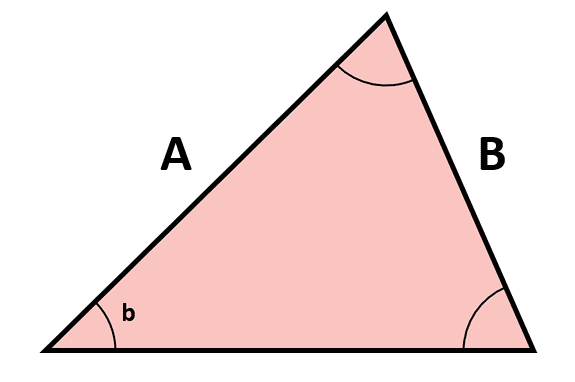
¿Cuál de las leyes de los triángulos se debe utilizar para encontrar el ángulo opuesto al lado A ?
- Ley de Senos
- Teorema de Tales
- Ley de Cosenos
Solución:
De los temas relacionados a la trigonometría, sabemos que los triángulos acutángulos y obtusángulos no se pueden resolver mediante el teorema de Pitágoras (por lo menos, no de forma directa).
En estos casos, tenemos otras dos herramientas: la ley del seno y la ley del coseno. Para aplicar la ley de los senos, necesitamos conocer al menos 2 ángulos y un lado o, 2 lados y un ángulo.
Por otra parte, para la ley de los cosenos debemos conocer 2 lados y el ángulo opuesto al lado desconocido o, a los tres lados.
La ley del coseno no se puede aplicar de forma directa, porque no conocemos al lado C . Tendríamos que aplicar primero respecto de B , calcular a C y luego proceder con el ángulo a . En contraparte, la ley del seno nos permite encontrar al ángulo a de forma inmediata.
\frac{A}{\mathrm{sin}a}=\frac{B}{\mathrm{sin}b}
Concluimos el ejercicio indicando como respuesta correcta al inciso a).
Reactivo 40
Un servidor tiene problemas para gestionar el tráfico de los usuarios en horas pico. Este ha sido diseñado para responder 10000 solicitudes en 20 segundos con 16 Gb de memoria RAM. En las horas álgidas, las solicitudes incrementan a 25000 y deben ser atendidas en 25 segundos. ¿Cuánta memoria debe adicionarse al servidor para que cumpla con el trabajo?
- 16
- 32
- 8
Solución:
Para resolver el problema que plantea el enunciado, debemos emplear una regla de tres compuesta. Debe ser compuesta, porque hay 3 variables en juego: solicitudes, tiempo y memoria RAM.
Ordenamos los datos en una tabla.

La relación entre las solicitudes y la cantidad de RAM es lineal ya que, con mayor cantidad de RAM se pueden manejar más solicitudes. Por otra parte, al tener más memoria RAM el tiempo de ejecución disminuye, por tanto, la relación es directa.
La regla de tres quedaría como:
\frac{x}{16}=\left(\frac{25000}{10000}\right)\left(\frac{20}{25}\right)\to x=16\left(\frac{25000}{10000}\right)\left(\frac{20}{25}\right)
x=32 \mathrm{G}\mathrm{b}
Considerando los 16 Gb de RAM iniciales, se deben instalar otros 16 Gb para cumplir con los requerimientos. La respuesta correcta es el inciso a).