Hola, futuro universitario! ¿Listo para practicar el módulo de aritmética del EXANI II? Aquí te traemos los reactivos del 11 al 20 del examen simulador, para que sigas practicando y reforzando tus conocimientos en matemáticas.

Vamos a repasar temas que van desde desigualdades hasta operaciones con números enteros, asegurándonos de que no te tome por sorpresa ninguna pregunta en el examen real.
Estos ejercicios te ayudarán a familiarizarte con el tipo de problemas que podrías encontrar en el examen, y te permitirán identificar en qué áreas ya te sientes seguro y en cuáles necesitas trabajar un poco más. ¡Comencemos!
Temas que cubrimos en estos reactivos:
- Desigualdades
- Operaciones básicas con fracciones y números enteros
- Sumas y restas
- Proporciones
- Cálculos de gastos y presupuestos
- Comparación de precios
- Sistemas de ecuaciones simples
- Autonomía de combustible
- Operaciones con potencias
- Resolución de problemas cotidianos
Vamos a resolverlos juntos y a prepararnos lo mejor posible para el examen.
Reactivo 11
Dada la siguiente desigualdad, resuelva las operaciones indicadas y diga si se cumple o no la desigualdad final.
{2}^{2}-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+{2}^{2}-3
- La desigualdad es cierta
- La desigualdad es falsa
- Se trata de una igualdad
Solución:
Las desigualdades nos permiten expresar relaciones entre cantidades numéricas más allá de que puedan ser iguales. Primero, es necesario resolver las operaciones indicadas en ambos miembros. Iniciamos calculando las potencias.
{2}^{2}-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+{2}^{2}-3\to 4-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+4-3
Ahora, vamos con las sumas y restas respectivamente.
4-\frac{3}{4}+\frac{1}{4}>\frac{3}{2}+4-3\to \frac{13}{4}+\frac{1}{4}>\frac{11}{2}-3
\frac{13}{4}+\frac{1}{4}>\frac{11}{2}-3\to \frac{7}{2}>\frac{5}{2}
Multiplicamos ambos miembros por 2. El sentido de la desigualdad se mantiene porque el factor es positivo.
2\cdot \frac{7}{2}>2\cdot \frac{5}{2}\to 7>5
La desigualdad es cierta, el número 7 es mayor que el número 5.
Indicamos como respuesta correcta al inciso a).
Reactivo 12
Joaquín es un estudiante universitario que está calculando cuánto dinero gasta al mes. Las últimas facturas indican que pagó 560$ en alquiler, 400$ en comida, 180$ para desplazarse a la universidad y 590$ en gastos varios. ¿Cuánto dinero necesita Joaquín mensualmente?
- Menos de 1700$
- Al menos 1730$
- Más de 200$
Solución:
La suma de todos los gastos de Joaquín en un mes es:
560+400+180+590=1730 \mathrm{\$}
Entonces, Joaquín necesita por lo menos 1730$ al mes.
La respuesta correcta es el inciso b).
Reactivo 13
Un auto de segunda mano, pero en excelentes condiciones cuesta 100,000$, mientras que uno totalmente nuevo 20,000$ más que el de segunda mano. Si un coche del mismo modelo, pero del año cuesta la semisuma de los coches anteriores, ¿cuánto se debería pagar por este último?
- 110,000$
- 220,000$
- 120,000$
Solución:
Iniciemos estableciendo el costo de los dos primeros coches.
{\mathrm{C}}_{\mathrm{s}\mathrm{m}}=100000\$
{\mathrm{C}}_{\mathrm{n}}={\mathrm{C}}_{\mathrm{s}\mathrm{m}}+20000\$=100000\$+20000\$=120000\$
Ahora, el costo del tercer coche se obtiene mediante la semisuma de los costos anteriores. La semisuma de dos cantidades, es igual a la suma de las cantidades divididas entre 2.
{\mathrm{C}}_{\mathrm{a}\mathrm{ñ}\mathrm{o}}=\frac{{\mathrm{C}}_{\mathrm{s}\mathrm{m}}+{\mathrm{C}}_{\mathrm{n}}}{2}=\frac{100000+120000}{2}=\frac{220000}{2}=110000\$
El coche del año actual tiene un costo de 110,000$ pesos.
La respuesta correcta es el inciso a).
Reactivo 14
Un usuario abona a su cuenta bancaria 50,000$ como concepto de ahorros. Pasada una semana retira 25,000$ y dos días después paga una cuenta de 9,000$. Al final del mes abona 20,000$ más. ¿Cuál es el balance de la cuenta bancaria?
- 34,000$
- 25,000$
- 36,000$
Solución:
Para encontrar el saldo final, debemos ir sumando y restando los ingresos y egresos respectivamente. Al inicio del mes, el usuario tiene un balance de 50,000$.
{\mathrm{S}}_{1}=\mathrm{50,000}
Luego hace un retiro de 25,000$ pesos.
{\mathrm{S}}_{2}=\mathrm{50,000}-\mathrm{25,000}=\mathrm{25,000}
Dos días después hace un pago, esto cuenta como egreso.
{\mathrm{S}}_{3}=\mathrm{25,000}-\mathrm{9,000}=\mathrm{16,000}\$
Finalmente, el usuario ingresa 20,000$.
{\mathrm{S}}_{4}=\mathrm{16,000}+\mathrm{20,000}=\mathrm{36,000}\$
El saldo final es de 36,000 pesos.
Indicamos como respuesta correcta al inciso c).
Reactivo 15
José ha iniciado un nuevo emprendimiento y, como buen comerciante, estaba revisando las finanzas de la última semana. Se dio cuenta que el lunes ganó 2,500$ y que existe una proporción de 4/3 entre dos días consecutivos: día actual entre día anterior. ¿Cuánto dinero ganaría José de su negocio si trabaja 6 días a la semana?
- 30,640$
- 35,640$
- 34,640$
Solución:
El enunciado indica que José ganó 2,500 pesos y que existen una razón entre lo ganado el día actual y el día siguiente de 4/3, es decir:
\frac{{\mathrm{D}}_{\mathrm{a}\mathrm{c}}}{{\mathrm{D}}_{\mathrm{a}\mathrm{n}}}=\frac{4}{3}\to {\mathrm{D}}_{\mathrm{a}\mathrm{c}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{a}\mathrm{n}}
Esto quiere decir que, estando en el martes la ganancia será 4/3 multiplicado por la ganancia del lunes. La del miércoles 4/3 por la ganancia del martes y así sucesivamente hasta llegar al sábado, sexto día de la semana que labora José.
Ganancia del lunes.
{\mathrm{D}}_{\mathrm{L}}=2500
Ganancia del martes.
{\mathrm{D}}_{\mathrm{M}\mathrm{a}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{L}}=3333.3
Ganancia del miércoles.
{\mathrm{D}}_{\mathrm{M}\mathrm{i}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{M}\mathrm{a}}=4444.4
Ganancia del jueves.
{\mathrm{D}}_{\mathrm{J}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{M}\mathrm{i}}=5926
Ganancia del viernes.
{\mathrm{D}}_{\mathrm{V}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{J}}=7901.2
Ganancia del sábado.
{\mathrm{D}}_{\mathrm{S}}=\frac{4}{3}{\mathrm{D}}_{\mathrm{V}}=10535
La ganancia de toda la semana es la suma del ingreso por los 6 días hábiles.
\mathrm{G}=2500+3333.3+4444.4+5926+7901.2+10535=34639.9
Finalmente:
\mathrm{G}=\mathrm{34,640}\mathrm{\$}
La respuesta correcta es el inciso c).
Reactivo 16
Dada la siguiente cuadrícula con algunos rectángulos colocados de manera irregular, indique cuál de las opciones permite obtener el total de los rectángulos sin contar uno a uno.
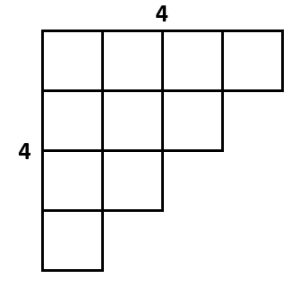
- 4\times 4
- 4\times 4-2\times 2-2
- 4\times 4-2-1
Solución:
Debemos encontrar una expresión aritmética que nos permita calcular el total de casillas que conforman a la cuadrícula. Iniciamos indicando que, si estuviese completa, el total sería 4\times 4 .
Dibujando sobre la figura, estas son las casillas faltantes.
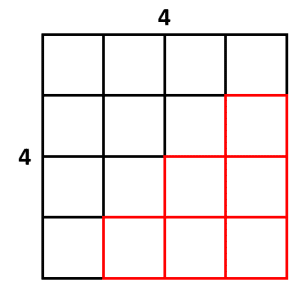
Vemos que se forma una cuadrícula de 2\times 2 junto a otros dos rectángulos uno en la parte superior y otro a la izquierda en la zona inferior. Debemos restar 2\times 2+2 a la cuadrícula completa para obtener el total de cuadros negros.
\mathrm{C}\mathrm{u}\mathrm{a}\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}=4\times 4-2\times 2-2
La respuesta correcta es el inciso b).
Reactivo 17
Esteban va a una papelería para comprar algunas libretas y lápices, los cuales tienen un precio de 15$ y 5$ respectivamente. Al llegar a la caja, se da cuenta que el total fue de 120$, si Esteban compró la misma cantidad de libretas que de lápices, ¿cuánto llevó de cada una?
- Llevó 6 de cada una
- Llevó 5 de cada una
- Llevó 7 de cada una
Solución:
Lo primero que podemos extraer del enunciado, es el precio unitario de las libretas y los lápices.
{\mathrm{P}}_{\mathrm{L}\mathrm{a}}=5\$
{\mathrm{P}}_{\mathrm{L}\mathrm{i}}=15\$
Llamaremos al total de lápices como \mathrm{L}\mathrm{a} y al total de libretas \mathrm{L}\mathrm{i} . El costo total a pagar es igual al total de lapiceros por su precio más, el total de libretas por su precio.
120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{i}
Por otra parte, Esteban llevó la misma cantidad de lápices que de libretas.
\mathrm{L}\mathrm{a}=\mathrm{L}\mathrm{i}
Dejamos a la expresión anterior con solo \mathrm{L}\mathrm{a} .
120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{i}\to 120=5\mathrm{L}\mathrm{a}+15\mathrm{L}\mathrm{a}\to 120=20\mathrm{L}\mathrm{a}
Despejamos:
\mathrm{L}\mathrm{a}=\frac{120}{20}=6\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{p}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{s}
Debido a que \mathrm{L}\mathrm{a}=\mathrm{L}\mathrm{i} :
\mathrm{L}\mathrm{i}=6\mathrm{ }\mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{s}
Estaban llevando 6 libretas y 6 lapiceros de la tienda.
La respuesta correcta es el inciso a).
Reactivo 18
Se sabe que un ordenador gaming cuesta el doble que un ordenador de oficina básico. ¿Cuál de las siguientes comparaciones es correcta?
- El precio del ordenador gaming es igual a la mitad del precio del ordenador de oficina
- El precio del ordenador de oficina es mayor que la mitad del precio del ordenador gaming
- La cuarta parte del precio del ordenador gaming es menor el precio del ordenador de oficina
Solución:
Para resolver el problema, expresamos a la relación de precios entre los computadores como una razón.
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2
De esta razón obtenemos dos igualdades equivalentes:
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2\to {\mathrm{P}}_{\mathrm{g}}=2{\mathrm{P}}_{\mathrm{o}}
El precio del ordenador gaming es el doble que el de oficina.
\frac{{\mathrm{P}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{o}}}=2\to {\mathrm{P}}_{\mathrm{o}}=\frac{1}{2}{\mathrm{P}}_{\mathrm{g}}
El precio del ordenador de oficina es la mitad que el gaming.
Las dos primeras aseveraciones son falsas. Porque el precio del ordenador de oficina no es mayor (en ninguna proporción) al ordenador gaming. Por descartes, la respuesta correcta es el inciso c).
Reactivo 19
La suma de dos cantidades enteras es 1300 y su resta es igual a 300. ¿Cuál es el valor de dichas cantidades?
- 1000 y 200
- 300 y 1000
- 500 y 800
Solución:
Debemos expresar las relaciones en lenguaje matemático. Llamaremos a las cantidades x y y .
La suma de dos cantidades enteras es 1300…
x+y=1300
…su resta es igual a 300.
x-y=300
Despejamos a x .
x=y+300
Sustituimos en la primera expresión.
y+300+y=1300\to 2y=1000
\therefore y=500
Finalmente:
x=500+300=800
Las cantidades enteras son 500 y 800.
La respuesta correcta es el inciso c).
Reactivo 20
Un automóvil tiene una autonomía del combustible de 2 kilómetros por litro. Si el conductor necesita realizar un viaje de 150 kilómetros ¿Cuántos litros de combustible extra debe llevar con él si el tanque tiene capacidad máxima de 40 litros?
- 20 litros extra
- 30 litros extra
- 35 litros extra
Solución:
La autonomía de combustible del automóvil la podemos expresar como la razón:
\mathrm{A}=\frac{2\mathrm{ }\mathrm{k}\mathrm{m}}{1 \mathrm{L}}=2\frac{\mathrm{k}\mathrm{m}}{\mathrm{L}}
Ahora, dividimos los 150 kilómetros del viaje para obtener el total de combustible.
\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}=\frac{150}{2}=75 \mathrm{L}\mathrm{i}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
Si el tanque tiene 40 litros, el conductor deberá llevar consigo al menos otros 35 litros de combustible para cubrir el viaje. La respuesta correcta es el inciso c).
Simulacro Guía EXANI-II Módulo Aritmética 50 reactivos

