¡Hola aspirante! En este tutorial resolveremos la primera parte del examen simulacro de la Guía EXANI II para el módulo de Aritmética. Iniciamos desde el reactivo 1 hasta el 10.

Resuelve los problemas por tu cuenta antes de checar la solución. Es importante que desarrolles tu capacidad de análisis y solución de problemas antes del examen.
Estructura del EXANI II
La prueba de ingreso EXANI II, consta de dos partes: habilidades y conocimientos y los módulos específicos. Algunas universidades aplican una prueba diagnóstico de inglés, la cual no cuenta para aprobar el examen.
Examen de habilidades y conocimientos
La primera parte del examen se aplica para todas las carreras y tiene una extensión de 90 reactivos: 60 de Español y 30 de Matemáticas. La siguiente tabla resume la distribución de los reactivos en la prueba:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Por otro lado, en la segunda parte los estudiantes deben responder 2 módulos específicos, que varían de acuerdo a la carrera. Debes revisar la convocatoria de tu universidad para conocer cuáles de los 15 módulos debes estudiar.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Aritmética EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de aritmética, con el temario desglosado que va para el examen.
| Subárea | Reactivos |
|---|---|
| Principios de números reales | 14 |
| Problemas con números reales | 10 |
| Total | 24 |
Subárea: Principios de números reales
- Operaciones básicas con números enteros, fracciones y decimales
- Ley de los signos
- Potenciación
- Signos de agrupación
- Expresiones algebraicas con radicales
- Notación científica
- Factores primos
- Reglas de divisibilidad
- Mínimo común múltiplo
- Máximo común divisor
Subárea: Problemas con números racionales
- Razón y proporción
- Porcentaje
- Progresión geométrica
- Progresión aritmética
- Reparto proporcional
- Interés simple
- Regla de tres
Recomendaciones para resolver la guía interactiva
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Para la operación aritmética que se muestra a continuación, ¿qué ley de signos debería aplicarse?
\left(-a\right)\left(b\right)
- La ley de los signos para la suma
- La ley de los signos para la división
- La ley de los signos para el producto
Solución:
Debido a que encerrar a los operandos entre paréntesis sin colocar ningún signo de suma, resta o división entre ellos, indica que se deben multiplicar; la ley de signos que debe aplicarse es la del producto.
Como a es negativo y b positivo, el resultado de multiplicarlos será negativo teniendo en cuenta dicha ley de signos. La respuesta correcta es el inciso c).
Reactivo 2
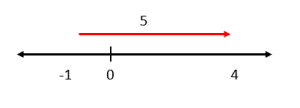
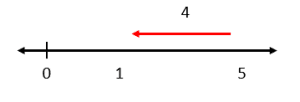
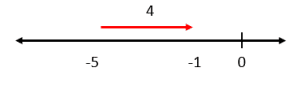
Dada la siguiente operación aritmética, seleccione la imagen que posiciona correctamente los operandos y el resultado sobre la recta real.
4-5=-1
Solución:
Sobre la recta real, la suma y la resta pueden expresarse como desplazamientos a la derecha o hacia la izquierda respectivamente. Para la resta del enunciado, tomamos al primer operando: 4, y nos desplazamos hacia la izquierda 5 posiciones.
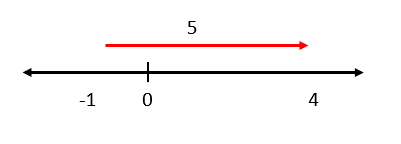
Examinando a los incisos, vemos que ninguno corresponde con la solución. Valiéndonos de la propiedad conmutativa de la suma, cambiamos de lugar al 4 y -5.
4-5=-1\to -5+4=-1
Esto significa pararnos en -5 y desplazarnos 4 posiciones hacia la derecha.
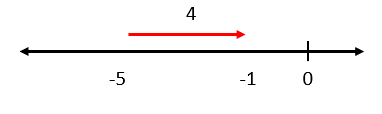
Comparando con los incisos, la respuesta correcta es c).
Reactivo 3
Resuelva la siguiente operación aritmética aplicando correctamente las leyes de los signos.
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]
- \frac{4}{5}
- 3
- 4
Solución:
Para resolver el problema, debemos recordar las reglas de jerarquía de operaciones y signos de agrupación. El orden de solución es:
- Llaves
- Corchetes
- Paréntesis
- Potencias y raíces
- Productos y cocientes
- Sumas y restas
La importancia disminuye a medida que bajamos en la lista. Teniendo esto en cuenta, debemos resolver primero el interior de los corchetes.
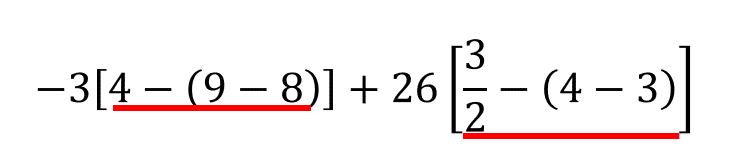
Ahora, dentro de los corchetes aplicando la jerarquía de operaciones, determinamos que hay que resolver el interior de los paréntesis.
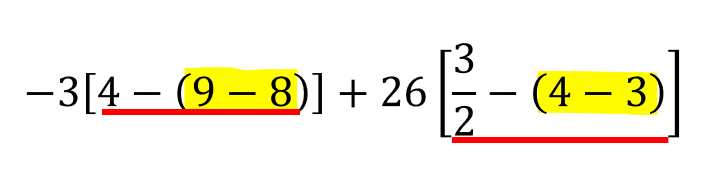
Resolviendo:
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]=-3\left[4-\left(1\right)\right]+26\left[\frac{3}{2}-\left(1\right)\right]
Eliminamos los paréntesis multiplicando el signo externo por el número.
-3\left[4-\left(1\right)\right]+26\left[\frac{3}{2}-\left(1\right)\right]=-3\left[4-1\right]+26\left[\frac{3}{2}-1\right]
Resolvemos lo que queda en el interior de los corchetes.
-3\left[4-1\right]+26\left[\frac{3}{2}-1\right]=-3\left[3\right]+26\left[\frac{1}{2}\right]
Deshacemos los corchetes resolviendo los productos indicados.
-3\left[3\right]+26\left[\frac{1}{2}\right]=-9+13
Finalmente, restamos.
-9+13=4
-3\left[4-\left(9-8\right)\right]+26\left[\frac{3}{2}-\left(4-3\right)\right]=4
La respuesta correcta es el inciso c).
Reactivo 4
Identifique la frase que ejemplifica la aplicación de la radicación a una cantidad.
- El promedio académico de un estudiante, es igual a la suma de sus calificaciones dividida por el número de evaluaciones
- El área de un cuadrado es igual a la segunda potencia de su lado
- La hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de la suma de sus catetos
Solución:
Analizando las frases de los incisos, tenemos que tanto a) como b) establecen sumas, divisiones y productos, pero no hay ninguna raíz cuadrada. Por otra parte, el inciso c) indica de manera explícita una raíz cuadrada.
La hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de la suma de sus catetos.
h=\sqrt{{c}_{1}^{2}+{c}_{2}^{2}}
La respuesta correcta es el inciso c).
Reactivo 5
Dadas las fracciones {f}_{1}=\frac{22}{7} y {f}_{2}=\frac{14}{11} calcule: la suma, la resta {f}_{1}-{f}_{2} y el producto.
- \frac{340}{77}, \frac{144}{77}, 4
- 4, \frac{344}{77}, \frac{144}{77}
- \frac{144}{77}, \frac{344}{77}, 4
Solución:
Iniciamos calculando la suma de las fracciones.
\frac{22}{7}+\frac{14}{11}
Aplicamos el procedimiento para fracciones con distinto denominador.
\frac{22}{7}+\frac{14}{11}=\frac{\left(22\right)\left(11\right)+\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}
Resolvemos los productos.
\frac{\left(22\right)\left(11\right)+\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{242+98}{77}=\frac{340}{77}
Ahora, resolvemos la resta.
{f}_{1}-{f}_{2}=\frac{22}{7}-\frac{14}{11}
Operamos de la misma forma que con la suma, pero cambiando el signo “+” por un “-”.
\frac{22}{7}-\frac{14}{11}=\frac{\left(22\right)\left(11\right)-\left(7\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{242-98}{77}=\frac{144}{77}
Finalmente, calculamos el producto. La fracción resultante se obtiene multiplicando los numeradores y denominadores respectivamente.
\frac{22}{7}\times \frac{14}{11}=\frac{\left(22\right)\left(14\right)}{\left(7\right)\left(11\right)}=\frac{308}{77}
Esta fracción puede reducirse.
\frac{308}{77}=4
Ordenando los tres resultados:
\frac{340}{77}, \frac{144}{77}, 4
La respuesta correcta es el inciso a).
Reactivo 6
Relacione correctamente las propiedades de los radicales en la columna izquierda con las igualdades en la columna derecha.

- 1c, 2b, 3a
- 1b, 2a, 3c
- 1a, 2b, 3c
Solución:
Para relacionar correctamente las propiedades de la izquierda con las operaciones de la derecha, es necesario conocer previamente dichas propiedades de los radicales.
Radical como exponente fraccionario.

1c.
Producto de radicales con igual índice.
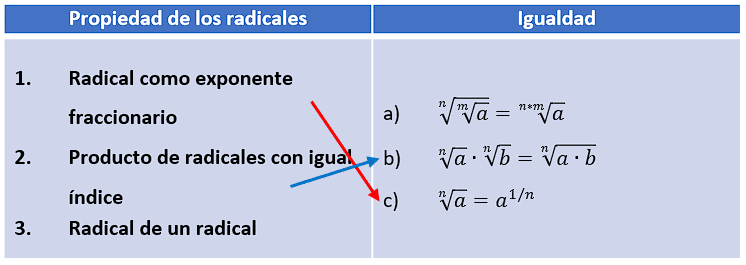
2b.
Por descartes: 3a. Uniendo todas las respuestas parciales: 1c, 2b, 3a.
La respuesta correcta es el inciso a).
Reactivo 7
Encuentre el resultado más simplificado de la siguiente expresión aritmética, aplicando las propiedades que sean necesarias.
\frac{{2}^{2}-{4}^{2}}{{3}^{2}-5}
- \frac{4}{5}
- -3
- \frac{1}{3}
Solución:
Siguiendo con las reglas de la jerarquía de operaciones, iniciamos resolviendo las potencias.
\frac{{2}^{2}-{4}^{2}}{{3}^{2}-5}=\frac{4-16}{9-5}
Resolvemos las operaciones en la fracción.
\frac{4-16}{9-5}=\frac{-12}{4}=-3
Indicamos como respuesta correcta al inciso b).
Reactivo 8
Transforma la fracción mixta 4\frac{1}{2} a fracción impropia.
- \frac{5}{2}
- \frac{9}{2}
- \frac{8}{2}
Solución:
La notación de las fracciones mixtas, permiten contraer la suma entre el número entero de la izquierda, con la fracción de la derecha.
4\frac{1}{2}=4+\frac{1}{2}
Es decir, la forma impropia se encuentra resolviendo esta suma.
4+\frac{1}{2}=\frac{\left(4\right)\left(2\right)+1}{2}=\frac{9}{2}
La respuesta correcta es el inciso b).
Reactivo 9
Calcule la siguiente expresión aritmética. Simplifique las fracciones mixtas para simplificar su resolución.
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}
- 5
- \frac{1}{5}
- 1
Solución:
Convertimos en fracciones impropias a las expresadas en forma mixta.
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}=\frac{4+\frac{1}{2}-4}{2+\frac{1}{2}}
Resolvemos la suma.
\frac{4+\frac{1}{2}-4}{2+\frac{1}{2}}=\frac{\frac{\left(4\right)\left(2\right)+1}{2}-4}{\frac{\left(2\right)\left(2\right)+1}{2}}=\frac{\frac{8+1}{2}-4}{\frac{4+1}{2}}=\frac{\frac{9}{2}-4}{\frac{5}{2}}
Ahora resolvemos la resta del numerador.
\frac{\frac{9}{2}-4}{\frac{5}{2}}=\frac{\frac{9-\left(2\right)\left(4\right)}{2}}{\frac{5}{2}}=\frac{\frac{9-8}{2}}{\frac{5}{2}}=\frac{\frac{1}{2}}{\frac{5}{2}}
Simplificamos el cociente de fracciones.
\frac{\frac{1}{2}}{\frac{5}{2}}=\frac{1}{2}÷\frac{5}{2}=\frac{\left(2\right)\left(1\right)}{\left(2\right)\left(5\right)}=\frac{1}{5}
Finalmente:
\frac{4\frac{1}{2}-4}{2\frac{1}{2}}=\frac{1}{5}
Indicamos como respuesta correcta al inciso b).
Reactivo 10
El encargado de una alberca escolar, ha notado que la misma se llena completamente en 2 horas. Si el volumen total de la alberca es de 1500 litros, ¿cuál es el valor de la razón en la que se llena la alberca en litros por minuto?
- 11 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
- 12 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
- 12.5 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
Solución:
El problema nos pide expresar mediante una razón, la rapidez con la que dicha alberca gana volumen de agua respecto del tiempo. Iniciamos convirtiendo las 2 horas a minutos.
Sabemos que 1 hora tiene 60 minutos.
2 \mathrm{h}\cdot \frac{60 \mathrm{m}\mathrm{i}\mathrm{n}}{1 \mathrm{h}}=120 \mathrm{m}\mathrm{i}\mathrm{n}
Dividimos ahora los 1500 litros entre los 120 minutos.
\frac{1500 \mathrm{L}}{120 \mathrm{m}\mathrm{i}\mathrm{n}}=12.5 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}
La alberca se llena a razón de 12.5 litros por minuto.
Indicamos como respuesta correcta al inciso c).