¿Cómo vas hasta el momento? Ahora vamos a resolver los reactivos del 31 al 40, ya casi terminamos, en este punto es importante que tomes nota de los ejercicios que más se te han complicado.

Vamos con la cuarta parte del examen simulador de álgebra, te recomiendo que midas el tiempo que te lleva resolverlos por tu cuenta.
Reactivo 31
Identificar el resultado al simplificar la siguiente expresión:
\sqrt{\left(x^{2}+11 x+17\right)-(x-8)}\left(-\sqrt{x^{2}}+\frac{8 y^{3}}{2 \sqrt[3]{y^{9}}}+\frac{\sqrt{y}}{y^{\frac{1}{2}}}\right)
- 5^{2}-x^{2}
- x^{2}-5^{2}
- x^{2}+5^{2}
- 5^{2}+x+x^{2}
Solución:
Para la expresión dentro de la raíz, deshacemos los paréntesis y resolvemos las sumas y restas. En el caso del otro factor, se aplican las correspondientes propiedades de los exponentes.
\sqrt{\left(x^{2}+11 x+17\right)-(x-8)}\left(-\sqrt{x^{2}}+\frac{8 y^{3}}{2 \sqrt[3]{y^{9}}}+\frac{\sqrt{y}}{y^{\frac{1}{2}}}\right)
\sqrt{x^{2}+11 x+17-x+8}(-x+4+1)
\sqrt{x^{2}+10 x+25}(5-x)
Aplicamos factorización al trinomio x^{2}+10 x+25 como trinomio cuadrado perfecto (a \pm b)^{2} , ya que cumple con la condición:
2 \sqrt{25 x^{2}}=10 x
2(5 x)=10 x
10 x=10 x
a=x \text{ y } b=5
x^{2}+10 x+25=(x+5)^{2}
Sustituyendo dentro de la raíz:
\sqrt{(x+5)^{2}}(5-x)=(5+x)(5-x)
Esto último se puede expresar como una diferencia de cuadrados:
(5+x)(5-x)=5^{2}-x^{2}
Conclusión, la respuesta correcta según las opciones dadas por el problema es la a).
Reactivo 32
Relacionar el método de factorización con la factorización adecuada del polinomio.

- 1C, 2A, 3D, 4B
- 1B, 2A, 3D, 4C
- 1B, 2D, 3A, 4C
- 1C, 2D, 3A, 4B
Solución:
Para determinar el método, procederemos a estudiar cada una de las expresiones de la columna derecha.
Polinomio A. 2 x^{2}-11 x+12
Por simple inspección, nos damos cuenta de que no puede ser un trinomio cuadrado perfecto, porque el primer término y el tercero no cumplen con la condición. Nos queda probar con trinomio de la forma a x^{2}+b x+c .
Multiplicamos la expresión por el coeficiente del término cuadrático
2\left(2 x^{2}-11 x+12\right)=4 x^{2}-11(2 x)+24
(2 x)^{2}-11(2 x)+24
Encontramos dos números que cumplan con la condición:
p_{1}+p_{2}=-11
p_{1} p_{2}=24
Estos números son:
p_{1}=-3 \text{ y } p_{2}=-8
Quedando factorizado como:
\frac{(2 x-3)(2 x-8)}{2}=\left(x-\frac{3}{2}\right)(x-4)
Entonces: A3.
Polinomio B. \frac{2}{4} x^{2} y-\frac{4}{3} y^{2} x
En este caso se presenta la factorización por monomio. No es posible aplicar diferencia de cuadrados y no es un trinomio. Trabajando la expresión se puede factorizar como:
\frac{2}{4} x^{2} y-\frac{4}{3} y^{2} x=x y\left(\frac{1}{2} x-\frac{4}{3} y\right)
Entonces: B4.
Polinomio C. 4 x^{2}-9 y^{2}
Si reacomodamos un poco el polinomio, nos queda una factorización por diferencia de cuadrados:
4 x^{2}-9 y^{2}=(2 x)^{2}-(3 y)^{2}=(2 x-3 y)(2 x+3 y)
Entonces: C1.
Polinomio D. 4 x^{2}-16 x+16
Es claro que la opción que queda es la de trinomio cuadrado perfecto, pero antes de afirmar cualquier cosa vamos a comprobarlo. Si el polinomio es trinomio cuadrado perfecto debe cumplirse que:
2 \sqrt{4 x^{2} 16}=16 x
2(2 x * 4)=16 x
16 x=16 x
En efecto, es un trinomio cuadrado perfecto, donde a=2 x \text{ y } b=4 . Con signo negativo porque el término del medio es negativo.
(2 x-4)^{2}=4 x^{2}-16 x+16
Entonces: D2.
Concluimos por último: 1C, 2D, 3A, 4B. La opción correcta es la d).
Reactivo 33
Una función _____________ de una variable es aquella que se expresa por medio de un _________ de primer grado.
- Lineal-termino
- Lineal-polinomio
- Cuadrática-monomio
- Cuadrática-exponente
Solución:
La respuesta de este primer problema radica en examinar la definición de una función lineal. Antes habíamos comentado que:
Una función/ecuación es lineal si la o las variables en ella tienen como máximo exponente la unidad, no están multiplicadas entre ellas y tampoco poseen exponente negativo.
De esto podemos extraer que una función o ecuación lineal no es más que un polinomio de grado 1. Por lo tanto, las palabras que completan correctamente a la frase son lineal-polinomio. Concluimos entonces que la respuesta es la b).
Una función lineal de una variable es aquella que se expresa por medio de un polinomio de primer grado.
Reactivo 34
Identificar las raíces de f(x)=x^{3}+2 x^{2}-11 x-12
- \{-1,3,-4\}
- \{-1,2,-4\}
- \{1,-2,-4\}
- \{1,3,-4\}
Solución:
Primero, comprobamos la naturaleza de las raíces de la función cúbica antes de pasar a aplicar Ruffini. De esta forma, evitamos trabajar innecesariamente en el cálculo.
\Delta=18 a b c d-4 b^{3} d+b^{2} c^{2}-4 c^{3} a-27 a^{2} d^{2}
\Delta=18(1)(2)(-11)(-12)-4(2)^{3}(-12)+(2)^{2}(-11)^{2}-4(-11)^{3}(1)-27(1)^{2}(-12)^{2}
Resolviendo productos y sumas obtenemos como resultado:
\Delta=7056
Tiene tres raíces reales.
Procedemos ahora a factorizar con ayuda de Ruffini:
Se escoge al -1 como primer intento:
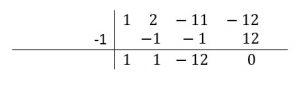
Ya que hemos logrado llevar a cero al término independiente, significa que -1 es una de las raíces del polinomio cúbico. Escribimos ahora a la ecuación de tercer grado en su primera forma factorizada:
x^{3}+2 x^{2}-11 x-12=(x+1)\left(-x^{2}-x+12\right)
Al polinomio de segundo grado se le aplica ahora la ecuación resolvente:
-x^{2}-x+12
x_{2}=\frac{-(-1)+\sqrt{(-1)^{2}-4(-1)(12)}}{2(-1)}=-4
x_{3}=\frac{-(-1)-\sqrt{(-1)^{2}-4(-1)(12)}}{2(-1)}=3
Concluimos entonces que las raíces de la función cúbica son \{-1,3,-4\} . Comparando con las opciones ofrecidas por el problema, la respuesta correcta sería la a).
Reactivo 35
Encontrar el valor de la función f(t)=\frac{2}{9} t^{4}+\frac{1}{3} t^{3}+2 t^{2}-10 \text { en } t=3
- 20
- 35
- 30
- 25
Solución:
En este caso, se nos pide evaluar a la función f(t) cuando t=3 . Se sustituye a t por el valor dado 3, se resuelven las potencias, productos y sumas hasta llegar al valor final.
f(3)=\frac{2}{9}(3)^{4}+\frac{1}{3}(3)^{3}+2(3)^{2}-10
Resolvemos las potencias correspondientes
f(3)=\frac{2}{9}(81)+\frac{1}{3}(27)+2(9)-10
Ahora, los productos
f(3)=18+9+18-10
Por último, las sumas y restas para obtener el valor de f(t) cuando t=3
f(3)=35
La respuesta correcta seria la b).
Reactivo 36
Elegir el término A_{n} en el desarrollo del producto de n factores lineales de la siguiente expresión: \left(x-a_{1}\right)\left(x-a_{2}\right) \ldots\left(x-a_{n}\right)=x^{n}+A_{1} x^{n-1}+A_{2} x^{n-2}+\cdots+A_{n} . Considerando que a_{1}, a_{2}, \ldots, a_{n} son números reales.
- (-1)^{n+1} a_{1} a_{2} \ldots a_{n}
- (-1)^{n} a_{1} a_{2} \ldots a_{n}
- -a_{1} a_{2} \ldots a_{n}
- a_{1} a_{2} \ldots a_{n}
Solución:
Para encontrar respuesta a este problema, debemos desarrollar el producto de los n factores que componen al polinomio de enésimo grado.
Analizando un poco antes de continuar, nos damos cuenta que el término A_{n} de dicha expansión es el independiente, es decir, solo está compuesto por el producto de los a_{1}, a_{2}, \ldots, a_{n} . Procedemos entonces a escribir la siguiente igualdad:
A_{n}=\left(-a_{1}\right)\left(-a_{2}\right)\left(-a_{3}\right) \ldots\left(-a_{n}\right)
De ella, comprobamos que: si n es par el resultado será un número positivo, de lo contrario será negativo, por lo que podemos extraer el menos factor común y expresarlo como:
A_{n}=(-1)^{n} a_{1} a_{2} \ldots a_{n}
De tal forma que:
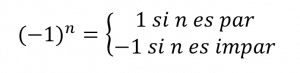
Conclusión, la respuesta correcta es la b). Como dato extra, el término puede escribirse como:
A_{n}=(-1)^{n} \prod_{j=1}^{n} a_{j}
Reactivo 37
Determinar el valor para x que satisface la igualdad: \frac{5}{x-3}=\frac{33-x}{x^{2}-6 x+9}
- -12
- -8
- 8
- 12
Paso 1: simplificar las fracciones en ambos lados de la ecuación. Para eso, procedemos a multiplicar ambos miembros por los polinomios de los denominadores de cada fracción.
¡Recuerda! Para mantener la igualdad, se debe realizar la operación en ambos miembros.
\frac{5}{x-3}=\frac{33-x}{x^{2}-6 x+9}
Multiplicamos ambos lados por x^{2}-6 x+9.
\frac{5}{x-3}\left(x^{2}-6 x+9\right)=\frac{33-x}{x^{2}-6 x+9}\left(x^{2}-6 x+9\right)
\frac{5\left(x^{2}-6 x+9\right)}{x-3}=\frac{\left(x^{2}-6 x+9\right)(33-x)}{x^{2}-6 x+9}
Simplificamos a x^{2}-6 x+9 en el numerador y denominador del segundo miembro.
\frac{5\left(x^{2}-6 x+9\right)}{x-3}=(33-x) \frac{x^{2}-6 x+9}{x^{2}-6 x+9}
\frac{5\left(x^{2}-6 x+9\right)}{x-3}=(1)(33-x) \rightarrow \frac{5\left(x^{2}-6 x+9\right)}{x-3}=33-x
Hacemos lo mismo con x-3.
\frac{5\left(x^{2}-6 x+9\right)}{x-3}(x-3)=(33-x)(x-3)
Simplificamos a x-3 en el numerador y denominador del primer miembro.
5\left(x^{2}-6 x+9\right) \frac{x-3}{x-3}=(33-x)(x-3)
5\left(x^{2}-6 x+9\right)(1)=(33-x)(x-3) \rightarrow 5\left(x^{2}-6 x+9\right)=(33-x)(x-3)
Paso 2: resolvemos los productos entre polinomios a ambos lados de la ecuación, aplicando el método en la multiplicación de polinomios.
5\left(x^{2}-6 x+9\right)=(33-x)(x-3)
5 * x^{2}-5 * 6 x+5 * 9=33(x-3)-x(x-3)
5 x^{2}-30 x+45=33 x-99-x^{2}+3 x
Paso 3: agrupamos los términos de la ecuación en un mismo miembro. Por convención, cuando se despeja una variable se agrupan los términos en el primer miembro.
¡Recuerda! Si un término está sumando, se resta a ambos lados de la ecuación por el término para llevarlo al otro miembro.
De la explicación anterior, se deduce la regla nemotécnica que dice: si un término está restando pasa al otro lado sumando y viceversa. Aplica el mismo principio para la multiplicación y división.
Teniendo esto claro, procedemos a agrupar los términos al primer miembro.
5 x^{2}-30 x+45-33 x+99+x^{2}-3 x=0
5 x^{2}+x^{2}-30 x-33 x-3 x+45+99=0
Resolvemos sumas y restas.
6 x^{2}-66 x+144=0
Para encontrar los valores que satisfacen la igualdad es necesario resolver la ecuación de segundo grado.
Paso 4: aplicamos la fórmula cuadrática para hallar las raíces de la ecuación.
x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \rightarrow a x^{2}+b x+c
En nuestro caso, estos serían los valores de a, b y c.
a=6 \quad b=-66 \quad c=144
Sustituimos los valores en la formula cuadrática.
x=\frac{-(-66) \pm \sqrt{(-66)^{2}-4(6)(144)}}{2(6)}=\frac{66 \pm \sqrt{4356-3456}}{12}
Hallamos finalmente x_{1} y x_{2}:
x_{1}=\frac{66+\sqrt{4356-3456}}{12}=8
x_{2}=\frac{66-\sqrt{4356-3456}}{12}=3
La respuesta correcta al ejercicio es la opción c).
Reactivo 38
Determinar el valor de la literal “a” que satisfaga la siguiente igualdad, tomando en cuenta que x \neq 0 :
\frac{\sqrt[3]{x^{2}} \sqrt[4]{x^{a}}}{\sqrt{x^{5}}}=1
- -\frac{22}{3}
- -\frac{28}{15}
- \frac{28}{15}
- \frac{22}{3}
Solución:
A primera vista, parece que la ecuación no es lineal, pero trabajemos un poco al primer miembro de la igualdad aplicando leyes de exponentes:
\frac{\sqrt[3]{x^{2}} \sqrt[4]{x^{a}}}{\sqrt{x^{5}}}=\frac{x^{\frac{2}{3}} x^{\frac{a}{4}}}{x^{\frac{5}{2}}}=x^{\frac{2}{3}+\frac{a}{4}-\frac{5}{2}}
x^{\frac{2}{3}+\frac{a}{4}-\frac{5}{2}}=1
Para que esta igualdad sea cierta siempre que x \neq 0 , el exponente de dicha variable debe ser cero, tal como dice la propiedad de los exponentes:
a^{0}=1
Por lo tanto:
\frac{2}{3}+\frac{a}{4}-\frac{5}{2}=0
Luego del análisis, la solución al problema radica en resolver una ecuación lineal.
\frac{a}{4}=\frac{5}{2}-\frac{2}{3} \rightarrow a=\frac{22}{3}
Concluimos entonces que la respuesta correcta es la d).
Reactivo 39
Resolver la siguiente ecuación: 2(5 x+1)-4=3(x-7)-16
- -7
- -5
- 5
- 7
Solución:
En este caso, solo debemos resolver a la ecuación para encontrar el valor de x . Primero, deshacemos las distributivas, luego agrupamos términos literales a la izquierda y numéricos a la derecha:
10 x+2-4=3 x-21-16
10 x-3 x=2-21-16
Resolvemos sumas y despejamos finalmente a x :
7 x=-35 \rightarrow x=-5
Concluimos entonces que la respuesta correcta es la b).
Reactivo 40
¿Cuál opción representa la solución de la ecuación -\frac{1}{a}+3=\frac{2}{a}-9 ?
- a=-\frac{1}{4}
- a=-4
- a=\frac{1}{4}
- a=4
Solución:
Antes de realizar cualquier operación, la ecuación parece ser no lineal, ya que la variable a se encuentra elevada a -1. Si multiplicamos ambos lados de la ecuación por a lograremos transformarla a una ecuación lineal:
-\frac{1}{a}+3=\frac{2}{a}-9 \rightarrow-1+3 a=2-9 a
-1+3 a=2-9 a
Esta ecuación, equivalente a la anterior, es lineal. Procedemos a resolverla:
3 a+9 a=2+1
12 a=3 \rightarrow a=\frac{1}{4}
Concluimos entonces que la opción correcta es la c).


