Examen Simulador IPN de Álgebra: Reactivos del 11 al 20

Vamos a resolver los siguientes 10 ejercicios del simulador de álgebra para el examen de admisión al IPN. Para la segunda parte vamos a resolver los ejercicios del 11 al 20.

Intenta resolverlos por tu cuenta antes de consultar la explicación paso a paso del reactivo.

Reactivo 11

Si una viga de madera de 2 m de largo se divide en dos partes que se encuentran en la proporción de 5:7, y la parte de menor longitud se corta a su vez en dos segmentos con razón de 2:3 ¿Cuánto mide la longitud de la parte más pequeña en que se cortó la viga?

1. 2/3m
2. 1/3m
3. 1/5m
4. 1/7m

Solución

Análisis: para visualizar de una forma más clara, hagamos un bosquejo de cómo quedaría dividida la viga.

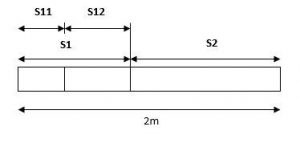
En el diagrama:

• S1 y S2 mitad pequeña y mitad larga de la viga
• S11 y S12 primer y segunda de la mitad más pequeña de la viga (S1)

Teniendo en cuenta que S1 y S2 son las mitades que juntas suman los 2m de la viga, es posible escribir:

s_{1}+s_{2}=2

Si la proporción entre las mitades es 5:7, obtenemos la relación:

\frac{s_{1}}{s_{2}}=\frac{5}{7}

Hay que aclarar que S1 debe ir en el numerador y S2 en el denominador porque el cociente 5:7 es menor a uno, lo que quiere decir que el dividendo es menor que el divisor. Ya que desde el inicio se asumió que S1 sería la mitad menor y S2 la mitad mayor, para que el resultado tenga concordancia hay que ordenarlos de esta manera.

Dicho lo anterior, nos queda un pequeño sistema de 2 ecuaciones con dos incógnitas. Para resolverlo se empleará el método por sustitución.

Despejamos S2:

\frac{s_{1}}{s_{2}}=\frac{5}{7} \rightarrow s_{2}=\frac{7}{5}s_{1}

Para luego sustituirlo en la primera ecuación:

\frac{7}{5}s_{1}+s_{1}=2\rightarrow \frac{12}{5}s_{1}=2\\\Rightarrow s_{1}=\frac{5}{6}

Podríamos calcular a S2, pero no es relevante para el ejercicio, ya que lo solicitado se encuentra en la mitad menor, es decir S1.

Ahora, toca hacer el mismo análisis para determinar el segmento más pequeño en la menor mitad. En la ilustración, se hace notar que S11 es el segmento menor de S1. Con el análisis hecho, queda calcular a S11.

s_{11}+s_{21}=\frac{5}{6} \text{ y }\frac{s_{11}}{s_{21}}=\frac{2}{3}

Despejamos a S21 y se sustituye en la ecuación s_{11}+s_{21}=\frac{5}{6}:

\frac{s_{11}}{s_{21}}=\frac{2}{3}\rightarrow s_{21}=\frac{3}{2}s_{11}\\ \text{sustituyendo: }s_{11}+\frac{3}{2}s_{11}=\frac{5}{6}\rightarrow \frac{5}{2}s_{11}=\frac{5}{6}\\ \therefore s_{11}=\frac{1}{3}

Conclusión: el valor de la longitud más pequeña en la viga es s_{11}=\frac{1}{3}m. La opción a seleccionar es la b).

Reactivo 12

Relacionar cada enunciado con la proporción que le corresponde:

 

1. 1. 1A, 2D, 3C, 4B
   2. 1A, 2D, 3B, 4C
   3. 1C, 2A, 3D, 4B
   4. 1C, 2A, 3B, 4D

Solución:

Para resolver este problema, es necesario inspeccionar cada una de las fracciones en la columna derecha.

• La fracción \frac{4}{64} puede también expresarse como 4: 64 en notación de razón. Si la comparamos con las opciones en la columna derecha, queda claro que corresponde a la opción 2. Si 4 es a 64. Por lo tanto, 2A.
• La igualdad \frac{3}{4}=\frac{7}{6} es falsa, ya que no hay manera de que dichas fracciones sean equivalentes entre sí ¿razón? El número 3 y el numero 7 son primos, esto descarta por completo la posibilidad de equivalencia.

Además, tampoco hay un entero que multiplicado por el 4 de como resultado al número 6. Conclusión: la fracción B va emparejada con la opción 4. Proposición falsa 4B.

• La igualdad de fracciones \frac{2}{9}=\frac{4}{18} es cierta, ya que si multiplicamos y dividimos a la fracción \frac{2}{9} por 2

\frac{2 * 2}{2 * 9}=\frac{4}{18}

Se demuestra que ambas fracciones son equivalentes. Según las opciones en la columna izquierda, la correcta sería la 1. Proporción directa, de esta forma 1C.

• Por simple reducción, es lógico que la proporción D. \frac{180}{120}=\frac{50}{75} corresponda con el enunciado 3. Proporción inversa. Para evitar dejar deducciones sueltas, vamos a demostrarlo.

Como se vio en el apartado teórico, una fracción es inversa a otra si los numeradores y denominadores están intercambiados de lugar. Hay que simplificar ambas fracciones, dividiendo arriba y abajo por un mismo número hasta obtener numeradores y denominadores intercambiados.

\frac{180}{120}=\frac{50}{75}

Probamos con el 5, ya que todos los números son divisibles entre el 5.

\frac{\frac{180}{5}}{\frac{120}{5}}=\frac{\frac{50}{5}}{\frac{75}{5}}

\frac{36}{24}=\frac{10}{15}

En la primera fracción podemos dividir por 6 y en la segunda por 5 nuevamente.

\frac{\frac{36}{6}}{\frac{24}{6}}=\frac{\frac{10}{5}}{\frac{15}{5}}

\frac{6}{4}=\frac{2}{3}

Por último, se divide la primera fracción por 2. La segunda es irreducible, porque está siendo representada por números primos.

\frac{\frac{6}{2}}{\frac{4}{2}}=\frac{2}{3}

\frac{3}{2}=\frac{2}{3}

De esta manera queda evidenciado que ambas son fracciones inversas. Concluimos la respuesta al problema: 1C, 2A, 3D, 4B. Que según las opciones que ofrece el enunciado, la correcta es la c).

Reactivo 13

Transformar a lenguaje algebraico:

\text { La división de un número entero entre su sucesor. }

1. \frac{x}{x}
2. \frac{x}{1-x}
3. \frac{x-1}{x}
4. \frac{x}{x+1}

Solución:

En este caso, la relación en forma de enunciado o lenguaje común es como la de los ejemplos vistos antes. Analizamos la frase por partes:

La división indica que las cantidades mencionadas a continuación se dividen. La primera mencionada va como numerador y la siguiente como denominador.

… Un número entero hace alusión a una variable x que pertenece a los enteros.

… Su sucesor, como se indicó en los casos particulares para la suma, el sucesor de un número es el sumado uno x+1 .

Concluimos entonces que, la traducción a lenguaje algebraico es:

\frac{x}{x+1}

En conclusión, la respuesta correcta es la d).

Reactivo 14

Encontrar dos números tales que el doble de su suma sea igual al triple de su diferencia más 8; además, su semisuma debe ser igual a su diferencia más 1.

1. -7, 3
2. -7, -3
3. 7, 3
4. 7, -3

Solución:

El problema enuncia de manera general que hay dos números, a los que podremos considerar como las variables del enunciado. Junto a ellas, se indican como están relacionadas entre sí con las frases:

\text { ...el doble de su suma sea igual al triple de su diferencia más } 8…

\text { ...su semisuma debe ser igual a su diferencia más } 1…

Aplicando los mismos principios que en problemas anteriores, se deducen las expresiones algebraicas partiendo de las frases en lenguaje natural:

\text { variables: } x, y

2(x+y)=3(x-y)+8

\frac{x+y}{2}=x-y+1

Para encontrar el valor de las variables, solo hay que resolver el sistema de ecuaciones. Ahora, ordenamos antes las ecuaciones y luego aplicamos el método por reducción.

Ecuación 1:

2(x+y)=3(x-y)+8

2 x+2 y=3 x-3 y+8

2 x-3 x+2 y+3 y=8

-x+5 y=8

Ecuación 2:

\frac{x+y}{2}=x-y+1

x+y=2 x-2 y+2

x-2 x+y+2 y=2

-x+3 y=2

Ahora, el sistema de ecuaciones queda entonces:

I:-x+5 y=8

I I:-x+3 y=2

Hacemos -I+I I :

x-5 y=-8

-x+3 y=2

\therefore-2 y=-6 \rightarrow y=3

Sustituimos en la Ecuación 1 para encontrar el valor de x :

x-5(3)=-8

x-15=-8

x=15-8 \rightarrow x=7

Concluimos entonces que, la respuesta correcta es la c). x=7 \text { y } y=3

Reactivo 15

¿Qué expresión representa al enunciado “La raíz cuadrada del cociente de la suma de dos números entre su diferencia”?

1. \frac{\sqrt{a+b}}{a-b}
2. \sqrt{\frac{a+b}{a-b}}
3. \frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}
4. (\sqrt{a+b})(a-b)

Solución:

Para este problema, se ha presentado otra operación: la raíz cuadrada… Que indica de manera explícita que el resto del enunciado está encerrado dentro de una raíz cuadrada. Aclarado este punto, analizamos la frase:

La raíz cuadrada hace alusión a la raíz cuadrada de lo siguiente.

… Cociente de la, indica que se hará el cociente entre las siguientes cantidades.

… La suma de dos números, dos variables x y y  serán sumadas.

… Su diferencia, de las dos variables anteriores su resta.

Concluimos entonces que, la traducción a lenguaje algebraico es:

\sqrt{\frac{a+b}{a-b}}

En conclusión, la respuesta correcta es la b).

Reactivo 16

En un gallinero hay p pollos. Se enfermó la mitad y luego la mitad del resto. Los pollos sanos son:

1. 0
2. \frac{p}{4}
3. \frac{p}{3}
4. \frac{p}{2}

Solución:

En este caso la dificultad ha incrementado un poco, además de un enunciado en lenguaje común es necesario analizar matemáticamente el problema.

Antes de que se enfermaran los pollos, las cantidades en inicio son:

\text { Enfermos }=0 \text { y Sanos }=p

Cuando se enferma la mitad, es claro que la cantidad de pollos sanos disminuye también a la mitad:

\text { Enfermos }=\frac{p}{2} y \text { Sanos }=\frac{p}{2}

La mitad del resto, es decir la mitad de los pollos que ahora están sanos se enferma.

\text { Enfermos }=\frac{p}{2}+\frac{p}{2} * \frac{1}{2} y \text { Sanos }=\frac{p}{2} * \frac{1}{2}

\text { Enfermos }=\frac{p}{2}+\frac{p}{4} y \text { Sanos }=\frac{p}{4}

\text { Enfermos }=\frac{3 p}{4} y \text { Sanos }=\frac{p}{4}

Es posible corroborar el resultado sumando ambas cantidades, la cual debe arrojar  porque es la cantidad total de pollos:

\text { Total }=\text { Enfermos }+\text { Sanos }=\frac{3 p}{4}+\frac{p}{4}=\frac{3 p+p}{4}=\frac{4 p}{4}=p

Concluimos entonces que, la respuesta correcta es la b). Quedan \frac{p}{4} pollos sanos.

Reactivo 17

Identifica la forma simplificada de la fracción siguiente: \frac{4\left[1+\left(\frac{z}{R}\right)^{2}\right]}{\left[4 R^{2}+(2 z)^{2}\right]^{\frac{3}{2}}}

1. \frac{\left[1+\left(\frac{z}{R}\right)^{2}\right]^{2}}{\left[R^{2}+(z)^{2}\right]^{\frac{1}{2}}}
2. \frac{1}{\sqrt{1+\left(\frac{z}{R}\right)^{2}}}
3. \frac{1}{2 R^{3}} \frac{1}{\sqrt{1+\left(\frac{z}{R}\right)^{2}}}
4. \frac{\left[1+\left(\frac{z}{R}\right)^{2}\right]}{\left[R^{2}+z^{2}\right]^{\frac{1}{2}}}

Solución:

Para resolver este primer problema, es necesario alterar alguna de las partes de la fracción para que se parezcan y luego poder realizar una simplificación de exponentes con la misma base. En este caso, resulta más sencillo trabajar la expresión del denominador.

Para evitar escribir demasiado, vamos a trabajar la expresión extrayéndola de momento, de la fracción.

\left[4 R^{2}+(2 z)^{2}\right]^{\frac{3}{2}}

Resolvemos la potencia de (2 z)^{2} y sacamos factor común el 4:

\left[4 R^{2}+(2 z)^{2}\right]^{\frac{3}{2}}=\left[4 R^{2}+4 z^{2}\right]^{\frac{3}{2}}=\left[4\left(R^{2}+z^{2}\right)\right]^{\frac{3}{2}}

Para asemejar la expresión a la del numerador, es necesario extraer también como factor común a R^{2} :

\left[4\left(R^{2}+z^{2}\right)\right]^{\frac{3}{2}}=\left[4 R^{2}\left(1+\frac{z^{2}}{R^{2}}\right)\right]^{\frac{3}{2}}=\left[4 R^{2}\left(1+\left(\frac{z}{R}\right)^{2}\right)\right]^{\frac{3}{2}}

Por último, se saca al factor 4 R^{2} del exponente \frac{3}{2} :

\left(4 R^{2}\right)^{\frac{3}{2}}\left[1+\left(\frac{Z}{R}\right)^{2}\right]^{\frac{3}{2}}=4^{\frac{3}{2}}\left(R^{2}\right)^{\frac{3}{2}}\left[1+\left(\frac{Z}{R}\right)^{2}\right]^{\frac{3}{2}}

4^{\frac{3}{2}}\left(R^{2}\right)^{\frac{3}{2}}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{3}{2}}=8 R^{3}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{3}{2}}

La expresión que hemos conseguido, gracias a manipulaciones sustentadas en las propiedades de la potenciación, el producto y la suma es idéntica a la que se encuentra en el numerador. Pasamos ahora a sustituir y simplificar.

\frac{4\left[1+\left(\frac{z}{R}\right)^{2}\right]}{8 R^{3}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{3}{2}}}=\frac{4}{8 R^{3}} \frac{\left[1+\left(\frac{z}{R}\right)^{2}\right]}{\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{3}{2}}}=\frac{1}{2 R^{3}} \frac{\left[1+\left(\frac{z}{R}\right)^{2}\right]}{\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{3}{2}}}

Ahora, se puede aplicar la propiedad de división de potencias de igual base:

\frac{1}{2 R^{3}} \frac{\left[1+\left(\frac{Z}{R}\right)^{2}\right]}{\left[1+\left(\frac{Z}{R}\right)^{2}\right]^{\frac{3}{2}}}=\frac{1}{2 R^{3}}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{1-\frac{3}{2}}=\frac{1}{2 R^{3}}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{-\frac{1}{2}}

Por último, acomodamos la expresión resultante con la propiedad de exponente inverso y con la propiedad del exponente fraccionario.

\frac{1}{2 R^{3}}\left[1+\left(\frac{z}{R}\right)^{2}\right]^{-\frac{1}{2}}=\frac{1}{2 R^{3}} \frac{1}{\left[1+\left(\frac{z}{R}\right)^{2}\right]^{\frac{1}{2}}}=\frac{1}{2 R^{3}} \frac{1}{\sqrt{1+\left(\frac{z}{R}\right)^{2}}}

Concluimos entonces que: la respuesta correcta es la c).

Reactivo 18

Simplificar la siguiente expresión con fracciones: \frac{1}{a+b}-\frac{a}{(a+b)^{2}}-\frac{b^{2}}{(a+b)^{3}}

1. -\frac{a b}{(a+b)^{3}}
2. \frac{a b}{(a+b)^{2}}
3. \frac{a b}{(a+b)^{3}}
4. -\frac{a b}{(a+b)^{2}}

Solución:

Para dar solución a este problema, aplicaremos el método de mínimo común múltiplo con la justificación de que:

• Supone reducir la cantidad de operaciones a realizar
• La cantidad de fracciones involucradas es mayor a 2

Paso 1: calculamos el mínimo común múltiplo de los denominadores de las tres fracciones.

\operatorname{mcm}\left(a+b,(a+b)^{2},(a+b)^{3}\right)

Si tratamos a los binomios como un solo objeto algebraico, el mínimo común múltiplo de los tres elementos es el de mayor grado, por lo tanto:

\operatorname{mcm}\left(a+b,(a+b)^{2},(a+b)^{3}\right)=(a+b)^{3}

Paso 2: se divide el mcm entre los denominadores de cada fracción.

F_{1}=\frac{(a+b)^{3}}{a+b}=(a+b)^{2}

F_{2}=\frac{(a+b)^{3}}{(a+b)^{2}}=a+b

F_{3}=\frac{(a+b)^{3}}{(a+b)^{3}}=1

Paso 3: se multiplican y dividen las fracciones, para luego hacer la suma directa.

\frac{(a+b)^{2}}{(a+b)^{3}}-\frac{a(a+b)}{(a+b)^{3}}-\frac{b^{2}}{(a+b)^{3}}

\frac{(a+b)^{2}-a(a+b)-b^{2}}{(a+b)^{3}}

Se desarrolla el producto notable (a+b)^{2} , la distributiva a(a+b) y las sumas y restas pertinentes.

\frac{a^{2}+2 a b+b^{2}-a^{2}-a b-b^{2}}{(a+b)^{3}}

\frac{a b}{(a+b)^{3}}

Comparando con las opciones del problema, la respuesta correcta es c).

Reactivo 19

Resolver la suma de fracciones algebraicas: \frac{x+4}{2}+\frac{x+1}{3}

1. \frac{5 x+14}{6}
2. \frac{2 x+14}{5}
3. \frac{5 x+5}{6}
4. \frac{2 x+5}{5}

Solución:

Este problema es similar al anterior y su solución pasa por resolver la suma de fracciones. En este caso no es necesario aplicar la técnica del mcm, ya que no hay más de 2 fracciones y los denominadores son números enteros.

Aplicamos el producto cruzado para la suma de fracciones:

\frac{x+4}{2}+\frac{x+1}{3}=\frac{3(x+4)+2(x+1)}{2 * 3}=\frac{3 x+12+2 x+2}{6}=\frac{5 x+14}{6}

En conclusión, la respuesta correcta es la a).

Reactivo 20

Asociar cada número decimal con la representación en fracciones que le corresponde.

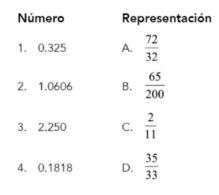
1. 1B, 2D, 3C, 4A
2. 1B, 2D, 3A, 4C
3. 1C, 2A, 3D, 4B
4. 1C, 2A, 3B, 4D

Solución:

Tenemos diferentes caminos para dar solución a este problema. El primero sería convertir los decimales exactos a fracciones y el segundo consta en realizar la división de los números fraccionarios.

En este caso, vamos a escoger el camino de dividir los números indicados en cada fracción. La justificación para esto es que: no sabemos si los decimales en la columna izquierda han sido truncados, lo que nos puede llevar a resultados diferentes a los exhibidos en la columna derecha.

Fracción A. \frac{72}{32} :

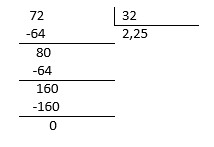
Comparando con las columnas: 3A.

Fracción B. \frac{65}{200} :

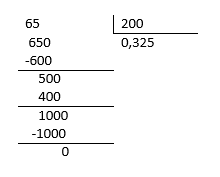
Comparando con las columnas: 1B.

Fracción C. \frac{2}{11} :

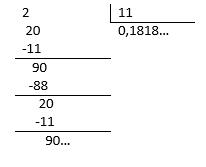
En este caso, el cociente entre los números de la fracción arroja un decimal periódico puro y aunque se le asemeja a la opción 4. de la columna izquierda, en dicha cantidad nunca se indica que sea periódica. De haber escogido el método de componer la fracción, el resultado habría sido incorrecto.

Dejando clara la observación, se puede concluir que: 4C.

Fracción D. \frac{35}{33} . El procedimiento es el mismo para la división. Nuevamente, se presenta un caso periódico 1,0606… y aunque no se indique en los resultados de la tabla, se escoge como correcta la opción 2. Concluimos que: 2D.

Respuesta al problema opción b) 1B, 2D, 3A, 4C.