Resuelve el examen simulacro de matemáticas para el IPN correspondiente a la parte de álgebra. El simulador consta de 50 reactivos que te ayudarán a reforzar tus conocimientos para presentar el examen de ingreso al Instituto Politécnico Nacional.

Los 50 reactivos que vienen en tu examen simulador cubren la mayoría de los temas de la guía más reciente.
Para hacer tu rutina de estudio más eficiente hemos dividido los ejercicios en tres partes, para que puedas tomar los descansos necesarios y consolidad tus conocimientos.
Estructura del Examen IPN
El examen de ingreso al IPN se divide en un módulo de conocimientos generales, en el cual las materias son comunes a todas las carreras ofertadas e incluye:
- Matemáticas
- Competencia escrita
- Competencia lectora
- Reading comprehension (nuevo tema)
- Historia
Y, el módulo de conocimientos experimentales en el que se evalúa biología, química y física. En este último la dificultad varía según la carrera elegida, ya que se agrupan en tres grandes ramas del conocimiento:
- IyCFM: Ingeniería y ciencias físico matemáticas.
- CMD: Ciencias médico biológicas.
- CSyA: Ciencias sociales y administrativas.
Ingresar en el IPN no es tarea fácil, por ello, apóyate en cada una de las herramientas que colocamos a tu disposición y si tienes algunas dudas la siguiente tabla muestra la estructura de reactivos por materia para cada área:
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Temario álgebra
El apartado de matemáticas suele ser un gran reto para muchos aspirantes, por ello, este examen simulador tiene como objetivo afianzar tus conocimientos a través de la práctica continua, para alcanzar los aciertos necesarios.
- Álgebra
- Números reales
- Propiedades
- Operaciones básicas
- Proporciones
- Expresiones algebraicas
- Lenguaje algebraico
- Expresiones fraccionarias
- Leyes de los exponentes y los radicales
- Productos notables
- Métodos de factorización
- Funciones y ecuaciones lineales
- Concepto de función
- Propiedades de las desigualdades
- Ecuaciones lineales
- Sistemas de ecuaciones lineales
- Funciones y ecuaciones cuadráticas
- Concepto de función cuadrática
- Ecuaciones cuadráticas
- Números reales
Reactivo 1
En la siguiente igualdad 3 \sqrt{5}+3\sqrt{7}=3(\sqrt{5}+\sqrt{7}) se ejemplifica la propiedad ___________ de los números reales.
- Asociativa
- Distributiva
- Conmutativa
- Neutro aditiva
Solución:
Si comparas la igualdad con las propiedades vistas en el apartado anterior, queda claro de inmediato que la respuesta correcta es la b) Propiedad Distributiva.
¿Por qué es Distributiva? Si examinas la igualdad con atención y recuerdas la forma de la propiedad distributiva: a*b+c=a*b+a*c te darás cuenta de que el número 3 juega el papel de a, 5 sería b y 7 la letra c.
Reactivo 2
Identificar el conjunto de los primeros 6 números compuestos.
- 1, 3, 5, 7, 9, 11,…
- 2, 4, 6, 8, 10, 12,…
- 3, 5, 7, 9, 11, 13,…
- 4, 6, 8, 9, 10, 12,…
Análisis:
Para resolver el problema, puedes consultar la serie de 100 primeros números primos para identificar cuáles son primos.
- La opción a) no puede ser correcta, ya que el 3, 5, 7 y 11 son primos y el 1 no se considera compuesto ni primo. El único compuesto es el 9
- La opción b) tampoco puede ser la correcta. Aunque el 4, 6, 8, 10 y 12 son compuestos (2*2,2*3,2*4,2*5 \text{ y } 2*6 respectivamente) el 2 es el primer número primo de la lista
- Al igual que la opción a), la c) también tiene números primos: 3, 5, 7, 11 y 13
- Aunque evidentemente debe ser la d), la razón es porque todos son números compuestos:
4=2*2
6=2*3
8=2*2*2
9=3*3
10=2*5
12=2*2*3
Reactivo 3
Representar como el cociente de dos enteros el siguiente número decimal periódico 0, \overline{1234}
- \frac{1234}{1000}
- \frac{1234}{9999}
- \frac{1234}{10000}
- \frac{1234}{99999}
Análisis:
Según los tipos de decimales cíclicos, el número del problema sería: periódico simple. Ahora solo queda encontrar la fracción generatriz con el método correspondiente y seleccionar la opción correcta.
Encontrar el numerador de la fracción:
\text { numerador }=0, \overline{1234} * 10000-0=1234-0
Encontrar al denominador:
denominador=9999
Formar la fracción:
0, \overline{1234}=\frac{1234-0}{9999}=\frac{1234}{9999}
Por lo tanto:
0, \overline{1234}=\frac{1234}{9999}
Seleccionar la respuesta correcta: con base en las opciones propuestas por el problema, la correcta sería la b).
Reactivo 4
Ordenar de forma ascendente (menor a mayor) las siguientes cantidades:
- \sqrt{2}
- 2*\sqrt{2}
- \frac{\sqrt{2}}{2}
- 2
- 3, 4, 2, 1
- 3, 1, 4, 2
- 2, 3, 4, 1
- 2, 4, 1, 3
Solución:
Para resolver el problema, hay que transformar las expresiones radicales para que tengan el mismo exponente aplicando las propiedades antes vistas.
Paso 1: colocamos en orden las expresiones radicales.
\sqrt{2}, 2 \sqrt{2}, \frac{\sqrt{2}}{2}, 2
Paso 2: hay que incluir a los números que están fuera de las raíces dentro de ellas. Para ello, los elevamos al cuadrado y aplicamos raíz cuadrada sobre ellos. Esto mantiene la igualdad y nos permitirá integrarlos a las otras raíces.
Paso 3: aplicamos la propiedad de potencia de un producto y potencia de una fracción pero en reversa:
\sqrt{2}, \sqrt{2^{2}} * \sqrt{2}, \frac{\sqrt{2}}{\sqrt{2^{2}}}, 2
\frac{b^{n}}{a^{n}}=\left(\frac{b}{a}\right)^{n} \text{ y } a^{n} * b^{n}=(a * b)^{n}
Donde n será \frac{1}{2} según la propiedad de exponente racional.
\sqrt{2},(4)^{\frac{1}{2}} * 2^{\frac{1}{2}}, \frac{2^{\frac{1}{2}}}{4^{\frac{1}{2}}}, 2
\sqrt{2},(4 * 2)^{\frac{1}{2}},\left(\frac{2}{4}\right)^{\frac{1}{2}}, 2
\sqrt{2}, \sqrt{8}, \sqrt{\frac{1}{2}}, 2
Paso4: ahora solo queda incluir al 2 en un radical. Para eso, aplicamos el mismo artificio:
\sqrt{2}, \sqrt{8}, \sqrt{\frac{1}{2}}, \sqrt{2^{2}} \rightarrow \underbrace{\sqrt{2}}_{1}, \underbrace{\sqrt{8}}_{2}, \underbrace{\sqrt{\frac{1}{2}}}_{3}, \underbrace{\sqrt{4}}_{4}
¡Listo! Ya es posible ordenar de manera ascendente los números radicales:
\underbrace{\sqrt{\frac{1}{2}}}_{3}, \underbrace{\sqrt{2}}_{1}, \underbrace{\sqrt{4}}_{4}, \underbrace{\sqrt{8}}_{2}
Conclusión: La respuesta correcta es la b) 3, 1, 4, 2.
Reactivo 5
Al desarrollar la siguiente suma se obtiene: \frac{2}{7-3x}+5
- \frac{7}{7-3x}
- \frac{7}{12-3x}
- \frac{37-15x}{7-3x}
- \frac{15x-37}{7-3x}
Solución:
Para encontrar el desarrollo de la suma hay que identificar las expresiones que se están sumando. En este caso, es una fracción polinómica y un número entero por lo tanto, el desarrollo se lleva a cabo igual que una suma de fracciones aplicando suma y producto de polinomios.
Paso 1: es opcional, pero puedes colocar un uno debajo del 5 para darle más claridad a la resolución. Ten en cuenta que: 5=\frac{5}{1}.
\frac{2}{7-3x}+5= \frac{2}{7-3x}+\frac{5}{1}
Paso 2: aplica el procedimiento para sumar fracciones.
El numerador del resultado será: el numerador de la primera fracción por el denominador de la segunda, más el numerador de la segunda fracción multiplicado por el denominador de la primera.
El denominador del resultado será: el producto de ambos denominadores.
A este procedimiento se le conoce como producto cruzado.
\frac{2}{7-3x}+5= \frac{2+5(7-3x)}{7-3x}
Paso 3: desarrolla los productos, ordena y ejecuta las sumas pendientes. Ahora solo queda resolver los productos polinómicos, en este caso el binomio 7-3x multiplicado por 5.
\frac{2+5*7-5*3x}{7-3x}=\frac{37-15x}{7-3x}
Se puede concluir que:
\frac{2}{7-3x}+5=\frac{37-15x}{7-3x}
Según las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 6
Obtenga el resultado de la siguiente división de polinomios: \frac{2x^3+3x^2-5x-6}{x+1}
- -6x^2+x+2
- -2x^2-x+6
- 2x^2+x-6
- 6x^2-x-2
Solución:
Paso1: ordena los polinomios en forma descendente según sus exponentes y reescribe la división.
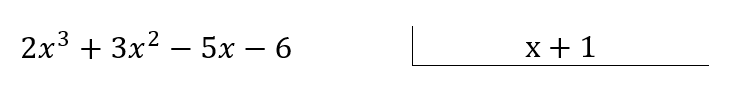
Paso2: encuentra de forma consecutiva los monomios que eliminen al término de mayor grado en el dividendo.
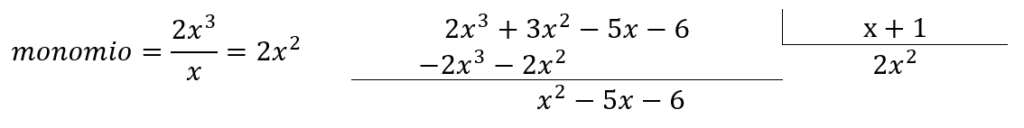
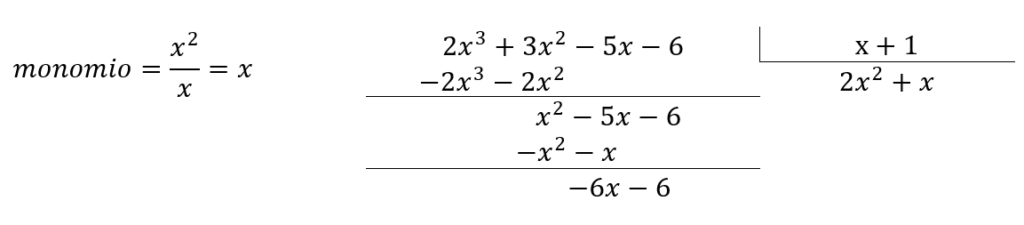
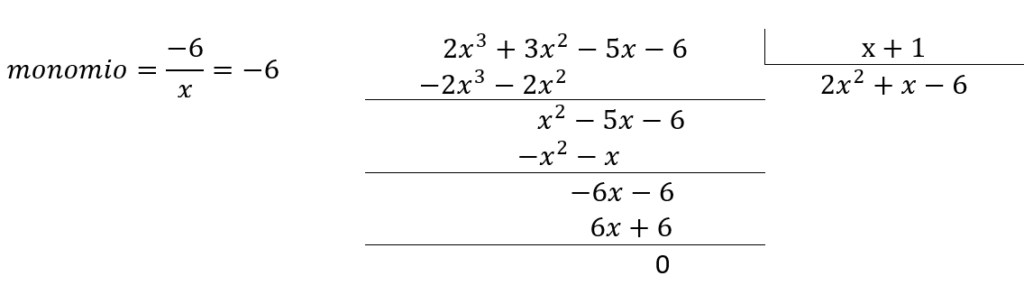
Paso3: culminada la división, obtenemos que el resto es cero. Concluimos que el cociente de ambos polinomios es exacto y se expresa como:
\frac{2x^3+3x^2-5x-6}{x+1}=2x^2+x-6
Según las opciones indicadas en el problema, la correcta sería la c) 2x^2+x-6 .
Continúa practicando y realiza tantos problemas como puedas hasta convertirte en experto. La división de polinomios es un truco que puede sacarte de aprietos al resolver integrales, por lo que vale la pena dedicarle algo de tiempo.
Reactivo 7
María compró por $18 un bolillo, una dona y un pastel. Pedro adquiere por $34 dos bolillos, tres donas y un pastel. Juan paga $54 pesos por cinco bolillos, tres donas y dos pasteles ¿Cuánto cuesta cada alimento?
- Bolillo 4, dona 6 y pastel 8
- Bolillo 3, dona 7 y pastel 8
- Bolillo 2, dona 6 y pastel 10
- Bolillo 2, dona 7 y pastel 9
Solución
Análisis: antes de pensar en escribir ecuaciones, es necesario entender lo que solicita el problema.
Hay que encontrar el precio individual de tres alimentos, específicamente: bolillo, dona y pastel. Esto da una idea que en el problema existen 3 variables cuyo valor, es desconocido.
Además, se especifica que tres niños adquirieron los alimentos en determinadas cantidades y han pagado ciertos montos por ellos. A partir de la compra de cada uno, podemos establecer las primeras relaciones entre las incógnitas del problema:
María
Bolillo + Dona + Pastel ha pagado $18
Pedro
2*Bolillo + 3*Dona + Pastel ha pagado $34
Juan
5*Bolillo + 3*Dona + 2*Pastel ha pagado $54
Cada una de las relaciones se asemeja a una ecuación con 3 incógnitas igualadas a un valor. Para simplificar la escritura, nos referiremos a cada variable como:
Bolillo = x, Dona = y, Pastel = z
Reescribiendo las ecuaciones:
María
x + y +z = 18
Pedro
2x + 3y + z = 34
Juan
5x + 3y + 2z = 54
Forman un sistema de 3 ecuaciones lineales con 3 incógnitas. Una vez resuelto el sistema se conocerá el valor de cada incógnita.
Existen diferentes métodos para resolver sistemas de ecuaciones lineales: igualación, sustitución, reducción o Gauss-Jordan. Puedes emplear cualquiera estudiado con anterioridad.
Esta vez, se resolverá el sistema mediante el método de reducción.
Modelo matemático del problema: sistema de 3 ecuaciones lineales con 3 incógnitas.
\begin{cases}M: x + y +z = 18\\P: 2x + 3y + z = 34\\J: 5x + 3y + 2z = 54\end{cases}
Aplicando el método de reducción:
Paso1: hacemos -2M + P.
-2M:-2x-2y-2z=-36
P:2x+3y+z=34
I: y-z=-2
Paso2: hacemos -5M + J.
-5M:-5x-5y-5z=-90
P:5x+3y+2z=54
II: y-z=-2
Paso3: hacemos -2I + II.
-2I:-2y-2z=4
II:2y+3z=36
\therefore5z=40\rightarrow z=8
Paso4: encontramos el valor de x y y .
Sustituimos z=8 en I para calcular a y:
y-(8)=-2\rightarrow y=8-2\\\therefore y=6
Sustituimos z=8 y y=6 en M para calcular a x:
x+(6)+(8)=18\rightarrow x=18-8-6\\\therefore x=4
De esta manera concluimos que:
x = Bolillo=\$4
y = Dona=\$6
z = Pastel=\$8
La respuesta correcta es la a).
Reactivo 8
Un vecino vende un terreno rectangular en Acapulco y menciona que el área total es 480m^{2}, pero no recuerda las dimensiones de dicho terreno. Si el único dato que tiene es que el largo del terreno es tres veces el frente, menos cuatro metros ¿Cuáles serán las dimensiones del terreno?
- Ancho 10, largo 48
- Ancho 15, largo 32
- Ancho 16/3, largo 90
- Ancho 40/3, largo 36
Solución
Análisis: para resolver este problema, solo hay que recordar la fórmula: A=frente*largo=f*l que sirve para calcular el área de un rectángulo.
Por otro lado, el frente f y el largo l del terreno son las variables del problema.
Lo único que conocemos de ellas es como se relacionan entre sí. De la frase: … el largo del terreno es tres veces el frente menos cuatro metros… se extrae la expresión:
l=3f-4
Que junto a la fórmula del área del rectángulo, se obtiene un sistema de 2 ecuaciones con 2 incógnitas:
\begin{cases}l=3f-4\\fl=480\end{cases}
El método para resolverlo será el de sustitución. Sustituimos la relación dada por el problema en la fórmula del área y luego se despeja el valor de f.
f(3f-4)=480\rightarrow3f^{2}-4f=480\\3f^{2}-4f-480=0
Se aplica la fórmula cuadrática para calcular a f:
\frac{-b\pm\sqrt{b^2-4ac}}{2a}
Para el caso de 3f^{2}-4f-480=0, el valor de los coeficientes es:
a=3;b=-4;c=-480
Sustituyendo y evaluando en la fórmula cuadrática se obtiene:
f=\frac{40}{3}\text{ y }f=-12
Por lógica, el único valor posible para el frente es f=\frac{40}{3}, debido a que no existen longitudes físicas negativas. Para calcular el valor del largo l, se sustituye el resultado obtenido para el frente en la relación dada:
l=3\left(\frac{40}{3}\right)-4=40-4=36
Conclusión: el frente del terreno mide f=\frac{40}{3} \text{m} y el largo 36 \text{m} . La respuesta correcta según el problema es la opción d).
Reactivo 9
¿Cuáles de las siguientes expresiones son polinomios?
- \frac{1}{x}+x
- 3x^2-4x+6
- 2\sqrt{x}-2x+2
- 4x^3-2x-4
- 1, 3
- 1, 4
- 2, 3
- 2, 4
Solución:
La respuesta a este problema es teórica. Radica en recordar los conceptos ya estudiados sobre polinomios y analizar cada uno de los casos.
¡Recuerda! Un polinomio es una suma de términos, cada uno compuesto por: un coeficiente en los reales, una letra que representa a la variable y un exponente en los naturales, es decir, entero positivo.
Con lo anterior en mente, analicemos cada una de las opciones:
- La expresión No cumple con la definición de polinomio. Si aplicamos la propiedad del exponente negativo al primer término se tiene que:
\frac{1}{x}+x =x^{-1}+x
Al tener exponente negativo uno de los términos, no califica como polinomio
- La expresión Si cumple con la definición de polinomio, ya que todos los exponentes son enteros positivos
- La expresión No cumple la definición de polinomio. Si aplicamos la propiedad de exponente racional, se obtiene que:
2\sqrt{x}-2x+2 =2x^{\frac{1}{2}}-2x+2
El exponente es positivo, pero no entero, por lo que no califica como polinomio
- La expresión Si cumple con la definición de polinomio, todos sus términos poseen exponentes en los naturales
Analizada cada expresión, podemos concluir que: 2 y 4 son expresiones polinómicas, por lo tanto, la respuesta correcta es la d).
Reactivo 10
Luis viaja en su auto y recorre el día lunes 100 km en 2 horas. Se ha percatado que el día martes recorre 10 km en 9.6 minutos ¿En qué porcentaje Luis disminuye su tiempo al trasladarse?
- 10
- 15
- 20
- 30
Solución
Análisis: para calcular la diferencia porcentual, primero hay que relacionar los datos que proporciona el problema. Ten en cuenta que no se puede calcular de manera directa lo requerido con los tiempos dados, porque se tomaron con base en distancias distintas. Una para 100 km y otra para 10 km.
Una forma de relacionarlas, es mediante una equivalencia entre las distancias para así obtener un tiempo de referencia y luego compararlo con el que ha proporcionado el problema.
Partiendo del recorrido hecho el lunes tenemos que:
100km\rightarrow2h
Se convierte el tiempo a minutos para mantener unidades homogéneas:
100km\rightarrow120min
¿Cuánto tiempo debió tardar Luis en recorrer 10 km?
100km\rightarrow120min\\ 10km\rightarrow x
x=\frac{10km*120min}{100km}=12min
Esto nos dice que: Luis, en referencia al primer recorrido, debería tardarse 12 minutos en viajar 10 km. Si comparamos este resultado con lo señalado por el problema, vemos que Luis ha tardado menos tiempo: 9.6 minutos.
Con ambos valores, es posible calcular cuál es la disminución porcentual del tiempo que ha tardado Luis (9.6 minutos) respecto al tiempo estimado (12 minutos).
\Delta\%=\frac{\text{tiempo teorico}-\text{tiempo real}}{\text{tiempo teorico}}*100
\Delta\%=\frac{12min-9.6min}{12min}*100=20\%
Conclusión: Luis ha disminuido el tiempo que tarda en trasladarse en un 20%. La opción a seleccionar es la c).

