¡Hola aspirante! Con este examen simulador resuelto de física podrás repasar todos los temas antes del examen de admisión al IPN a las carreras del área de Ingenieria y Ciencias Físico Matemáticas.
En este tutorial vamos a resolver 50 ejercicios de los temas de la guía oficial del IPN (¡la nueva!).

Para hacer efectiva tu ruta de aprendizaje es esencial que conozcas todos los detalles acerca del examen de ingreso. Por ello, hemos realizado una lista resumen con los puntos que no debes pasar por alto de la prueba y a lo largo del post te explicamos los cambios que vendrán este año en el examen del IPN:
- Carreras ofertadas en IPN: 70+
- Porcentaje de aceptación: 20%
- Preguntas en el examen de admisión: 140 preguntas
- Nuevos temas: Historia e Inglés (reading comprehension)
- Tipo: selección múltiple
Estructura Examen IPN
La prueba de ingreso al Politécnico Nacional está dividida en dos bloques: conocimientos generales y conocimientos experimentales. Sin embargo, la cantidad de reactivos va a cambiar segun la rama a la que pertenece tu carrera.
¿Cuáles son las áreas del IPN? Las carreras ofertadas en el Instituto Politécnico Nacional se distribuyen en tres grandes ramas que son:
- IyCFM: Ingeniería y ciencias físico matemáticas
- CMD: Ciencias médico biológicas
- CSyA: Ciencias sociales y administrativas
La siguiente tabla muestra la estructura de reactivos por materia para cada área:
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Los cambios realizados en la prueba del IPN para este año son los siguientes:
- El examen evaluará la materia de inglés, específicamente en el tema de Reading comprehension.
- Las materias de competencia escrita y competencia lectora, sustituyeron a producción escrita y comprensión de textos.
- Cada área asigna la cantidad de reactivos por materia.
- Se agregó la materia de historia de México a las tres áreas de estudio.
- El examen para todas las carreras tendrá 140 reactivos (anteriormente eran 130).
Temario de Física
Esta lista contiene los temas de física que debes dominar antes de presentar:
- Física para IyCFM
- Sistemas de unidades y mediciones
- Álgebra vectorial
- Estática
- Cinemática
- Leyes de Newton
- Propiedades de la materia
- Termodinámica
- Electrostática
- Electrodinámica
- Celdas electroquímicas
- Electromagnetismo
- Ondas
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Incluye exámenes simulacro en tu rutina de estudio, de esa forma pondrás a prueba tus conocimientos en condiciones similares a la prueba real.
Las siguientes, son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve cada parte (I, II y III) por tu cuenta antes de checar las respuestas.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
Reactivo 1
Encuentre las coordenadas del vector o los vectores, que tienen una magnitud de 4 unidades, tiene como extremo al punto A\left(1, 1\right) y su ángulo respecto a la horizontal es de 60°.
- 3.58\widehat{i}+1.79\widehat{j}, -3.58\widehat{i}-1.79\widehat{j}
- -3.58\widehat{i}-1.79\widehat{j}
- 3.58\widehat{i}+1.79\widehat{j}
- \widehat{i}+\widehat{j}, -\widehat{i}-\widehat{j}
Solución:
Con esta mínima información que nos ofrece el enunciado, podemos comenzar por plantear la ecuación de magnitud de un vector en 2 dimensiones.
\left|\overrightarrow{v}\right|=\sqrt{{\left(1-x\right)}^{2}+{\left(1-y\right)}^{2}}\to {4}^{2}={\left(1-x\right)}^{2}+{\left(1-y\right)}^{2}
{\left(1-x\right)}^{2}+{\left(1-y\right)}^{2}=16
Esta ecuación resultante es similar a la de una circunferencia. Tenemos infinitos pares \left(x, y\right) que satisfacen la igualdad, el dato que nos permitirá obtener una solución finita es el ángulo respecto a la horizontal.
\mathrm{cos}60°=\frac{1-y}{1-x}
Sustituyendo \mathrm{cos}60°=\frac{1}{2} nos queda:
\frac{1}{2}=\frac{1-y}{1-x}
Despejamos.
1-x=2-2y\to 2y-x=1
Ahora tenemos 2 ecuaciones y 2 incógnitas. Despejando a la x nos queda:
x=2y-1
Sustituimos este resultado en la primera ecuación.
{\left(1-2y+1\right)}^{2}+{\left(1-y\right)}^{2}=16
Simplificamos y desarrollamos.
{\left(2-2y\right)}^{2}+{\left(1-y\right)}^{2}=16
4-8y+4{y}^{2}+1-2y+{y}^{2}=16
Agrupamos.
5{y}^{2}-10y-11=0
Resolviendo la ecuación de segundo grado.
{y}_{1}=2.79, {y}_{2}=-0.79
Sustituimos estos valores de y en x=2y-1 para obtener los valores de x .
{x}_{1}=2\left(2.79\right)-1=4.58
{x}_{2}=2\left(-0.79\right)-1=-2.58
Los puntos que cumplen la condición del enunciado son:
{P}_{1}\left(4.58, 2.79\right) y {P}_{2}\left(-2.58, -0.79\right)
Podemos comprobar gráficamente nuestro resultado:
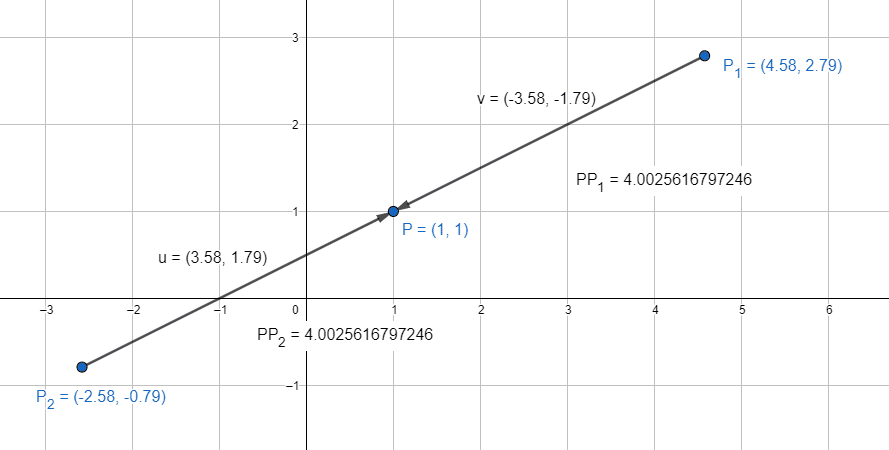
Las coordenadas de los dos vectores que cumplen con la condición se calculan como:
\overrightarrow{u}=\left(1+2.58\right)\widehat{i}+\left(1+0.79\right)\widehat{j}=3.58\widehat{i}+1.79\widehat{j}
\overrightarrow{v}=\left(1-4.58\right)\widehat{i}+\left(1-2.79\right)\widehat{j}=-3.58\widehat{i}-1.79\widehat{j}
Si analizamos el resultado, tiene lógica obtener dos soluciones posibles, porque sobre la recta que contiene al punto \left(1, 1\right) y que tiene pendiente de 60°, se pueden trazar dos segmentos dirigidos hacia \left(1, 1\right) tal como se muestra en la figura. Concluimos que la respuesta correcta es el inciso a).
Reactivo 2
Al realizar numerosos experimentos con una resistencia eléctrica de 5 \mathrm{\Omega } , se encontró que la relación entre la corriente y el voltaje aplicado es V=5I . ¿Cuál de las siguientes aseveraciones es correcta?
- V es inversamente proporcional a I
- R es directamente proporcional a I
- V es directamente proporcional a I
- I es una variable estocástica
Solución:
La ley física que se indica en el enunciado es la conocida Ley de Ohm y establece una relación directa entre la corriente y el voltaje aplicado sobre una resistencia R .
La expresión V=5I , nos dice que el voltaje en terminales de la resistencia de 5 \mathrm{\Omega } es directamente proporcional a la corriente que atraviesa al elemento. Dicho de otra manera, existe una relación lineal entre el voltaje y la corriente en una resistencia eléctrica.
Concluimos entonces que la respuesta correcta se encuentra en el inciso c).
Reactivo 3
Ordene de mayor a menor las siguientes cantidades expresadas en notación científica.
- 4\times {10}^{3}
- 5\times {10}^{-2}
- 2.3\times 10
- 3\times {10}^{4}
- 4, 2, 3, 1
- 1, 3, 4, 2
- 4, 1, 3, 2
- 4, 2, 3, 1
Solución:
Para ordenar las cantidades en notación científica primero debemos expresarlas, a todas, con el mismo exponente. Seleccionamos cualquier exponente, en este caso será el 3. La primera cantidad ya posee exponente 3, por lo que saltamos a la siguiente.
Para la segunda cantidad, debemos multiplicar y dividir por {10}^{5} .
\frac{5}{{10}^{5}}\times {10}^{-2}\times {10}^{5}=0.00005\times {10}^{3}
En la tercera cantidad, multiplicamos y dividimos por {10}^{3} .
\frac{2.3}{{10}^{2}}\times 10\times {10}^{2}=0.023\times {10}^{3}
Al contrario que las anteriores, para la cuarta cantidad multiplicamos y dividimos por un exponente negativo {10}^{-1} –
\frac{3}{{10}^{-1}}\times {10}^{4}\times {10}^{-1}=30\times {10}^{3}
Ahora que todos los incisos tienen el mismo exponente, solo nos queda comparar los factores de la izquierda.
30>4>0.023>0.00005
O, según el orden dado:
4>1>3>2
Comparando con las opciones, concluimos que la correcta está en la c).
Reactivo 4
Calcule las componentes de un vector que apunta hacia el noroeste, con magnitud es de 5 unidades y un ángulo respecto a la horizontal de 30°.
- -4.33\widehat{i}-2.5\widehat{j}
- -4.33\widehat{i}+2.5\widehat{j}
- 4.33\widehat{i}-2.5\widehat{j}
- 4.33\widehat{i}+2.5\widehat{j}
Solución:
A partir de los datos del enunciado, podemos dibujar el vector tal como se muestra en la figura.
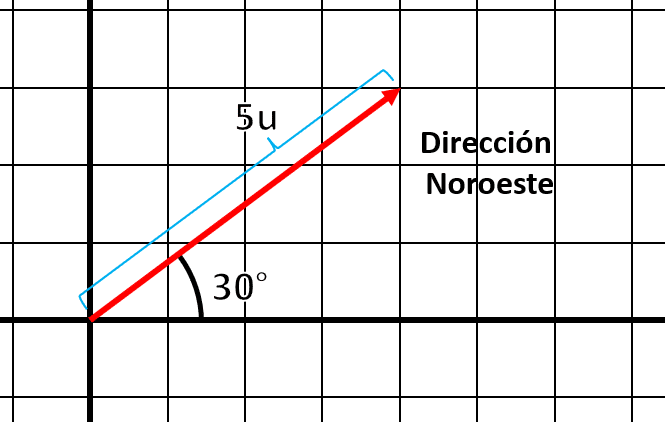
Para encontrar sus componentes, simplemente aplicamos las identidades trigonométricas del seno y el coseno.
{v}_{x}=5\mathrm{cos}30°
{v}_{y}=5\mathrm{sin}30°
Sustituyendo el valor de cada identidad y teniendo en cuenta que solo nos interesa la solución que apunta hacia el noroeste, nos queda:
\overrightarrow{v}=4.33\widehat{i}+2.5\widehat{j}
Comparando con los incisos, la respuesta correcta es el d).
Reactivo 5
Una fuerza de magnitud igual a 50 N actúa sobre un cuerpo con un ángulo de 30° respecto a la horizontal en dirección noroeste mientras que otra, también de 50 N pero con ángulo de 150° respecto a la horizontal, apunta hacia el noreste y también actúa sobre el cuerpo.
Calcule las componentes de la fuerza resultante.
Solución:
Antes de comenzar a calcular las componentes de la resultante, vamos a plasmar sobre el plano los vectores indicados por el enunciado.
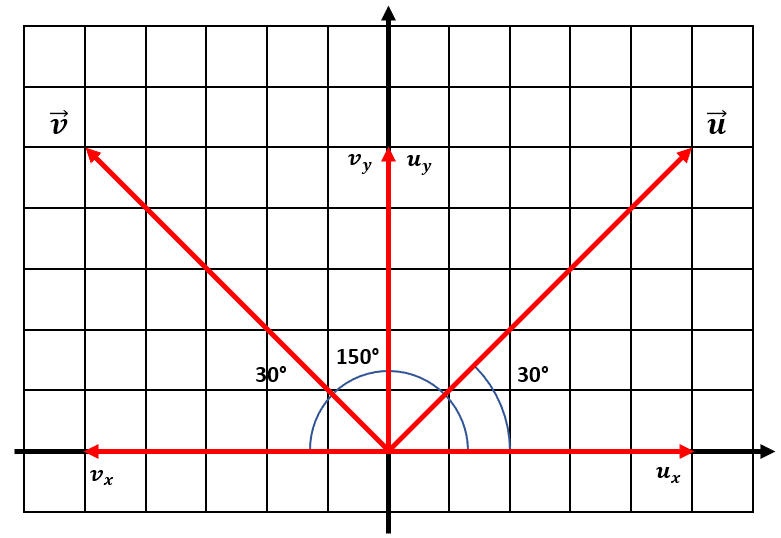
Si analizamos un poco la imagen, nos daremos cuenta de que las componentes {v}_{x} y {u}_{x} tienen la misma magnitud debido al ángulo de 30° en ambos vectores y que ambos miden 50 unidades, pero con signos opuestos, es decir, se cancelan mutuamente.
Con esta simplificación que hemos hecho a partir de analizar la figura, solo nos queda calcular las componentes verticales, las cuales apuntan en la misma dirección, es decir, se suman y son iguales en magnitud.
{v}_{y}={u}_{y}=50\mathrm{sin}30°=25
La resultante se calcula como:
\overrightarrow{u}+\overrightarrow{v}={u}_{x}-{v}_{x}+{u}_{y}+{v}_{y}=25\widehat{j}+25\widehat{j}=50\widehat{j}
Las componentes de la fuerza resultante son:
\overrightarrow{w}=0\widehat{i}+50\widehat{j}
Comparando con las opciones, concluimos que la respuesta correcta está en b).
Reactivo 6
A partir de la siguiente tabla, complete correctamente los espacios en blanco.

- 2\times {10}^{-3} \mathrm{k}\mathrm{g},\mathrm{ }0.00966\mathrm{ }\mathrm{A},\mathrm{ }9.2\times {10}^{-4} \mathrm{s}
- 2\times {10}^{4} \mathrm{k}\mathrm{g},\mathrm{ }0.000966\mathrm{ }\mathrm{A},\mathrm{ }9.2\times {10}^{3} \mathrm{s}
- 2\times {10}^{-4} \mathrm{k}\mathrm{g},\mathrm{ }0.000966\mathrm{ }\mathrm{A},\mathrm{ }9.2\times {10}^{-3} \mathrm{s}
- 2\times {10}^{-5} \mathrm{k}\mathrm{g},\mathrm{ }0.0000966\mathrm{ }\mathrm{A},\mathrm{ }9.2\times {10}^{-4} \mathrm{s}
Solución:
En este caso, debemos rellenar los cuadros con la cantidad expresada en notación científica o con la medición original antes de ser transformada. Comenzamos por la primera fila, pasando a notación científica.
Corremos el punto decimal 4 lugares hacia la derecha.
0.0002 \mathrm{k}\mathrm{g}=2\times {10}^{-4} \mathrm{k}\mathrm{g}
En la segunda fila, debemos dividir la cantidad por {10}^{4} .
9.66\times {10}^{-4} \mathrm{A}=\frac{9.66}{{10}^{4}} \mathrm{A}=0.000966\mathrm{ }\mathrm{A}
Finalmente, para la tercera fila corremos la coma hacia la derecha 3 veces, con el exponente negativo.
0.0092 \mathrm{s}=9.2\times {10}^{-3} \mathrm{s}
Rellenando la tabla nos queda:
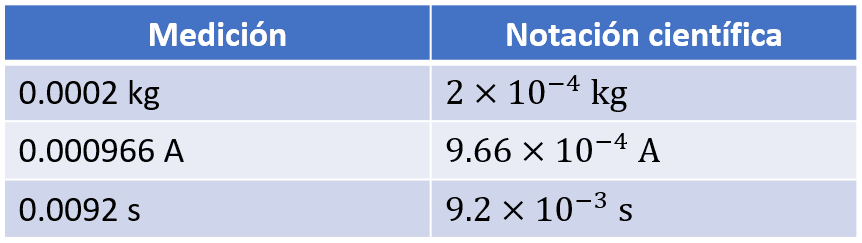
Comparando con los incisos, la respuesta correcta es la c).
Reactivo 7
Se dice que un instrumento de medición es preciso cuando…
- Existe gran proximidad entre el resultado obtenido y un valor de referencia
- Existe gran proximidad entre un conjunto de mediciones hechas bajo las mismas circunstancias
- Es también exacto
- Es ideal
Solución:
Cuando realizamos mediciones con instrumentos, existe un conjunto de parámetros que pueden indicarnos si el mismo es o no adecuado para las condiciones del experimento y, entre ellas, se encuentran la precisión y la exactitud.
La precisión hace alusión a la proximidad entre un conjunto de mediciones realizadas bajo las mismas circunstancias y que tienen el mismo valor de referencia.
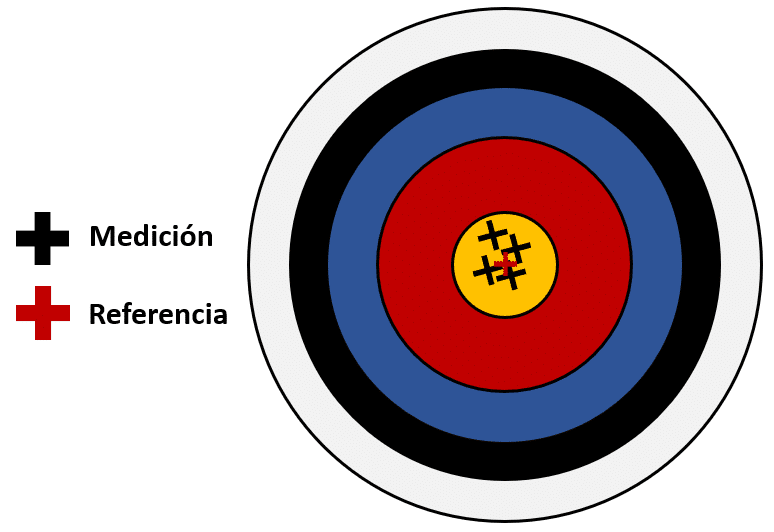
Por otro lado, la exactitud se refiere a la cercanía que tiene una medición hecha con el instrumento respecto a un valor tomado como referencia. Viendo la imagen anterior, podemos decir que el instrumento es preciso por la cercanía entre las 4 mediciones, pero también exacto, porque las 4 se encuentran muy cercanas al valor de referencia.
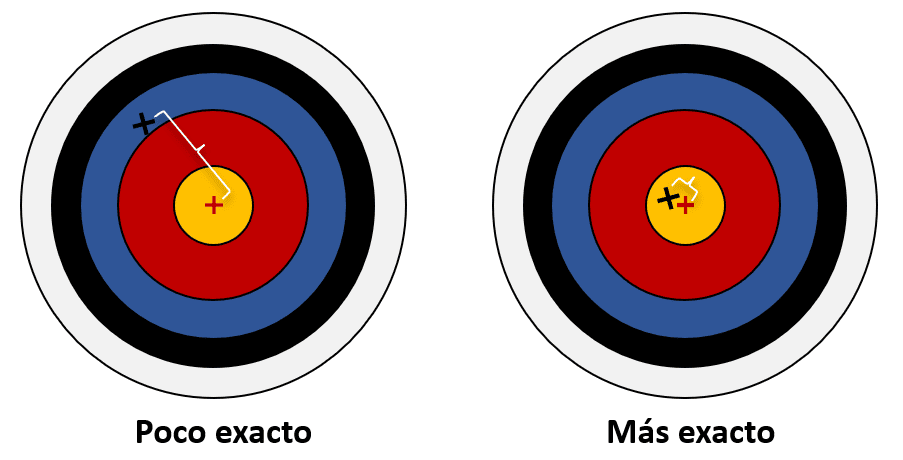
Concluimos que la respuesta correcta es el inciso b).
Reactivo 8
Dados los vectores \overrightarrow{u}=i+3j-2k y \overrightarrow{v}=2i+4j-k , determinar el ángulo que forman entre sí.
- 11.07°
- 21.07°
- 31.07°
- 41.07°
Solución:
Para calcular el ángulo entre dos vectores, podemos emplear tanto el producto escalar como el producto vectorial, pero, debido a que calcular el producto cruz es más complejo, vamos a realizar la estimación a partir de la definición de producto punto.
Producto punto entre dos vectores.
\overrightarrow{u}\cdot \overrightarrow{v}={u}_{x}{v}_{x}+{u}_{y}{v}_{y}+{u}_{z}{v}_{z}=\left|\overrightarrow{u}\right|\left|\overrightarrow{v}\right|\mathrm{cos}\alpha
Calculamos la parte izquierda de la igualdad.
{u}_{x}{v}_{x}+{u}_{y}{v}_{y}+{u}_{z}{v}_{z}=\left(1\right)\left(2\right)+\left(3\right)\left(4\right)+\left(-2\right)\left(-1\right)=16
Ahora, vamos a calcular los módulos de los vectores.
\left|\overrightarrow{u}\right|=\sqrt{{1}^{2}+{3}^{2}+{\left(-2\right)}^{2}}=\sqrt{14}
\left|\overrightarrow{v}\right|=\sqrt{{2}^{2}+{4}^{2}+{\left(-1\right)}^{2}}=\sqrt{21}
Despejamos el ángulo y sustituimos los valores.
\mathrm{cos}\alpha =\frac{{u}_{x}{v}_{x}+{u}_{y}{v}_{y}+{u}_{z}{v}_{z}}{\left|\overrightarrow{u}\right|\left|\overrightarrow{v}\right|}=\frac{16}{\sqrt{294}}
\alpha =21.07°
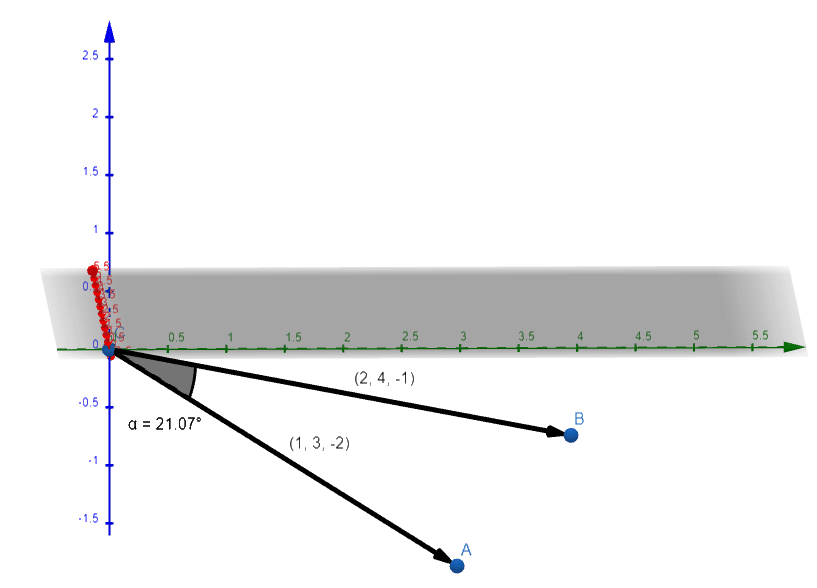
El ángulo entre los vectores es de 21.07°.
La respuesta correcta es el inciso b).
Reactivo 9
Calcule el valor de k para que los vectores \overrightarrow{u}=\left(2, k, 1\right) y \overrightarrow{v}=\left(4, -2, -2\right) para que sean perpendiculares (que el ángulo entre ellos sea 90°).
- 2
- 3
- 4
- 5
Solución:
Para determinar el valor de k que cumple la condición impuesta por el enunciado, podemos utilizar el producto escalar entre dos vectores ya que, por definición, este es nulo (igual a cero) cuando los vectores son perpendiculares.
\mathrm{S}\mathrm{i}\mathrm{ }\overrightarrow{u} \mathrm{y}\mathrm{ }\overrightarrow{v} \mathrm{s}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{ }\to \mathrm{ }\overrightarrow{u}\cdot \overrightarrow{v}=0
Aplicando la definición de producto punto.
{u}_{x}{v}_{x}+{u}_{y}{v}_{y}+{u}_{z}{v}_{z}=0\to \left(2\right)\left(4\right)+\left(k\right)\left(-2\right)+\left(1\right)\left(-2\right)=0
8-2k-2=0\to 2k=6
\therefore k=3
Para que los vectores sean perpendiculares, la coordenada k debe ser igual a 3.
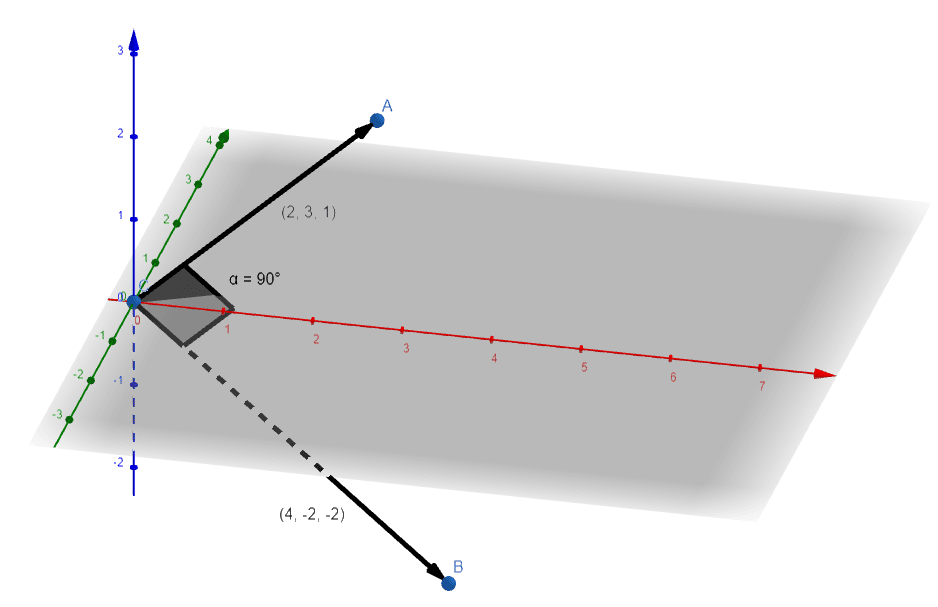
Concluimos que la respuesta correcta es la b).
Reactivo 10
Calcule el grosor que tendría una pared recién pintada con un galón de pintura de 5\times {10}^{-3} {\mathrm{m}}^{3} , si la pared en cuestión tiene una superficie de 30 {\mathrm{m}}^{2} .
- 166 mm
- 16.6 mm
- 1.66 mm
- 0.166 mm
Solución:
Para calcular el grosor que tendría la capa de pintura, debemos recurrir a la ecuación de volumen.
v=x\cdot y\cdot z
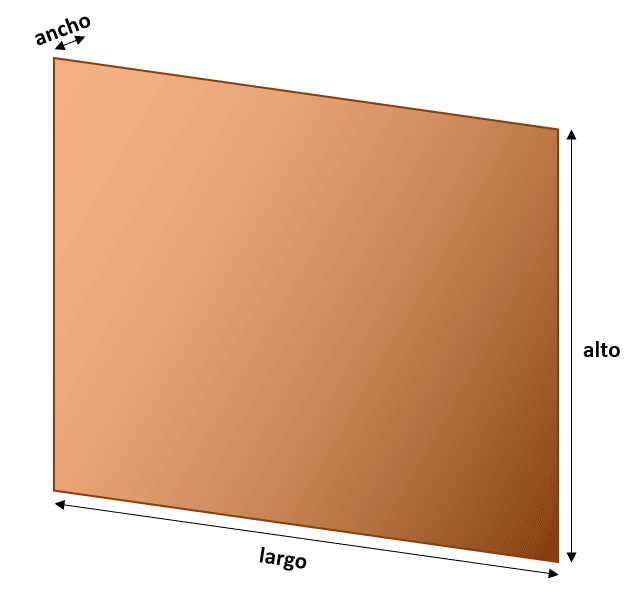
Donde x , y y z son el largo, el ancho y la altura respectivamente. Debido a que el galón se utiliza por completo, la ecuación de volumen se iguala al volumen del galón.
x\cdot y\cdot z=5\times {10}^{-3}
Si vemos la pared desde una perspectiva frontal, la superficie corresponde al producto del largo y la altura 30 {\mathrm{m}}^{2}=x\cdot z .
30\cdot y=5\times {10}^{-3}
Despejamos el ancho correspondiente al grosor.
y=\frac{5\times {10}^{-3}}{30}=1.66\times {10}^{-4} \mathrm{m}=0.166 \mathrm{m}\mathrm{m}
El grosor de la capa de pintura es aproximadamente de 0.166 milímetros.
Concluimos que la respuesta correcta es el inciso d).


