Examen Simulacro IPN IyCFM de Matemáticas | Parte 3

Vamos con los reactivos del 21 al 30, para esta tercera parte del examen simulador de matemáticas del IPN, es importante que consultes la demanda que tiene tu carrera, ya que en el área de ingeniería y ciencias físico matemáticas existen programas que aceptan a muy pocos aspirantes.

Sigue practicando e identificando los temas que más se te dificultan. Recuerda contar con un plan de acción en cada tema que se haga muy difícil.

Reactivo 21

Ordene las siguientes funciones, de mayor a menor, de acuerdo al valor de su derivada en el punto x=1 .

1. f\left(x\right)=4{x}^{2}-1
2. g\left(x\right)=\frac{1}{2}{x}^{3}+2{x}^{2}
3. h\left(x\right)=1-3x
4. y\left(x\right)={x}^{4}-{x}^{3}

 

1. 1, 2, 3, 4
2. 2, 1, 3, 4
3. 4, 3, 1, 2
4. 1, 2, 4, 3

Solución:

Resolver este problema será bastante sencillo, primero debemos encontrar la derivada de cada una de las funciones, luego evaluarlas en el punto dado y finalmente ordenarlas de mayor a menor, de acuerdo al valor obtenido.

Derivada de f\left(x\right) .

{f}^{\text{'}}\left(x\right)={\left(4{x}^{2}-1\right)}^{\text{'}}=8x

Derivada de g\left(x\right) .

{g}^{\text{'}}\left(x\right)={\left(\frac{1}{2}{x}^{3}+2{x}^{2}\right)}^{\text{'}}=\frac{3}{2}{x}^{2}+4x

Derivada de h\left(x\right) .

{h}^{\text{'}}\left(x\right)={\left(1-3x\right)}^{\text{'}}=-3

Derivada de y\left(x\right) .

{y}^{\text{'}}\left(x\right)={\left({x}^{4}-{x}^{3}\right)}^{\text{'}}=4{x}^{3}-3{x}^{2}

Ahora, sustituimos el valor dado x=1 .

{f}^{\text{'}}\left(1\right)=8

{g}^{\text{'}}\left(1\right)=\frac{3}{2}+4=\frac{11}{2}

{h}^{\text{'}}\left(1\right)=-3

{y}^{\text{'}}\left(1\right)=1

Ordenando de mayor a menor:

f, g, y, h\to 1, 2, 4, 3

Comparando con las opciones, indicamos como correcta la d).

Reactivo 22

Calcule el dominio de la siguiente función.

f\left(x\right)=\frac{\sqrt{x-1}}{x+1}

1. \left[1, \infty \right)
2. \left[-1, \infty \right)
3. \left[0, \infty \right)
4. \left(1, \infty \right)

Solución:

Estudiar el dominio de una función real, corresponde a obtener el conjunto de valores de x para los cuales, existe y es acotada. Cada tipo de función elemental tiene sus propias restricciones, de tal forma que una función compuesta por varias funciones elementales tiene su dominio en la intersección de las soluciones de dichas elementales.

Para f\left(x\right) identificamos dos funciones elementales: una racional, ya que principalmente se trata de una función racional y cuya restricción es que el denominador sea distinto de cero y en el denominador tenemos una función radical que, debido a que su índice es par, la restricción es que el radicando sea mayor o igual que cero.

Comenzamos con la función racional.

{\mathrm{D}\mathrm{o}\mathrm{m}}_{1}\left\{x+1\ne 0\right\}

Resolvemos la restricción.

x+1\ne 0\to x\ne -1

La restricción de la primera función es: {\mathrm{D}\mathrm{o}\mathrm{m}}_{1}=x\in R-\left\{-1\right\}

Vamos con la función radical.

{\mathrm{D}\mathrm{o}\mathrm{m}}_{2}\left\{x-1\ge 0\right\}

Resolvemos la inecuación.

x-1\ge 0\to x-1\ge 0

x\ge 1

La restricción de la segunda función es: {\mathrm{D}\mathrm{o}\mathrm{m}}_{2}=x\in \left[1, \infty \right) .

Interceptamos ambos conjuntos:

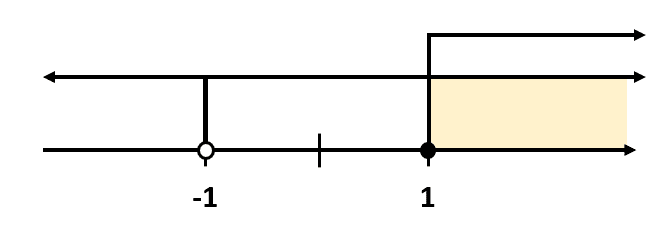
El dominio de f\left(x\right) son todos los reales mayores o iguales que 1.

\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=x\in \left[1, \infty \right)

Concluimos indicando como correcta la opción a).

Reactivo 23

Obtenga el valor de f\left(x\right)=\left\{\begin{array}{c}{x}^{2}+2 si x<1\\ x-2 si x>1\end{array}\right. cuando x=1

1. 0
2. 3
3. No está definido
4. 1

Solución:

Para estudiar funciones a trozos, debemos identificar qué funciones actúan en determinados intervalos de x . Por ejemplo, en la función del enunciado entre \left(-\infty , 1\right) actúa la función {x}^{2}+2 pero sin incluir al 1, es decir, que no podemos obtener imagen para x=1 con esta parte de la función.

Podemos dibujar a la función de la siguiente forma:

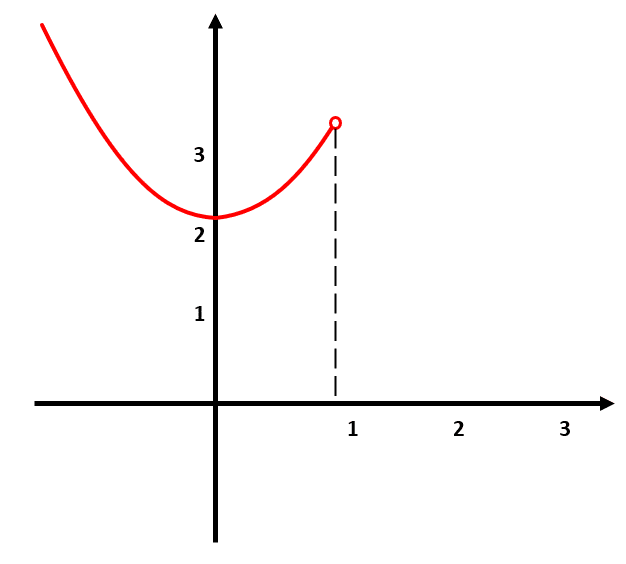
Ahora, con el segundo tramo de la función obtenemos las imágenes para x>1 pero tampoco podemos calcular una imagen para x=1 ya que no está definida en dicho punto. El segundo tramo se puede graficar de la siguiente forma:

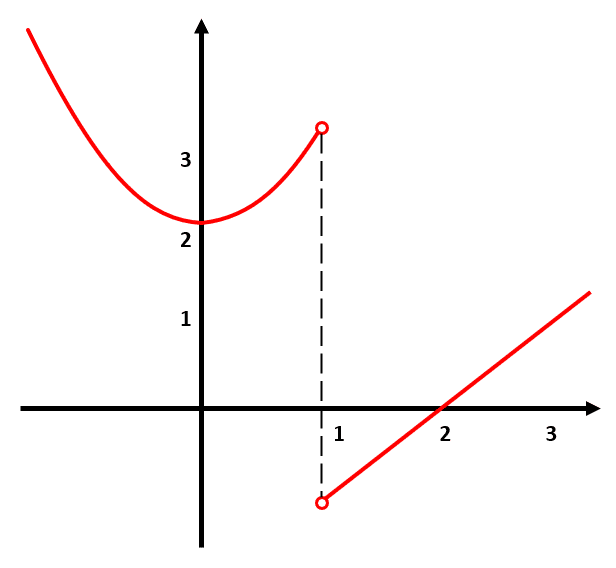
Los puntos con relleno blanco indican que la función no tiene imagen allí.

Ya que ninguno de los tramos de la función se encuentra definido para x=1 , concluimos entonces que f\left(x\right) no está definida en x=1 . La respuesta correcta es el inciso c).

Reactivo 24

Determine el intervalo de la siguiente desigualdad.

x+1\ge 3

1. \left[2, \infty \right)
2. \left(2, \infty \right)
3. \left[-2, \infty \right)
4. \left(-2, \infty \right)

Solución:

Para encontrar el conjunto solución de la inecuación, debemos dejar sola a la x en el miembro de la izquierda, para ello, restamos 1 en ambos lados.

x+1-1\ge 3-1\to x\ge 2

Todos los números mayores o iguales que 2 satisfacen la desigualdad. Expresado en notación de conjunto:

x\in \left[2, \infty \right)

Comparando con las opciones, indicamos como respuesta correcta la a).

Reactivo 25

Calcule la derivada de la función f\left(x\right)=\frac{1}{2\sqrt[3]{x+1}} .

1. -\frac{1}{3}\cdot \frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}
2. \frac{1}{6}\cdot \frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}
3. -\frac{1}{6}\cdot \frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}
4. -\frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}

Solución:

A simple vista, podríamos pensar que la fórmula para derivar es la del cociente de dos funciones, pero podemos simplificar separando como constante al \frac{1}{2} y aplicando la propiedad de las potencias del exponente negativo.

f\left(x\right)=\frac{1}{2}\cdot \frac{1}{\sqrt[3]{x+1}}=\frac{1}{2}\cdot \frac{1}{{\left(x+1\right)}^{\frac{1}{3}}}=\frac{1}{2}\cdot {\left(x+1\right)}^{-\frac{1}{3}}

Ahora podemos aplicar la fórmula de la derivada de una potencia, la cuál es más sencilla.

{f}^{\text{'}}\left(x\right)=\frac{1}{2}\cdot {\left[{\left(x+1\right)}^{-\frac{1}{3}}\right]}^{\text{'}}=\frac{1}{2}\cdot \left[-\frac{1}{3}{\left(x+1\right)}^{-\frac{4}{3}}\cdot {\left(x+1\right)}^{\text{'}}\right]=-\frac{1}{6}\cdot \frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}

Finalmente:

{f}^{\text{'}}\left(x\right)=-\frac{1}{6}\cdot \frac{1}{\sqrt[3]{{\left(x+1\right)}^{4}}}

Comparando con los incisos, la respuesta correcta es la c).

Reactivo 26

Encuentre la familia de circunferencias centradas en el punto \left(1, 1\right) .

1. {\left(x+1\right)}^{2}+{\left(y-1\right)}^{2}={r}^{2}
2. {\left(x-1\right)}^{2}+{\left(y+1\right)}^{2}={r}^{2}
3. {\left(x+1\right)}^{2}+{\left(y+1\right)}^{2}={r}^{2}
4. {\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}={r}^{2}

Solución:

Recordemos que para obtener la ecuación de cualquier circunferencia solo necesitamos dos elementos: un centro y su radio.

{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}

En este caso, el enunciado nos dice que la familia de circunferencias debe estar centrada en \left(1, 1\right) por tanto, el parámetro que describe a las infinitas circunferencias que pertenecen a la familia. Solo debemos sustituir el centro en la ecuación ordinaria para encontrar la expresión analítica de la familia.

{C}_{f}: {\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}={r}^{2}

Comparando con las opciones, indicamos correcta la d).

Reactivo 27

Encuentre las coordenadas del centro de la elipse dada por la siguiente ecuación:

{x}^{2}+4{y}^{2}-2x-8y=11

1. \left(1, 1\right)
2. \left(-1, 1\right)
3. \left(1, -1\right)
4. \left(-1, -1\right)

Solución:

Para encontrar las coordenadas del centro de la elipse, será necesario aplicar competición de cuadrados, de esta forma obtendremos dos términos de la forma {\left(x-a\right)}^{2} y {\left(y-b\right)}^{2} donde a y b serán las coordenadas del centro.

Empecemos a completar cuadrado para la x . Agrupamos los términos con x .

{x}^{2}-2x+4{y}^{2}-8y=11

El término a la 1 de la x nos indica que a en {\left(x-a\right)}^{2} debe ser 1. Por tanto, sumamos y restamos 1.

{x}^{2}-2x+1-1+4{y}^{2}-8y=11

Ahora, el conjunto de términos {x}^{2}-2x+1 corresponde con el desarrollo de {\left(x-1\right)}^{2} .

{\left(x-1\right)}^{2}-1+4{y}^{2}-8y=11

Para la y primero extraemos factor común el 4.

{\left(x-1\right)}^{2}-1+4\left({y}^{2}-2y\right)=11

Nos queda el mismo caso que para la x , por tanto, sumamos y restamos 1.

{\left(x-1\right)}^{2}+4\left({y}^{2}-2y+1-1\right)=11+1

Completamos cuadrado para {y}^{2}-2y+1 como {\left(y-1\right)}^{2} .

{\left(x-1\right)}^{2}+4\left[{\left(y-1\right)}^{2}-1\right]=12

{\left(x-1\right)}^{2}+4{\left(y-1\right)}^{2}-4=12

Podríamos terminar de despejar, pero solo nos interesan las coordenadas del centro, por tanto:

C\left(1, 1\right)

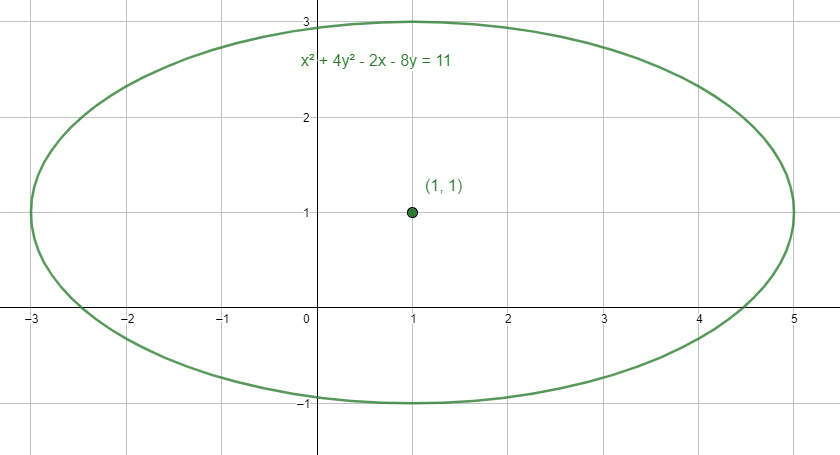
Concluimos indicando como respuesta correcta la a).

Reactivo 28

Determine las coordenadas del vértice de la parábola cuya ecuación general es:

y=-8{x}^{2}-32x-28

1. \left(-2, 4\right)
2. \left(2, -4\right)
3. \left(2, 4\right)
4. \left(-2, -4\right)

Solución:

Para encontrar las coordenadas del vértice de la parábola, es necesario completar cuadrados respecto a la variable x . Comenzamos extrayendo factor común -8.

y=-8\left({x}^{2}+4x+\frac{7}{2}\right)

Para que podamos aplicar el producto notable {\left(a+b\right)}^{2}={a}^{2}+2ab+{b}^{2} , es necesario sumar y restar {b}^{2} . En nuestro caso b=2 por tanto, hay que sumar y restar 4.

y=-8\left({x}^{2}+4x+4-4+\frac{7}{2}\right)

Aplicamos {\left(x+2\right)}^{2}={x}^{2}+4x+4 en sentido inverso.

y=-8\left[{\left(x+2\right)}^{2}-\frac{1}{2}\right]

Desarrollamos la distributiva.

y=-8{\left(x+2\right)}^{2}+4

Pasamos el 4 al otro lado.

y-4=-8{\left(x+2\right)}^{2}

Con esta expresión concluimos que las coordenadas del vértice son:

V\left(-2, 4\right)

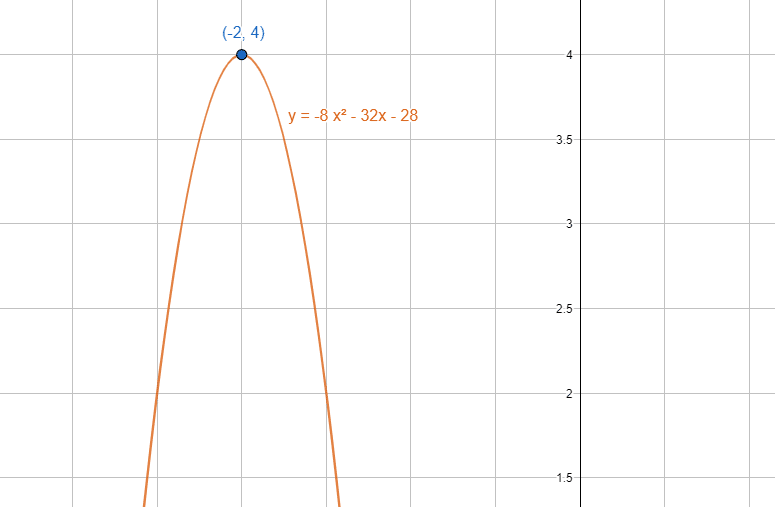
Comparando con las opciones, concluimos indicando la a) como correcta.

Reactivo 29

Calcule el radio de la circunferencia que tiene como extremos en el diámetro los puntos \left(0, -2\right) y \left(0, 4\right) .

1. 4
2. 2
3. 6
4. 3

Solución:

Debido a que el diámetro mide el doble que el radio, debemos calcular la distancia entre los puntos y luego dividirla entre 2.

D=\sqrt{{\left(0-0\right)}^{2}+{\left(-2-4\right)}^{2}}=6

El radio se calcula como:

r=\frac{D}{2}=3

La respuesta correcta se encuentra en el inciso d).

Reactivo 30

¿Cuál de los siguientes enunciados describe el lugar geométrico de una circunferencia?

1. Es el conjunto de puntos que distan igual respecto a dos puntos fijos
2. Es el conjunto de puntos que distan de dos puntos fijos más que la distancia entre los puntos
3. Es el conjunto de puntos que distan igual respecto a un punto fijo
4. Es el conjunto de punto que distan más que un segmento dado

Solución:

En este caso, debemos simplemente recordar la definición geométrica de circunferencia:

Es el conjunto de puntos en el plano que distan igual respecto a un punto fijo llamado centro.

Teniendo en cuenta esto y examinando los enunciados, queda claro que la respuesta correcta es la c).