¡Muy bien aspirante! Llegamos a la quinta y última parte del simulacro de física para el área de CSyA del Instituto Politécnico Nacional.

Lee con detalle cada enunciado, analiza los datos e identifica las leyes físicas que te permitirán encontrar la solución a los problemas. Además, no dejes de prepararte para presentar el examen de ingreso a la carrera de tus sueños.
Reactivo 41
Dado el circuito resistivo que se muestra en la figura, calcule la corriente dada por la fuente de alimentación. Tenga en cuenta {R}_{1}={R}_{3}=1 \mathrm{\Omega } y {R}_{2}={R}_{4}=2 \mathrm{\Omega } .
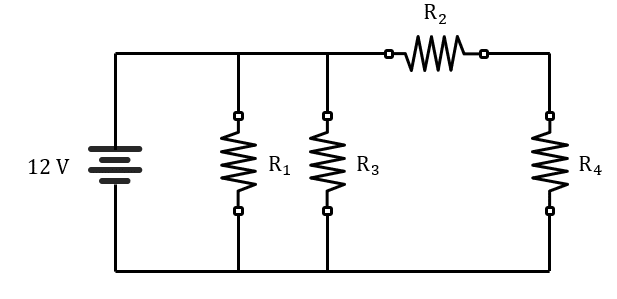
- 12 A
- 3 A
- 33 A
- 24 A
Solución:
Aunque el circuito de la figura parezca complejo, podemos simplificar el cálculo de la corriente de la fuente aplicando los teoremas de resistencias en serie y en paralelo hasta obtener una única resistencia conectada a la fuente y, finalmente, aplicar la ley de Ohm para obtener el valor de la corriente.
Inspeccionando el circuito, vemos que las resistencias {R}_{2} y {R}_{4} se encuentran en serie, por tanto:
{R}_{24}={R}_{2}+{R}_{4}=2+2=4 \mathrm{\Omega }
El circuito quedaría:
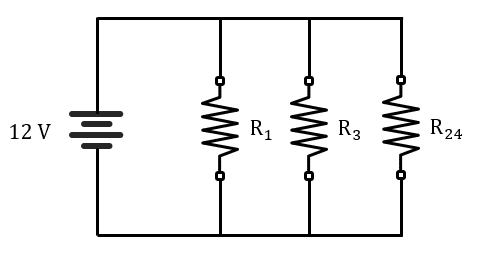
Aplicamos resistencias en paralelo para {R}_{1} y {R}_{3} .
{R}_{13}=\frac{{R}_{1}{R}_{3}}{{R}_{1}+{R}_{3}}=\frac{\left(1\right)\left(1\right)}{1+1}=0.5 \mathrm{\Omega }
Sustituyendo en el circuito nos queda:
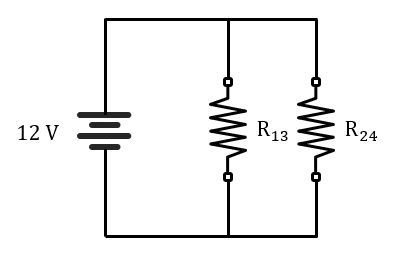
Por último, aplicamos resistencias en paralelo entre {R}_{13} y {R}_{24} .
R=\frac{{R}_{13}{R}_{24}}{{R}_{13}+{R}_{24}}=\frac{\left(0.5\right)\left(4\right)}{0.5+4}=0.44 \mathrm{\Omega }
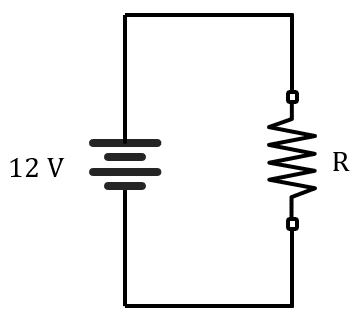
A partir de la ley de Ohm, obtenemos que la corriente de la fuente es:
I=\frac{12}{R}=\frac{12}{0.44}=27.27 \mathrm{A}
La fuente de alimentación otorga 27.27 Amperios de corriente al circuito.
Concluimos que la respuesta correcta se encuentra en el inciso b).
Reactivo 42
Para la práctica final del laboratorio de física, el profesor ha escondido en una caja totalmente cerrada un circuito resistivo puro cuya configuración es totalmente desconocida para los estudiantes.
La caja lo único que muestra son dos bornes de conexión y en la mesa del laboratorio hay un amperímetro y una fuente de alimentación regulable.
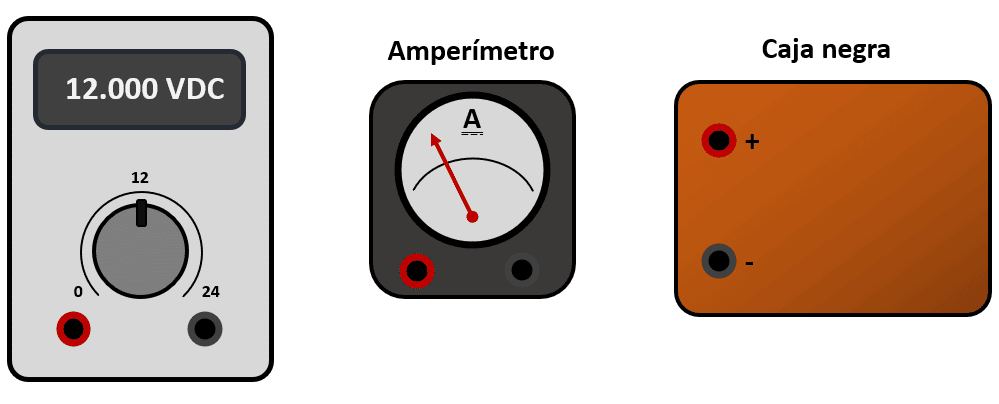
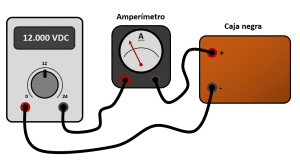
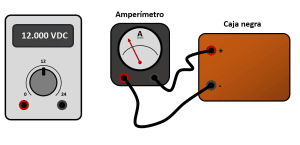
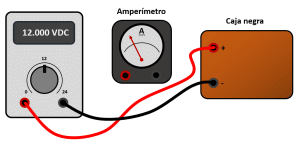
Indique cuál de los siguientes diagramas de conexión permitiría a los estudiantes conocer la resistencia equivalente de la “caja negra”.
Solución:
En este caso, la única forma que tienen los estudiantes para medir la resistencia equivalente de la “caja negra” es aplicando la ley de Ohm.
R=\frac{V}{I}
Es decir, con la fuente de alimentación debemos ingresar un voltaje conocido V a los terminales de la caja y con el amperímetro de aguja, medimos la intensidad de corriente I que consume el arreglo desconocido, para finalmente sustituirlo en la ecuación de la ley de Ohm.
La fuente de alimentación en la imagen del enunciado indica 12 V, el terminal positivo es el rojo y el negativo el de color negro. El amperímetro se conecta de la siguiente forma: la corriente debe entrar por el terminal positivo (rojo) y salir por el negativo. El terminal positivo de la caja negra es el indicado como rojo.
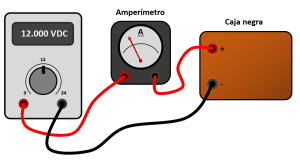
Cableamos esto de la siguiente forma:
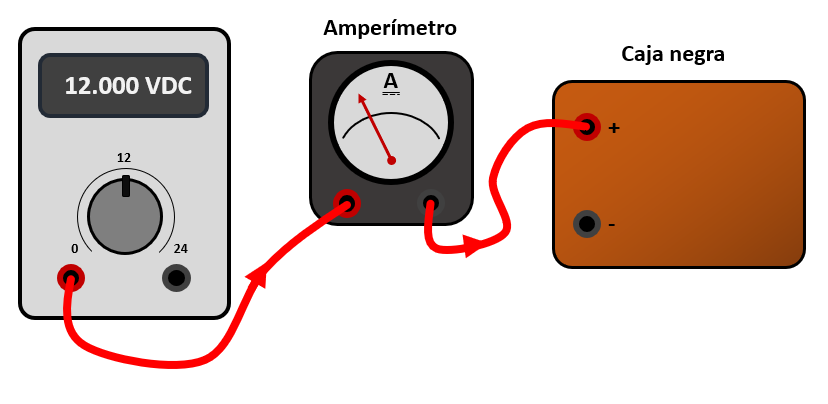
Ahora, la corriente que atraviesa el arreglo de la caja negra sale por el terminal negativo y llega al terminal negro de la fuente de alimentación.
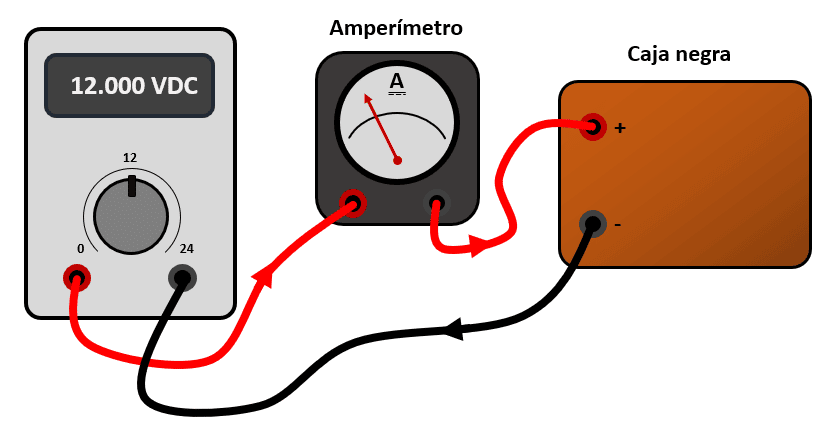
Con esta conexión, los estudiantes pueden estimar la resistencia equivalente de la caja negra.
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 43
Calcule el máximo voltaje al que puede ser conectado un equipo eléctrico con una potencia de consumo segura de 2500 W a una corriente de 20 A.
- 120 V
- 125 V
- 140 V
- 220 V
Solución:
En este caso, debemos utilizar la ecuación de potencia eléctrica para resolver el problema.
P=V\cdot I
Despejamos la tensión de la ecuación.
V=\frac{P}{I}
Ahora, ¿qué valores de potencia y corriente debemos sustituir? Si queremos conocer el máximo voltaje, debemos sustituir la máxima potencia que, en este caso, se nos indica como potencia segura y la máxima corriente, que serían los 20 Amperios de consumo a dicha potencia.
V=\frac{2500 \mathrm{W}}{20 \mathrm{A}}=125 \mathrm{V}
El equipo eléctrico soporta un voltaje máximo de 125 V.
La respuesta correcta es el inciso b).
Reactivo 44
Relacione los conceptos del electromagnetismo que se indican con los modelos matemáticos de forma correspondiente.

- 1A, 2D, 3B, 4C
- 1A, 2B, 3D, 4C
- 1A, 2D, 3C, 4B
- 1D, 2A, 3B, 4C
Solución:
Vamos a recordar brevemente cada uno de los conceptos, para luego relacionarlo con su modelo matemático correspondiente.
Ley de Faraday.
La fuerza electromotriz inducida en los terminales de una espira de alambre es directamente proporcional a la variación del flujo magnético respecto del tiempo.
\epsilon =\frac{d\mathrm{\Phi }}{dt}
1A.
Ley de Coulomb.
Establece que la magnitud de la fuerza eléctrica entre dos cargas eléctricas, es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.
F=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}^{2}}
2D.
Flujo magnético.
Es una cantidad escalar que nos permite medir la cantidad de líneas de campo magnético que atraviesan determinada superficie.
\mathrm{\Phi }=A\cdot B
3B.
Condensadores en paralelo.
Al conectar dos o más condensadores en paralelo, el voltaje del arreglo total es el mismo aplicado para cada condensador, pero la carga eléctrica total es la suma de las cargas de cada condensador.
C=\frac{1}{V}\sum {q}_{i}=\frac{\sum {q}_{i}}{V}=\sum {C}_{i}
4C.
Uniendo las respuestas parciales nos queda:
1A, 2D, 3B, 4C.
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 45
Las cargas eléctricas que se ________ en una dirección producen campos magnéticos _________.
- Desplazan – variables
- Dispersan – estacionarios
- Desplazan – estacionarios
- Dispersan – estacionarios
Solución:
A partir de los primeros experimentos de Oersted, sabemos que las cargas eléctricas que circulan a través de un conductor que cierra un circuito con una batería, producen un campo magnético estacionario, circular y centrado en el conductor, cuya intensidad decae a medida que nos alejamos del cable.
Teniendo en cuenta esto y examinando los incisos, queda en evidencia que las palabras que completan la frase son: desplazan y estacionarios.
Las cargas eléctricas que se desplazan en una dirección producen campos magnéticos estacionarios.
Concluimos que la respuesta correcta es la c).
Reactivo 46
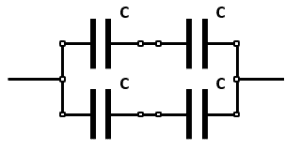
A partir de las siguientes configuraciones de capacitores, indique cuál de ellas tiene la mayor capacitancia equivalente entre sus terminales.
Solución:
Para encontrar el arreglo con la mayor capacidad equivalente, debemos aplicar las leyes de capacitores en serie y paralelo, comparar los resultados y seleccionar el más alto. Ten en cuenta que no se indica el valor de C , así que trabajaremos de forma netamente algebraica.
Capacitores en paralelo.
C=\sum {C}_{i}
Capacitores en serie.
C=\frac{1}{\sum \frac{1}{{C}_{i}}}
Primer arreglo.
Aplicamos capacitores en serie para ambas ramas y al resultado de ambos capacitores en paralelo.
{C}_{1}=\frac{C\cdot C}{C+C}+\frac{C\cdot C}{C+C}=\frac{C}{2}+\frac{C}{2}=C
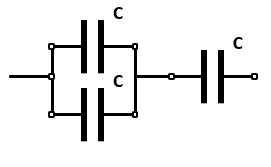
Segundo arreglo.
Resolvemos el paralelo y luego aplicamos serie del resultado con C .
{C}_{2}=\frac{\left(C+C\right)\cdot C}{\left(C+C\right)+C}=\frac{2}{3}C
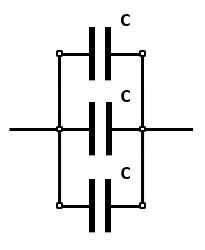
Tercer arreglo.
Debido a que los tres capacitores se encuentran en paralelo, el equivalente será la suma de las tres capacidades.
{C}_{3}=3C
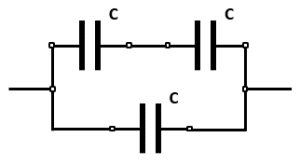
Cuarto arreglo.
Resolvemos la serie y luego el paralelo.
{C}_{4}=\frac{C\cdot C}{C+C}+C=\frac{C}{2}+C=\frac{3}{2}C
Finalmente:
{C}_{1}=C, {C}_{2}=\frac{2}{3}C, {C}_{3}=3C, {C}_{4}=\frac{3}{2}C
Comparando, concluimos que el arreglo del inciso c) tiene la mayor capacidad equivalente.
Reactivo 47
En la reflexión de la luz, el ángulo de incidencia es ______ que el ángulo de reflexión de la luz.
- El doble
- La mitad
- Igual
- Mayor
Solución:
En óptica geométrica, la ley de la reflexión de la luz nos dice que el ángulo del rayo incidente es igual al ángulo del rayo reflejado medido desde la normal. Comparando con las opciones, concluimos que la correcta es la c).
En la reflexión de la luz, el ángulo de incidencia es igual que el ángulo de reflexión de la luz.
Reactivo 48
¿Cuál es el índice de refracción de un material \mathrm{X} , si la velocidad de la luz a través de él es de 225,000 km/s? Considere la velocidad de la luz en el vacío como c=\mathrm{300,000} \mathrm{k}\mathrm{m}/\mathrm{s} .
- 1.25
- 1.333
- 2
- 0.1333
Solución:
La ley de la difracción de Snell nos dice que: el índice de refracción n de un material se calcula como el cociente de la velocidad de la luz en el vacío sobre la velocidad de la luz a través de él.
n=\frac{c}{v}
Sustituimos c y v dados por el enunciado.
n=\frac{\mathrm{300,000}}{\mathrm{225,000}}=1.333
En este caso no es necesario hacer conversión de unidades.
Comparando con las opciones, la correcta es la b).
Reactivo 49
Una onda electromagnética tiene una frecuencia de 1000 \mathrm{k}\mathrm{H}\mathrm{z} , si se propaga a la velocidad de la luz c=3\cdot {10}^{8} \mathrm{m}/\mathrm{s} , calcule su longitud de onda.
- 300 metros
- 30 metros
- 3 metros
- 3 micrómetros
Solución:
Para calcular la longitud de onda, empleamos la siguiente ecuación:
v=\lambda \cdot f
Despejamos la longitud de onda:
\lambda =\frac{v}{f}
Sustituimos.
\lambda =\frac{3\cdot {10}^{8} \mathrm{m}/\mathrm{s}}{1000000 \mathrm{H}\mathrm{z}}=300 \mathrm{m}
La longitud de onda es de 300 metros.
Concluimos que la respuesta correcta es la a).
Reactivo 50
La frecuencia de las ondas de radio es _______ que la frecuencia de las ondas infrarrojas.
- Mayor
- Igual
- Menor
- Cercana
Solución:
De los temas afines a las ondas electromagnéticas, sabemos que su principal clasificación es a través de la frecuencia, agrupándolas en categorías o bandas según determinados rangos bien definidos.
En base a dicha clasificación, las ondas de radio se encuentran por debajo de los 100 GHz, mientras que la radiación infrarroja se encuentra por encima de los 1 THz (1000000 GHz). En conclusión, la frecuencia de las ondas de radio es menor que la frecuencia de la radiación infrarroja. Completando la frase:
La frecuencia de las ondas de radio es menor que la frecuencia de las ondas infrarrojas.
La respuesta correcta es el inciso c).