En este tutorial vamos a resolver la ultima parte de la guía de ingreso a la UANL para el área de matemáticas. Desarrollaremos paso a paso cada ejercicio del 21 al 27, te invito a intentarlo y luego regresa a comprobar tus resultados.

La prueba de admisión a la Universidad Autónoma de Nuevo León consta de 2 partes, cada una con un temario distinto. Matemáticas es una de las asignaturas que debes estudiar para aprobar el examen de ingreso, mira la guía UANL 2021 y conoce el resto.
Guía UANL resuelta Parte III
En la siguiente tabla, tienes una división de los temas que compone cada una de las partes del examen:
| Partes del examen | Áreas | Reactivos | Tiempo |
|---|---|---|---|
| Primera | Pensamiento matemático y analítico | 50 | 90 |
| Estructura de la lengua y comprensión lectora | 50 | 90 | |
| Segunda | Inglés | 20 | 20 |
| Comprensión lectora | 20 | 30 | |
| Área de conocimiento 1 | 20 | 20 | |
| Área de conocimiento 2 | 20 | 20 | |
| Totales | 180 | 270 |
Reactivo 21: Derivada de una función
Determina la derivada de la función:
f\left(x\right)=5{x}^{4}+6{x}^{3}+7{x}^{2}+8x+1
- {f}^{\text{'}}\left(x\right)=20{x}^{3}-18{x}^{2}+14x+8
- {f}^{\text{'}}\left(x\right)=20{x}^{3}+18{x}^{2}+14x+8
- {f}^{\text{'}}\left(x\right)=20{x}^{3}+18{x}^{2}-14x+8
- {f}^{\text{'}}\left(x\right)=20{x}^{3}+18{x}^{2}+14x-8
Solución:
Para resolver cualquier derivada, debemos tener presente las fórmulas comunes, conocer las propiedades y saber aplicar la regla de la cadena. En el caso de un polinomio, solo debemos derivar cada uno de sus términos, aplicando la fórmula de la derivada de una potencia y la propiedad de constante por función.
Derivada de f\left(x\right) .
{f}^{\text{'}}\left(x\right)={\left(5{x}^{4}+6{x}^{3}+7{x}^{2}+8x+1\right)}^{\text{'}}
{f}^{\text{'}}\left(x\right)={\left(5{x}^{4}\right)}^{\text{'}}+{\left(6{x}^{3}\right)}^{\text{'}}+{\left(7{x}^{2}\right)}^{\text{'}}+{\left(8x\right)}^{\text{'}}+{\left(1\right)}^{\text{'}}
Aplicamos las fórmulas para la derivada de: una potencia y de una constante, respectivamente.
{f}^{\text{'}}\left(x\right)=4\bullet 5{x}^{4-1}+3\bullet 6{x}^{3-1}+2\bullet 7{x}^{2-1}+8\left(1\right)+0
{f}^{\text{'}}\left(x\right)=20{x}^{3}+18{x}^{2}+14x+8
La derivada de f\left(x\right) es 20{x}^{3}+18{x}^{2}+14x+8 .
Comparando con las opciones, la respuesta correcta se encuentra en el inciso b).
Reactivo 22: Problema de optimización
Tienes que delimitar el perímetro de un rectángulo de lados x у y con estambre y con un pedazo adicional debes agregar un pedazo paralelo a la cara x y al centro de la cara y . Para realizar este trabajo, solo dispones de 100 cm de estambre. ¿Cuáles son las dimensiones que encierran el área máxima?
- x=16.67 у y=25
- x=15.67 y y=22
- x=18.67 у y=23
- x=14.67 y y=27
Solución:
Realicemos un bosquejo rápido de la situación planteada por el enunciado:
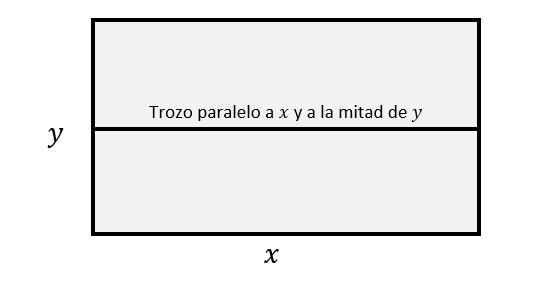
Vemos que las dimensiones del rectángulo son x y y , por tanto, el área del mismo mide A=xy . Por otro lado, el perímetro es la suma de los lados más, el trozo paralelo a x , es decir, el perímetro mide P=3x+2y , incluyendo al trozo.
El enunciado nos dice que la cantidad de estambre disponible es 100 cm, por lo que igualamos el perímetro a 100.
100=3x+2y
De esta expresión, podemos despejar a x o y y sustituirla en la ecuación del área, ya que, es el área la función que debemos optimizar.
Despejando a x .
x=\frac{100-2y}{3}
Sustituyendo.
A=\left(\frac{100-2y}{3}\right)y=\frac{100y-2{y}^{2}}{3}
Ahora solo nos queda derivar al área respecto de y , igualar a cero y calcular el valor óptimo.
\frac{dA}{dy}=\frac{100-4y}{3}
Igualamos a cero y despejamos y .
{A}_{max}\to \frac{dA}{dy}=0
\therefore \frac{100-4y}{3}=0
y=25
Finalmente, sustituimos en \frac{100-2y}{3} para calcular a x
x=\frac{100-2\left(25\right)}{3}=16.\underset{\_}{6}\approx 16.67
Las dimensiones del rectángulo para lograr el área máxima son:
x=16.67 у y=25
La respuesta correcta es la opción a).
Reactivo 23: Límite de una función
Calcula el límite de la siguiente función:
\underset{x\to 1}{lim} \frac{10{x}^{3}-26{x}^{2}+22x-6}{(x-1{)}^{2}}
- 8
- 4
- 3
- 2
Solución:
Comenzamos por evaluar a la función en el límite para comprobar si presenta o no una indeterminación en dicho valor.
\underset{x\to 1}{lim} \frac{10{x}^{3}-26{x}^{2}+22x-6}{(x-1{)}^{2}}=\frac{10{\left(1\right)}^{3}-26{\left(1\right)}^{2}+22\left(1\right)-6}{(1-1{)}^{2}}=\frac{0}{0}
Existe una indeterminación \frac{0}{0} . Debemos aplicar artificios matemáticos para resolverla. Extraemos factor común 2.
\underset{x\to 1}{lim} \frac{10{x}^{3}-26{x}^{2}+22x-6}{(x-1{)}^{2}}=2\underset{x\to 1}{lim} \frac{5{x}^{3}-13{x}^{2}+11x-3}{(x-1{)}^{2}}
Debido a que el denominador ya se encuentra fractorizado, debemos intentar factorizar el polinomio de tercer grado del numerador. Si no cuentas con calculadora científica, es casi imposible calcular las raíces de un polinomio cúbico a mano, por ello, aplicaremos un pequeño truco.
Debido a que x=1 hace que el polinomio cúbico se haga cero, dicho valor es una de sus raíces. Por lo tanto, podemos aplicar la siguiente factorización:
5{x}^{3}-13{x}^{2}+11x-3=\left(x-1\right)\left(a{x}^{2}+bx+c\right)
Para conocer el valor de a , b y c desarrollamos el producto e igualamos los términos con la misma potencia.
5{x}^{3}-13{x}^{2}+11x-3=a{x}^{3}+\left(b-a\right){x}^{2}+\left(c-b\right)x-c
Igualamos términos.
a=5
b-a=-13\to b=-8
c-b=11\to c=3
-c=-3\to c=3
La factorización queda:
5{x}^{3}-13{x}^{2}+11x-3=\left(x-1\right)\left(5{x}^{2}-8x+3\right)
Sustituimos en el límite:
2\underset{x\to 1}{lim} \frac{\left(x-1\right)\left(5{x}^{2}-8x+3\right)}{(x-1{)}^{2}}=2\underset{x\to 1}{lim} \frac{5{x}^{2}-8x+3}{x-1}
Evaluamos para comprobar.
2\underset{x\to 1}{lim} \frac{5{x}^{2}-8x+3}{x-1}=2\bullet \frac{5{\left(1\right)}^{2}-8\left(1\right)+3}{1-1}=\frac{0}{0}
Aún existe una indeterminación, debemos factorizar de nuevo. Esta vez podemos utilizar la fórmula de segundo grado.
2\underset{x\to 1}{lim} \frac{5{x}^{2}-8x+3}{x-1}=2\underset{x\to 1}{lim} \frac{\left(x-1\right)\left(5x-3\right)}{x-1}=2\underset{x\to 1}{lim}\left(5x-3\right)
Evaluamos.
2\underset{x\to 1}{lim}\left(5x-3\right)=2\bullet \left(5\left(1\right)-3\right)=4
Comparando con las opciones, concluimos escogiendo como correcta la opción b).
Reactivo 24: Integral definida
Un resorte de 20 cm se estira 4 cm aplicando una fuerza de 12 N. Calcula el trabajo necesario para que el resorte se estire 10 cm.
- 2 J
- 0.75 J
- 3 J
- 1.5 J
Solución:
De los temas referentes a mecánica clásica, sabemos que la fuerza desarrollada por un resorte se modela mediante le Ley de Hooke:
{F}_{r}=-kx
Donde k es la constante elástica del resorte y x es el desplazamiento sufrido por el resorte. Los primeros datos que proporciona el problema son para obtener la constante k .
{F}_{r}=12 N
x=0.04 m
k=\frac{{F}_{r}}{x}=\frac{12 N}{0.04 m}=300 N/m
Sustituimos en la Ley de Hooke:
{F}_{r}=-300x
El trabajo se calcula como la integral de la fuerza sobre el recorrido, como el desplazamiento es lineal, la integral queda:
{W}_{\mathrm{1,2}}={\int }_{0}^{\Delta x}300x dx
Sacamos la constante de la integral y aplicamos la fórmula de la integral de una potencia.
{W}_{\mathrm{1,2}}=50{\int }_{0}^{\Delta x}x dx=\frac{50}{2}\Delta {x}^{2}
El desplazamiento en metros es:
\Delta x=0.1 m
{W}_{\mathrm{1,2}}=\frac{300}{2}{\left(0.1\right)}^{2}=1.5 J
Son necesarios 1.5 Joules de trabajo para estirar el resorte 10 cm.
Comparando con las opciones, escogemos como correcta la d).
Reactivo 25: Binomio cúbico
Desarrolla el siguiente binomio al cubo.
(x+3{)}^{3}- 27+27x+9{x}^{2}+{x}^{3}
- {x}^{3}+9{x}^{2}+27x-27
- {x}^{3}+9{x}^{2}-27x-27
- {x}^{3}-9{x}^{2}+27x-27
Solución:
Para encontrar el desarrollo del binomio al cubo, debemos descomponer a la potencia como el producto de su base y luego multiplicar de dos en dos.
(x+3{)}^{3}=\left(x+3\right)\left(x+3\right)\left(x+3\right)
Realizamos el producto entre las primeras dos.
(x+3{)}^{3}=\left({x}^{2}+3x+3x+9\right)\left(x+3\right)=\left({x}^{2}+6x+9\right)\left(x+3\right)
Ahora el trinomio con el binomio restante.
=\left({x}^{2}+6x+9\right)\left(x+3\right)={x}^{3}+6{x}^{2}+9x+3{x}^{2}+18x+27
Agrupando nos queda:
(x+3{)}^{3}={x}^{3}+9{x}^{2}+27x+27
Comparando con las opciones, indicamos como correcta la a).
Reactivo 26: Operaciones entre conjuntos
Sean A el conjunto de los números pares del intervalo \left[\mathrm{0,12}\right) y B el conjunto de los números primos en el intervalo \left(\mathrm{1,65}\right) . Determina A\cup B .
- A\cup B=\{\mathrm{2,3},\mathrm{4,5},\mathrm{6,7},\mathrm{8,10,11,13,19,23,29,31,37,41,43,47,53,59,61}\}
- A\cup B=\{\mathrm{2,3},\mathrm{4,5},\mathrm{6,7},\mathrm{8,10,11,13,17,19,23,29,31,41,43,47,53,59,61}\}
- A\cup B=\{\mathrm{2,3},4,\mathrm{5,6},\mathrm{7,8},\mathrm{10,11,12,13,17,19,23,29,31,37,41,43,47,53,59,61}\}
- A\cup B=\{\mathrm{2,3},\mathrm{4,5},\mathrm{6,7},\mathrm{8,10,11,13,17,19,23,29,31,37,41,43,47,53,59,61}\}
Solución:
Antes de realizar la unión de ambos conjuntos, debemos identificar cuáles son los elementos de cada uno. El conjunto A está formado por los enteros en el intervalo \left[\mathrm{0,12}\right) , con el 12 excluido, es decir, no podemos considerarlo.
A=\left\{2, 4, 6, 8, 10\right\}
Por otra parte, el conjunto abierto en sus extremos B , consta de los primos entre 1 y 65, el 1 no va incluido porque es el extremo inferior.
B=\left\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61\right\}
La unión de A y B , es otro conjunto que contiene los elementos de A y B a la vez; por tanto:
A\cup B=\{\mathrm{2,3},\mathrm{4,5},\mathrm{6,7},\mathrm{8,10,11,13,17,19,23,29,31,37,41,43,47,53,59,61}\}
Comparando con las opciones, la respuesta correcta es la d).
Reactivo 27: Teorema de Pitágoras
Se requiere colocar un tirante de apoyo en la parte superior del poste de la luz de 12 m, el extremo opuesto del tirante se desea colocar a 15 m de la base del poste. ¿Cuál es el largo del tirante que se debe comprar?
- 21.25m
- 20.35m
- 19.21m
- 18.53m
Solución:
Para visualizar mejor lo que plantea el problema, haremos un dibujo rápido de la situación.
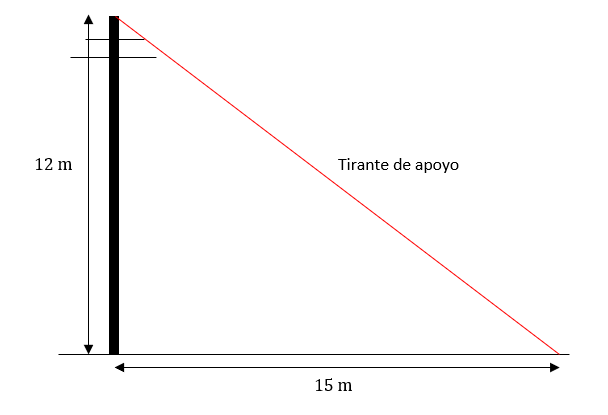
La longitud del tirante se calcula aplicando el teorema de Pitágoras.
Tirante=\sqrt{{12}^{2}+{15}^{2}}
Evaluamos.
Tirante=\sqrt{144+225}
Tirante=\sqrt{369}=19.21 m
Se deben comprar al menos unos 19.21 metros de tirante.
La respuesta correcta es el inciso c).

