¡Hola de nuevo aspirante! En esta entrada estaremos resolviendo el segundo grupo de reactivos para el área de matemáticas del examen de admisión a la UANL. Si no has visto la primera parte de la guía resuelta UANL puedes visitarla haciendo click en el botón de abajo.

Te recomiendo desarrollar los reactivos por tu cuenta antes de seguir y luego regresa para aclarar dudas. Recuerda que además de las áreas específicas de tu carrera, debes dominar los conocimientos generales para asegurar el ingreso.
Guía UANL resuelta Parte II
La prueba de admisión de la Universidad Autónoma de Nuevo León esta dividida en dos partes: conocimientos generales y por área. Los temas, duración y cantidad de reactivos para cada una se muestran en la siguiente tabla:
| Partes del examen | Áreas | Reactivos | Tiempo |
|---|---|---|---|
| Primera | Pensamiento matemático y analítico | 50 | 90 |
| Estructura de la lengua y comprensión lectora | 50 | 90 | |
| Segunda | Inglés | 20 | 20 |
| Comprensión lectora | 20 | 30 | |
| Área de conocimiento 1 | 20 | 20 | |
| Área de conocimiento 2 | 20 | 20 | |
| Totales | 180 | 270 |
Reactivo 11: Trigonometría
Resuelve el siguiente triángulo.
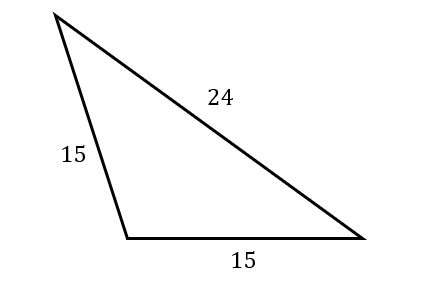
- {37}^{\circ },{38}^{\circ },{105}^{\circ }
- {35}^{\circ },{36}^{\circ },{109}^{\circ }
- {36.87}^{\circ },{36.87}^{\circ },{106.26}^{\circ }
- {37.87}^{\circ },{37.87}^{\circ },{104.26}^{\circ }
Solución:
Cuando un problema de trigonometría solicita resolver un triángulo, debemos encontrar el valor de sus tres lados y ángulos. En este caso, ya conocemos los tres lados y solo hacen falta los ángulos.
El triángulo en cuestión es isósceles y obtusángulo. Es decir, posee dos ángulos iguales y el tercero es mayor a 90°. Tenemos diferentes dos posibilidades para resolver el problema:
- Aplicando la ley del coseno
- Trazando una perpendicular desde el punto medio del segmento que mide 24 unidades hasta el vértice opuesto para formar dos triángulos rectángulos. Luego, aplicamos identidades trigonométricas para hallar el ángulo agudo y con el calcular el obtuso
Esta vez, emplearemos el segundo camino. Trazando la perpendicular, el triángulo quedaría de la siguiente manera:
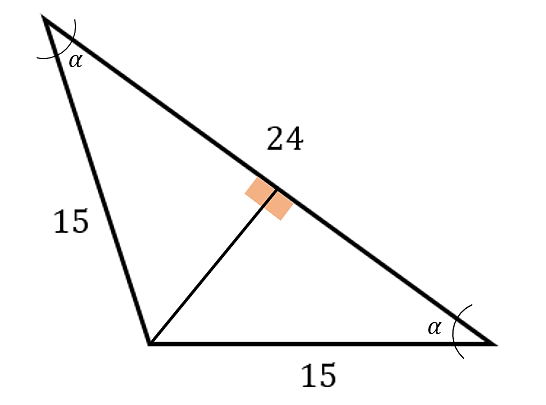
De esta forma, \alpha se calcularía como:
cos\alpha =\frac{12}{15}
Aplicamos identidad inversa.
\alpha ={\mathrm{cos}}^{-1}\left(\frac{12}{15}\right) =36.87°
Por último, aplicamos la propiedad de la suma de ángulos internos en un triángulo:
\alpha +\alpha +\beta =180°
\beta =180°-2\alpha
\beta =180°-2\left(36.87°\right)
\therefore \beta =106.26°
Los ángulos internos al triángulo son:
{37.87}^{\circ },{37.87}^{\circ },{104.26}^{\circ }
Comparando con las opciones, la respuesta correcta está en la c).
Reactivo 12: Problemas geométricos
En tu clase de matemáticas tu profesor corta un pedazo de hoja rectangular por una de sus diagonales y te dice que la diagonal mide 34 centímetros y el perímetro de cada triángulo es de 80 centímetros. ¿Cuáles eran las dimensiones originales de la hoja?
- Largo 15cm y ancho 31cm
- Largo 16 cm y ancho 30cm
- Largo 16 cm y ancho 31cm
- Largo 15cm y ancho 30cm
Solución:
Debido a que las hojas de papel son rectangulares, sus lados paralelos miden igual. En este caso llamaremos x a los lados paralelos horizontales, y a los lados paralelos verticales y a la diagonal la llamaremos z .
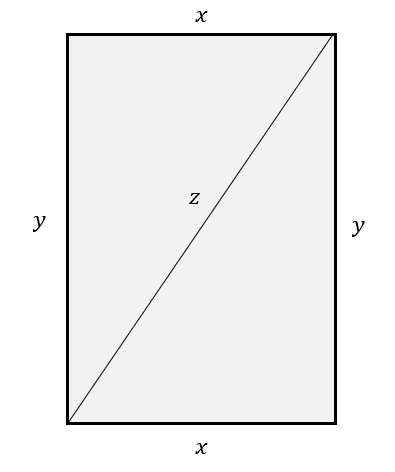
El perímetro del triángulo se calcula como:
x+y+z=80
Además, por el teorema de Pitágoras, la diagonal z es igual a:
{z}^{2}={34}^{2}={x}^{2}+{y}^{2}
Sustituyendo y reordenando nos queda:
x+y=80-34\to x+y=46
{34}^{2}={x}^{2}+{y}^{2}\to {x}^{2}+{y}^{2}=1156
Obtenemos un sistema de 2 ecuaciones con 2 incógnitas.
\left\{\begin{array}{c}x+y=46 \\ {x}^{2}+{y}^{2}=1156\end{array}\right.
Geométricamente hablando, este SE corresponde a la intersección entre una circunferencia y una recta. Despejamos de la primera ecuación a x y la expresión resultante la sustituimos en la segunda ecuación.
x+y=46\to x=46-y
Sustituyendo.
{\left(46-y\right)}^{2}+{y}^{2}=1156
Desarrollamos el producto notable.
{46}^{2}-92y+{y}^{2}+{y}^{2}=1156
2{y}^{2}-92y+2116=1156
2{y}^{2}-92y+2116-1156=0
2{y}^{2}-92y+960=0
{y}^{2}-46y+480=0
Aplicamos la fórmula de la resolvente para calcular los posibles valores de y .
{y}_{\mathrm{1,2}}=\frac{-\left(-46\right)\pm \sqrt{{\left(-46\right)}^{2}-4\left(1\right)\left(480\right)}}{2\left(1\right)}
{y}_{1}=30;{y}_{2}=16
Ahora, debemos sustituir ambas soluciones en una de las ecuaciones para obtener los posibles valores de x . Por supuesto, lo haremos en la primera ecuación porque es más sencilla de despejar.
Sustituyendo {y}_{1} .
{x}_{1}=46-30=16
Sustituyendo {y}_{2} .
{x}_{2}=46-16=30
Las soluciones son:
{x}_{1}=16 cm; {y}_{1}=30 cm
{x}_{2}=30 cm; {y}_{2}=16 cm
Básicamente la misma hoja, pero rotada 90°.
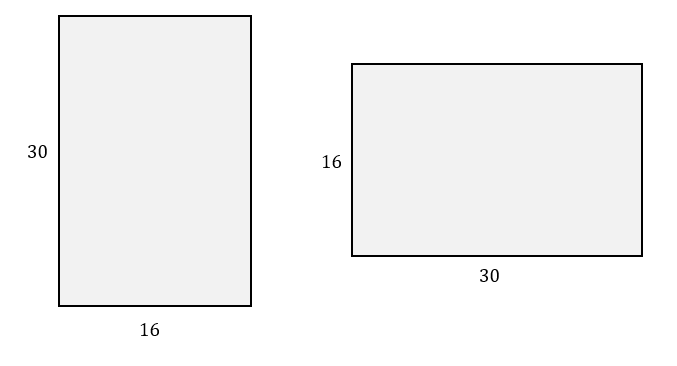
Examinando las opciones, la única que cuenta con esta combinación es la b).
Largo 16 cm y ancho 30cm
Concluimos entonces que la respuesta correcta está en el inciso b).
Reactivo 13: Ecuación de la elipse
Determina la ecuación de la elipse si sabemos que pasa por el punto \left(\mathrm{0,4}\right) , está centrada en el origen y tiene excentricidad \frac{3}{5} .
- \frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1
- \frac{{x}^{2}}{23}+\frac{{y}^{2}}{26}=1
- \frac{{x}^{2}}{25}+\frac{{y}^{2}}{26}=1
- \frac{{x}^{2}}{25}+\frac{{y}^{2}}{26}=1
Solución:
El problema solicita que calculemos la ecuación ordinaria de la elipse, cuyo centro es \left(\mathrm{0,0}\right) , pasa por \left(\mathrm{0,4}\right) y tiene excentricidad e=\frac{3}{5} . Sustituyendo el centro, la expresión quedaría como:
\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1
Por otra parte, la excentricidad de una elipse es igual al cociente entre c y a ; donde c es la distancia entre el centro y uno de los focos sobre el eje focal.
e=\frac{c}{a}
Si e=\frac{3}{5} entonces:
\frac{3}{5}=\frac{c}{a}
c=\frac{3}{5}a
Además, a , b y c en la elipse obedecen la siguiente relación:
c=\sqrt{{a}^{2}-{b}^{2}}
Sustituyendo nos queda:
\frac{3}{5}a=\sqrt{{a}^{2}-{b}^{2}}
\frac{9}{25}{a}^{2}={a}^{2}-{b}^{2}
\frac{16}{25}{a}^{2}-{b}^{2}=0
Tenemos esta primera ecuación, ahora vamos a sustituir \left(\mathrm{0,4}\right) en la ecuación de la elipse.
\frac{0}{{a}^{2}}+\frac{{4}^{2}}{{b}^{2}}=1
Despejando a b .
{b}^{2}={4}^{2}
b=4
Sustituimos a b en la primera ecuación.
\frac{16}{25}{a}^{2}-16=0
Despejando a .
{a}^{2}=25
a=5
Con esto tenemos todos los parámetros de la ecuación de la elipse.
\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1
Es una elipse con eje focal sobre el eje x .
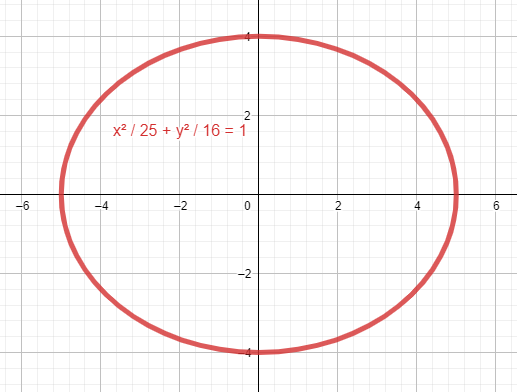
La respuesta correcta es la opción a).
Reactivo 14: Ecuación de la elipse
Uno de los túneles de una autopista es la mitad de una elipse, si sabemos que el punto más alto del túnel mide 20 pies y el ancho del túnel es de 24 pies. Determina la ecuación de la elipse centrada en el origen.
- \frac{{x}^{2}}{10}+\frac{{y}^{2}}{576}=1
- \frac{{x}^{2}}{144}+\frac{{y}^{2}}{100}=1
- \frac{{y}^{2}}{100}+\frac{{x}^{2}}{576}=1
- \frac{{x}^{2}}{144}+\frac{{y}^{2}}{400}=1
Solución:
Para visualizar mejor este problema, hagamos un pequeño esbozo de la situación planteada por el enunciado.
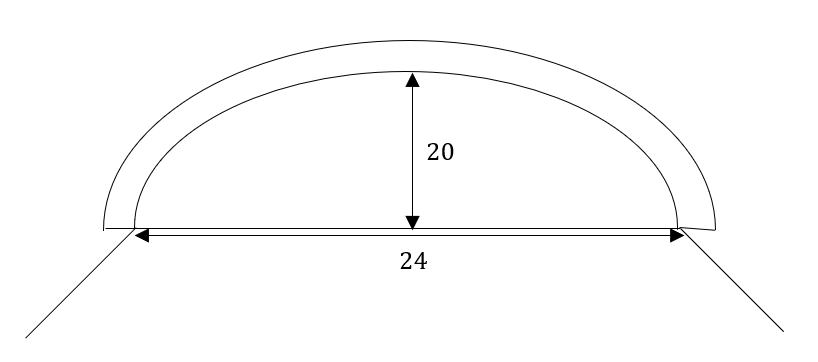
En base a la información que nos ofrece el enunciado, sabemos que el centro de la elipse es \left(\mathrm{0,0}\right) , además, a partir de la imagen sabemos que b=20 .
\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{20}^{2}}=1
La elipse pasa por el punto \left(\mathrm{12,0}\right) , por tanto, podemos sustituirlo en la ecuación y calcular el valor de a .
\frac{{12}^{2}}{{a}^{2}}+\frac{{0}^{2}}{{20}^{2}}=1\to {a}^{2}={12}^{2}
Sustituyendo nos queda:
\frac{{x}^{2}}{{12}^{2}}+\frac{{y}^{2}}{{20}^{2}}=1
\frac{{x}^{2}}{144}+\frac{{y}^{2}}{400}=1
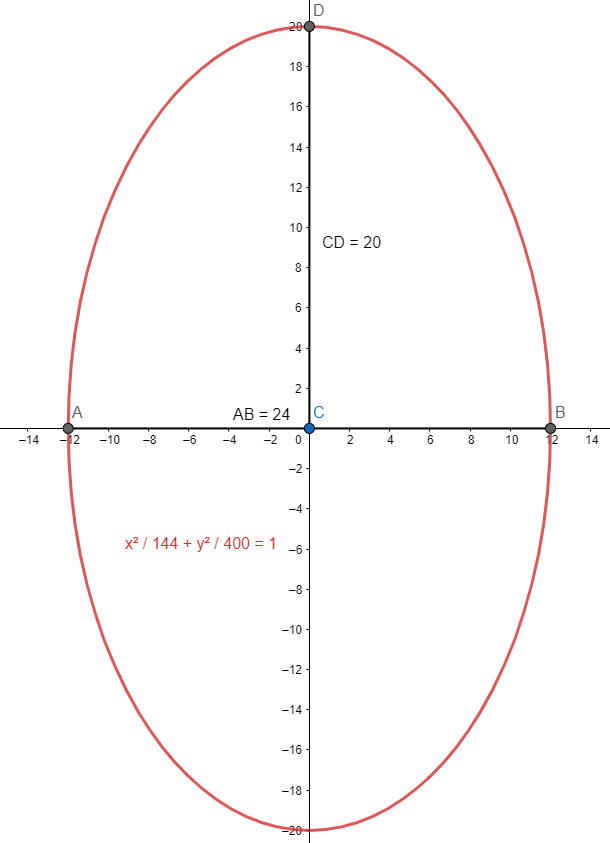
La respuesta correcta se encuentra en el inciso d).
Reactivo 15: Ecuación de la recta
Determina la ecuación de la recta que pasa por los puntos \left(\mathrm{1,2}\right) y \left(\mathrm{5,7}\right) .
- 5x+4y=3
- 5x+4y=-3
- 5x-4y=-3
- 5x-4y=3
Solución:
En este caso, debemos utilizar la forma punto-pendiente de la recta para calcular su ecuación. Comenzamos por determinar la pendiente:
m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}
Donde:
\left({x}_{1},{y}_{1}\right)=\left(\mathrm{1,2}\right)
\left({x}_{2},{y}_{2}\right)=\left(\mathrm{5,7}\right)
Sustituimos.
m=\frac{7-2}{5-1}=\frac{5}{4}
Ahora, sustituimos el punto \left({x}_{1},{y}_{1}\right) y la pendiente en la forma punto pendiente de la recta.
y-{y}_{1}=m\left(x-{x}_{1}\right)
Sustituimos y desarrollamos.
y-2=\frac{5}{4}\left(x-1\right)
y-2=\frac{5}{4}x-\frac{5}{4}
4y-8=5x-5
5x-4y=5-8
5x-4y=-3
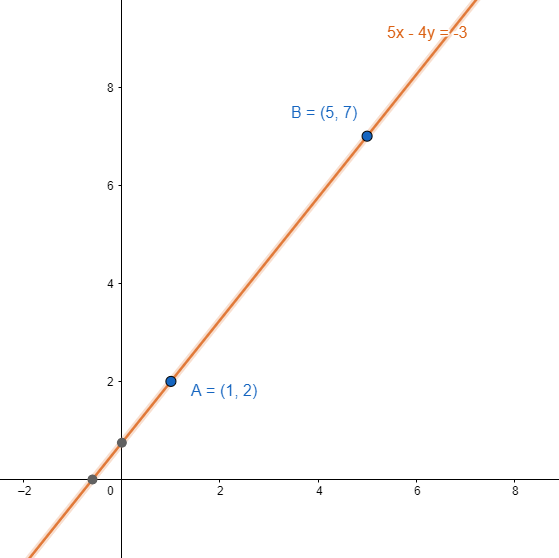
Concluimos escogiendo como respuesta correcta la opción c).
Reactivo 16: Función afín
Se sabe que al ingresar a una empresa el salario base es de \$37855 y al haber transcurrido cinco años el salario asciende a \$47123 . Determina una función lineal que permite determinar el salario en función del tiempo.
- F\left(t\right)=1853.6t+37855
- F\left(t\right)=-1853.6t+37855
- F\left(t\right)=1853.6t-37855
- F\left(t\right)=-1853.6t-37855
Solución:
En este caso, la variable independiente es el tiempo, que se indica en años. Por otro lado, la variable dependiente de nuestra función lineal es el salario que depende del tiempo. Los puntos por los que debe pasar la función lineal son:
{P}_{1}\left({t}_{1},F\left({t}_{1}\right)\right)={P}_{1}\left(\mathrm{0,37855}\right)
{P}_{2}\left({t}_{2},F\left({t}_{2}\right)\right)={P}_{2}\left(\mathrm{5,47123}\right)
Empleamos la forma explícita de la recta, porque conocemos el corte con el eje de las ordenadas b=37855 , solo nos queda calcular la pendiente.
F\left(t\right)=mt+b
Sustituyendo b .
F\left(t\right)=mt+37855
La pendiente se calcula con la siguiente ecuación.
m=\frac{F\left({t}_{2}\right)-F\left({t}_{1}\right)}{{t}_{2}-{t}_{1}}=\frac{47123-37855}{5-0}=1853.6
Finalmente:
F\left(t\right)=1853.6t+37855
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 17: Ecuación de la recta
Una recta pasa por los puntos \left(\mathrm{5,8}\right) y (1,y) . Si la pendiente de la recta es m=\frac{7}{4} . ¿Cuál es el valor de y ?
- y=-1
- y=-2
- y=1
- y=2
Solución:
Este problema se resuelve empleando la ecuación de pendiente de una recta, sustituyendo en ella los valores dados y despejando a y .
m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}
En este caso y={y}_{1} . Sustituimos y despejamos.
\frac{7}{4}=\frac{8-y}{5-1}
\frac{7}{4}=\frac{8-y}{4}
8-y=7\to y=1
Finalmente: el valor de y para que la pendiente sea \frac{7}{4} es 1.
La respuesta correcta está en el inciso c).
Reactivo 18: Rectas perpendiculares
Determina la ecuación de la familia de las rectas perpendiculares a la recta y=8x+1 .
- y=\frac{1}{3}x+b
- y=\frac{1}{8}x+5
- y=-\frac{1}{8}x+b
- y=-\frac{1}{3}x+5
Solución:
Dos o más rectas son perpendiculares entre sí, cuando el ángulo formado entre ellas es igual a 90°.
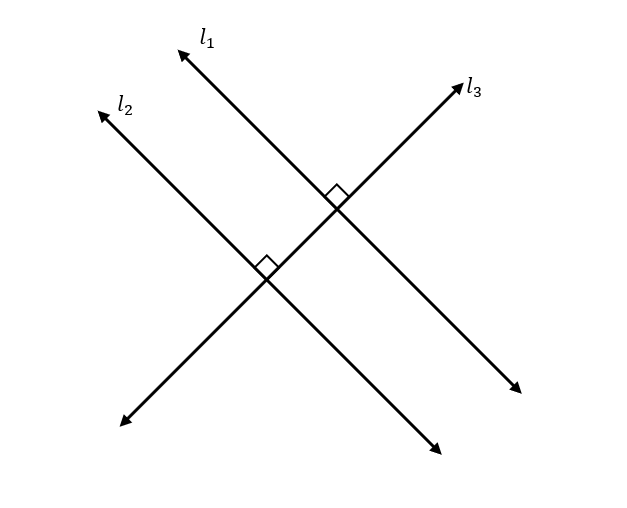
En la imagen, {l}_{1} y {l}_{2} son perpendiculares a {l}_{3} y paralelas entre ellas, es decir, pertenecen a la misma familia de rectas que son perpendiculares a {l}_{3} . Lo único que las diferencia, es el corte con el eje de las ordenadas b .
Por lo tanto, la ecuación que describe a la familia de rectas perpendiculares a otra recta dada {l}_{d} es:
y={m}_{\perp d}x+b
Donde:
{m}_{\perp d}=-\frac{1}{{m}_{d}}
Si la recta dada en este caso es {l}_{d}:y=8x+1 y su pendiente {m}_{d}=8 , la pendiente de las rectas perpendiculares a ella es:
{m}_{\perp d}=-\frac{1}{8}
Finalmente.
y=-\frac{1}{8}x+b
Comparando con las opciones, la respuesta correcta está en el inciso c).
Reactivo 19: Área de figuras planas
Determina el área del isodecágono de 15 cm de lado.
- 7102.97{cm}^{2}
- 14205.94{cm}^{2}
- 7102.97cm
- 14205.94cm
Solución:
Un isodecágono es un polígono de 10 lados que poseen la misma longitud, entre otras palabras, eso último es lo que indica el prefijo iso. El área de cualquier decágono regular se puede calcular a partir de la longitud de uno de sus lados empleando la siguiente ecuación:
A=\frac{20{l}^{2}}{4tan\left(\frac{\pi }{20}\right)}
Donde l es la longitud del lado. Solo nos queda sustituir y resolver las operaciones correspondientes.
A=\frac{20{\left(15 cm\right)}^{2}}{4tan\left(\frac{\pi }{20}\right)}=7102.97 {cm}^{2}
Concluimos seleccionando como respuesta correcta la opción a).
Reactivo 20: Triángulos semejantes
Jorge quiere determinar la altura de un edificio que a cierta hora proyecta una sombra de 80 metros, si a esa misma hora la sombra de Jorge es de 10 metros, ¿Cuál es la altura del edificio, si se sabe que Jorge mide 2 metros?
- 17 m
- 16 m
- 15 m
- 14 m
Solución:
Hagamos un bosquejo rápido de la situación planteada en el problema para analizarla mejor.
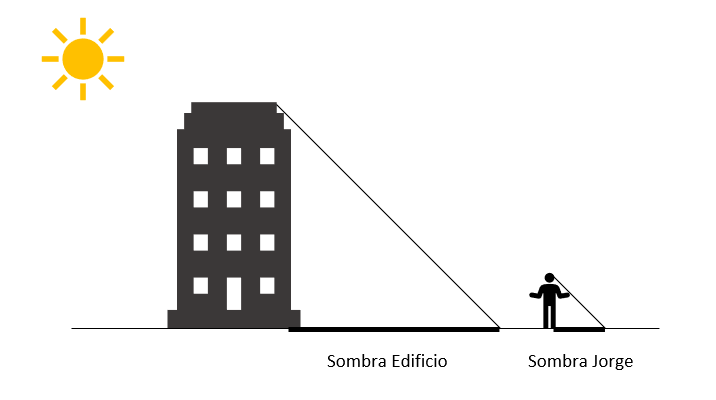
Como se puede observar, se forman dos triángulos: uno que relaciona la altura del edificio con su sombra y el otro la altura de Jorge con la sombra. Debido a que el sol está proyectando ambas sombras a la misma hora del día, el ángulo de inclinación hipotenusa-sombra es igual para ambos triángulos. Decimos que son triángulos semejantes.
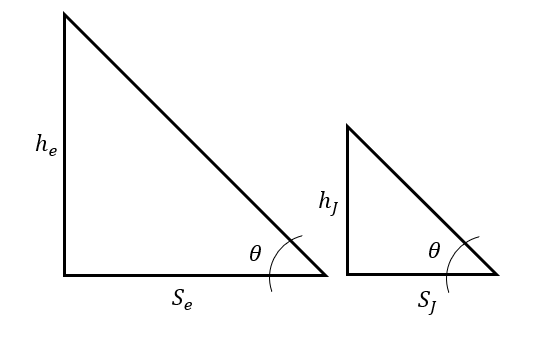
Aplicamos el criterio de semejanza de lados:
\frac{{h}_{e}}{{S}_{e}}=\frac{{h}_{J}}{{S}_{J}}
Despejamos la altura del edificio.
{h}_{e}=\frac{{h}_{J}}{{S}_{J}}{S}_{e}
Sustituimos los valores.
{h}_{e}=\frac{2 m}{10 m}80 m=16 m
El edificio tiene 16 metros de altura.
La respuesta correcta se encuentra en el inciso b).


