¡Bienvenido aspirante! A lo largo del post estaremos resolviendo la primera parte de la guía UANL 2021 de matemáticas para el examen de ingreso. Ten en cuenta que el área dependerá de la facultad a la que desees ingresar.

A continuación, te dejo un resumen del proceso de admisión:
- Períodos de ingreso: Dos al año.
- Inicio de registro: Abril y Octubre
- Carreras ofertadas: 100+
- Examen de admisión: Pearson
- Porcentaje de Aceptación: 50%
Estructura del examen de la UANL
La prueba de ingreso a la Universidad Autónoma de Nuevo León se divide en dos partes, la primera corresponde a conocimientos generales y la segunda a los conocimientos por área.
La siguiente es una tabla resumen con el área, número de reactivos y el tiempo que tendrás para resolverlos.
| Partes del examen | Áreas | Reactivos | Tiempo |
|---|---|---|---|
| Primera | Pensamiento matemático y analítico | 50 | 90 |
| Estructura de la lengua y comprensión lectora | 50 | 90 | |
| Segunda | Inglés | 20 | 20 |
| Comprensión lectora | 20 | 30 | |
| Área de conocimiento 1 | 20 | 20 | |
| Área de conocimiento 2 | 20 | 20 | |
| Totales | 180 | 270 |
Recuerda medir el tiempo que tardas con cada reactivo. Una gran parte de los aspirantes que reprueba, olvidó mejorar sus tiempos durante la preparación.
Temario del Área de Matemáticas
El área de matemáticas en la segunda parte del examen, se centra en las ramas de aritmética, geometría y cálculo, con especial énfasis en los siguientes temas:
Aritmética
- Operaciones de números naturales y enteros
- Operaciones de números reales y notación científica
- Álgebra
- Métodos para la representación de lugares geométricos; ecuaciones lineales y cuadráticas
- Operaciones básicas con fracciones algebraicas y radicales Leyes de los exponentes y radicales
Geometría
- Paralelismo, congruencia, semejanza y rectas
- Cálculo de perímetros y áreas de figuras planas
- Figuras geométricas: perímetro, área y volumen
- Pendiente de la recta y ángulo entre rectas
- Ecuaciones y gráficas de la circunferencia, la parábola, la elipse y la hipérbola
Cálculo
- Dominio, contradominio, tabulación y graficación
- Operaciones con funciones
- Limites de las funciones: polinomiales, racionales, trigonométricas, logarítmicas o exponenciales
- Derivada de funciones algebraicas y no algebraicas
- La integral definida
El temario de la guía de ingreso UANL diseñada por Pearson es extenso, recuerda estudiar el resto de las asignaturas.
Guía UANL resuelta Parte I
Un error común entre los aspirantes, es revisar la solución antes de intentarlo por cuenta propia. Si aún no resuelves ninguno ¡hazlo! y vuelve para salir de dudas o comprobar el resultado.
Antes de comenzar a estudiar, es necesario que identifiques tus puntos débiles para fortalecerlos y lograr la mejor puntuación en el examen. Recuerda que los reactivos de la prueba son aleatorios y puede salir cualquiera del temario, asegúrate de estudiarlos muy bien.
Reactivo 1: Depósito desconocido
Al inicio del año en tu cuenta bancaria tenías -\$458 , en enero recibiste un depósito por \$1500 , durante febrero tus gastos ascendieron a \$850 , en marzo uno de tus amigos te pago \$200 por un préstamo que le había realizado. En abril, por dos meses consecutivos, tuviste que pagar \$300 cada mes y te avisaron que recibiste un depósito, pero no te dieron el monto. Si finalmente en junio tu cuenta bancaria tenía \$1725 . ¿Cuál fue el monto del depósito desconocido?
- \$763
- \$1933
- \$1369
- \$568
Solución:
En este problema, debemos encontrar cuál fue la cantidad desconocida depositada a nuestra cuenta. Para ello, el enunciado nos indica cuales fueron los ingresos, egresos, monto inicial y monto final durante la primera mitad del año (de enero a junio).
Debemos igualar el monto final, es decir \$1725 , al monto inicial junto a los ingresos y egresos de cada mes. De esta forma, tendremos una ecuación cuya incógnita es el depósito desconocido DD , que podremos despejar aplicando las propiedades de la igualdad.
Comencemos por ordenar correctamente los montos en la ecuación. En el primer miembro irá el monto final y al segundo el inicial junto a los ingresos-egresos. El monto inicial es negativo, quiere decir que teníamos saldo deudor y, en enero, recibimos un ingreso por \$1500 .
1725=-458+1500
En febrero solo hubo un total de gastos igual a \$850 , se escribe negativo porque es un egreso.
1725=-458+1500-850
Durante el mes de marzo recibiste \$200 como pago a un préstamo.
1725=-458+1500-850+200
Durante abril y mayo tuviste que pagar \$300 . Escribimos 300 negativos dos veces.
1725=-458+1500-850+200-300-300
Luego, vino el depósito misterioso DD que va positivo porque fue un ingreso a tu cuenta.
1725=-458+1500-850+200-300-300+DD
Ahora, simplificamos las sumas y restas, para finalmente despejar DD .
1725=1042-850+200-300-300+DD
1725=192+200-300-300+DD
1725=392-600+DD
1725=-208+DD
Despejando nos queda:
1725+208=DD\to DD=1933
El depósito misterioso fue de \$1933 .
Concluimos el ejercicio escogiendo como correcta la opción b).
Reactivo 2: Dinero por devolución
Durante un año fiscal Roberto realiza cuatro pagos de impuestos provisionales sobre la renta de \$5896,\$2389,\$7589 y \$3258 . Al cierre del año fiscal, en su declaración anual, el impuesto total a cargo por todas sus actividades fue de \$18569 . ¿Cuánto dinero debería de recibir por concepto de devolución o cuánto tendría que pagar para terminar en cero su ejercicio fiscal?
- Recibirá \$563 por concepto de devolución
- Debe pagar \$563 para terminar en cero el ejercicio
- Su balance financiero está en ceros
- Debe pagar -\$563 para terminar en ceros el ejercicio
Solución:
Para saber si Roberto debe pagar o se le tiene que devolver dinero, tenemos que sumar todos los montos de los pagos por impuestos provisionales que realizó.
Si el resultado es mayor a \$18569 , entonces tiene que recibir una devolución igual a IP-\$18569 . En caso contrario, debe pagar una cantidad igual a \$18569-IP .
Sumamos los pagos realizados por Roberto.
IP=\$5896+\$2389+\$7589+\$3258=\$19132
Los IP pagados son mayores al cargo de sus actividades, por tanto, se le debe devolver la siguiente cantidad:
Devolución=\$19132-\$18569=\$563
Concluimos el reactivo indicando como respuesta correcta la opción a) Recibirá \$563 por concepto de devolución.
Reactivo 3: Valor absoluto
Simplifica la siguiente expresión:
|-3|+4+|4-6|+\left\{5\right(3-5)+2\}-25
- 24
- 56
- -56
- -24
Solución:
Para resolver expresiones aritméticas en la que están presentes numerosas operaciones, debemos seguir las reglas de jerarquía para dichas operaciones:
- Llaves
- Corchetes
- Paréntesis
- Potencias y radicales
- Multiplicaciones y divisiones
- Sumas y restas
Las operaciones más pesadas inician desde resolver el interior de llaves, hasta terminar con sumas y restas. En este caso, tenemos presente el operador valor absoluto en la expresión. Nos indica que sea cual sea el resultado en su interior, siempre saldrá positivo.
\left|5\right|=5;\left|-27\right|=27
Aclarados estos puntos, procedemos a la solución de la expresión. Iniciamos por el interior de las llaves.
|-3|+4+|4-6|+\left\{5\right(3-5)+2\}-25
Dentro de las llaves hay unos paréntesis, que son jerárquicamente más importantes que la multiplicación y la suma, por tanto, pasamos ahora a los paréntesis.
=|-3|+4+|4-6|+\left\{5\right(-2)+2\}-25
Realizamos el producto y luego la suma.
=|-3|+4+|4-6|+\{-10+2\}-25
=|-3|+4+|4-6|+\{-8\}-25
Deshacemos las llaves aplicando la ley de signos: \left(+\right)\times \left(-\right)=\left(-\right) .
=\left|-3\right|+4+\left|4-6\right|-8-25
Resolvemos el interior de los valores absolutos. El -3 sale como +3 y 4-6=-2 que sale como +2.
=3+4+2-8-25
Finalmente, vamos por las sumas y restas de izquierda a derecha.
=7+2-8-25
=9-8-25
=1-25
=-24
La respuesta correcta es el inciso d).
Reactivo 4: Lenguaje natural y algebraico
Sean x y y dos números. Si a x le sumas tres unidades y al resultado lo divides entre el doble del segundo número. Como siguiente paso elevas el resultado a la segunda potencia y después le restas el cuarto número natural, considerando al cero. ¿Qué valor debe tener esta operación, si sabemos que x=5 y y=2 ?
- 1
- 2
- 3
- 4
Solución:
Este problema consiste en recrear la expresión matemática que se describe mediante lenguaje natural en el enunciado. Podemos trabajar con x y y para luego sustituir sus valores o hacerlo desde el principio. Lo más recomendable es el primer método, porque así evitamos realizar operaciones de forma incorrecta.
Iremos analizando el enunciado por frases y de esa manera armar la expresión correcta.
Si a x le sumas tres unidades y al resultado lo divides entre el doble del segundo número…
\frac{x+3}{2y}
El segundo número evidentemente es y .
…elevas el resultado a la segunda potencia…
{\left(\frac{x+3}{2y}\right)}^{2}
… y después le restas el cuarto número natural, considerando al cero.
El cuarto número natural, desde cero, sería el 3.
{\left(\frac{x+3}{2y}\right)}^{2}-3
Ahora, sustituimos los valores para a x y y , resolviendo las operaciones correspondientes.
{\left(\frac{5+3}{2\left(2\right)}\right)}^{2}-3={\left(\frac{8}{4}\right)}^{2}-3={\left(2\right)}^{2}-3=4-3=1
El valor de toda la operación es 1.
Concluimos escogiendo como correcta la opción a).
Reactivo 5: Sistema de ecuaciones lineales
José ha ahorrado durante su bachillerato \$20 000 . Como sabe que el próximo año ingresará a la universidad, repartirá su dinero en tres partes, no equitativas, e invertirlo con tres tazas de interés diferentes: 3\%, 5\% y 6\% . El segundo monto es igual al doble del primer monto. Después de haber realizado sus inversiones le dijeron que recibiría de intereses un total de \$1050 . ¿Cuánto invirtió en cada modalidad?
- \$6000 а 3\%,\$3000 a 5\% y 11000 a 6\%
- \$3000 a 3\%,\$11000 a 5\% y 6000 a 6\%
- \$11000 a 3\%,\$6000 a 5\% y 3000 a 6\%
- \$3000 a 3\%,\$6000 a 5\% y 11000 a 6\%
Solución:
Para calcular la fracción de dinero que invirtió (muy inteligentemente) José en las tres tasas de interés, debemos encontrar 3 ecuaciones que nos permitan establecer un Sistema de Ecuaciones Lineales, con la información proporcionada por el enunciado.
A las fracciones de cada tasa de interés las llamaremos:
3\%\to x
5\%\to y
6\%\to z
La primera ecuación que podemos construir, es respecto al dinero que obtiene José luego de recibir los intereses.
1050=0.03x+0.05y+0.06z
Nota: los números escritos en porcentajes son iguales a \frac{\%}{100} .
Además, la suma de las tres fracciones es igual al dinero que tenía José inicialmente.
20000=x+y+z
Por último, el problema nos indica que: el segundo monto es igual al doble del primer monto, es decir:
y=2x
Con esto, ya tenemos 3 ecuaciones y 3 incógnitas para armar el SEL.
\left\{\begin{array}{c}1050=0.03x+0.05y+0.06z \\ 20000=x+y+z\\ y=2x \end{array}\right.
Sustituimos la tercera ecuación en las otras dos, quedando un sistema 2×2.
1050=0.03x+0.05\left(2x\right)+0.06z
1050=0.13x+0.06z
20000=x+2x+z
20000=3x+z
El sistema queda:
\left\{\begin{array}{c}1050=0.13x+0.06z\\ 20000=3x+z\end{array}\right.
Podemos utilizar cualquier método para la solución. En este caso, emplearemos por sustitución. Despejamos a z de la segunda ecuación.
20000=3x+z\to z=20000-3x
Sustituimos en la primera y resolvemos para x .
1050=0.13x+0.06\left(20000-3x\right)
1050=0.13x+1200-0.18x
1200-1050=0.18x-0.13x
\therefore x=3000
Sustituimos este resultado en z=20000-3x .
z=20000-3\left(3000\right)
\therefore z=11000
Calculamos el valor de y .
y=2x\to y=2\left(3000\right)
\therefore y=6000
Finalmente, el dinero invertido en cada modalidad fue:
\$3000 a 3\%,\$6000 a 5\% y 11000 a 6\%
Comparando con las opciones, la respuesta correcta es el inciso d).
Reactivo 6: Sistema de ecuaciones lineales
Sebastián y Gilberto fueron a comprar a la cafetería de la escuela con sus novias. Sebastián pago \$47 por 2 hot dogs y 3 aguas de sabor y Gilberto pago \$48 por 3 hot dogs y 2 aguas. ¿Qué precio tiene cada producto en la cafetería?
- Hot dog\$9, Agua \$10
- Hot dog\$10, Agua \$9
- Hot dog\$8, Agua \$9
- Hot dog\$9, Agua \$9
Solución:
Este problema se resuelve fácilmente empleando un sistema de ecuaciones lineales. Ya que solo tenemos 2 incógnitas: el precio del hot dog y del agua, el sistema tiene que ser de 2×2. A dichas variables nos referiremos como:
Hot dog\to hd
Agua de sabor\to as
Armamos las ecuaciones a partir de la información suministrada por el enunciado.
Sebastián pago \$47 por 2 hot dogs y 3 aguas de sabor…
Sebastian:47=2hd+3as
Gilberto pago \$48 por 3 hot dogs y 2 aguas…
Gilberto:48=3hd+2as
El SEL queda de la siguiente manera:
\left\{\begin{array}{c}47=2hd+3as\\ 48=3hd+2as\end{array}\right.
Puedes utilizar el método que más te guste. Esta vez emplearemos por sustitución. Despejamos a hg de la primera ecuación.
47=2hd+3as\to hd=\frac{47-3as}{2}
Sustituimos en la segunda y simplificamos.
48=3\left(\frac{47-3as}{2}\right)+2as
96=3\left(47-3as\right)+4as
96=141-9as+4as
141-96=9as-4as
as=\frac{45}{5}=9
\therefore as=\$9
Sustituimos este resultado en hd=\frac{47-3as}{2} .
hd=\frac{47-3\left(9\right)}{2}=10
\therefore hd=\$10
Finalmente:
Hot dog\$10, Agua \$9
La respuesta correcta es el inciso b).
Reactivo 7: Sistema de ecuaciones lineales
Resuelve el siguiente sistema de ecuaciones:
0.6x+y+1.5z=380
0.6x+0.9y+1.2z=330
0.2x+0.3y+0.5z=120
- x=200,y=100 y z=100
- x=50,y=50 y z=100
- x=50,y=20 y z=100
- x=50,y=200 y z=100
Solución:
En este caso, tenemos un sistema de 3 ecuaciones con 3 incógnitas. Puedes utilizar cualquier método para encontrar el valor de x, y y z . Esta vez, recurriremos al método por reducción.
Tomaremos la segunda ecuación y la restaremos con la primera.
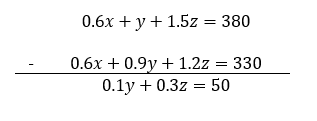
Ahora, restamos la primera ecuación con 3 veces la tercera.
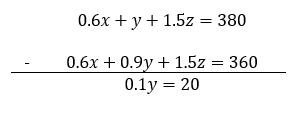
Del resultado anterior podemos despejar directamente a y .
y=\frac{20}{0.1}=200
Esto lo sustituimos en 0.1y+0.3z=50 para obtener a z .
0.1\left(200\right)+0.3z=50\to 0.3z=50-20
\therefore z=100
Finalmente, sustituimos los valores de y y z en cualquiera de las ecuaciones para calcular a x . Seleccionamos la primera ecuación.
0.6x+200+1.5\left(100\right)=380\to 0.6x=380-350
\therefore x=50
Finalmente:
x=50;y=200;z=100
Concluimos que la respuesta correcta es la opción d).
Reactivo 8: Probabilidad de un evento
En una feria se montó una ruleta para lanzar dardos, la cual está dividida en 4 sectores de 48°, 72°, 96° y 144°. Si quiero ganar el premio más grande, debo de ensartar un dardo en el sector que tiene una probabilidad de 0.2\stackrel{-}{6} . ¿A qué sector debo atinar?
- 48°
- 72°
- 96°
- 144°
Solución:
Para calcular la probabilidad de un suceso, en este caso: atinar al sector que tenga por probabilidad 0.2\stackrel{-}{6} , debemos dividir dicho sector desconocido x entre el total del área que tenemos para lanzar. Como el sector es circular, el área total para lanzar es de 360°.
P\left(x\right)=\frac{x}{360°}
Despejamos a x y sustituimos P\left(x\right)=0.2\stackrel{-}{6} . Recordemos que la barra en el 6 significa que es un decimal periódico.
x=360°\left(0.2\stackrel{-}{6}\right)=96°
Debería apuntarle al sector de 96°.
Concluimos seleccionando como respuesta correcta la opción c).
Reactivo 9: Probabilidad conjunta
Al asistir con un tutor te dice que tienes una probabilidad del 65% de aprobar tu curso de probabilidad, 75% de aprobar inglés y 80% para aprobar biología. ¿Cuál es la probabilidad de que apruebes los tres cursos?
- 39
- 58
- 82
- 75
Solución:
Se dice que dos o más sucesos son independientes cuando la probabilidad de ocurrencia de un evento no está condicionada por los demás. En este caso, aprobar un curso no depende de aprobar o reprobar los otros dos, por lo tanto, decimos que los tres son eventos independientes.
Ahora, para calcular la probabilidad conjunta de eventos independientes, se utiliza la regla de la multiplicación.
P\left(A\cap B\right)=P\left(A\right)\bullet P\left(B\right)
Asociemos al hecho de aprobar cada curso una letra: A para probabilidad, B para inglés y C para biología; calculamos la probabilidad de aprobar las tres asignaturas como:
P\left(A\cap B\cap C\right)=P\left(A\right)\bullet P\left(B\right)\bullet P\left(C\right)
Si: P\left(A\right)=0.65 , P\left(B\right)=0.75 y P\left(C\right)=0.8 , entonces:
P\left(A\cap B\cap C\right)=\left(0.65\right)\left(0.75\right)\left(0.8\right)=0.39
La probabilidad de aprobar los tres cursos es del 39%.
Concluimos el reactivo escogiendo la opción a) como respuesta correcta.
Reactivo 10: Técnicas de conteo
¿Cuántas placas diferentes se generan si constan de tres números y 3 letras? Para la fabricación se utilizan 10 dígitos y 27 letras.
- 19 683 000
- 2 598 561 265
- 25 365
- 258 698
Solución:
El problema solicita que calculemos la cantidad de placas que se pueden grabar con códigos alfanuméricos formados por 3 números y 3 letras. En primera instancia, podemos identificar que sí importa el orden, ya que, por ejemplo, 2N4M6Z es diferente a N24M6Z. Debemos emplear permutaciones o variaciones.
Ahora, los números van del 0 al 9 y las letras de la A hasta la Z; debido a que ambos conjuntos solo se emplean de 3 en 3, no intervienen todos los elementos. Debemos recurrir a las variaciones.
Una última consideración, es respecto a si se pueden o no repetir elementos. El enunciado no indica nada al respecto, por lo que es posible repetirlo. Debemos utilizar la fórmula la variación con repetición:
{VR}_{m,n}={m}^{n}
La fórmula anterior aplica para las combinaciones de un solo conjunto. Para calcular la cantidad de placas, debemos aplicar el principio multiplicativo:
Placas={VR}_{\mathrm{10,3}}\times {VR}_{\mathrm{27,3}}=\left({10}^{3}\right)\left({27}^{3}\right)
\therefore Placas=19 683 000
Concluimos seleccionando como correcta la opción a).

