¡Hola aspirante! En este tutorial resolveremos la primera parte los reactivos de la guía de ingreso CSH sobre Razonamiento Matemático para el examen de la UAM. Específicamente, trataremos con los ejercicios del 26 al 38.

No olvides resolver los problemas por tu cuenta antes de mirar el desarrollo. Obtener una buena calificación depende del tiempo que dediques a tu preparación.
Resumen de la convocatoria UAM 2022.
- Número de convocatorias: Dos al año.
- Fechas de registro: marzo y agosto del 2022
- Oferta académica: 82 carreras
- Divisiones académicas: 6
- Modalidad: en línea
Estructura del examen de ingreso UAM 2022
El examen de ingreso está dividido en dos grandes partes:
- La prueba de aptitud
- La prueba de conocimientos específicos
La primera tiene reactivos de razonamiento matemático (como los de esta guía) y sobre razonamiento verbal. Por otro lado, la segunda parte, denominada conocimientos específicos, depende de la división de tu carrera.
En el caso de CSH las asignaturas son: literatura, historia, formación cívica y política, filosofía y matemáticas.
La siguiente lista, contiene un resumen de los sub temas incluidos en las asignaturas ya mencionadas.
Literatura
- El lenguaje literario.
- Los géneros literarios.
- Principales autores literarios hispanos y latinoamericanos.
Historia de México
- Mesoamérica.
- Independencia.
- La República Liberal.
- La República Restaurada.
- El Porfiriato.
- La Revolución.
- México posrevolucionario.
Historia universal
- Civilizaciones antiguas: Grecia y Roma.
- Feudalismo.
- Renacimiento.
- Expansión europea.
- Revolución industrial y revoluciones burguesas.
- Antecedentes y consecuencias de las conflagraciones mundiales del Siglo XX.
- Descolonización y democratización.
Formación cívica y política
- Organización política.
- Sistema político mexicano.
- Organización social.
Filosofía
- Principales problemas filosóficos.
- La evolución de las cuestiones y perspectivas filosóficas.
- Lógica.
Matemáticas.
- Aritmética.
- Álgebra.
- Geometría Plana.
- Geometría Analítica.
Resumen de reactivos en cada parte del examen.
| Área | Reactivos | Porcentaje |
|---|---|---|
| Razonamiento verbal | 20 | 25% |
| Razonamiento matemático | 20 | 25% |
| Conocimientos específicos | 40 | 50% |
| Total | 80 | 100% |
Temario de Raz. Matemático para CSH
El siguiente, es un resumen de todos los temas incluidos en Razonamiento Matemático del examen de ingreso a la UAM. Ten en cuenta que este temario aplica para el resto de divisiones.
- Completar series lógicas o con elementos abstractos.
- Identificación de relaciones causales.
- Identificación de elementos gráficos.
- Identificación del todo y sus partes y las relaciones entre ellas.
- Razonamiento inductivo y deductivo.
- Resolver problemas rutinarios.
- Conocimientos específicos
- Razonamiento numérico
Guía UAM CSH Raz. Matemático parte 1
Luego de esta introducción, en la que hemos recordado la estructura y temario del examen, pasamos con la solución paso a paso de los ejercicios de Razonamiento Matemático para la UAM.
Reactivo 26: Sucesiones numéricas
En las sucesión numérica 8, 7, 11, 10, 14,…, los dos números siguientes son:
- 13, 16
- 18, 14
- 13, 17
- 18, 17
- 15, 18
Solución:
Para encontrar los números faltantes de la sucesión, debemos identificar la regla con la que cambian.
La sucesión inicia en 8 y luego disminuye 1 por tanto, el segundo término es 7. El tercer término incrementa en 4 unidades respecto al segundo, pasa de 7 a 11 y el cuarto vuelve a disminuir en 1, quedando ahora en 10.
El quinto término incrementa nuevamente en 4 unidades, pasa de 10 a 14. Esto ya nos da una clara idea de la regla que sigue la sucesión.
Decrece 1, incrementa 4, decrece 1, incrementa 4,…
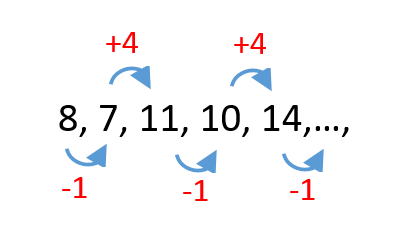
De esta forma, el sexto elemento debe disminuir en 1, es decir 13 y el séptimo debe incrementar en 4, es decir 17.
8, 7, 11, 10, 14, 13, 17,…
Comparando con las opciones, la respuesta correcta es la opción C.
Reactivo 27: Sucesiones numéricas
En la sucesión numérica 75, 74, 72, 71,… los dos números siguientes son:
- 69, 71
- 69, 67
- 68, 67
- 69, 68
- 15, 18
Solución:
Procedemos a identificar la regla que hace cambiar a los números de la sucesión. El primer término es 75, que disminuye 1 para que el segundo sea 74.
El tercer término es 72, por lo que disminuyó dos unidades para pasar del segundo al tercero. El cuarto término vuelve a disminuir en uno y se coloca en 71. La regla en esta sucesión es:
Disminuye 1, disminuye 2, disminuye 1, disminuye 2,…
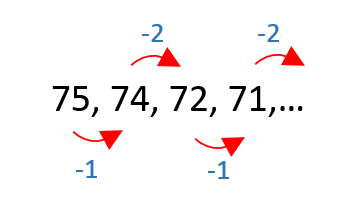
En base a esto, el quinto término debe disminuir dos respecto al cuarto, es decir 69 y el sexto 1 respecto al quinto, 68.
75, 74, 72, 71, 69, 68,…
Comparando con las opciones, concluimos seleccionando a la D como la respuesta correcta.
Reactivo 28: Sucesiones numéricas
En la sucesión numérica 6, 18, __, 360, 2160, el número que falta es:
- 48
- 72
- 54
- 36
- 90
Solución:
En esta sucesión, el incremento entre términos es brusco. Eso nos indica que la regla de cambio entre términos sucesivos es un producto o una potencia.
La sucesión inicia en 6, el segundo término es 18 que se obtiene al multiplicar por 3 al primero:
{a}_{2}=3*{a}_{1}=3*6=18
El tercer término es desconocido. El quinto término puede obtenerse al multiplicar el cuarto término por 6:
{a}_{5}=6*{a}_{4}=6*360=2160
Esto por ahora no dice mucho, pero podemos descomponer al primer término como:
{a}_{1}=2*3=6
Escribamos cada término uno debajo del otro.
{a}_{1}=2*3=6
{a}_{2}=3*{a}_{1}=18
{a}_{3}=?
{a}_{4}=360
{a}_{5}=6*360
Si observamos con detenimiento, el primero es 2 por 3, el segundo 3 por el primero,… el quinto 6 por el cuarto. Es decir, el siguiente elemento se consigue al multiplicar el anterior por la posición del siguiente más 1.
{a}_{n}=\left(n+1\right){a}_{n-1}
De esta forma, el tercer elemento debería ser 4 multiplicado por el segundo:
{a}_{3}=4*{a}_{2}=4*18=72
Esto lo podemos rectificar, si obtenemos al cuarto elemento como el tercero multiplicado por 5:
{a}_{4}=5*{a}_{3}=5*72=360
En efecto, esta es la regla de la sucesión. Completando nos queda:
6, 18, 72, 360, 2160,…
Comparando con las opciones, seleccionamos como correcta a la B.
Reactivo 29: Sucesiones numéricas
En la sucesión numérica 9, 17, 11, 19,…, el número siguiente es:
- 11
- 13
- 15
- 22
- 27
Solución:
Para determinar la regla que rige a la sucesión, debemos examinar en qué cantidades varían unos términos respecto de otros.
La sucesión inicia en 9, el segundo término se obtiene sumando 8 al primero 9+8=17 , el tercero restando 6 al segundo 17-6=11 y el cuarto sumando 8 al tercero 11+8=19 .
Con este rápido análisis es evidente que la regla de la sucesión es:
Sumar 8, restar 6, sumar 8, restar 6,…
Por tanto, el quinto término se obtiene restando 6 al cuarto término:
{a}_{5}=19-6=13
La serie quedaría como:
9, 17, 11, 19, 13,…
La respuesta correcta es la B.
Reactivo 30: Sucesiones numéricas
En la sucesión numérica 13, 18, 24, 29,…, los dos números que siguen son:
- 34, 39
- 34, 41
- 35, 40
- 35, 39
- 35, 41
Solución:
Identificamos la regla que rige a la sucesión analizando cuánto crece un término respecto de otro.
La sucesión inicia en 13; el segundo término es 5 unidades mayor al primero 13+5=18 , el tercero es 6 unidades mayor al segundo 18+6=24 y el cuarto término 5 unidades mayor que el tercero 24+5=29 .
En base al análisis anterior, determinamos que la regla es:
Sumar 5, sumar 6, sumar 5,…
Por tanto, si en el cuarto término se sumaron 5 para el quinto toca sumar 6:
{a}_{5}=29+6=35
Para el sexto toca sumar 5:
{a}_{6}=35+5=40
La sucesión con dos términos más queda como:
13, 18, 24, 29, 35, 40,…
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 31: Series lógicas con letras
Selecciona la opción que ROMPE la regularidad.
- DEFG
- KLMN
- PQRS
- WXYZ
- HIKL
Solución:
Debemos inspeccionar las secuencias de letras en cada inciso y determinar cómo cambian, aquella que lo haga de forma distinta al resto, será la que ROMPE con la regularidad.
En los dos primeros incisos, las secuencias de letras tienen el mismo orden que en el abecedario.
A B C \underset{A}{\underset{⏟}{D E F G}} H I J \underset{B}{\underset{⏟}{K L M N}} Ñ O P Q R S T U V W X Y Z
De igual forma para los incisos C y D.
A B C \underset{A}{\underset{⏟}{D E F G}} H I J \underset{B}{\underset{⏟}{K L M N}} Ñ O \underset{C}{\underset{⏟}{P Q R S}} T U V \underset{D}{\underset{⏟}{W X Y Z}}
Esto no es así en la secuencia del inciso E, ya que la secuencia se rompe al pasar de la “I” a la “K”, en lugar de pasar a la “J”. Concluimos indicando que la respuesta correcta es la opción E.
Reactivo 32: Códigos alfanuméricos
Si se traducen las letras y número a otro código se puede obtener una interpretación nueva. Elige la opción que da sentido al conjunto de caracteres.
LX 9X7W1X 3S 9W163WO
- AL PRIMER PATRIOTA
- LO PRIMERO ES ULTIMO
- MI FRASE NO ENTIENDO
- LA PATRIA ES PRIMERO
- SE MEJORA EL CONSUMO
Solución:
Analizando la frase que se encuentra “encriptado”, podemos intuir que la “L” de la primera palabra, la “S” en la tercera y la “O” al final de la cuarta quedan iguales y nos ayudarán a darle sentido a la frase real.
En base a lo anterior, los incisos A, C y E se pueden descartar porque no comienzan por la letra “L”. Solo quedan la B y la D.
Ahora, contemos la cantidad de letras en cada palabra, si alguna en uno de los incisos difiere en número de letras con la frase dada, la misma queda descartada y automáticamente la otra sería la correcta.
\underset{2}{\underset{⏟}{LX}} \underset{6}{\underset{⏟}{9X7W1X}} \underset{2}{\underset{⏟}{3S}} \underset{7}{\underset{⏟}{9W163WO}}
Inciso B:
\underset{2}{\underset{⏟}{LO}} \underset{7}{\underset{⏟}{PRIMERO}} \underset{2}{\underset{⏟}{ES}} \underset{6}{\underset{⏟}{ULTIMO}}
El inciso B difiere en una letra en la segunda palabra y en la cuarta, por tanto la correcta es la frase del D.
LA PATRIA ES PRIMERO=LX 9X7W1X 3S 9W163WO
Otra forma de comprobar la respuesta, es que las letras ocupen semánticamente el mismo lugar en cada palabra.
LA PATRIA ES PRIMERO
LX 9X7W1X 3S 9W163WO
La X siempre ocupa el lugar de la A, el 9 el de la P, el 7 el de la T, la W el de la R y así con el resto. Concluimos indicando como respuesta correcta la opción D.
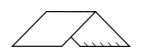
Reactivo 33: Figuras y dobleces
¿Qué se obtiene al doblar la siguiente figura por la línea punteada?
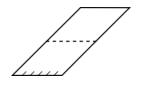
Solución:
Antes de comenzar a analizar los dobleces, debemos señalar dos cosas:
- No se nos indica el sentido en que se dobla el pliegue (hay que probar ambos)
- La figura no está siendo doblada por su eje de simetría, por tanto, no pueden quedar solapadas las dos caras. Esto descarta en primera instancia la opción B
Solo nos queda imaginar el desdobles de cada figura en ambos sentidos, si la figura desdoblada es igual a la del enunciado entonces esa es la respuesta correcta.
Figura A.
Si se desdobla la cara de adelante, la figura queda:
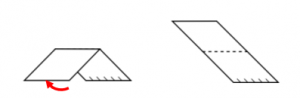
Desdoblando la cara cubierta (la del borde punteado):
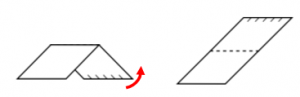
Ninguna corresponde.
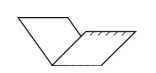
Figura C.
Desdoblando cara delantera:
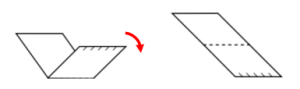
Desdoblando cara trasera:
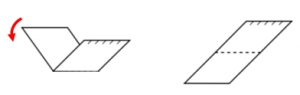
Figura D.
Sucede lo mismo que en la figura A.
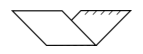
Figura E.
Desdoblando cara delantera:

Desdoblando cara trasera:
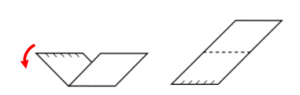
En base al resultado final, concluimos seleccionando a la opción E como la respuesta correcta.
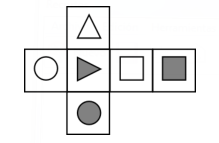
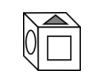
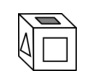
Reactivo 34: Cubos y patrones
El siguiente desarrollo corresponde al volumen:
Solución:
Para relacionar el patrón con uno de los cubos en los incisos, primero debemos “armar” y dejar frente a nosotros la cara con el cuadrado vacío.
Hagámonos ahora una idea de cómo han quedado el resto de caras. Si el rectángulo vacío está en frente, la cara con el círculo vacío estaría detrás de ella y en la superior puede estar el cuadro relleno o el triángulo relleno.
Con el cuadro relleno arriba, a la izquierda queda el triángulo vacío. Si el triángulo relleno queda en la parte superior, a la izquierda debe estar el círculo relleno.
Incisos con triángulo en la cara superior:
Inciso E.
Esta no corresponde, ya que a la izquierda debe estar el círculo relleno.
Incisos con rectángulo en la cara superior:
Inciso A.
Este es el cubo correcto, ya que el triángulo vacío está en la cara izquierda.
Concluimos que la respuesta correcta es el inciso A.
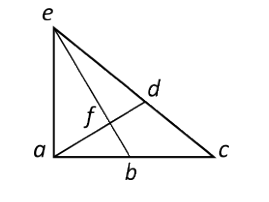
Reactivo 35: Triángulos internos
¿Cuál es el número máximo de triángulos distintos que puedes encontrar en la siguiente figura?
- 5
- 6
- 7
- 8
- 9
Solución:
Debemos identificar todos los triángulos diferentes que se encuentran en la figura. Consideraremos diferentes a los triángulos que tengan distinta combinación de vértices. Comenzaremos por el triángulo externo y luego por los más internos.
Triángulo externo: ace.
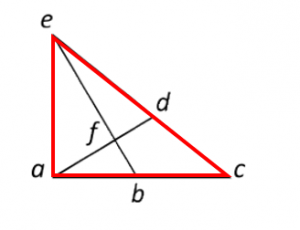
Triángulo abe:
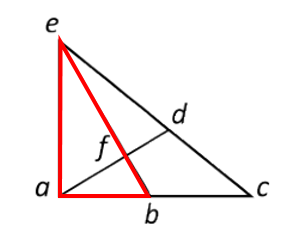
Triángulo bce:
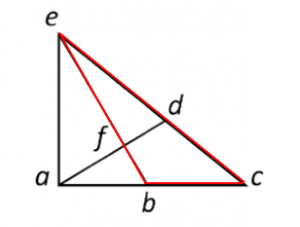
Triángulo ade:
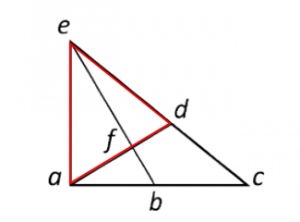
Triángulo adc:
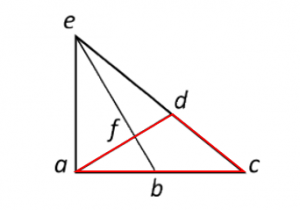
Triángulo afe:
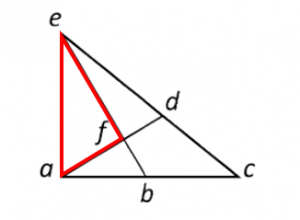
Triángulo fde:
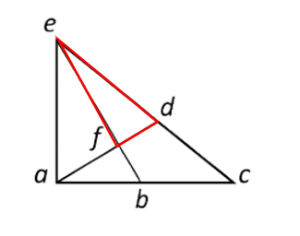
Triángulo afb:
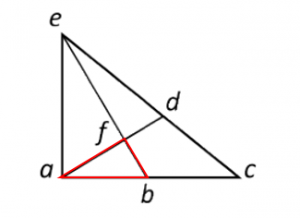
En total, hay 8 triángulos distintos en la figura. Concluimos indicando como respuesta correcta a la opción D.
Reactivo 36: Figuras tridimensionales
Si formas un tetraedro a partir de un triángulo equilátero ¿Cuántos triángulos equiláteros menores obtienes?
- 2
- 3
- 4
- 5
- 6
Solución:
Un tetraedro formado por triángulos equiláteros es denominado tetraedro regular, sus 4 caras son iguales y corresponden a triángulos equiláteros. Por este motivo, no hay triángulos menores (o mayores) ya que todos son iguales.
En base a lo anterior, seleccionamos como respuesta correcta a la opción C: 4 triángulos equiláteros.
Reactivo 37: Fracciones y proporciones
Una botella tiene una capacidad total de \frac{9}{5} litros y contiene aceite en \frac{5}{9} de su capacidad ¿Cuánto aceite, en litros, hay en la botella?
- 0.555
- 1
- \frac{56}{45}
- \frac{25}{81}
- \frac{81}{25}
Solución:
Para calcular los litros de aceite que tiene la botella, debemos hacer el producto de la fracción en la que se encuentra llena la botella, es decir \frac{5}{9} por la capacidad en litros de la botella, en este caso \frac{9}{5} litros.
Litros de aceite=\frac{9}{5}l*\frac{5}{9}=1 litro
Cuando la botella está a \frac{5}{9} de su capacidad total, alberga 1 litro de aceite. Comparando con las opciones, seleccionamos como correcta a la opción B.
Reactivo 38: Problemas con fracciones
En un grupo de 60 alumnos, cierto día \frac{1}{10} del grupo es atacado por una infección; \frac{2}{3} de los infectados deciden permanecer en cama, mientras que el resto de todo el grupo asiste a clase. El número de alumnos que asistieron a clase es:
- 6
- 40
- 54
- 56
- 58
Solución:
En base a lo que nos dice el enunciado, de los estudiantes infectados \frac{2}{3} decide quedarse en casa, por tanto \frac{1}{3} asiste a clases junto al grupo que no ha sido infectado.
El número total de estudiantes que asistieron se calcula como la suma de la fracción de infectados que decidió asistir más el resto de estudiantes que no fueron infectados:
Estudiantes que asistieron=Infectados que asistieron+No infectados
Los no infectados es el restante a \frac{1}{10} , es decir \frac{9}{10} :
No infectados=60*\frac{9}{10}=54
Ahora, calculamos el total de infectados y a ese resultado lo multiplicamos por la fracción de infectados que asistieron, es decir \frac{1}{3} .
Infectados=60*\frac{1}{10}=6
Infectados que asistieron=6*\frac{1}{3}=2
Sustituimos:
Estudiantes que asistieron=2+54=56
El número de alumnos que asistieron a clase es: 56
Comparando con las opciones, seleccionamos como correcta a la D.