¡Hola aspirante! Ahora vamos con la solución de la segunda y última parte la guía de ejercicios de Razonamiento Matemático para la división de Ciencias Biológicas y de la Salud de la Universidad Autónoma Metropolitana. Los reactivos van desde el 38 hasta el 50.

Guía UAM Razonamiento Matemático Parte 2
Te invito a continuar aprendiendo sobre razonamiento matemático, física, química y biología con el resto de guías que tenemos en Unibetas Pro para ti.
Reactivo 38: Porcentajes
Un banco da el 5% de interés semestral ¿Cuánto esperas tener en el banco en un año si depositaste $1000.00 y no retiraste los intereses?
- $1 050.00
- $1 102.50
- $1 100.00
- $1 210.50
- $1. 100.50
Solución:
El 5% de intereses semestral implica que cada seis meses, el saldo en la cuenta bancaria aumenta un 5%, si la proyección se realiza para un año en los primeros 6 meses se obtiene un 5% del saldo, es decir:
\$1000.00*105\%=\$1050.00
Al finalizar el segundo semestre del año, se obtiene el otro 5% en intereses. Debemos calcular el 105% del saldo acumulado que, como no hubo ningún retiro y suponemos tampoco otro ingreso externo se mantiene en $1 050.00.
\$1050.00*105\%=\$1102.5
Comparando con las opciones, escogemos a B como la respuesta correcta.
Reactivo 39: Semejanzas entre triángulos
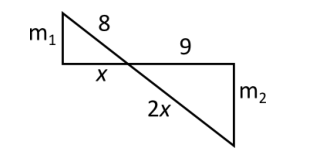
En la siguiente figura los segmentos {m}_{1} y {m}_{2} están sobre rectas paralelas ¿Cuál es el valor de x ?
- \frac{9}{2}
- 4
- \frac{2}{9}
- 6
- 3\sqrt{2}
Solución:
Aunque a simple vista no lo parezca, ambos triángulos son semejantes porque la hipotenusa tiene el mismo ángulo de inclinación respecto a la horizontal. Debemos aplicar lados homólogos de semejanza de triángulos para encontrar a x .
Son homólogos entre sí: las hipotenusas, los lados paralelos y las bases.
\frac{8}{2x}=\frac{x}{9}=\frac{{m}_{1}}{{m}_{2}}
Nos conviene utilizar la igualdad \frac{8}{2x}=\frac{x}{9} ya que aquí, la única incógnita es la x . Despejamos.
\frac{8}{2x}=\frac{x}{9}\to 8*9=2{x}^{2}
x=\sqrt{\frac{54}{2}}=6
El valor de x es 6.
Comparando con las opciones, la respuesta correcta es la D.
Reactivo 40: Diagonales de un polígono
Si en un polígono se trazan desde un solo vértice todas las diagonales posibles, se observa que el número de diagonales es igual al número de lados:
- Menos dos
- Menos tres
- Más tres
- Más dos
- Más cuatro
Solución:
En un polígono regular, el número de vértices es igual al número de lados.
v=l
Además, las diagonales que se pueden trazar desde un mismo vértice es igual al número de vértices (o lados) menos tres, ya que un vértice no puede trazar una diagonal consigo mismo ni con los dos vértices contiguos con los que está conectado.
Concluimos que:
El número de diagonales es igual al número de lados menos tres.
Comparando con las opciones, la correcta corresponde con la B.
Reactivo 41: Relaciones entre ángulos
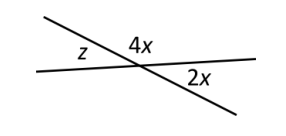
En el siguiente diagrama ¿Cuál es el valor en grados del ángulo z ?
- 80°
- 60°
- 100°
- 30°
- 40°
Solución:
Para calcular el valor de z debemos aplicar las relaciones entre ángulos opuestos por el vértice y ángulos suplementarios (que suman 180°). A partir de la imagen, sabemos que z y 2x son opuestos por el vértice y cumplen la siguiente igualdad.
z=2x
Por otro lado, 2x y 4x son suplementarios (suman 180°):
2x+4x=180
De esta última ecuación despejamos a x .
6x=180\to x=30°
Finalmente, sustituimos en la primera ecuación:
z=2x\to z=2\left(30°\right)
\therefore z=60°
Comparando con las opciones, la respuesta correcta es la B.
Reactivo 42: Triángulos internos
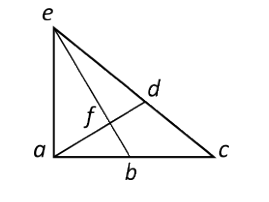
¿Cuál es el número máximo de triángulos distintos que puedes encontrar en la siguiente figura?
- 5
- 6
- 7
- 8
- 9
Solución:
Debemos identificar todos los triángulos diferentes que se encuentran en la figura. Consideraremos diferentes a los triángulos que tengan distinta combinación de vértices. Comenzaremos por el triángulo externo y luego por los más internos.
Triángulo externo: ace.
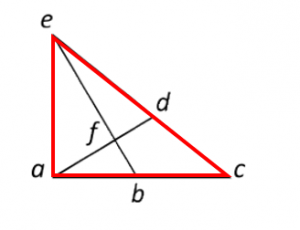
Triángulo abe:
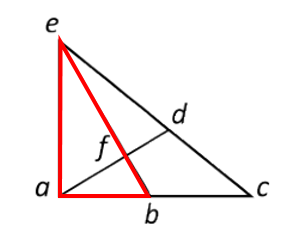
Triángulo bce:
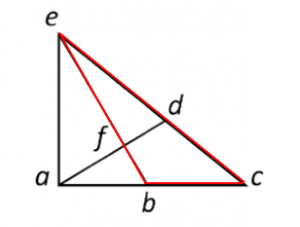
Triángulo ade:
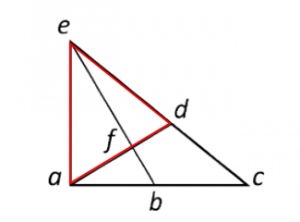
Triángulo adc:
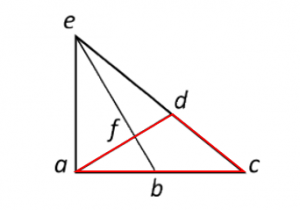
Triángulo afe:
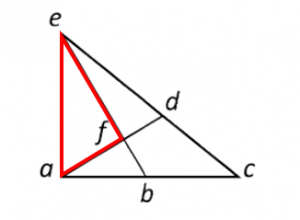
Triángulo fde:
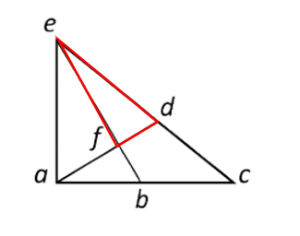
Triángulo afb:
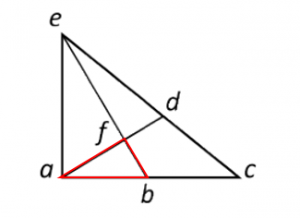
En total, hay 8 triángulos distintos en la figura. Concluimos indicando como respuesta correcta a la opción D.
Reactivo 43: Relaciones entre ángulos
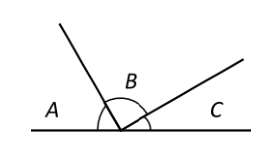
Si A es el doble de C y B es el triple de C, encuentra el valor del ángulo A.
- 40°
- 45°
- 50°
- 60°
- 70°
Solución:
Para calcular el valor de A, debemos convertir en ecuaciones las relaciones dadas por el ejercicio, además de aplicar ángulos suplementarios.
A es el doble de C…
A=2C \left(1\right)
…B es el triple de C…
B=3C \left(2\right)
Los tres ángulos A, B y C son suplementarios:
A+B+C=180° \left(3\right)
Despejamos a C de la primera ecuación.
A=2C\to C=\frac{A}{2}
Sustituimos el resultado en la segunda.
B=\frac{3A}{2}
Por último, se deja a la tercera ecuación en términos de A.
A+B+C=180°\to A+\frac{3A}{2}+\frac{A}{2}=180
A+2A=180\to A=\frac{180}{3}=60°
El ángulo A tiene un valor de 60°.
Finalizamos seleccionando como respuesta correcta a la opción D.
Reactivo 44: Figuras tridimensionales
Si formas un tetraedro a partir de un triángulo equilátero ¿Cuántos triángulos equiláteros menores obtienes?
- 2
- 3
- 4
- 5
- 6
Solución:
Un tetraedro formado por triángulos equiláteros es denominado tetraedro regular, sus 4 caras son iguales y corresponden a triángulos equiláteros. Por este motivo, no hay triángulos menores (o mayores) ya que todos son iguales.
En base a lo anterior, seleccionamos como respuesta correcta a la opción C: 4 triángulos equiláteros.
Reactivo 45: Simplificación de expresiones
¿Cuál de las siguientes expresiones es cierta para cualquier valor de a no nulo?
- 20a÷5{a}^{2}=4a
- 20{a}^{2}÷5a=4a
- 20{a}^{2}÷5a=4{a}^{2}
- {20}^{2}a÷5{a}^{2}=4a
- {20}^{2}a÷5a=4a
Solución:
Para encontrar la respuesta correcta, debemos simplificar el primer miembro de cada ecuación y comprobar que se cumpla la igualdad.
Primera ecuación:
20a÷5{a}^{2}=4a\to \frac{20a}{5{a}^{2}}=4a
\frac{4}{a}=4a
No cumple la igualdad
Segunda ecuación:
20{a}^{2}÷5a=4a\to \frac{20{a}^{2}}{5a}=4a
4a=4a
Cumple la igualdad.
Tenemos como posible respuesta correcta a la B, es necesario comprobarlas todas.
Tercera ecuación:
20{a}^{2}÷5a=4{a}^{2}\to \frac{20{a}^{2}}{5a}=4{a}^{2}
4a=4{a}^{2}
No cumple la igualdad.
Cuarta ecuación:
{20}^{2}a÷5{a}^{2}=4a\to \frac{{20}^{2}a}{5{a}^{2}}=4a
\frac{80}{a}=4a
No cumple la igualdad
Quinta ecuación:
{20}^{2}a÷5a=4a\to \frac{{20}^{2}a}{5a}=4a
80=4a
No cumple la igualdad.
En definitiva, la respuesta correcta es la opción B.
Reactivo 46: Lenguaje natural a lenguaje algebraico
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera más el duplo de la primera por la segunda más el cuadrado de la segunda ¿Cuál de las siguientes expresiones algebraicas siguientes representa lo anterior?
- (a+b{)}^{2}={a}^{2}+2ab-{b}^{2}
- (a+b{)}^{2}=2{a}^{2}+ab+{b}^{2}
- (a+b{)}^{2}={a}^{2}+ab+2{b}^{2}
- (a+b{)}^{2}={a}^{2}+2ab+{b}^{2}
- (a+b{)}^{2}={a}^{2}-2ab-{b}^{2}
Solución:
Debemos transformar cada una de las frases a su expresión matemática equivalente. Para ello, analizaremos parte por parte.
El cuadrado de la suma de dos cantidades…
{\left(a+b\right)}^{2}
Ya que las respuestas utilizan a y b para representar a las cantidades, haremos lo mismo para mantener concordancia; pero pueden ser cualesquiera letras del abecedario.
…es igual al cuadrado de la primera…
{\left(a+b\right)}^{2}={a}^{2}
Hemos escogido como primera a la letra a .
…más el duplo de la primera por la segunda…
{\left(a+b\right)}^{2}={a}^{2}+2ab
“El duplo” es sinónimo de “el doble” o “dos veces”.
…más el cuadrado de la segunda.
{\left(a+b\right)}^{2}={a}^{2}+2ab+{b}^{2}
Esta ecuación es igual al producto notable para el cuadrado de la suma de dos cantidades.
Comparando con las opciones, la respuesta correcta es la D.
Reactivo 47: Problemas con sistemas de ecuaciones
Un hacendado ha comprado el doble del número de gallos que de bueyes. Por cada gallo pago $70 y por cada buey $85 y el importe total de la compra fue de $2700. Si x es la cantidad de bueyes ¿Qué ecuación permite calcularla?
- 85x+70x=2700
- 170x+140x=2700
- 85x+140x=2700
- 85x+35x=2700
- 170x+70y=2700
Solución:
Para resolver el problema, debemos identificar (a partir del enunciado) las relaciones entre las variables y con ellas armar un sistema de ecuaciones.
La primera relación la encontramos en la frase: ha comprado el doble del número de gallos que de bueyes… Si la cantidad de bueyes es x y la de gallos y , esto se escribiría en ecuación como:
y=2x
Nos indican además cuánto ha pagado por cada animal junto al total del importe:
85x+70y=2700
El número de bueyes multiplicado por su precio, más el número de gallos también multiplicados por el precio es igual al total de la compra. Sustituimos y=2x en la segunda ecuación.
85x+70\left(2x\right)=2700
85x+140x=2700
Comparando el resultado con las opciones, concluimos escogiendo como correcta a la opción C.
Reactivo 48: Problemas con sistemas de ecuaciones
Si la edad de Pedro es el doble que la de Juan y hace 20 años la edad de Pedro era el triple que la de Juan ¿Qué ecuación permite calcular la edad de Juan?
- 2x-20=3\left(x-20\right)
- 2x-20=3\left(x+20\right)
- 2x-20=3x+20
- 2x-20=3x-20
- x-20=x+20
Solución:
Comencemos por pasar a ecuaciones las relaciones entre las edades de Juan x y Pedro y establecidas por el problema.
…la edad de Pedro es el doble que la de Juan…
y=2x
…hace 20 años la edad de Pedro era el triple que la de Juan…
Comencemos por establecer la igualdad al final.
y=3x
Como fue hace 20 años, debemos restarle a la edad de Juan y Pedro 20 años.
y-20=3\left(x-20\right)
Ahora, sustituimos la primera ecuación en la segunda.
2x-20=3\left(x-20\right)
Comparando con las opciones, seleccionamos como respuesta correcta a la opción A.
Reactivo 49: Problemas matemáticos
Expresa 85 como la suma de dos sumandos tales que el triple del menor equivalga al doble del mayor, ¿Qué ecuación permite resolver el problema?
- 3x-2=2\left(85-x\right)
- 3x=2\left(85-x\right)
- 3x=2\left(85+x\right)
- 3-x=2\left(85-x\right)
- 2\left(3x\right)=2\left(85-x\right)
Solución:
En este caso, las dos cantidades serán x y y . De la primera frase, sabemos que ambas deben sumar 85, esto se escribe como:
x+y=85
Ahora, diremos que x es la cantidad menor y y la cantidad mayor. Continuando con el fragmento: …el triple del menor equivale al doble del mayor… establecemos que:
3x=2y
Despejamos de la primera ecuación a y y sustituimos la expresión resultante en la segunda.
x+y=85\to y=85-x
Sustituyendo:
3x=2\left(85-x\right)
Comparando con las opciones, seleccionamos como correcta a la B.
Reactivo 50: Problemas con sistemas de ecuaciones
Lidia compró cierto número de sacos de frijoles por la cantidad de $240. Si ella hubiera comprado 3 sacos más por el mismo dinero, cada saco le habría costado $4 menos, ¿Qué ecuación permite calcular el precio x de un saco de frijoles?
- \left(\frac{240}{x}+3\right)\left(x-4\right)=240
- \frac{240}{x}=\frac{240}{x+3}-3
- \frac{240}{x}=\frac{240}{x+3}-4
- 240x=240\left(x+3\right)-4
- 240x=\frac{x+3}{240}+4
Solución:
Debemos identificar las variables del problema para establecer un sistema de ecuaciones. Llamaremos al precio de un saco de frijol x y a la cantidad de sacos de frijoles y .
A partir de la frase Lidia compro cierto número de sacos de frijoles por la cantidad de $240 sabemos que:
y*x=240
El número de sacos por su precio unitario es igual a $240.
En la siguiente frase: si ella hubiera comprado 3 sacos más por el mismo dinero, cada saco le habría costado $4 menos, sabemos que a la anterior cantidad de sacos le sumamos 3, pero al precio por saco le restamos $4.
\left(y+3\right)\left(x-4\right)=240
Ahora tenemos 2 ecuaciones con dos incógnitas. Ya que necesitamos el precio por saco x , despejamos a y de la primera ecuación para sustituirla en la primera.
y=\frac{240}{x}
Sustituimos.
\left(\frac{240}{x}+3\right)\left(x-4\right)=240
Esta ecuación permite calcular el precio x de un saco de frijoles.
Comparando con las opciones, seleccionamos como correcta a la opción A.


