¡Felicidades aspirante! Vamos con la segunda y última parte de la guía resuelta de Matemáticas para la división de Ciencias Sociales y Humanidades (CSH) de la UAM, donde estaremos desarrollando los ejercicios desde el 100 hasta el 110.

Guía UAM CSH Matemáticas parte 2
Pasamos finalmente con la solución paso a paso de los reactivos de matemáticas para la división de Ciencias Sociales y Humanas, en el examen de ingreso a la UAM.
Reactivo 100: Logaritmos
Si {2}^{3}=8 entonces:
- 3=8
- 3=2
- 2=3
- 8=3
- 8=2
Solución:
Este problema podemos resolverlo fácilmente aplicando la definición de logaritmo. Si la división es la operación inversa a la multiplicación, el logaritmo lo es para la potenciación. Dado un número a elevado a una potencia n , su resultado será x .
{a}^{n}=x
Con el logaritmo encontramos al número n al que debemos elevar a la base a para obtener como resultado a x .
x =n
Esto se lee como: el logaritmo base a de x es igual a n .
{a}^{n}=x\to x =n
En base al problema planteado por el enunciado a=2 , n=3 y x=8 , escrito en forma de logaritmo quedaría:
{2}^{3}=8\to 8 =3
Comparando con las opciones, la respuesta correcta es la A.
Reactivo 101: Ecuaciones con logaritmos
La solución de la ecuación {log}_{2}x=4 es:
- x=4\left(2\right)
- x={2}^{2}
- x=2
- x={4}^{2}
- x={2}^{4}
Solución:
Las ecuaciones con logaritmos se resuelven aplicando las propiedades más adecuadas, según sea el caso. Esta vez, solo basta con recurrir a la definición de logaritmo.
{a}^{n}=b\to b =n
Aplicada en sentido inverso, podemos expresar {log}_{2}x=4 como una potencia:
{2}^{4}=x
Como las opciones están escritas como potencias, no es necesario simplificar {2}^{4} .
Comparando con los incisos, la respuesta correcta se encuentra en el E.
Reactivo 102: Desigualdades
Si m>n , el resultado de \sqrt{mn} es:
- Menor que n
- Mayor que m
- Menor que m
- Igual a n
- Igual a m
Solución:
En este caso, debemos aplicar algunos trucos para obtener de un lado de la desigualdad \sqrt{mn} y del otro la expresión correspondiente a la respuesta del ejercicio. Primero, multiplicamos en ambos lados por m .
{m}^{2}>nm
Aclaramos que el sentido de la desigualdad solo se mantiene para m y n>0 ó m y n<0 . Además, si no se cumple una de las dos condiciones anteriores no podríamos aplicar raíz par, porque el producto mn sería negativo y sin raíz de índice par en los reales.
Con la aclaratoria anterior, aplicamos raíz cuadrada en ambos lados.
\sqrt{{m}^{2}}>\sqrt{mn}\to m>\sqrt{mn}
Que es equivalente a decir:
\sqrt{mn}<m
Concluimos finalmente que: Si m>n , el resultado de \sqrt{mn} es menor que m. Comparando con las opciones, la respuesta correcta es la C.
Reactivo 103: Logaritmos
El logaritmo base 10 de 10 es igual a:
- 10
- 1
- 100
- .01
- 10.10
Solución:
Por propiedad de los logaritmos, el logaritmo base a de a es igual a 1.
a =x\to {a}^{x}=a
¿Qué valor debe tener x para que al elevar a a dicho número el resultado sea a ?, en efecto 1. Concluimos que:
El logaritmo base 10 de 10 es igual a 1.
Seleccionamos como respuesta correcta a la opción B.
Reactivo 104: Propiedades de las potencias
Al simplificar \frac{{7}^{4}}{{7}^{3}}\left({7}^{2}\right) , obtenemos:
- {7}^{\frac{4}{3}}
- {7}^{\frac{3}{4}}
- 7
- {7}^{3}
- 1
Solución:
En este caso, se deben aplicar las propiedades del producto de potencias de igual base y el cociente de potencias de igual base. Comencemos por aplicar el cociente de potencias; conservamos la misma base y se restan los exponentes.
\frac{{7}^{4}}{{7}^{3}}\left({7}^{2}\right)={7}^{4-3}*{7}^{2}=7*{7}^{2}
Ahora, el producto de potencias de igual base.
7*{7}^{2}={7}^{1+2}={7}^{3}
Comparando con las opciones, escogemos como respuesta correcta a la D.
Reactivo 105: Técnicas de conteo
¿De cuántas formas diferentes se pueden acomodar ocho personas en 8 sillas?
- 4!
- 8
- 64
- 8!
- 7!
Solución:
Para resolver cualquier problema de conteo, podemos utilizar variaciones, permutaciones o combinaciones. Decidir cuál escoger depende de si importa o no el orden de los objetos.
Imaginemos que tenemos los números 1, 2, 3, ¿es igual 123 qué 321? Por supuesto que no; entonces sí importa el orden y debemos recurrir a variaciones o permutaciones.
En este caso, ¿importa el lugar que ocupe cada una de las 8 personas en las 8 sillas?, sí. No será igual, por ejemplo, mujeres a la izquierda y hombres a la derecha que un hombre y una mujer de forma intercalada.
Ahora, ¿es una variación o una permutación? Se usan variaciones si empleamos a todos los elementos y permutaciones si es solo una parte de ellos. Son 8 personas y 8 asientos ¡es una variación!
V=n!
Si n=8 entonces:
V=8!
Comparando con las opciones del problema, seleccionamos como correcta a la D.
Reactivo 106: Operaciones con fracciones
¿Cuál es el número qué es las \frac{2}{3} partes de \frac{1}{2} del doble de 6?
- 4
- 5
- 10
- 6
- 2
Solución:
Debemos calcular el valor de un número cualquiera x , que es igual a la relación entre números fracciones, indicada por el enunciado.
En este tipo de problemas, debemos resolver desde el final hacia el inicio. Comenzamos con doble de 6:
2*6=12
Ahora, vamos con \frac{1}{2} del doble:
\frac{1}{2}*12=6
Finalmente, con las \frac{2}{3} partes de:
\frac{2}{3}*6=4
De esta forma, dicho número x es igual a 4.
Comparando con las opciones, seleccionamos como correcta a la A.
Reactivo 107: Igualdades numéricas
¿Por qué número se tiene que dividir 80 para que el resultado sea \frac{3}{5} ?
- 123\frac{1}{2}
- 130
- 129
- 133\frac{1}{3}
- 143
Solución:
En este caso, debemos calcular un número x tal que, al dividirse entre 80 \frac{80}{x} sea igual a la fracción \frac{3}{5} . Lo anterior se puede expresar mediante la siguiente igualdad:
\frac{80}{x}=\frac{3}{5}
Simplificamos.
x=\frac{80}{\frac{3}{5}}
Aplicamos la regla de la doble tortilla o doble c.
x=\frac{5*80}{3}=\frac{400}{3}
Ya que algunas de las opciones están expresadas en fracción mixta, debemos convertir nuestro resultado a esa forma. Realizamos el cociente entre el numerador y el denominador, quedando:
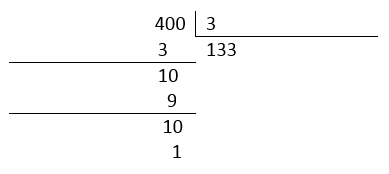
Finalmente:
x=\frac{400}{3}=133\frac{1}{3}
Comparando con las opciones, la respuesta correcta sería la D.
Reactivo 108: Interés
El Señor Gutiérrez recibe el 7% anual por concepto de interés sobre una inversión que efectuó. Si al final del año sus intereses son $350, ¿Cuánto invirtió inicialmente?
- $500
- $600
- $2450
- $5000
- $50000
Solución:
Ya que no se está indicando alguna acumulación del interés, podemos asegurar que el modelo de inversión que siguió el Señor Gutiérrez es de tipo interés simple. La fórmula para calcular el interés simple es:
I=P*i*n
Donde:
- P es el capital
- i es el porcentaje de interés anual
- n son los años
- I es el interés simple
Despejamos de la fórmula el capital P .
P=\frac{I}{i*n}
Sustituimos.
P=\frac{\$350}{0.07*1}=\$5000
La inversión inicial del Señor Gutiérrez fue de cinco mil pesos. Comparando con las opciones, la respuesta correcta es la D.
Reactivo 109: Fracciones y lenguaje natural
La mitad de un tercio es igual a:
- Un sexto
- Dos tercios
- Un quinto
- Uno
- Tres medios
Solución:
En este caso, debemos identificar las cantidades en juego y la operación que se realiza entre ellas. La primera parte de la frase: la mitad de… nos indica que el número que se menciona a continuación de los tres puntos va a ser dividido entre dos, esa cantidad es \frac{1}{3} .
La frase expresa que un tercio \frac{1}{3} se divide entre 2.
\frac{\frac{1}{3}}{2}
Aplicamos la regla de la doble tortilla:
\frac{\frac{1}{3}}{\frac{2}{1}}=\frac{1*1}{2*3}=\frac{1}{6}
Concluimos que:
La mitad de un tercio es igual a un sexto.
Concluimos el problema seleccionando como respuesta correcta a la opción A.
Reactivo 110: Triángulo rectángulo
En el siguiente triángulo rectángulo, señala cuál de las expresiones siguientes corresponde a la longitud de la hipotenusa.
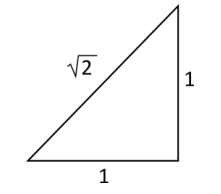
- h=2
- h=\sqrt{5}
- h=\sqrt{2}
- h=\sqrt{3}
- h=\sqrt{1}
Solución:
Tenemos dos formas de identificar cual es la hipotenusa en el triángulo de la imagen. Una es a través del Teorema de Pitágoras y la otra es de forma gráfica.
Aplicando el teorema de Pitágoras, se debe comprobar que la suma de los cuadrados de dos lados sea igual al cuadrado del otro, será entonces este último la hipotenusa.
Viendo cuánto mide cada lado, es fácil pensar en la siguiente igualdad:
{\left(\sqrt{2}\right)}^{2}={1}^{2}+{1}^{2}
Se elimina la raíz con el cuadrado y nos queda:
2=2
Concluimos entonces que la hipotenusa es \sqrt{2} .
h=\sqrt{2}
Seleccionamos como respuesta correcta a la opción C.

