Guía UAM CSH: Ciencias sociales y humanidades | Matemáticas parte 1

¡Hola de nuevo aspirante! En este post vamos a resolver la primera parte de la guía de ingreso CSH sobre Matemáticas para el examen de ingreso a la UAM. Específicamente, desarrollaremos los ejercicios del 90 al 99.

Parte II

La siguiente lista, contiene un resumen de la convocatoria a la UAM 2022.

Estructura del examen de ingreso UAM 2022

La prueba se encuentra dividida en dos partes: una de aptitud y otra de conocimientos específicos, que varía en función a la división de tu carrera.

La primera parte cubre los temas de razonamiento matemático y razonamiento verbal. Posee una extensión total de 40 problemas y tiene la particularidad de permanecer constante para las 6 divisiones.

Por otro lado, la segunda parte para Ciencias Sociales y Humanidades, tiene las siguientes asignaturas: literatura, historia, formación cívica y política, filosofía y matemáticas..

El siguiente, es un resumen de la parte de conocimientos específicos para CSH.

Literatura

• El lenguaje literario.
• Los géneros literarios.
• Principales autores literarios hispanos y latinoamericanos.

Historia de México

• Mesoamérica.
• Independencia.
• La República Liberal.
• La República Restaurada.
• El Porfiriato.
• La Revolución.
• México posrevolucionario.

Historia universal

• Civilizaciones antiguas: Grecia y Roma.
• Feudalismo.
• Renacimiento.
• Expansión europea.
• Revolución industrial y revoluciones burguesas.
• Antecedentes y consecuencias de las conflagraciones mundiales del Siglo XX.
• Descolonización y democratización.

Formación cívica y política

• Organización política.
• Sistema político mexicano.
• Organización social.

Filosofía

• Principales problemas filosóficos.
• La evolución de las cuestiones y perspectivas filosóficas.
• Lógica.

Matemáticas.

• Aritmética.
• Álgebra.
• Geometría Plana.
• Geometría Analítica.

Resumen de reactivos en cada parte del examen.

Área	Reactivos	Porcentaje
Razonamiento verbal	20	25%
Razonamiento matemático	20	25%
Conocimientos específicos	40	50%
Total	80	100%

Temario de Matemáticas para CSH

Estos son los temas que debes trabajar en el área de matemáticas de la prueba de conocimientos específicos para la división CSH.

Aritmética

• Operaciones con fracciones (suma, resta, multiplicación, división) y simplificaciones.
• Razones y proporciones.
• Descomposición de números en factores primos.

Álgebra

• Números reales.
• Manejo de exponentes y radicales.
• Operaciones con polinomios.
• Factorización.
• Operaciones y simplificación de expresiones racionales.
• Resolución de ecuaciones de primer y segundo grado.

Geometría plana

• Perpendicularidad. Construcciones simétricas.
• Paralelismo, semejanza de figuras geométricas.
• Criterios de semejanza de triángulos.
• Ángulos entre paralelas.
• Teorema de Tales y teorema de Pitágoras.

Geometría analítica

• Sistema de coordenadas.
• La noción de lugar geométrico.
• Ecuación lineal: tabulación y graficación.

Guía UAM CSH Matemáticas parte 1

Finalizada esta introducción, solo nos queda pasar a la solución de los reactivos. Un aspecto que muchos estudiantes pasan por alto es el tiempo que tardan al resolver los reactivos.

Reactivo 90: Ordenamiento de números reales

Dados los números \sqrt{2},\frac{2}{13},\frac{1}{4},\frac{5}{3},\frac{9}{8} el de mayor valor es:

1. \frac{5}{3}
2. \frac{2}{13}
3. \frac{1}{4}
4. \frac{9}{8}
5. \sqrt{2}

Solución:

Ya que tenemos una mezcla de números fraccionarios con radicales, debemos:

1. Hacer que todos tengan el mismo denominador (hay que calcular el mcm)
2. Expresarlos a todos como radicales

Comenzamos por calcular el mcm de los denominadores de todos los números.

mcm\left(\mathrm{1,13,4},\mathrm{3,8}\right)=312

Multiplicamos y dividimos cada fracción por un número tal que en el denominador de como resultado 312.

Fracción 1.

\frac{312\sqrt{2}}{312}

Fracción 2.

x=\frac{312}{13}=24\to \frac{2}{13}*\frac{24}{24}

\frac{48}{312}

Fracción 3.

x=\frac{312}{4}=78\to \frac{1}{4}*\frac{78}{78}

\frac{78}{312}

Fracción 4.

x=\frac{312}{3}=104\to \frac{5}{3}*\frac{104}{104}

\frac{520}{312}

Fracción 5.

x=\frac{312}{8}=39\to \frac{9}{8}*\frac{39}{39}

\frac{351}{312}

Las fracciones serían:

\frac{312\sqrt{2}}{312},\frac{48}{312}, \frac{78}{312}, \frac{520}{312}, \frac{351}{312}

Ahora, a cada número lo elevamos al cuadrado y le aplicamos raíz cuadrada. A los del numerador como a los del denominador exceptuando \sqrt{2} porque ya tiene raíz.

\frac{\sqrt{{312}^{2}}\sqrt{2}}{\sqrt{{312}^{2}}},\frac{\sqrt{{48}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{78}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{351}^{2}}}{\sqrt{{312}^{2}}}

En la primera fracción aplicamos la propiedad del producto de raíces de igual índice.

\frac{\sqrt{{312}^{2}*2}}{\sqrt{{312}^{2}}},\frac{\sqrt{{48}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{78}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{351}^{2}}}{\sqrt{{312}^{2}}}

Con los números escritos de esta forma, podemos seleccionar cual es el mayor verificando el que tenga en el numerador el radicando mayor. Podemos descartar a {48}^{2} y {78}^{2} porque son significativamente menores al resto.

Como {351}^{2} y {312}^{2} son números muy cercanos, podemos descartar a {351}^{2} porque {312}^{2} está multiplicado por dos. Solo quedan {520}^{2} y {312}^{2}*2 , podemos incluir el 2 dentro de la potencia si lo expresamos como:

{312}^{2}*{\sqrt{2}}^{2}={\left(312*\sqrt{2}\right)}^{2}

Ahora, \sqrt{2} es aproximadamente 1.414.

{\left(312*\sqrt{2}\right)}^{2}\approx {\left(312*1.414\right)}^{2}

Este producto es más sencillo de realizar y es igual a:

{\left(312*1.414\right)}^{2}={441.168}^{2}

La potencia {441.168}^{2} es menor que {520}^{2} , por tanto concluimos que el número mayor es:

\frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}=\frac{520}{312}=\frac{5}{3}

Concluimos entonces que la respuesta correcta es la opción A.

Reactivo 91: Porcentajes

¿De qué número es 196 el 0.56%?

1. 100000
2. 35000
3. 128000
4. 19600
5. 40000

Solución:

Para resolver este problema, emplearemos la fórmula para calcular el porcentaje de una cantidad respecto de otra.

N=\frac{\%*{N}_{r}}{100\%}

Donde N es el resultado del porcentaje y {N}_{r} es la cantidad de referencia o a la que le queremos calcular el porcentaje. En nuestro caso 196 es el resultado obtenido, es decir N y lo que nos piden es a {N}_{r} . Debemos despejar a {N}_{r} de la fórmula.

N=\frac{\%*{N}_{r}}{100\%}\to {N}_{r}=\frac{100\%*N}{\%}

Sustituimos los valores dados.

{N}_{r}=\frac{100\%*\left(196\right)}{0.56\%}=\mathrm{35,000}

Finalmente, el número del que 196 es el 0.56% es 35000.

Concluimos seleccionando como correcta a la opción B.

Reactivo 92: Valor numérico de una expresión

Calcula el valor numérico de la expresión \frac{3{m}^{2}}{\sqrt{2n}} con m=3 , n=2

1. \frac{27}{2}
2. \frac{9}{4}
3. \frac{27}{4}
4. \frac{9}{2}
5. \frac{12}{2}

Solución:

Para encontrar el valor numérico de la expresión, debemos sustituir en la misma los valores dados de m y n , resolver las operaciones indicadas y simplificar la fracción de ser posible.

Sustituyendo valores.

\frac{3{m}^{2}}{\sqrt{2n}}\to \frac{3{\left(3\right)}^{2}}{\sqrt{2\left(2\right)}}

Resolvemos las operaciones.

\frac{3{\left(3\right)}^{2}}{\sqrt{2\left(2\right)}}=\frac{3*9}{\sqrt{4}}=\frac{27}{2}

La fracción no puede simplificarse porque tanto el numerador como el denominador son primos.

Concluimos indicando que la respuesta correcta es la opción A.

Reactivo 93: Operaciones con signos

Al eliminar los paréntesis en la expresión -(a+b)+(2a-b)-(2a-b) , el resultado es:

1. -a+b
2. a-2b
3. -a-b
4. a-b
5. -a+2b

Solución:

Para encontrar la expresión simplificada, debemos seguir el siguiente orden:

• Resolver las operaciones dentro de los paréntesis (si se puede)
• Realizar distributiva con el signo delante de los paréntesis hacia su interior, aplicando las propiedades de los signos

En un principio, dentro de los paréntesis de cada término no hay elementos semejantes, por tanto, pasamos directamente a aplicar distributiva del signo.

-\left(a+b\right)+\left(2a-b\right)-\left(2a-b\right)=-a-b+2a-b-2a+b

Agrupamos términos semejantes.

=-a-b+2a-b-2a+b=-a+2a-2a-b-b+b

Resolvemos las sumas y restas.

=-a+2a-2a-b-b+b=-a-b

El resultado de eliminar los paréntesis es:

-\left(a+b\right)+\left(2a-b\right)-\left(2a-b\right)=-a-b

Comparando con las opciones, encontramos que la respuesta correcta es la C.

Reactivo 94: Operaciones con números enteros

El resultado de la operación -[-(-16)+10] es:

1. 26
2. 16
3. 10
4. -26
5. -16

Solución:

Seguimos la regla para deshacer paréntesis y corchetes:

• Resolver las operaciones dentro de los corchetes
• Resolver las operaciones dentro de los paréntesis
• Resolver el resto

En este caso, dentro de los corchetes hay un término con paréntesis, por tanto iniciamos con él. Como no hay  más que un -16 dentro de los paréntesis, los deshacemos aplicando distributiva con el signo menos:

-\left[-\left(-16\right)+10\right]=-[16+10]

Resolvemos la suma dentro de los corchetes.

-\left[16+10\right]=-\left[26\right]

Deshacemos los corchetes multiplicando el menos por el número de adentro.

-\left[26\right]=-26

Comparando con las opciones, la respuesta correcta es la opción D.

Reactivo 95: Suma de fracciones

La operación \frac{x}{1-x}+\frac{3}{2x+3} es igual a:

1. \frac{x+3}{x+4}
2. x+\frac{3}{2x}
3. \frac{{x}^{2}+1}{1+{x}^{2}}
4. \frac{x+3}{3-x-2{x}^{2}}
5. \frac{2{x}^{2}+3}{3-x-2{x}^{2}}

Solución:

Debemos aplicar la regla del producto cruzado para la suma de fracciones:

\frac{a}{b}+\frac{c}{d}=\frac{a*d+c*b}{b*d}

Producto cruzado:

\frac{x}{1-x}+\frac{3}{2x+3}=\frac{x\left(2x+3\right)+3\left(1-x\right)}{\left(1-x\right)\left(2x+3\right)}

Desarrollamos los productos.

\frac{x\left(2x+3\right)+3\left(1-x\right)}{\left(1-x\right)\left(2x+3\right)}=\frac{2{x}^{2}+3x+3-3x}{2x\left(1-x\right)+3\left(1-x\right)}=\frac{2{x}^{2}+3x+3-3x}{2x-2{x}^{2}+3-3x}

Simplificamos sumas y restas de términos semejantes.

\frac{2{x}^{2}+3x+3-3x}{2x-2{x}^{2}+3-3x}=\frac{2{x}^{2}+3}{-2{x}^{2}-x+3}=\frac{2{x}^{2}+3}{3-x-2{x}^{2}}

El resultado de sumar \frac{x}{1-x}+\frac{3}{2x+3} es:

\frac{x}{1-x}+\frac{3}{2x+3}=\frac{2{x}^{2}+3}{3-x-2{x}^{2}}

Comparando con las opciones del problema, la respuesta correcta es la E.

Reactivo 96: Ecuación de segundo grado

Las dos soluciones de la ecuación \sqrt{4{x}^{2}-12x+9}=3 son:

1. x=0;x=4
2. x=0;x=3
3. x=1;x=4
4. x=0;x=-3
5. x=1;x=3

Solución:

Es claro que la fórmula resultante será de segundo grado, pero antes hay que deshacernos de la raíz cuadrada. Elevamos al cuadrado ambos lados:

{\left(\sqrt{4{x}^{2}-12x+9}\right)}^{2}={3}^{2}\to 4{x}^{2}-12x+9=9

Simplificamos.

4{x}^{2}-12x=0

{x}^{2}-3x=0

En este caso tenemos dos opciones: aplicar fórmula de segundo grado donde el término c=0 o factorizar. Por ser la opción más rápida, vamos a factorizar extrayendo factor común la x .

{x}^{2}-3x=0\to x\left(x-3\right)=0

Despejamos los valores que debe tener x para que la expresión sea igual a cero:

x=0

x-3=0\to x=3

Concluimos que las dos soluciones de la ecuación \sqrt{4{x}^{2}-12x+9}=3 son x=0 y x=3 .

Comparando con las opciones, seleccionamos como respuesta correcta la B.

Reactivo 97: Simplificación de expresiones algebraicas

Si x\ne y , entonces la expresión \frac{{x}^{3}-{y}^{3}}{x-y}-{y}^{2} es igual a:

1. {y}^{2}-xy
2. xy-{x}^{2}
3. {x}^{2}+xy
4. {x}^{2}-xy
5. x+xy

Solución:

Para encontrar la forma más simplificada de la expresión dada, debemos efectuar la resta de los términos y desarrollar las operaciones correspondientes. Recordemos que todo número puede expresarse como una fracción con denominador igual a 1.

\frac{{x}^{3}-{y}^{3}}{x-y}-{y}^{2}=\frac{{x}^{3}-{y}^{3}}{x-y}-\frac{{y}^{2}}{1}

Producto cruzado para la resta de fracciones.

\frac{{x}^{3}-{y}^{3}}{x-y}-\frac{{y}^{2}}{1}=\frac{{x}^{3}-{y}^{3}-{y}^{2}\left(x-y\right)}{x-y}

Desarrollamos.

\frac{{x}^{3}-{y}^{3}-{y}^{2}\left(x-y\right)}{x-y}=\frac{{x}^{3}-{y}^{3}-{y}^{2}x+{y}^{3}}{x-y}

Agrupamos términos semejantes.

\frac{{x}^{3}-{y}^{3}-{y}^{2}x+{y}^{3}}{x-y}=\frac{{x}^{3}-{y}^{3}+{y}^{3}-{y}^{2}x}{x-y}=\frac{{x}^{3}-{y}^{2}x}{x-y}

Extraemos factor común x .

\frac{{x}^{3}-{y}^{2}x}{x-y}=\frac{x\left({x}^{2}-{y}^{2}\right)}{x-y}

Aplicamos diferencia de cuadrados en el binomio del numerador.

\frac{x\left({x}^{2}-{y}^{2}\right)}{x-y}=\frac{x\left(x-y\right)\left(x+y\right)}{x-y}

Simplificamos x-y en el numerador y denominador.

\frac{x\left(x-y\right)\left(x+y\right)}{x-y}=x\left(x+y\right)

Por último, aplicamos distributiva.

x\left(x+y\right)={x}^{2}+xy

Concluimos finalmente que:

\frac{{x}^{3}-{y}^{3}}{x-y}-{y}^{2}={x}^{2}-xy

Comparando con las opciones, seleccionamos como correcta a la C.

Reactivo 98: Sistema de ecuaciones

La solución del sistema de ecuaciones \left\{\begin{array}{c}{x}^{2}-1=3\\ x+y=4\end{array}\right. es:

1. \left(-\mathrm{2,2}\right);\left(-\mathrm{2,6}\right)
2. \left(2,-2\right);\left(-\mathrm{2,6}\right)
3. \left(\mathrm{2,2}\right);\left(-2,-6\right)
4. \left(\mathrm{2,2}\right);\left(-\mathrm{2,6}\right)
5. \left(\mathrm{2,2}\right);\left(2,-6\right)

Solución:

Para resolver el sistema de ecuaciones, debemos identificar el método más conveniente que nos permita encontrar los valores de x y y . El sistema está compuesto por una ecuación de segundo grado (que no es una parábola porque no está la variable y ) y una recta.

En la primera ecuación sólo está presente la variable x , por tal razón, podríamos despejar de ella a x y luego sustituir en la segunda para hallar a y .

Despejando a x .

{x}^{2}-1=3\to {x}^{2}=4

x=\pm 2

Tenemos dos valores de x :

{x}_{1}=2 y {x}_{2}=-2

Sustituimos ahora ambos valores en la segunda ecuación para obtener la coordenada en y de cada punto.

x+y=4\to y=4-x

Para {x}_{1}=2 :

{y}_{1}=4-2=2

Para {x}_{2}=-2 :

{y}_{2}=4-\left(-2\right)=6

Los puntos de corte entre la recta y la ecuación cuadrática son:

{P}_{1}\left(\mathrm{2,2}\right) y {P}_{2}\left(-\mathrm{2,6}\right)

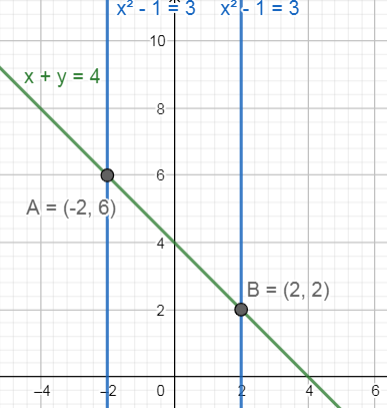
Comparando con las opciones, seleccionamos como respuesta correcta a la D.

Reactivo 99: Completación de cuadrados

La expresión {x}^{2}-5x+\frac{33}{4} es igual a:

1. {\left(x+\frac{5}{2}\right)}^{2}+2
2. {\left(x-\frac{5}{2}\right)}^{2}-2
3. {\left(x-\frac{5}{2}\right)}^{2}+2
4. {\left(x+\frac{5}{2}\right)}^{2}-2
5. (x-5{)}^{2}+2

Solución:

Para aplicar completación de cuadrados, tenemos que hacer que convertir el polinomio a un trinomio cuadrado perfecto:

{\left(x-b\right)}^{2}={x}^{2}-2bx+{b}^{2}

En este caso, el factor del término cuadrático del polinomio dado es igual al trinomio modelo, es decir 1. Por otro lado, el factor del término de primer grado 5 debe ser igual a b multiplicado por dos:

5=2b

Despejamos de acá a b :

b=\frac{5}{2}

Al polinomio podemos escribir entonces como:

{x}^{2}-2*\frac{5}{2}x+\frac{33}{4}

El término independiente debe ser igual a {b}^{2} . Como b=\frac{5}{2} su cuadrado es igual a \frac{25}{4} pero en nuestro caso es \frac{33}{4} , haremos el truco de sumar y restar \frac{25}{4} de esta forma no alteramos la igualdad.

{x}^{2}-2*\frac{5}{2}x+\frac{25}{4}-\frac{25}{4}+\frac{33}{4}

Ahora, aplicamos {\left(x-b\right)}^{2}={x}^{2}-2bx+{b}^{2} pero en sentido inverso con los 3 primeros términos del polinomio {x}^{2}-2*\frac{5}{2}x+\frac{25}{4} .

{\left(x-\frac{5}{2}\right)}^{2}-\frac{25}{4}+\frac{33}{4}

Por último, simplificamos la resta.

{\left(x-\frac{5}{2}\right)}^{2}+\frac{8}{4}={\left(x-\frac{5}{2}\right)}^{2}+2

Finalmente, podemos afirmar que:

La expresión {x}^{2}-5x+\frac{33}{4} es igual a {\left(x-\frac{5}{2}\right)}^{2}+2 .

Comparando con las opciones, la respuesta correcta es la C.