¡Ya casi acabamos aspirante! Vamos con los reactivos del 63 al 72, que corresponden a la sexta parte de la guía de ingreso resuelta para las divisiones de CBI y CNI del examen a la Universidad Autónoma Metropolitana.

Guía UAM Matemáticas Parte 6 resuelta
Vamos con la solución paso a paso de la sexta y penúltima parte de esta guía de matemáticas para el examen de ingreso a la UAM.
Para el 2022, la prueba cambió de modalidad presencial a modalidad en línea, asegúrate de tomar todas las previsiones y toma el examen de prueba para comprobar tu equipo y conexión a internet.
Reactivo 63: Ecuación de segundo grado
Las soluciones de la ecuación {x}^{2}-10ax+9{a}^{2}=0 son _______.
- {x}_{1}=a,{x}_{2}=a
- {x}_{1}=a,{x}_{2}=9a
- {x}_{1}=3a,{x}_{2}=0
- {x}_{1}=4.5a,{x}_{2}=3a
- {x}_{1}=3a,{x}_{2}=5a
Solución:
Tenemos dos caminos para calcular las raíces del polinomio de segundo grado: la fórmula cuadrática o mediante factorización. Por ser la vía más rápida, optamos esta vez por la fórmula cuadrática.
{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
En este caso:
a=1
b=-10a
c=9{a}^{2}
Sustituimos:
{x}_{\mathrm{1,2}}=\frac{-\left(-10a\right)\pm \sqrt{{\left(-10a\right)}^{2}-4\left(1\right)\left(9{a}^{2}\right)}}{2}=\frac{10a\pm \sqrt{100{a}^{2}-36{a}^{2}}}{2}
{x}_{\mathrm{1,2}}=\frac{10a\pm \sqrt{64{a}^{2}}}{2}=\frac{10a\pm 8a}{2}
{x}_{1}=\frac{10a-8a}{2}=a
{x}_{2}=\frac{10a+8a}{2}=9a
Finalmente:
Las soluciones de la ecuación {x}^{2}-10ax+9{a}^{2}=0 son {x}_{1}=a, {x}_{2}=9a .
Comparando con las opciones, escogemos como correcta a la B.
Reactivo 64: Solución de ecuaciones
La solución de la ecuación \frac{4}{x-2}-\frac{4}{3x-6}=-\frac{8}{3} es _____________.
- 0
- 2
- -2
- -1
- 1
Solución:
Comenzamos por eliminar los monomios de los denominadores en las fracciones, para ello multiplicamos ambos miembros de la ecuación por x-2 y luego por 3x-6 .
Multiplicando por x-2 .
\left(\frac{4}{x-2}-\frac{4}{3x-6}\right)\left(x-2\right)=-\frac{8}{3}\left(x-2\right)
4-4\frac{x-2}{3x-6}=-\frac{8}{3}\left(x-2\right)
Multiplicando por 3x-6 .
\left(4-4\frac{x-2}{3x-6}\right)\left(3x-6\right)=-\frac{8}{3}\left(3x-6\right)\left(x-2\right)
4\left(3x-6\right)-4\left(x-2\right)=-\frac{8}{3}\left(3x-6\right)\left(x-2\right)
Dividimos ambos miembros por 4 y luego multiplicamos por 3.
3x-6-\left(x-2\right)=-\frac{2}{3}\left(3x-6\right)\left(x-2\right)
3\left(3x-6\right)-3\left(x-2\right)=-2\left(3x-6\right)\left(x-2\right)
Desarrollamos los productos.
9x-18-3x+6=-2\left(3x-6\right)\left(x-2\right)
6x-12=-2\left(3x-6\right)\left(x-2\right)
Extraemos el factor común del primer miembro 2.
2\left(3x-6\right)=-2\left(3x-6\right)\left(x-2\right)
Dividimos ambos miembros por 3x-6 .
2=-2\left(x-2\right)
Dividimos por -2.
-1=x-2
Despejamos x .
x=2-1
\therefore x=1
Finalmente:
La solución de la ecuación \frac{4}{x-2}-\frac{4}{3x-6}=-\frac{8}{3} es 1.
Comparando con las opciones, seleccionamos como respuesta correcta a la opción E.
Reactivo 65: Área de la base de un cilindro
Un tanque cilíndrico tiene una altura igual al doble de su radio. Si el volumen del tanque es V=16 {m}^{3} ¿Cuánto mide su área lateral?
- 16\sqrt[3]{{\pi }^{2}}
- 8\sqrt[3]{{\pi }^{2}}
- 8\pi
- 4\sqrt[3]{\pi }
- 16\sqrt[3]{\pi }
Solución:
En este caso, el área que solicita el ejercicio es la sección transversal del tanque.
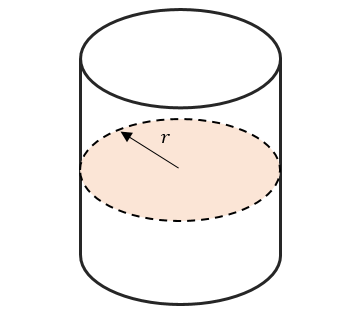
La ecuación del volumen de un cilindro es:
{V}_{c}=\pi {r}^{2}h\to 16 {cm}^{3}=\pi {r}^{2}h
Donde r es el radio y h la altura del cilindro. Por otro lado el enunciado nos dice que la altura es igual al doble del radio, es decir:
h=2r
Sustituimos en la ecuación del volumen.
16 {cm}^{3}=\pi {r}^{2}\left(2r\right)\to 16 {cm}^{3}=2\pi {r}^{3}
Despejamos el radio.
r=\sqrt[3]{\frac{16}{2\pi }}
Sustituimos en la ecuación del área de un círculo.
A=\pi {r}^{2}\to A=\pi {\left(\frac{16}{2\pi }\right)}^{\frac{2}{3}}
Simplificamos la expresión.
A=\pi {\left(\frac{16}{2\pi }\right)}^{\frac{2}{3}}=\pi {\left(\frac{8}{\pi }\right)}^{\frac{2}{3}}=\frac{\pi }{{\pi }^{\frac{2}{3}}}{\left(\sqrt[3]{8}\right)}^{2}
=\frac{\pi }{{\pi }^{\frac{2}{3}}}{\left(\sqrt[3]{8}\right)}^{2}={\pi }^{1-\frac{2}{3}}{\left(2\right)}^{2}={\pi }^{\frac{1}{3}}\left(4\right)
\therefore A=4\sqrt[3]{\pi } {cm}^{2}
Concluimos escogiendo como respuesta correcta a la opción D.
Reactivo 66: Relación entre ángulos
En el siguiente diagrama ¿Cuál es el valor en grados del ángulo z?
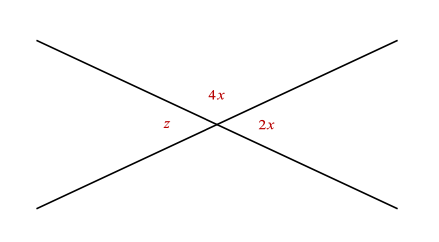
- 30°
- 100°
- 60°
- 80°
- 40°
Solución:
Para encontrar el valor de z , debemos relacionar los ángulos mediante ángulos opuestos por el vértice y ángulos suplementarios.
Son opuestos por el vértice z y 2x , por tanto:
z=2x \left(I\right)
Son suplementarios 4x y 2x , como también z y 4x .
4x+2x=180 \left(II\right)
z+4x=180 \left(III\right)
En este caso, las ecuaciones II y III son iguales, ya que si se sustituye I en III se obtiene a II. Nos conviene utilizar la ecuación II para despejar a x y luego sustituir su valor en z .
4x+2x=180\to 6x=180\to x=30
Sustituyendo en \left(I\right) .
z=2\left(30\right)=60
Concluimos indicando que z vale 60°.
Comparando con las opciones, seleccionamos a C como la correcta.
Reactivo 67: Teorema de Tales
Un joven mide 6 pies de altura y su sombra mide 4 pies de longitud; si la sombra de un árbol mide 24 pies de largo ¿Qué altura tiene el árbol?
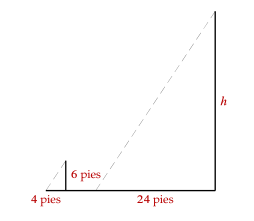
- 30 pies
- 26 pies
- 36 pies
- 24 pies
- 28 pies
Solución:
Para calcular la altura del árbol, debemos recurrir al teorema de Tales o de triángulos semejantes. Específicamente, el criterio de proporcionalidad de lados; donde el cociente entre la altura del joven y la altura del árbol es igual al cociente de las sombras.
Si {s}_{j} y {s}_{a} son las sombras del joven y el árbol, y {h}_{j} y {h}_{a} las alturas respectivamente, el criterio de proporcionalidad de lados queda como:
\frac{{s}_{j}}{{s}_{a}}=\frac{{h}_{j}}{{h}_{a}}
Despejamos la altura del árbol.
{h}_{a}=\frac{{h}_{j}}{{s}_{j}}*{s}_{a}
Sustituimos.
{h}_{a}=\frac{6}{4}*24=36 pies
El árbol tiene una altura de 36 pies.
Concluimos seleccionando como respuesta correcta a la opción C.
Reactivo 68: Identidades trigonométricas
Del siguiente triángulo rectángulo, la identidad trigonométrica falsa es ________.
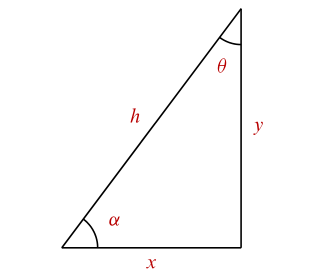
- cot \alpha =\frac{x}{y}
- sec \theta =\frac{y}{h}
- csc \alpha =\frac{h}{y}
- tan \theta =\frac{x}{y}
- csc \theta =\frac{h}{x}
Solución:
En este caso, examinaremos cada identidad trigonométrica para comprobar que sea correcta; de no serlo concluimos con la solución y la seleccionamos como falsa.
Cotangente de alfa.
La cotangente es la función inversa de la tangente. Respecto a alfa representa el cociente entre el cateto adyacente sobre el cateto opuesto.
cot \alpha =\frac{CA}{CO}
x es adyacente a alfa y y es el opuesto, por tanto:
cot \alpha =\frac{CA}{CO}=\frac{x}{y}
No es la identidad falsa.
Secante de teta.
La secante es la función inversa del coseno. Respecto al ángulo teta representa el cociente entre la hipotenusa y el cateto adyacente.
sec \theta =\frac{H}{CA}
h es la hipotenusa y y es el cateto adyacente, por tanto:
sec \theta =\frac{H}{CA}=\frac{h}{y}
El inciso muestra la relación al revés. Esta es la identidad falsa.
Del siguiente triángulo rectángulo, la identidad trigonométrica falsa es sec \theta =\frac{y}{h} .
Seleccionamos a la B como la respuesta correcta.
Reactivo 69: Perímetro de una circunferencia
La figura muestra un círculo de área igual a 25\pi , dividido en 8 partes iguales ¿Cuál es el perímetro de la región sombreada?
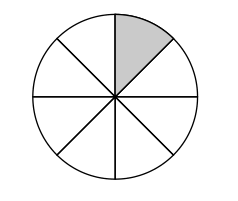
- 5\left(3+\frac{\pi }{4}\right)
- 5\left(1+\frac{\pi }{4}\right)
- 5\left(2+\frac{\pi }{4}\right)
- 5\left(2+\frac{\pi }{8}\right)
- 5\left(1+\frac{\pi }{8}\right)
Solución:
El perímetro de la sección sombreada es la suma de los dos lados rectos (que son iguales al radio) y la sección curva:
{P}_{tc}=2r+{P}_{p}
Ya que cada una de las 8 partes son iguales, tanto el perímetro como el área es una octava parte del total, es decir:
{A}_{p}=\frac{{A}_{c}}{8}
{P}_{p}=\frac{{P}_{c}}{8}
El área y el perímetro del círculo se calculan como:
{A}_{c}=\pi {r}^{2}
{P}_{c}=2\pi r
De la ecuación de área, podemos despejar el valor del radio para sustituirlo en la ecuación del perímetro.
{A}_{c}=\pi {r}^{2}\to r=\sqrt{\frac{{A}_{c}}{\pi }}
\therefore r=\sqrt{\frac{25\pi }{\pi }}=\sqrt{25}=5
{P}_{c}=\frac{2\pi \left(5\right)}{8}=\frac{10\pi }{8}=\frac{5\pi }{4}
Calculamos el perímetro de la sección sombreada.
{P}_{tc}=2r+{P}_{p}\to {P}_{tc}=2\left(5\right)+\frac{5\pi }{4}=5\left(2+\frac{\pi }{4}\right)
Se concluye el ejercicio escogiendo como correcta a la opción C.
Reactivo 70: Trigonometría
En el siguiente triángulo isósceles, determine el valor del ángulo A en radianes.
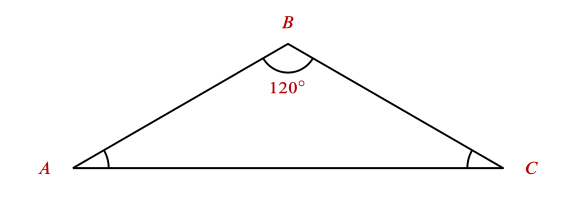
- \frac{\pi }{12}rad
- \pi rad
- \frac{\pi }{6}rad
- 30\pi rad
- \frac{\pi }{3}rad
Solución:
Un triángulo isósceles es aquel con 2 lados y 2 ángulos iguales. En la situación planteada en la imagen, son iguales los lados BA y BC , por tanto son iguales los ángulos \widehat{A} y \widehat{C} . Ya que la suma de ángulos en un triángulo el siempre 180°, decimos que:
180°=120°+2A
2A=60°\to A=30°
Ahora debemos transformar el resultado a radianes. Utilizamos la relación que dice:
180°\to \pi
30°\to x
x=\frac{30°*\pi }{180°}=\frac{\pi }{6}rad
Concluimos el reactivo seleccionando como respuesta correcta a la opción C.
Reactivo 71: Ecuación de la circunferencia
Determinar la ecuación de la circunferencia si A(-\mathrm{2,3}) y B(4,-5) son los extremos de uno de sus diámetros.
- {x}^{2}+{y}^{2}+2x-2y-23=0
- {x}^{2}+{y}^{2}-2x+2y-3=0
- {x}^{2}+{y}^{2}-2x+2y-23=0
- {x}^{2}+{y}^{2}+2x-2y-3=0
- {x}^{2}+{y}^{2}+2x-2y-27=0
Solución:
Para encontrar la ecuación de la circunferencia podemos seguir dos caminos:
- Sustituir en la ecuación ordinaria las coordenadas de ambos puntos y armar un sistema de ecuaciones no lineal
- Calcular el punto medio entre los dos puntos junto a la mitad de la distancia entre ellos para obtener centro y radio
Debido a que los sistemas de ecuaciones no lineales son tediosos de resolver, elegiremos el segundo camino.
Cálculo del centro.
Ya que los puntos pertenecen a la circunferencia, ambos forman un diámetro o cuerda diametral que tiene como característica que su punto medio es el centro.
C\left(\frac{{x}_{a}+{x}_{b}}{2},\frac{{y}_{a}+{y}_{b}}{2}\right)
Sustituimos.
C\left(\frac{-2+4}{2},\frac{3-5}{2}\right)=C\left(1,-1\right)
Cálculo del radio.
El radio es igual a la mitad de la distancia entre los puntos A y B .
r=\frac{\left|AB\right|}{2}=\frac{\sqrt{{\left(-2-4\right)}^{2}+{\left(-5-3\right)}^{2}}}{2}=\frac{10}{2}=5
Sustituimos ambos parámetros en la ecuación ordinaria de la circunferencia.
{\left(x-1\right)}^{2}+{\left(y+1\right)}^{2}={\left(5\right)}^{2}
Desarrollamos.
{x}^{2}-2x+1+{y}^{2}+2y+1=25
Ordenamos.
{x}^{2}+{y}^{2}-2x+2y-23=0
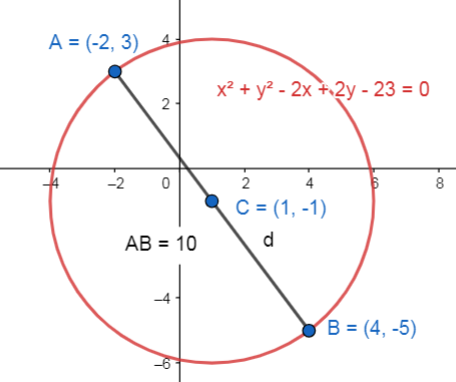
Concluimos seleccionando como correcta a la ecuación del inciso C.
Reactivo 72: Dos rectas atravesadas por una transversal
Los segmentos \underset{\_}{AB} y \underset{\_}{CD} mostrados en el siguiente esquema son paralelos. El valor del ángulo x en grados es _________.
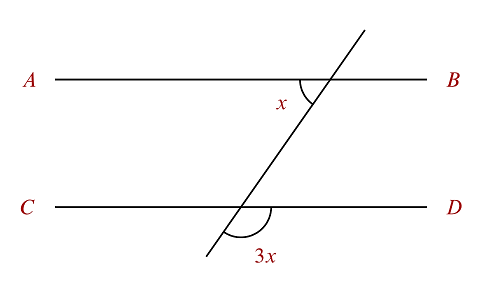
- 22.5°
- 40.5°
- 55°
- 35.5°
- 45°
Solución:
El ángulo externo 3x tiene el mismo valor que el ángulo suplementario a x ya que los segmentos de recta son paralelos entre sí. Ambos ángulos 3x y x suman 180°.
3x+x=180°
De esta sencilla ecuación se despeja x .
4x=180°\to x=45°
El valor del ángulo x en grados es 45°.
Comparando con las opciones, escogemos como correcta a la E.

