¡Nos vemos de nuevo aspirante! Continuamos con la quinta parte de la guía de ingreso resuelta para las divisiones de CBI y CNI del examen de ingreso a la UAM con los reactivos del 53 al 62. Toma descansos entre grupos de reactivos, es necesario para afianzar los conocimientos adquiridos.

Guía UAM Matemáticas Parte 5 resuelta
¡Ya falta poco aspirante! Continuamos con la solución de la quinta parte de los reactivos de matemáticas para las divisiones CBI y CNI, del examen de ingreso a la Universidad Autónoma Metropolitana.
Reactivo 53: División sintética o regla de Ruffini
Al factorizar la expresión 8{x}^{3}-36{x}^{2}+54x-27 el resultado es _____________.
- (2x-3{)}^{2}(2x-3)
- (3x-2{)}^{2}(3x+2)
- (2x-3{)}^{2}(3x+2)
- (3x-2{)}^{2}(2x-3)
- (3x-2{)}^{2}(3x-2)
Solución:
La división sintética permite descomponer a un polinomio como el producto de otros polinomios de menor grado. Antes de ello, debemos dejar al término de mayor grado sin coeficiente y utilizar esa expresión equivalente como la nueva variable del polinomio.
Ya que 8 puede escribirse como {2}^{3} , el polinomio queda de la siguiente manera:
{\left(2x\right)}^{3}-36{x}^{2}+54x-27
Ahora, convertimos a cada término con x en 2x
{\left(2x\right)}^{3}-9\bullet {2}^{2}\bullet {x}^{2}+27\bullet 2x-27={\left(2x\right)}^{3}-9{\left(2x\right)}^{2}+27\left(2x\right)-27
La nueva variable del polinomio es 2x y por conveniencia, la expresaremos como a=2x .
{\left(2x\right)}^{3}-9{\left(2x\right)}^{2}+27\left(2x\right)-27\to {a}^{3}-9{a}^{2}+27a-27
A este nuevo polinomio le podemos aplicar la división sintética de forma sencilla. Escribimos los coeficientes en orden creciente.
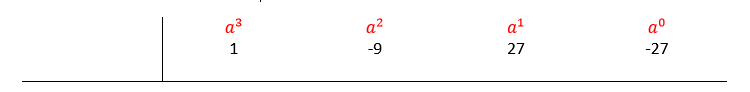
Ahora, probamos colocando un número que sea divisor del término independiente, los candidatos son: 1, 3, 9, -1, -3 y -9. Intentemos con 3. Bajamos el 1, multiplicamos 3 por 1 y el resultado se coloca bajo el coeficiente del siguiente término, es decir -9.
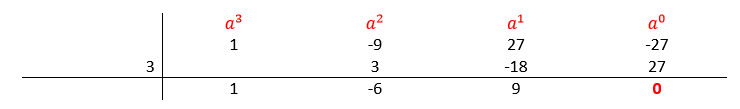
Hemos anulado el término independiente. El polinomio va quedando:
{a}^{3}-9{a}^{2}+27a-27=\left(a-3\right)\left({a}^{2}-6a+9\right)
Debemos factorizar el trinomio cuadrático. El nuevo término independiente es el 9 y sus divisores son 1, 3, -1, -3. Intentemos de nuevo con 3.
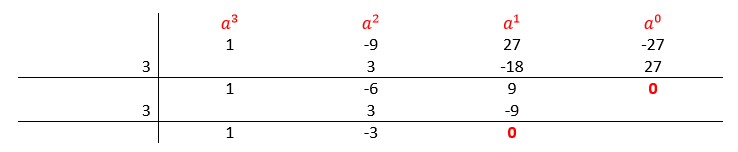
Eliminado el término independiente, no podemos continuar factorizando porque hemos llegado a un resultado lineal. El polinomio quedaría:
{a}^{3}-9{a}^{2}+27a-27=\left(a-3\right)\left(a-3\right)\left(a-3\right)
Sustituimos a=2x .
=\left(2x-3\right)\left(2x-3\right)\left(2x-3\right)
Combinamos dos de los factores lineales como una potencia al cuadrado y concluimos que:
Al factorizar la expresión 8{x}^{3}-36{x}^{2}+54x-27 el resultado es {\left(2x-3\right)}^{2}\left(2x-3\right) .
Escogemos como respuesta correcta a la opción A.
Reactivo 54: Operaciones con fracciones
¿Cuál es el resultado de reducir la fracción \frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{c}+1} a su forma más simple?
- \frac{a+b+c}{abc}
- \frac{a+b}{c+1}
- \frac{c\left(b+a\right)}{ab\left(1+c\right)}
- \frac{1+c}{a+b}
- \frac{\left(1+c\right)\left(b+a\right)}{abc}
Solución:
Primero, resolvemos la suma de fracciones en el numerador y luego en el denominador, para después aplicar la regla del sándwich o de la doble “c”.
Suma de fracciones en el numerador. Empleamos el método del producto cruzado.
\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{c}+1}=\frac{\frac{b+a}{ab}}{\frac{1}{c}+1}
Suma de fracciones en el denominador.
\frac{\frac{b+a}{ab}}{\frac{1}{c}+1}=\frac{\frac{b+a}{ab}}{\frac{1}{c}+\frac{1}{1}}=\frac{\frac{b+a}{ab}}{\frac{1+c}{c}}
Ahora, la regla del sándwich.
\frac{\frac{b+a}{ab}}{\frac{1+c}{c}}=\frac{c\left(b+a\right)}{ab\left(1+c\right)}
Como no hay factores iguales en el numerador y denominador, esta sería la forma simplificada de la expresión.
Concluimos seleccionando como respuesta correcta a la opción C.
Reactivo 55: Fracciones algebraicas
El resultado de simplificar la fracción algebráica \frac{-5{x}^{3}y-20x{y}^{2}}{{x}^{2}+4y} es __________.
- -5xy
- -{x}^{2}-4y
- -{x}^{2}-4{y}^{2}
- -xy
- x+4{y}^{2}
Solución:
Primero, se extrae factor común del numerador el mínimo común múltiplo entre -5{x}^{3}y y -20x{y}^{2} , en este caso es -5xy quedando la fracción como:
\frac{-5{x}^{3}y-20x{y}^{2}}{{x}^{2}+4y}=\frac{-5xy\left({x}^{2}+4y\right)}{{x}^{2}+4y}
Simplificamos a {x}^{2}+4y ya que es un factor común en el numerador y el denominador.
\frac{-5xy\left({x}^{2}+4y\right)}{{x}^{2}+4y}=-5xy
Finalmente:
El resultado de simplificar la fracción algebráica \frac{-5{x}^{3}y-20x{y}^{2}}{{x}^{2}+4y} es -5xy .
Comparando con las opciones, escogemos como respuesta correcta a la A.
Reactivo 56: Fracciones y expresiones radicales
La expresión \frac{1}{\sqrt{2}-1}+\frac{2}{\sqrt{3}+1} es igual a ________________.
- \frac{\sqrt{3}+2\sqrt{2}-1}{\left(\sqrt{2}-1\right)\left(\sqrt{3}+1\right)}
- 3
- \frac{\sqrt{3}+2\sqrt{2}-1}{\left(\sqrt{2}+1\right)\left(\sqrt{3}-1\right)}
- \frac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}-1\right)\left(\sqrt{3}+1\right)}
- \sqrt{2}+\sqrt{3}+\frac{1}{2}
Solución:
Comenzamos por resolver la suma de fracciones mediante el producto cruzado.
\frac{1}{\sqrt{2}-1}+\frac{2}{\sqrt{3}+1}=\frac{\sqrt{3}+1+2\left(\sqrt{2}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{2}-1\right)}
Aplicamos distributiva en el numerador.
\frac{\sqrt{3}+1+2\left(\sqrt{2}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{2}-1\right)}=\frac{\sqrt{3}+1+2\sqrt{2}-2}{\left(\sqrt{3}+1\right)\left(\sqrt{2}-1\right)}
Simplificamos.
\frac{\sqrt{3}+1+2\sqrt{2}-2}{\left(\sqrt{3}+1\right)\left(\sqrt{2}-1\right)}=\frac{\sqrt{3}+2\sqrt{2}-1}{\left(\sqrt{3}+1\right)\left(\sqrt{2}-1\right)}
Comparando con las opciones, escogemos como correcta a la opción A.
Reactivo 57: Simplificación de expresiones
El resultado de simplificar la expresión \frac{{x}^{3}+8}{x+2} es __________.
- {x}^{2}+2x-4
- (x+2{)}^{2}
- {x}^{2}-2x-4
- {x}^{2}-2x+4
- {x}^{2}+4
Solución:
Comenzamos por factorizar el numerador, expresando al 8 como {2}^{3} y luego aplicando la fórmula para la suma de cubos perfectos.
{a}^{3}+{b}^{3}=(a+b)\left({a}^{2}-ab+{b}^{2}\right)
Donde:
- a=x
- b=2
La fracción queda:
\frac{{x}^{3}+{2}^{3}}{x+2}=\frac{\left(x+2\right)\left({x}^{2}-2x+4\right)}{x+2}
Simplificando factor común en el numerador y denominador.
\frac{\left(x+2\right)\left({x}^{2}-2x+4\right)}{x+2}={x}^{2}-2x+4
Comparando con las opciones, escogemos como correcta a la D.
Reactivo 58: Simplificación
Al simplificar la fracción \frac{18{a}^{2}b{c}^{3}}{2a{c}^{5}} , se obtiene __________.
- 18\frac{{a}^{2}b}{{c}^{2}}
- 18\frac{ab}{{c}^{2}}
- 9\frac{ab}{{c}^{2}}
- 9\frac{ab}{c}
- 9\frac{{a}^{2}}{{c}^{2}}
Solución:
Para encontrar la forma simplificada de la expresión, debemos aplicar las respectivas propiedades de los exponentes con los factores que sean comunes en el numerador y denominador, que en este caso son a y c ; además de simplificar 18/2.
\frac{18{a}^{2}b{c}^{3}}{2a{c}^{5}}=9{a}^{2-1}b{c}^{3-5}=9ab{c}^{-2}
Propiedad del exponente negativo.
9ab{c}^{-2}=\frac{9ab}{{c}^{2}}
Finalmente:
Al simplificar la fracción \frac{18{a}^{2}b{c}^{3}}{2a{c}^{5}} , se obtiene \frac{9ab}{{c}^{2}} .
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 59: Problemas matemáticos
Laura gasta un tercio de su salario al pagar la renta; utiliza una quinta parte de lo que le pagan para comprar comida. Con esfuerzos ahorra la décima parte de su sueldo. También destina una décima parte de su salario para pagar transporte. Si después de cubrir todos sus gastos le quedan $800.0, ¿Cuánto gana Laura?
- $1 800
- $2 400
- $4 000
- $1 100
- $3 000
Solución:
Para calcular el salario mensual de Laura, debemos restar a dicha cantidad las fracciones que gasta en cada pago y lo que destina para sus ahorros. Llamaremos x al salario total de Laura.
Gasta \frac{x}{3} en la renta, \frac{x}{5} en comida, \frac{x}{10} para transporte, ahorra \frac{x}{10} del sueldo y le quedan solo $800. Si los gastos y el ahorro se restan del sueldo total, podemos expresar todo en la siguiente ecuación:
Lo que queda=El total-Los gastos-Ahorros
Es decir:
800=x-\left(\frac{x}{3}+\frac{x}{5}+\frac{x}{10}\right)-\frac{x}{10}
Despejamos a x .
800=\frac{4}{15}x\to x=\frac{\left(15\right)\left(800\right)}{4}
x=3000
El sueldo de Laura es de $3 000 al mes.
Finalizamos escogiendo como respuesta correcta a la opción E.
Reactivo 60: Ecuación de la recta
¿Cuál es el valor de k de forma que la recta x-ky=10 pase por el punto \left(0, -5\right) ?
- 10
- 2
- -1
- \frac{1}{2}
- -2
Solución:
Para determinar el valor del parámetro k solo debemos sustituir las coordenadas del punto dado en la ecuación y despejar su valor.
Sustituyendo al punto \left(0, -5\right) .
x-ky=10\to 0-\left(-5\right)k=10
5k=10
k=\frac{10}{5}=2
Concluimos seleccionando como respuesta correcta a la opción B.
Reactivo 61: Lenguaje natural a expresión matemática
Hay 12 manzanas más que naranjas en una canasta con 36 frutas de estos dos tipos ¿Cuál les ecuaciones utilizarías para saber cuántas frutas de cada tipo hay?
( m=número de manzanas, n=número de naranjas .)
- 12m+n=36
- m+n=36
- m-12n=36
- m+n=12
- m-n=12
- 2 y 5
- 1 y 5
- 3 y 4
- 2 y 4
- 3 y 5
Solución:
Debemos transformar las frases que indican las relaciones entre manzanas y naranjas en ecuaciones matemáticas. Comencemos por la primera frase:
Hay 12 manzanas más que naranjas en una canasta…
m=n+12\to m-n=12
Es decir, para obtener el total de manzanas le sumamos 12 a las naranjas.
La frase continúa y dice: con 36 frutas de estos dos tipos…
m+n=36
El total de manzanas y naranjas es 36.
Ambas ecuaciones corresponden a la 5 y 2 respectivamente. Comparando con las opciones, seleccionamos como correcta a la A.
Reactivo 62: Relaciones entre ángulos
El ángulo A es uno de los ángulos agudos de un triángulo rectángulo. Si tan A =\frac{4}{3} , entonces el valor de sin A es ______________.
- 3/5
- 4/5
- 3/4
- 5/3
- 5/4
Solución:
De los temas referentes a la trigonometría, sabemos que la tangente del ángulo es igual al cociente entre el cateto opuesto y el cateto adyacente del triángulo rectángulo.
tan A =\frac{CO}{CA}=\frac{4}{3}
Es decir, la proporción entre el cateto opuesto y el adyacente de los lados del triángulo es 4/3. El menor triángulo con dicha proporción es aquel cuyo cateto opuesto mide 4 unidades y cateto adyacente 3 unidades. Recordemos el teorema de Tales o de triángulos semejantes.
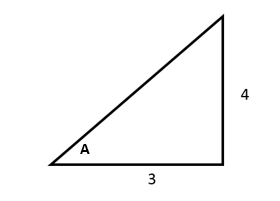
Ya que el seno de un ángulo es igual a su cateto opuesto sobre la hipotenusa, con Pitágoras calculamos el valor de la hipotenusa y hacemos el cociente.
h=\sqrt{{4}^{2}+{3}^{2}}=5
Finalmente:
sin A =\frac{4}{5}
Comparando con las opciones, seleccionamos como correcta a la B.

