¡Felicidades aspirante! Ya vamos por la cuarta parte de la guía de matemáticas resuelta para la UAM en las divisiones de CBI y CNI, en la que vamos a desarrollar del reactivo 43 al 52.

Guía UAM Matemáticas Parte 4 resuelta
Continuamos resolviendo la cuarta parte de los reactivos de matemáticas para el examen de ingreso a la UAM en las divisiones de CBI y CNI.
La prueba ha cambiado de modalidad presencial a modalidad virtual. Adecúa tu espacio de trabajo con los requerimientos necesarios antes del día del examen.
Reactivo 43: Ecuación de la parábola
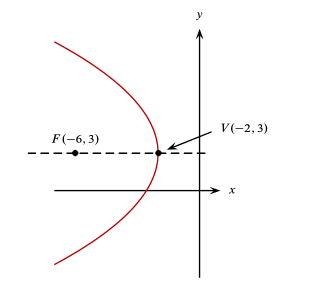
Determinar la ecuación de la parábola de la siguiente figura:
- {y}^{2}-6y+16x-41=0
- {y}^{2}-6y+16x+41=0
- {y}^{2}-6y+16x+40=0
- {y}^{2}-6y+16x+43=0
- {y}^{2}-6y+16x-40=0
Solución:
Antes de pasar a sustituir ciertos valores en la ecuación ordinaria, debemos identificar qué variable debe quedar elevada al cuadrado y el signo de 4p . Como es una parábola que abre paralela al eje x , será y la variable elevada al cuadrado.
Además, ya que abre en dirección de las x negativas 4p debe ser negativo. Por tanto, la ecuación ordinaria que debemos emplear es:
-2p(x-h)={\left(y-k\right)}^{2}
Donde:
- p es la distancia entre el foco y la recta directriz de la parábola o, el doble de la distancia entre el vértice y el foco
- h, k son las coordenadas del vértice de la parábola
A partir de la gráfica, sabemos que las coordenadas del vértice son:
\left(h,k\right)=\left(-\mathrm{2,3}\right)
p se puede calcular como:
p=2\left|VF\right|=2\left|-2-\left(-6\right)\right|=8
Sustituyendo en la ecuación nos queda:
-2\left(8\right)(x+2)={\left(y-3\right)}^{2}
Desarrollamos.
-16(x+2)={y}^{2}-6y+9
-16x-32={y}^{2}-6y+9
{y}^{2}-6y+16x+41=0
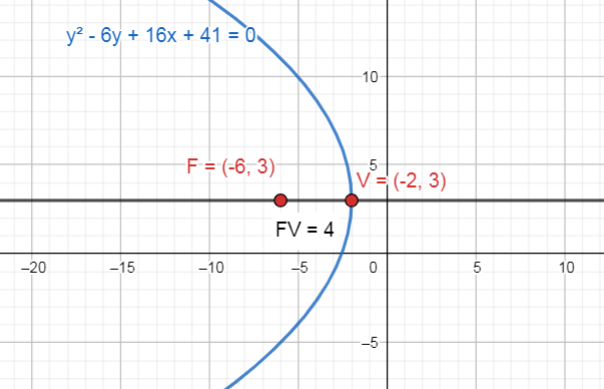
Comparando nuestro resultado con las opciones del problema, escogemos como correcta a la opción B.
Reactivo 44: Comparación de números reales
Considere x=-\frac{1}{2} . Al ordenar los números x, {x}^{2}, {x}^{3} de menor a mayor, se obtiene _______.
- {x}^{3}<{x}^{2}<x
- x<{x}^{2}<{x}^{3}
- x<{x}^{3}<{x}^{2}
- {x}^{2}<x<{x}^{3}
- {x}^{3}<x<{x}^{2}
Solución:
Una forma sencilla de ordenar estos tres números, es determinar el signo y magnitud que poseerá cada uno, partiendo del hecho que {x}^{2} y {x}^{3} son potencias de x .
{x}^{3} es igual a -\frac{1}{2} multiplicado 3 veces, es decir \left(-\frac{1}{2}\right)\left(-\frac{1}{2}\right)\left(-\frac{1}{2}\right)=-\frac{1}{8} . Por otra parte, {x}^{2} es igual a multiplicar -\frac{1}{2} dos veces \left(-\frac{1}{2}\right)\left(-\frac{1}{2}\right)=\frac{1}{4} .
De esta forma, sabemos que el menor de los tres x ya que es negativo pero de mayor magnitud que {x}^{3} situándose más a la izquierda. Luego se encuentra {x}^{3} y el mayor es {x}^{2} . Concluimos que:
x<{x}^{3}<{x}^{2}
Seleccionamos como respuesta correcta a la opción C.
Reactivo 45: Suma de polinomios
¿Cuál es el resultado de sumar el polinomio {x}^{3}y+5{x}^{2}{y}^{2}-3x{y}^{3} con el polinomio 7x{y}^{3}-3{x}^{2}{y}^{2}-2{x}^{3}y ?
- 8{x}^{3}y+2{x}^{2}{y}^{2}-5x{y}^{3}
- 6{x}^{3}y-6{x}^{2}{y}^{2}-x{y}^{3}
- -3{x}^{3}y+8{x}^{2}{y}^{2}+10x{y}^{3}
- {x}^{3}y-2{x}^{2}{y}^{2}-4x{y}^{3}
- -{x}^{3}y+2{x}^{2}{y}^{2}+4x{y}^{3}
Solución:
Para sumar dos polinomios, debemos agrupar los términos que posean iguales literales elevados cada uno al mismo exponente y sumar o restar (según sea el caso) los coeficientes.
\left({x}^{3}y+5{x}^{2}{y}^{2}-3x{y}^{3}\right)+\left(7x{y}^{3}-3{x}^{2}{y}^{2}-2{x}^{3}y\right)
Deshacemos los paréntesis y agrupamos términos semejantes.
{x}^{3}y+5{x}^{2}{y}^{2}-3x{y}^{3}+7x{y}^{3}-3{x}^{2}{y}^{2}-2{x}^{3}y
={x}^{3}y-2{x}^{3}y+5{x}^{2}{y}^{2}-3{x}^{2}{y}^{2}-3x{y}^{3}+7x{y}^{3}
Ahora, sumamos y restamos los coeficientes.
=-{x}^{3}y+2{x}^{2}{y}^{2}+4x{y}^{3}
Concluimos que la suma de ambos polinomios es igual a -{x}^{3}y+2{x}^{2}{y}^{2}+4x{y}^{3} . Comparando con las opciones, escogemos como correcta a la E.
Reactivo 46: División de polinomios
El resultado de \frac{8{x}^{3}-27}{2x-3} es _________.
- 4{x}^{2}-6x+9
- 4{x}^{2}-\frac{27}{2x}-\frac{8{x}^{3}}{3}+9
- 4{x}^{2}+9
- 4{x}^{2}+6x+9
- -4{x}^{2}-6x-9
Solución:
Antes de aplicar el algoritmo de división larga, probemos con factorizar el polinomio del numerador para intentar simplificar alguno de los factores con el binomio del denominador.
\frac{8{x}^{3}-27}{2x-3}Al 8 lo podemos expresar como 2 elevado al cubo y al 27 como 3 al cubo.
\frac{8{x}^{3}-27}{2x-3}=\frac{{\left(2x\right)}^{3}-{3}^{3}}{2x-3}
Podemos aplicar la factorización para una diferencia de cubos:
(a-b)\left({a}^{2}+ab+{b}^{2}\right)={a}^{3}-{b}^{3}
Con a=2x y b=3 , el numerador queda expresado como:
\frac{{\left(2x\right)}^{3}-{3}^{3}}{2x-3}=\frac{\left(2x-3\right)\left(4{x}^{2}+6x+9\right)}{2x-3}
Simplificamos 2x-3 de la fracción.
\frac{\left(2x-3\right)\left(4{x}^{2}+6x+9\right)}{2x-3}=4{x}^{2}+6x+9
Concluimos afirmando que:
El resultado de \frac{8{x}^{3}-27}{2x-3} es 4{x}^{2}+6x+9 .
Comparando con las opciones, escogemos como respuesta correcta a la D.
Reactivo 47: División de polinomios
Al dividir el polinomio {x}^{3}+6{x}^{2}-6x-45 entre el polinomio x+3 , el resultado es __________.
- {x}^{2}+3x-15
- {x}^{2}-6x+75
- {x}^{2}+12x-45
- {x}^{2}+9x+45
- {x}^{2}-2x+15
Solución:
En este caso, debemos aplicar el algoritmo de división sintética para encontrar el resultado.
![]()
Debemos ir colocan en el cociente términos que multiplicados por x , den como resultado al primer elemento del dividendo. Vamos por {x}^{3} , debemos colocar {x}^{2} .
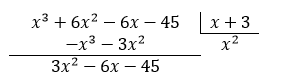
Para el siguiente término, sumamos 3x al cociente.
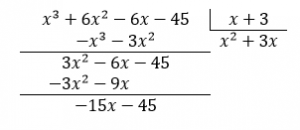
Restamos al cociente 15.
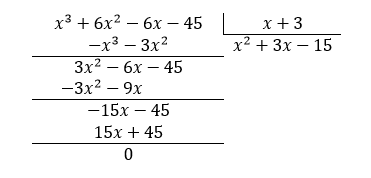
Finalmente:
Al dividir el polinomio {x}^{3}+6{x}^{2}-6x-45 entre el polinomio x+3 , el resultado es {x}^{2}+3x-15 .
Comparando con los incisos, escogemos como respuesta correcta a la A.
Reactivo 48: Radicales
Al calcular \sqrt{(a+b{)}^{2}-{a}^{2}} , se obtiene ___________.
- b\left(2a+b\right)
- \sqrt{{b}^{2}-{a}^{2}}
- b
- \sqrt{2ab}+b
- \sqrt{2ab+{b}^{2}}
Solución:
Comenzamos por desarrollar el producto notable en la expresión radicando.
\sqrt{(a+b{)}^{2}-{a}^{2}}=\sqrt{{a}^{2}+2ab+{b}^{2}-{a}^{2}}
Restamos términos semejantes.
\sqrt{{a}^{2}+2ab+{b}^{2}-{a}^{2}}=\sqrt{2ab+{b}^{2}}
Comparando con las opciones, la respuesta correcta es la E.
Reactivo 49: Producto de binomios
El producto (x-5)(x-3)(x+5)(x+3) es igual a _____________.
- {x}^{4}-16{x}^{2}+225
- {x}^{4}-5{x}^{3}-24{x}^{2}+75x+225
- {x}^{4}-10{x}^{3}+16{x}^{2}+90x-225
- {x}^{4}-6{x}^{3}-16{x}^{2}+150x-225
- {x}^{4}-34{x}^{2}+225
Solución:
Podríamos realizar el producto uno a uno de los binomios, pero esto sería un procedimiento largo y tedioso. Por suerte, tenemos factores que son conjugados entre sí; x-5 es el conjugado de x+5 y x-3 el de x+3 . Los agrupamos y aplicamos diferencia de cuadrados.
{a}^{2}-{b}^{2}=\left(a-b\right)\left(a+b\right)
\left(x-5\right)\left(x-3\right)\left(x+5\right)\left(x+3\right)=\left(x-5\right)\left(x+5\right)\left(x-3\right)\left(x+3\right)
Diferencia de cuadrados.
\left(x-5\right)\left(x+5\right)\left(x-3\right)\left(x+3\right)=\left({x}^{2}-25\right)\left({x}^{2}-9\right)
Ahora, de 4 binomios el producto se ha reducido a 2.
\left({x}^{2}-25\right)\left({x}^{2}-9\right)={x}^{2}\left({x}^{2}-9\right)-25\left({x}^{2}-9\right)
={x}^{4}-9{x}^{2}-25{x}^{2}+225
={x}^{4}-34{x}^{2}+225
Finalmente:
El producto (x-5)(x-3)(x+5)(x+3) es igual a {x}^{4}-34{x}^{2}+225 .
La respuesta correcta es la opción E.
Reactivo 50: Factorización
Al factorizar 36{a}^{2}-4{b}^{2} , se obtiene _________.
- (6a+2b{)}^{2}
- (6a-2b{)}^{2}
- \left(36a+4b\right)\left(a-b\right)
- \left(36a-4b\right)\left(a+b\right)
- \left(6a-2b\right)\left(6a+2b\right)
Solución:
A simple vista, es claro que debemos aplicar diferencia de cuadrados pero antes, debemos expresar a los coeficientes como el cuadrado de un número. El 4 se puede escribir como {2}^{2} y el 36 como {6}^{2} por tanto:
36{a}^{2}-4{b}^{2}={\left(6a\right)}^{2}-{\left(2b\right)}^{2}
Diferencia de cuadrados:
{\left(6a\right)}^{2}-{\left(2b\right)}^{2}=\left(6a-2b\right)\left(6a+2b\right)
Concluimos que:
Al factorizar 36{a}^{2}-4{b}^{2} , se obtiene \left(6a-2b\right)\left(6a+2b\right) .
La respuesta correcta es la opción E.
Reactivo 51: Fracciones algebraicas
La fracción algebraica \frac{{x}^{2}-5x+6}{{x}^{2}+2x-15} es igual a ________.
- \frac{\left(x-3\right)\left(x-2\right)}{\left(x-3\right)\left(x+5\right)}
- \frac{\left(x+3\right)\left(x-2\right)}{\left(x-3\right)\left(x+5\right)}
- \frac{\left(x-3\right)\left(x+2\right)}{\left(x+3\right)\left(x-5\right)}
- \frac{\left(x-3\right)\left(x+2\right)}{\left(x-3\right)\left(x-5\right)}
- \frac{\left(x+3\right)\left(x-2\right)}{\left(x+3\right)\left(x-5\right)}
Solución:
Debemos encontrar la forma factorizada de los polinomios del numerador y el denominador en la fracción. Existen varios métodos para encontrar la forma factorizada, en este caso usaremos factorización de la forma {x}^{2}+bx+c=\left(x+z\right)\left(x+w\right) donde:
z+w=b
z\bullet w=c
Comenzamos por el polinomio del numerador:
{x}^{2}-5x+6
Dos números que multiplicados den 6 son -2 y -3, para que además sumados sean iguales a -5.
\left(-2\right)\left(-3\right)=6
-2-3=-5
{x}^{2}-5x+6=\left(x-2\right)\left(x-3\right)
Hacemos lo mismo con el denominador:
{x}^{2}+2x-15
Los números respectivos son -3 y 5.
\left(-3\right)\left(5\right)=-15
-3+5=2
{x}^{2}+2x-15=\left(x-3\right)\left(x+5\right)
Sustituyendo en la fracción queda:
\frac{{x}^{2}-5x+6}{{x}^{2}+2x-15}=\frac{\left(x-2\right)\left(x-3\right)}{\left(x-3\right)\left(x+5\right)}
La fracción algebraica \frac{{x}^{2}-5x+6}{{x}^{2}+2x-15} es igual a \frac{\left(x-2\right)\left(x-3\right)}{\left(x-3\right)\left(x+5\right)} .
Comparando con las opciones, seleccionamos como correcta a la A.
Reactivo 52: Diferencia de cuadrados
La expresión {x}^{8}-{y}^{16} puede escribirse como __________.
- \left({x}^{8}+{y}^{8}\right)\left(1-{y}^{8}\right)
- \left({x}^{8}-{y}^{8}\right)\left(1-{y}^{8}\right)
- \left({x}^{4}-{y}^{16}\right)\left({x}^{4}+1\right)
- \left({x}^{4}+{y}^{16}\right)\left({x}^{4}-1\right)
- \left({x}^{4}+{y}^{8}\right)\left({x}^{4}-{y}^{8}\right)
Solución:
Primero, expresamos a cada término como una potencia elevada al cuadrado, es decir como potencia de una potencia:
{x}^{8}-{y}^{16}={\left({x}^{4}\right)}^{2}-{\left({y}^{8}\right)}^{2}
Ahora, aplicamos la diferencia de cuadrados.
{\left({x}^{4}\right)}^{2}-{\left({y}^{8}\right)}^{2}=\left({x}^{4}-{y}^{8}\right)\left({x}^{4}+{y}^{8}\right)
Por propiedad conmutativa de la multiplicación:
\left({x}^{4}-{y}^{8}\right)\left({x}^{4}+{y}^{8}\right)=\left({x}^{4}+{y}^{8}\right)\left({x}^{4}-{y}^{8}\right)
Finalmente:
La expresión {x}^{8}-{y}^{16} puede escribirse como \left({x}^{4}+{y}^{8}\right)\left({x}^{4}-{y}^{8}\right) .
Escogemos como respuesta correcta a la opción E.

