¡Seguimos con la tercera parte! En este post vamos a resolver los reactivos del 33 al 42 de la tercera parte en la guía de matemáticas UAM para las divisiones de Ciencias Básicas e Ingeniería y Ciencias Naturales e Ingeniería.

Si aún no resuelves los reactivos por tu cuenta, hazlo y luego regresa. Utiliza este material como consulta o para salir de dudas.
Guía UAM Matemáticas Parte 3 resuelta
Vamos con la solución paso a paso de la tercera parte de los reactivos de matemáticas para las divisiones de CBI y CNI.
Los reactivos se han dividido en secciones de 10 para que tomes un descanso entre grupos. Esto último es importante para que puedas sentar los conocimientos adquiridos.
Reactivo 33: Porcentajes y proporciones
Si el 55% de los habitantes de la ciudad tiene automóvil y las 2/5 partes de ellos no lo utilizan el fin de semana ¿Qué porcentaje de los habitantes no utiliza auto el fin de semana?
- 45%
- 88%
- 22%
- 33%
- 67%
Solución:
Ya que dos quintas partes (2/5) de los habitantes que tienen automóvil no lo utilizan el fin de semana, podemos calcular el porcentaje de habitantes con auto que no lo utilizan el fin de semana multiplicando 2/5 por 55%.
P=55\%\bullet \frac{2}{5}=22\%
El 22% de los habitantes tienen automóvil y no lo utilizan el fin de semana.
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 34: Integral indefinida
Calcula la integral:
\int \left(5{x}^{4}-3{x}^{-4}+1\right)dx
- {x}^{5}+{x}^{-3}+x+C
- 20{x}^{3}+12{x}^{-5}+C
- 5{x}^{5}-3{x}^{-3}+x+C
- 20{x}^{3}-12{x}^{-5}+C
- {x}^{4}+\frac{3}{5}{x}^{-5}+x+C
Solución:
Para calcular la primitiva de la función integrando, debemos decidir con qué método de integración comenzar en base a las características de la misma.
En este caso, se trata de una función cuyos términos son: un monomio de cuarto grado, una función fracción y un término independiente, por tanto no será necesario recurrir a un método específico. Separaremos la integral en 3 y luego aplicamos las fórmulas de integración directa.
Propiedad de la integral de la suma.
\int \left(5{x}^{4}-3{x}^{-4}+1\right)dx=\int 5{x}^{4}dx-\int 3{x}^{-4}dx+\int dx
Aplicamos la fórmula de integral de una potencia e integral del diferencial.
\int 5{x}^{4}dx-\int 3{x}^{-4}dx+\int dx=\frac{5{x}^{4+1}}{4+1}-\frac{3{x}^{-4+1}}{-4+1}+x+C
=\frac{5}{5}{x}^{5}+\frac{3}{3}{x}^{-3}+x+C
={x}^{5}+{x}^{-3}+x+C
Concluimos que:
\int \left(5{x}^{4}-3{x}^{-4}+1\right)dx={x}^{5}+{x}^{-3}+x+C
Comparando con las opciones, seleccionamos a la A como la respuesta correcta.
Reactivo 35: Porcentajes y proporciones
¿Qué tanto por ciento de 80\frac{1}{3} es 20\frac{1}{12} ?
- 10%
- 25%
- 15%
- 20%
- 30%
Solución:
Para calcular el porcentaje, debemos hacer el cociente de 20\frac{1}{12} sobre 80\frac{1}{3} y luego multiplicarlo por 100%, es decir aplicar la definición de porcentaje:
\%=\frac{{N}_{\%}}{N}*100\%
Pero antes, debemos decidir si vamos utilizar las fracciones mixtas o en su forma pura. En este caso, lo haremos en fracciones puras y por ende, debemos transformarlas.
20\frac{1}{12}=20+\frac{1}{12}=\frac{20\bullet 12+1}{21}=\frac{241}{12}
80\frac{1}{3}=80+\frac{1}{3}=\frac{80\bullet 3+1}{3}=\frac{241}{3}
Ahora, procedemos a sustituir la fórmula de porcentaje. \frac{241}{12} va en el numerador y \frac{241}{3} en el denominador.
\%=\frac{\frac{241}{12}}{\frac{241}{3}}*100=25\%
Concluimos que: 20\frac{1}{12}=\frac{241}{12} representa el 25% de 80\frac{1}{3}=\frac{241}{3} .
Comparando con las opciones, escogemos como respuesta correcta a la B.
Reactivo 36: Porcentajes
Un banco ofrece el 5% de interés semestral ¿Cuánto esperas tener en este banco en un año, si depositaste $1 000.00 y no retiraste los intereses?
- $1 050.00
- $1 102.50
- $1 100.00
- $1 210.50
- $1. 100.50
Solución:
El 5% de intereses semestral implica que cada seis meses, el saldo en la cuenta bancaria aumenta un 5%, si la proyección se realiza para un año en los primeros 6 meses se obtiene un 5% del saldo, es decir:
\$1000.00*105\%=\$1050.00
Al finalizar el segundo semestre del año, se obtiene el otro 5% en intereses. Debemos calcular el 105% del saldo acumulado que, como no hubo ningún retiro y suponemos tampoco otro ingreso externo se mantiene en $1 050.00.
\$1050.00*105\%=\$1102.5
Comparando con las opciones, escogemos a B como la respuesta correcta.
Reactivo 37: Valor numérico de una expresión
Calcula el valor numérico de la expresión \frac{3{m}^{2}}{\sqrt{2n}} , cuando m=-3 y n=2 .
- \frac{27}{2}
- \frac{9}{4}
- -\frac{27}{2}
- \frac{9}{2}
- \frac{12}{2}
Solución:
Primero, sustituimos el valor numérico de m y n en la expresión dada.
\frac{3{\left(-3\right)}^{2}}{\sqrt{2\left(2\right)}}
Calculamos el cuadrado de -3 y resolvemos el producto dentro de la raíz.
\frac{3{\left(-3\right)}^{2}}{\sqrt{2\left(2\right)}}=\frac{3\bullet 9}{\sqrt{4}}
Por último, simplificamos el producto en el numerador y resolvemos la raíz del denominador.
\frac{3\bullet 9}{\sqrt{4}}=\frac{27}{2}
Comparando nuestro resultado con los incisos, seleccionamos como correcto al A.
Reactivo 38: Desigualdades
Si x es un entero negativo ¿Cómo se ordenan j, k, l de menor a mayor?
j=1-x k=x-1 l=(1-x)+(x-1)
- k<j<l
- k<l<j
- l<j<k
- j<k<l
- l<k<j
Solución:
Analizaremos cada expresión para determinar el signo y luego comparar a las variables entre sí.
j=1-x
Ya que x es negativo, si se multiplica por -1 el resultado será un número positivo que se suma con el 1, por tanto: j>0 .
k=x-1
Como x es negativo, si se le resta 1 el resultado será un número más negativo, por tanto k<0 .
l=(1-x)+(x-1)
Extraemos factor común menos del segundo término.
l=\left(1-x\right)-(1-x)
El resultado de restar dos números iguales es cero, por tanto:
l=0
Podemos concluir que: k es un número negativo, j es positivo y l es igual a cero. Ordenados de forma creciente quedarían: k\to l\to j . Expresado como una desigualdad:
k<l<j
Comparando con las opciones, seleccionamos como respuesta correcta a la opción B.
Reactivo 39: Mínimo común múltiplo
El mínimo común múltiplo (mcm) de los números 30, 20 y 50 es ________.
- 10
- 50
- 20
- 300
- 30 000
Solución:
Para calcular el mcm de un conjunto de números, debemos descomponerlos en factores y realizar el producto de aquellos factores de potencia mayor.
Descomponiendo en factores al 30:
30=2\bullet 5\bullet 3
Descomponiendo en factores al 20:
20={2}^{2}\bullet 5
Descomponemos en factores al 50:
50=2\bullet {5}^{2}
En este caso, los factores de mayor potencia son: {2}^{2}, {5}^{2} y 3, por tanto el mcm es:
mcm\left(30, 20, 50\right)={2}^{2}\bullet {5}^{2}\bullet 3=300
Finalizamos seleccionando como respuesta correcta al inciso D.
Reactivo 40: Orden de las operaciones
Al eliminar los paréntesis en la expresión -\left[\right(a+b)-(2a-b\left)\right]-(2a-b) el resultado es ________.
- -a+b
- a-2b
- -a-b
- a-b
- -a+2b
Solución:
Para deshacer los corchetes y paréntesis en la expresión, debemos aplicar distributiva del signo que se encuentra a la izquierda del término. En el primero, deshacemos los corchetes multiplicando el menos por los elementos internos.
-\left[\left(a+b\right)-\left(2a-b\right)\right]-\left(2a-b\right)=-\left(a+b\right)+\left(2a-b\right)-\left(2a-b\right)
Podríamos directamente hacer lo mismo con los paréntesis pero, el segundo y tercer término son iguales pero con signos diferentes, por tanto su resta es igual a cero.
-\left(a+b\right)+\left(2a-b\right)-\left(2a-b\right)=-\left(a+b\right)
Luego de esta simplificación, podemos deshacer los paréntesis aplicando propiedad distributiva con el signo menos.
-\left(a+b\right)=-a-b
Comparando nuestro resultado con las opciones, escogemos como respuesta correcta a la C.
Reactivo 41: Gráfica de una parábola
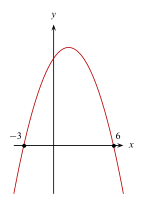
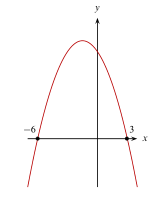
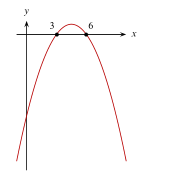
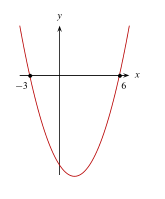
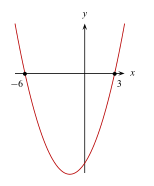
La gráfica de la parábola definida por la ecuación y={x}^{2}-3x-18 está representada en la opción ______.
Solución:
Para determinar la gráfica que representa a la parábola y={x}^{2}-3x-18 debemos identificar dos cosas: hacia donde abre y cuáles son sus puntos de corte. El sentido nos lo da el signo del término cuadrático, en este caso es positivo y por ende, abre paralela al eje y y hacia arriba.
Esto reduce la respuesta a las opciones D y E. Los puntos de corte con el eje x se calculan igualando a cero la ecuación de la parábola.
{x}^{2}-3x-18=0
Resolvemos aplicando la fórmula de segundo grado.
x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
Con:
a=1, b=-3, c=-18
Sustituimos y resolvemos.
x=\frac{-\left(-3\right)\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-18\right)}}{2\left(1\right)}=\frac{3\pm \sqrt{81}}{2}
{x}_{1}=\frac{3+9}{2}=6
{x}_{2}=\frac{3-9}{2}=-3
Concluimos que: la parábola debe abrir hacia arriba y cortar en x=-3 y x=6 .
Comparando con las gráficas de los incisos, nuestro resultado concuerda con el del inciso D.
Reactivo 42: Operaciones con potencias
El valor que se obtiene de {\left[{\left(\frac{2}{8}\right)}^{\frac{1}{2}}\right]}^{-3} es __________.
- \frac{1}{4}
- \frac{1}{8}
- 4
- 8
- 2
Solución:
Para encontrar el valor de la expresión, debemos aplicar primero la propiedad de potencia de una potencia, luego la del exponente negativo y por último evaluar el exponente.
Potencia de una potencia: se multiplican los exponentes.
{\left[{\left(\frac{2}{8}\right)}^{\frac{1}{2}}\right]}^{-3}={\left(\frac{2}{8}\right)}^{\frac{1}{2}*-3}={\left(\frac{2}{8}\right)}^{-\frac{3}{2}}
Exponente negativo: se cambia de signo el exponente y se invierte de lugar al numerador y denominador de la base.
{\left(\frac{2}{8}\right)}^{-\frac{3}{2}}={\left(\frac{8}{2}\right)}^{\frac{3}{2}}
Antes de continuar, podemos simplificar la fracción.
{\left(\frac{8}{2}\right)}^{\frac{3}{2}}={\left(4\right)}^{3/2}
Por último, escribimos al exponente racional como raíz y potencia.
{\left(4\right)}^{3/2}=\sqrt{{4}^{3}}
Resolvemos la potencia y luego la raíz.
\sqrt{{4}^{3}}=\sqrt{64}=8
Concluimos que:
El valor que se obtiene de {\left[{\left(\frac{2}{8}\right)}^{\frac{1}{2}}\right]}^{-3} es 8.
Comparando con las opciones, seleccionamos como respuesta correcta a la D.