¡Saludos aspirante! Esta es la primera parte de la guía de Física UAM para las divisiones de Ciencias Básicas e Ingeniería y Ciencias Naturales e Ingeniería. Resolveremos paso a paso los reactivos del 84 al 95, apoyados de imágenes y recordando los conceptos físicos básicos.

Antes de ver la solución de los ejercicios, te recomiendo desarrollarlos por tu cuenta. La clave para entender física, radica en el claro entendimiento de los conceptos.
Te dejo un resumen de la convocatoria UAM 2022 con la información más resaltante.
- Número de convocatorias: Dos al año.
- Fechas de registro: marzo y agosto del 2022
- Oferta académica: 82 carreras
- Divisiones académicas: 6
- Modalidad: en línea
Estructura del examen de ingreso UAM 2022
El examen de ingreso esta dividido en dos partes: prueba de aptitud y prueba de conocimientos específicos. La primera, consta de preguntas sobre Razonamiento Matemático y Razonamiento Verbal, con una extensión total de 40 reactivos.
El contenido de la segunda parte depende de la división a la que pertenezca tu carrera. En el caso de CBI y CNI, las preguntas constan de física, matemáticas, química, Razonamiento simbólico-abstracto y Razonamiento Lógico.
De forma muy resumida, puedes consultar los subtemas que van para cada una de las asignaturas antes mencionadas.
Física
- Análisis dimensional
- Cinemática
- Dinámica
- Estática
- Hidrostática
- Electrostática
Matemáticas
- Aritmética
- Álgebra
- Racionalización
- Geometría euclidiana
- Trigonometría plana
- Geometría analítica
- Cálculo diferencial e integral
Química
- Materia
- Estructura del átomo
- Nomenclatura
- Reacciones químicas
Resumen de reactivos por cada parte del examen.
| Área | Reactivos | Porcentaje |
|---|---|---|
| Razonamiento verbal | 20 | 25% |
| Razonamiento matemático | 20 | 25% |
| Conocimientos específicos | 40 | 50% |
| Total | 80 | 100% |
Temario de Física para CBI y CNI
El temario puede parecer extenso, pero si estudias con tiempo y organizas tus jornadas de estudio, te aseguro que podrás cubrirlo en su totalidad.
Análisis dimensional
- Sistema internacional de unidades (SI)
- Magnitudes físicas. Escalares y vectoriales. Fundamentales y derivadas
- Notación científica
- Conversión de unidades
Cinemática
- Conceptos de desplazamiento, velocidad y aceleración
- Movimiento rectilíneo uniforme y acelerado
- Movimiento bidimensional: circular y tiro parabólico
Dinámica
- Conceptos de inercia, torca o momento de una fuerza, energía cinética, energía potencial, trabajo y potencia
- Leyes de Newton
Estática
- Diagrama de cuerpo libre
- Equilibrio y centro de gravedad
Hidrostática
- Principio de Pascal
- Densidad
Electrostática
- Carga eléctrica
- Ley de Coulomb
Guía UAM de Física resuelta
Ahora pasamos con la solución de la primera parte de la guía de física para las divisiones de CBI y CNI de la prueba de ingreso a la Universidad Autónoma Metropolitana.
Reactivo 84: Conversión de unidades
Un corredor olímpico logra una velocidad promedio de 10 metros por segundo en la carrera de 100 metros planos ¿Cuál es esa velocidad expresada en kilómetros?
- 3.6 km/h
- 6.6 km/h
- 36 km/h
- 16 km/h
- 6.3 km/h
Solución:
En este caso, el problema solicita que expresemos una velocidad que se encuentra en metros por segundo (m/s) a kilómetros por hora (km/h). Debemos hacer una conversión de unidades, pasar los segundos a horas y los metros a kilómetros.
Sabemos que:
Un kilómetro son mil metros.
1 Km\to 1000 m
Una hora son 3600 segundos.
1 h\to 3600 s
Para convertir, tomamos la cantidad y la multiplicamos por los respectivos factores de conversión que permitan obtener km de metros y horas de segundos.
10\frac{m}{s}\bullet \frac{3600 s}{1 h}\bullet \frac{1 km}{1000 m}
Con la primera fracción \frac{3600 s}{1 h} se eliminan los segundos y quedan horas, mientras que con la segunda \frac{1 km}{1000 m} se eliminan los metros y quedan los kilómetros.
10\frac{m}{s}\bullet \frac{3600 s}{1 h}\bullet \frac{1 km}{1000 m}=\frac{36000 m}{h}\bullet \frac{1 km}{1000 m}=36\frac{km}{h}
Concluimos seleccionando como respuesta correcta a la opción C.
Reactivo 85: Conversión de unidades, masa
Si 1 kilogramo (kg) equivale a 2.20 libras (lb), calcula el equivalente de la masa de un cuerpo de 2.20 kg en libras.
- 4.40 lb
- 4.20 lb
- 1.00 lb
- 2.20 lb
- 4.84 lb
Solución:
El ejercicio en el enunciado nos da la equivalencia entre kg y libras y además, solicita que transformemos 2.20 kg a libras.
Debemos multiplicar a 2.20 kg por un factor de conversión que tenga en el numerador libras y en el denominador kg, de esa manera kg se elimina con kg y quedan solo libras.
2.20 kg\bullet \frac{2.20 lb}{1 kg}
Kilogramo elimina a kilogramo y quedan libras.
2.20 kg\bullet \frac{2.20 lb}{1 kg}=4.84 lb
Comparando nuestro resultado con los incisos, seleccionamos como correcta a la opción E.
Reactivo 86: Conversión de unidades, volumen
¿Cuántos {m}^{3} son 1 200 {cm}^{3} ? ( 1{m}^{3}=1000000{cm}^{3} ).
- 12{m}^{3}
- 0.12{m}^{3}
- 0.012{m}^{3}
- 0.0012{m}^{3}
- 1.2{m}^{3}
Solución:
Debemos convertir de {cm}^{3} a {m}^{3} , por tanto el factor de conversión debe tener en el numerador {m}^{3} y en el denominador {cm}^{3} .
1 200 {cm}^{3}\bullet \frac{1 {m}^{3}}{1 000 000{ cm}^{3}}
Centímetro cúbico se va con centímetro cúbico y nos quedan metros cúbicos.
1 200 {cm}^{3}\bullet \frac{1 {m}^{3}}{1 000 000{ cm}^{3}}=0.0012 {m}^{3}
Comparando con las opciones, la respuesta correcta es la opción D.
Reactivo 87: Inercia
La propiedad de los cuerpos por la que tienden a permanecer en su estado de reposo o de movimiento rectilíneo uniforme, se llama __________.
- Velocidad
- Inercia
- Fuerza
- Equilibrio
- Aceleración
Solución:
La inercia es una propiedad de los cuerpos en reposo o en MRU relativo a un observador, que los hace permanecer en ese estado. Inercia alude a resistencia, pudiendo entender a la inercia de un cuerpo como la resistencia que este opone al cambio de velocidad o de la dirección de su movimiento.
En base a esta definición, indicamos que el término que completa la frase correctamente es la opción B inercia.
La propiedad de los cuerpos por la que tienden a permanecer en su estado de reposo o de movimiento rectilíneo uniforme, se llama inercia.
Reactivo 88: Aceleración promedio
Si un objeto cambia su velocidad de 8 m/s a 16 m/s en 4 s, su aceleración media es de ________.
- 8m/{s}^{2}
- 4m/{s}^{2}
- 1m/{s}^{2}
- 2m/{s}^{2}
- 5m/{s}^{2}
Solución:
La fórmula de la aceleración media o aceleración promedio es:
\overrightarrow{a}=\frac{{\overrightarrow{v}}_{2}-{\overrightarrow{v}}_{1}}{{t}_{2}-{t}_{1}}
La flecha en la parte superior indica que es una magnitud vectorial. Aunque en el problema no se establece una dirección para la velocidad (que también es vectorial) asumimos que es unidireccional y por tanto prescindimos del uso de vectores.
La velocidad 1 es 8 m/s y la velocidad en el instante 2 es 16 m/s. Además, el intervalo de tiempo en el que ocurre el incremento de velocidad \Delta t={t}_{2}-{t}_{1} es de 4 s. Sustituyendo nos queda:
{a}_{m}=\frac{{v}_{2}-{v}_{1}}{{t}_{2}-{t}_{1}}=\frac{16\frac{m}{s}-8\frac{m}{s}}{4 s}=2\frac{m}{{s}^{2}}
Concluimos seleccionando como respuesta correcta a la opción D.
Reactivo 89: Caída libre de cuerpos
Un objeto de 1 kg de masa se deja caer desde un puente y su tiempo de caída libre es de 2 s. Otro objeto del doble de masa se deja caer en las mismas condiciones, y su tiempo de caída libre es _______.
- 1 s
- 4 s
- 9.8 s
- 0.5 s
- 2 s
Solución:
En caída libre, los cuerpos son acelerados hacia el centro de la tierra por acción del campo gravitacional. La magnitud de dicha aceleración es igual a la gravedad terrestre y el desplazamiento resultante es un movimiento uniformemente acelerado.
Sin considerar la resistencia al viento de los cuerpos, es decir una caída libre ideal, el tiempo que tardan dos cuerpos de diferente masa en caer desde una altura inicial {y}_{o} es el mismo.
Esto lo vemos reflejado en la ecuación de posición para una caída libre:
y={y}_{0}-\frac{1}{2}g{t}^{2}
Si la altura final es cero y=0 m (el suelo) la ecuación queda como:
0={y}_{0}-\frac{1}{2}g{t}^{2}\to \frac{1}{2}g{t}^{2}={y}_{o}
\therefore t=\sqrt{\frac{2{y}_{o}}{g}}
El tiempo de caída solo depende de la altura desde la que se deja caer el cuerpo.
En base a todo el análisis, concluimos indicando que el tiempo de caída del otro cuerpo es el mismo que el primero (por realizarse en las mismas condiciones): 2 s. Comparando con las opciones, la respuesta correcta es la E.
Reactivo 90: Movimiento Circular Uniforme
Un objeto describe una trayectoria circular recorriendo un ángulo de \frac{\pi }{2} radianes (rad) en 2 segundos (s) ¿Cuál es su velocidad angular media?
- 2\pi rad/s
- 4\pi rad/s
- \frac{\pi }{4}rad/s
- \frac{\pi }{2}rad/s
- \pi rad/s
Solución:
La velocidad angular media, al igual que la velocidad rectilínea media, es una cantidad que relaciona el cambio de posición (en este caso posición angular) en un intervalo de tiempo.
{\omega }_{m}=\frac{\Delta \theta }{\Delta t}=\frac{{\theta }_{2}-{\theta }_{1}}{{t}_{2}-{t}_{1}}
En este caso, el cambio de posición angular \Delta \theta es igual a \frac{\pi }{2} radianes y el intervalo de tiempo \Delta t en el que se da dicho cambio es de 2 s. Sustituimos y calculamos.
{\omega }_{m}=\frac{\Delta \theta }{\Delta t}=\frac{\frac{\pi }{2}rad}{2 s}=\frac{\pi }{4} rad/s
Comparando con las opciones, concluimos escogiendo como respuesta correcta a la opción C.
Reactivo 91: Movimiento Circular Uniforme
¿Cuál o cuáles de los siguientes ejemplos representan ejemplos de movimientos circulares uniformes?
- El de un proyectil
- El de la rueda de la fortuna
- El de un columpio
- 2
- 1
- 1 y 2
- 2 y 3
- 3
Solución:
Para encontrar la(s) respuesta(s) correcta(s), analizaremos cada situación y determinaremos si es o no un MCU. Recordemos que un MCU es un movimiento circular a velocidad angular constante.
El de un proyectil.
Este movimiento tiene su propia clasificación denominada: Lanzamiento de Proyectiles. Tiene una trayectoria parabólica debido a la acción de la gravedad sobre un proyectil disparado a un determinado ángulo.
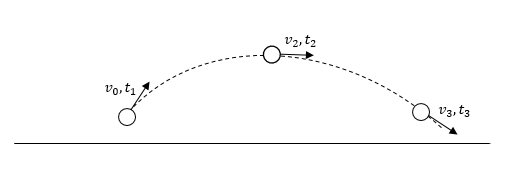
La rueda de la fortuna.
Sin considerar el arranque y el frenado de la rueda, el movimiento que sigue es circular uniforme ya que se mueve en una misma dirección y sin cambiar la velocidad.
Un columpio.
Aunque el columpio se encuentre pivotado en una barra horizontal elevada y aprovechando la tensión de la cadena describe movimientos similares a una sección circular.
El movimiento acelera y desacelera por el impulso de quien se columpia y por acción de la fricción, respectivamente, por tanto no es MCU sino un movimiento armónico simple (considerando un caso ideal). Es más bien similar al de un péndulo.
En base al análisis hecho en las tres situaciones, seleccionamos como correcta a la opción 2, que corresponde al inciso A.
Reactivo 92: Gráficas de velocidad y aceleración
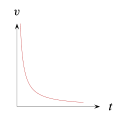
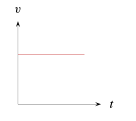
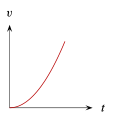
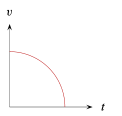
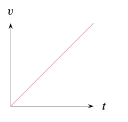
La gráfica de velocidad \left(v\right) contra tiempo \left(t\right) , para un objeto que se mueve con aceleración positiva constante; es _________.
Solución:
Ya que la aceleración mide el cambio de la velocidad respecto del tiempo, si hacemos que el intervalo de tiempo tienda a cero:
\overrightarrow{a}\left(t\right)=\frac{\Delta \overrightarrow{v}\left(t\right)}{\Delta t}
Obtenemos a la aceleración instantánea \overrightarrow{a}\left(t\right) , que puede expresarse como la derivada respecto del tiempo de la velocidad:
\overrightarrow{a}\left(t\right)=\frac{d\overrightarrow{v}\left(t\right)}{dt}
Ahora, para que la aceleración sea una constante positiva +k , la velocidad debe ser una recta con pendiente positiva, ya que la derivada de una recta es igual a su pendiente.
\overrightarrow{a}\left(t\right)=\frac{d\left(kt\right)}{dt}\widehat{u}=k \widehat{u}
Nota: \widehat{u} es un vector unitario del sistema de referencia.
La única gráfica que es una recta con pendiente positiva es la del inciso E, el resto son: una función inversa, una constante (cuya derivada es cero), una parábola y una sección circular. Finalizamos indicando que la respuesta correcta es la E.
Reactivo 93: Trabajo y la energía
La suma de la energía _______ y la energía _______ de un cuerpo se denomina energía ________.
- Eléctrica – potencial – mecánica
- Mecánica – cinética – potencial
- Potencial – mecánica – cinética
- Cinética – potencial – mecánica
- Cinética – eléctrica – potencial
Solución:
La energía es una cantidad que permite a los cuerpos interaccionar con otros o con su ambiente. Existen diferentes formas de energía y una de ellas es la energía mecánica, aquella que permite la interacción entre cuerpos por el movimiento o la posición dentro de un campo de fuerzas.
La energía mecánica es igual a la suma de la energía cinética, aquella que adquieren los cuerpos en movimiento y la energía potencial, aquella que adquieren los cuerpos por su posición en un campo de fuerzas, como la gravitatoria o la fuerza elástica.
En base a lo anterior, completamos la frase con los términos cinética – potencia – mecánica que se encuentran en el inciso D.
La suma de la energía cinética y la energía potencial de un cuerpo se denomina energía mecánica.
Reactivo 94: Fuerzas externas
Debido a la inercia de los cuerpos, un bloque que se desliza sobre una superficie horizontal sin fricción _____________.
- Se desacelera
- Se acelera
- Aumenta su velocidad
- Conserva su estado de movimiento
- Cambia su estado de movimiento
Solución:
En esta situación, donde no existe la influencia de una fuerza externa como la fricción, por acción de la inercia, el cuerpo conservará el estado de movimiento.
Recordemos que la inercia es la cualidad que posee un cuerpo de mantener su estado de reposo o de movimiento si no existe la presencia de una fuerza externa. Como la superficie horizontal no posee fricción, el bloque conserva su estado de movimiento.
Concluimos el ejercicio seleccionando como respuesta correcta a la opción D.
Reactivo 95: Segunda ley de Newton
Un objeto de masa m cuelga de una cuerda que ejerce una tensión T=mg/2 ¿Cuál es la aceleración del objeto?
- \frac{g}{2} hacia arriba
- g hacia abajo
- 2g hacia abajo
- g hacia arriba
- \frac{g}{2} hacia abajo
Solución:
Para establecer todas las fuerzas que intervienen en la situación planteada por el problema, hacemos el diagrama de cuerpo libre del objeto.
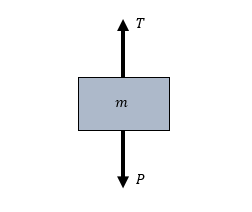
Las únicas fuerzas que intervienen son: el peso en dirección hacia abajo -\widehat{j} y la tensión de la cuerda en dirección hacia arriba +\widehat{j} . La segunda ley de Newton del movimiento dice que:
{\sum }_{}^{}\overrightarrow{F}=m\overrightarrow{a}
La sumatoria de todas las fuerzas es igual a la masa del cuerpo por su aceleración.
Sustituimos:
\overrightarrow{T}-\overrightarrow{P}=m\overrightarrow{a}
\frac{mg}{2}-mg=m {a}_{y}
{a}_{y} indica que estamos trabajando con la componente y de la aceleración. Despejamos:
-\frac{mg}{2}=m {a}_{y}
\therefore {a}_{y}=-\frac{g}{2}
La aceleración tiene como magnitud \frac{g}{2} con dirección hacia abajo.
Comparando con las opciones, escogemos como correcta a la E.