Bienvenido a esta segunda parte de nuestra guía del IPN enfocada en la resolución de ejercicios de Razonamiento matemático. Joven aspirante, si has llegado hasta acá, realmente eres una persona interesada en prepararte para tu futuro, así que te invitamos a continuar practicando y dando lo mejor de ti. ¡Tus esfuerzos darán resultado!

Para abordar el área de Razonamiento Matemático presente en el examen del IPN, hemos diseñado esta guía en la que resolvemos 50 ejercicios que te ayudarán a prepararte.
Ahora bien, para presentarte este material, hemos segmentado esta guía de ejercicios en cinco post. En esta oportunidad, podrás ver los reactivos del 11 al 20 de la guía de Razonamiento Matemático. Ten en cuenta que para tener éxito en esta prueba, deberás prepararte en matemáticas y las demás áreas que componen el examen de admisión, así que toma nota y ¡Éxitos!
¿Qué viene en el examen del IPN?
Para que conozcas mejor cómo se compone el examen de admisión del Instituto Politécnico Nacional, empezamos por decirte que el mismo se compone de un total de 130 reactivos o preguntas. Estas se distribuyen en cinco áreas de conocimiento diferentes. La primera de ellas va enfocada a matemáticas y comunicación, mientras que la segunda, va orientada a Física, Química y Biología.
Ahora, para que tengas una idea de la ponderación e importancia de cada una de estas áreas en el examen, te mostramos un listado con la cantidad de preguntas de cada área:
- 50 preguntas de matemáticas.
- 40 preguntas de comunicación.
- 10 preguntas de biología.
- 15 preguntas de química.
- 15 preguntas de física.
Para no extendernos más, quedas invitado a resolver junto a nosotros la segunda parte de nuestra guía resuelta de ejercicios de Razonamiento Matemático del IPN:
Reactivo 11: Término general de una sucesión
Relacionar la sucesión con el término general que le corresponda.

- 1C, 2A, 3D, 4B
- 1C, 2D, 3A, 4B
- 1D, 2B, 3A, 4C
- 1D, 2A, 3B, 4C
Solución:
Para asociar la sucesión con el término general correspondiente, analizaremos las sucesiones de la columna izquierda, determinando su término general para finalmente relacionarlo con alguna de las opciones en la columna derecha.
Primera sucesión
Esta primera es la más sencilla de todas. Ya que n crece en saltos enteros de 1 (1, 2, 3,…), esta primera sucesión se obtiene al multiplicar por dos cada uno de esos n enteros. Se concluye entonces que el término general es:
a_{n}=\{2 n\}
En base a las opciones de la columna derecha, el término general para la sucesión 1 es el C.
1C.
Segunda sucesión
El término general de esta sucesión podemos extraerlo fácilmente al compararla con la sucesión del inciso 1.
Si a cada uno de los términos de la sucesión anterior se le resta 1, obtenemos la sucesión del inciso 2.
b_{n}=a_{n}-1=\{2,4,6,8,10,12, \ldots\}-1
b_{n}=\{2-1,4-1,6-1,8-1,10-1,12-1, \ldots\}=\{1,3,5,7,9,11, \ldots\}
Ya que el término general de la sucesión del inciso 1 es 2 n , el de esta sucesión será 2 n restado 1.
b_{n}=\{2 n-1\}
Comparando con las opciones de la columna derecha, el resultado corresponde con el de la opción A. Por tanto:
2A.
Tercera sucesión
Para este caso, debemos analizar por partes a los términos de la sucesión. En primer lugar, el signo negativo puede asociarse con el 1 en el numerador:
c_{n}=\left\{1,-\frac{1}{3}, \frac{1}{5},-\frac{1}{7}, \frac{1}{9},-\frac{1}{11}, \ldots\right\}=\left\{1, \frac{-1}{3}, \frac{1}{5}, \frac{-1}{7}, \frac{1}{9}, \frac{-1}{11}, \ldots\right\}
Ese signo negativo alternado puede ser representado por un -1 elevado a una potencia de que entregue: 1 para posiciones impares y -1 para posiciones pares.
Con (-1)^{n} se obtiene -1 en posiciones impares y 1 en posiciones pares, para n=1,2,3 \ldots Si le restamos uno a en el exponente, se obtiene el comportamiento deseado:
(-1)^{n-1}
\begin{array}{l} n=1 \rightarrow(-1)^{1-1}=1 \\ n=2 \rightarrow(-1)^{2-1}=-1 \\ n=3 \rightarrow(-1)^{3-1}=1 \end{array}
\vdots
Concluimos entonces que en el numerador del término general debe ir (-1)^{n-1} . Para el denominador, debemos fijarnos el comportamiento que tienen los denominadores de los términos de la sucesión.
1,3,5,7,9,11, \ldots
Esto se parece a la sucesión del inciso 2, que tiene como término general a:
2 n-1
De esta manera, concluimos que el término general de la sucesión 3 es:
c_{n}=\left\{1,-\frac{1}{3}, \frac{1}{5},-\frac{1}{7}, \frac{1}{9},-\frac{1}{11}, \ldots\right\}=\left\{\frac{(-1)^{n-1}}{2 n-1}\right\}
Comparando con la columna derecha, la opción correcta sería la D.
3D.
Cuarta sucesión
En esta última, nos centraremos en los denominadores de los términos ya que en los numeradores solo hay unos.
d_{n}=\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \ldots\right\}
Los denominadores pueden ser expresados como potencias de 2:
\begin{array}{l} 2^{0}=1 \\ 2^{1}=2 \\ 2^{2}=4 \\ 2^{3}=8 \\ 2^{4}=16 \\ 2^{5}=32 \end{array}
\vdots
La solución sería 2 elevado a n-1 . Ya que n=1,2,3, \ldots para que comience desde cero es necesario restar 1. Por lo tanto:
d_{n}=\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \ldots\right\}=\left\{\frac{1}{2^{n-1}}\right\}
Concluimos entonces que:
4B.
Uniendo todas las soluciones queda:
1C, 2A, 3D, 4B.
Escogemos como respuesta final a la opción a).
Reactivo 12: Términos faltantes de una sucesión
Seleccionar el par de números que completan respectivamente la siguiente sucesión:
-\frac{1}{3}, \_\_\_\_,\frac{1}{3}, \frac{2}{3}, \_\_\_\_\_
- 0, 1
- 0, -1
- 2/3, 1/3
- -2/3, 1/3
Solución:
Ya que son 2 los términos faltantes en la sucesión, la única información que podemos extraer es el cómo incrementa el término siguiente respecto del anterior. Esto lo podemos determinar restando a \frac{2}{3} con \frac{1}{3} , debido a que ambos son términos consecutivos.
\frac{2}{3}-\frac{1}{3}=\frac{1}{3}
Es decir, los términos distan entre ellos una cantidad constante igual a 1/3. El segundo término se puede calcular como:
a_{2}=a_{1}+\frac{1}{3}=-\frac{1}{3}+\frac{1}{3}=0
De igual forma calculamos el quinto elemento.
a_{5}=a_{4}+\frac{1}{3}=\frac{2}{3}+\frac{1}{3}=\frac{3}{3}=1
Concluimos entonces que los términos faltantes en la sucesión son 0 y 1 respectivamente.
-\frac{1}{3}, 0, \frac{1}{3}, \frac{2}{3}, 1
Comparando con las opciones del problema, la correcta sería la a).
Reactivo 13: Sucesiones numéricas
¿Cuál es el quinto elemento de la siguiente lista de números?
\frac{\sqrt{3}}{2}, \sqrt{3}, \frac{3 \sqrt{3}}{2}, 2 \sqrt{3}, \ldots
- 3 \sqrt{3}
- \frac{3 \sqrt{3}}{4}
- \frac{5 \sqrt{3}}{2}
- \frac{5 \sqrt{3}}{4}
Solución:
Para encontrar el siguiente término de la sucesión, intentaremos restar elementos contiguos y determinar si distan una cantidad constante, la sucesión sería una progresión aritmética y el término faltante lo encontraríamos sumando este incremento a 2 \sqrt{3} .
\sqrt{3}-\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}
\frac{3 \sqrt{3}}{2}-\sqrt{3}=\frac{\sqrt{3}}{2}
2 \sqrt{3}-\frac{3 \sqrt{3}}{2}=\frac{\sqrt{3}}{2}
La diferencia entre términos contiguos es constante y vale \frac{\sqrt{3}}{2} . El término a_{5} se determina como:
a_{5}=2 \sqrt{3}+\frac{\sqrt{3}}{2}=\frac{5 \sqrt{3}}{2}
Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 14: Series espaciales
¿Cuál de las siguientes figuras completa la serie?
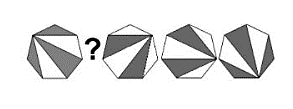
Solución:
Para resolver series gráficas o espaciales, debemos identificar un patrón de cambio en las figuras de la serie. Normalmente son rotaciones, traslaciones, adición o sustracción de elementos, cambios cromáticos o una combinación de dos o más de ellos.
Aunque existan parentescos entre problemas, lo mejor es tratar cada uno como un problema diferente y analizarlo a detalle.
En este caso, tenemos una figura que gira a medida que se desarrolla la serie. Debemos identificar cuánto rota una figura respecto a la anterior y si se mantiene constante a lo largo de la serie.
La magnitud de rotación, se puede determinar comparando 3 con 4 y 4 con 5. En la figura 3, el vértice al que llegan las líneas cambia al vértice inmediato en sentido horario en la figura 4.
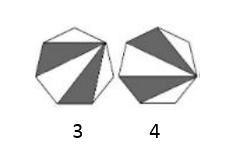
Lo mismo sucede entre las figuras 4 y 5. La rotación se da en sentido horario al vértice inmediato.
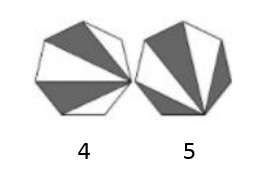
La rotación es en magnitud constante y siempre en sentido horario. Otra característica que podemos identificar, es que 3 y 4 solo tienen 2 franjas grises, mientras que 1 y 5 tienen 3. Podemos inferir que 2 debe tener 2 franjas grises.
En base a este análisis, la figura de la posición 2 debe tener el vértice en la esquina superior de la figura y poseer dos franjas grises. Comparando con las opciones del problema, la respuesta correcta es la figura c).

Reactivo 15: Series espaciales
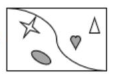
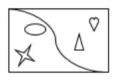
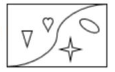
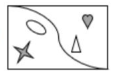
Encontrar la figura que sigue en la serie:

Solución:
Identifiquemos las transformaciones presentes en las figuras de la serie.
- El triángulo y el corazón presentan tres transformaciones. La dirección de sus puntas y el color cambia de forma alternada. Su posición en el recuadro cambia cada dos figuras, en 1 y 2 a la izquierda, en 3 a la derecha y por ende también en la cuarta
- La “s” entre dos esquinas en los recuadros cambia de forma alternada
- La estrella y la elipse tienen 3 transformaciones. Cada dos recuadros cambian de lugar con el corazón y el triángulo. Entre imágenes contiguas se encuentran rotados. Luego de rotar, vuelven a alinearse verticalmente pero cambiando de lugar
En base a todo este análisis, la siguiente figura debe tener:
- Al triángulo y al corazón en la zona derecha, blanco y gris, y apuntando hacia arriba y abajo respectivamente
- La “s” debe estar entre la esquina superior izquierda y la inferior derecha
- La estrella y la elipse deben estar en la zona izquierda, en la misma posición que en la figura anterior pero rotadas en sentido horario
Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 16: Arreglos gráficos
Determinar el elemento faltante en el siguiente arreglo:
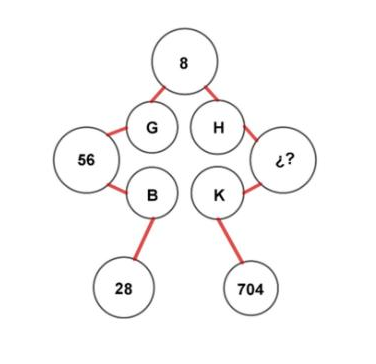
- 56
- 64
- 240
- 480
Solución:
En este problema, debemos identificar los números asociados a cada letra y las operaciones que se realizan entre ellos para obtener el resultado final. Según el abecedario la G se encuentra de séptima, la B de segunda, la H de octava y la K de decimoprimera.
G=7, B=2, H=8, K=11
Sustituyéndolas en la figura tenemos:
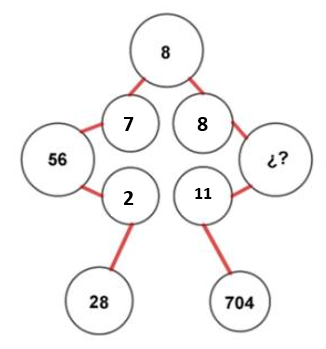
Ahora, debemos identificar qué operaciones se realizan para llegar a 28 de un lado y 704 de otro. Como el lado izquierdo está completo, empecemos por ahí. El tercer círculo tiene un 56 que puede expresarse como 8 \cdot 7=56 . Luego, el 56 se conecta con 2 para dar como resultado 28, si dividimos 56 con 2 el resultado es 28.
Siguiendo esta lógica, de lado derecho el círculo sin resultado debe ser 64, ya que 8 \cdot 8=64 . Si dividimos 64 entre 11 no se obtiene 704, pero si multiplicamos 64 \cdot 11 el resultado es 704. Concluimos entonces que el número faltante es 64.
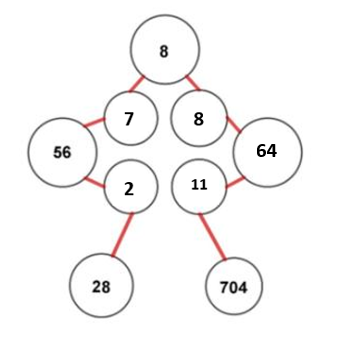
Comparando con las opciones del problema, la respuesta correcta es la b).
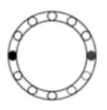
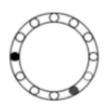
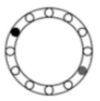
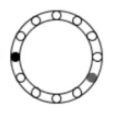
Reactivo 17: Secuencias gráficas
Determinar la figura siguiente de la secuencia.
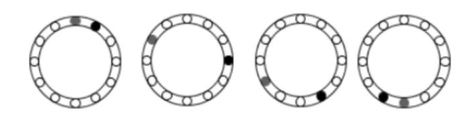
Solución:
En esta secuencia, tanto el punto gris como el negro cambian de posición en la periferia del anillo alternándose entre los circulo vacíos. Lo que debemos conocer para determinar la siguiente figura es: cuantas posiciones cambia cada uno y en qué sentido lo hace.
En las 4 figuras, tanto el punto gris como el negro se mueven 2 posiciones. El gris lo hace en sentido anti horario y el negro en sentido horario. Enumeremos las posiciones para facilitar la explicación.
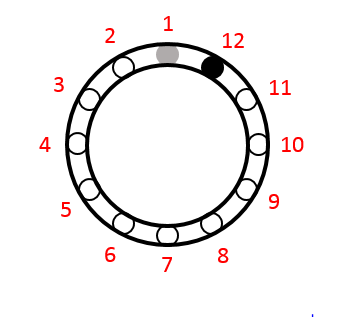
Ya que en la figura 4 el círculo gris está en la posición 7 y el negro en la 6, basados en nuestro análisis el gris debe moverse a la posición 9 y el negó a la posición 4.
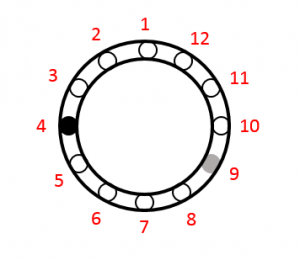
Comparando con las figuras en los incisos del problema, la respuesta correcta es la d).
Reactivo 18: Secuencias gráficas
Identificar la figura que corresponde al espacio vacío.
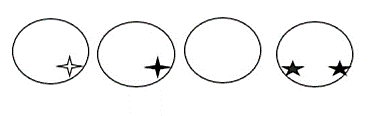
Solución:
Para encontrar la figura correcta, debemos pensar en los dibujos de la zona inferior como un solo objeto, es decir la estrella de 4 vértices como un solo objeto que cambia de blanco a negro y las dos estrellas de 5 vértices, juntas como un mismo objeto.
Ya que en la figura de la posición 4 tiene a las estrellas en color negro, la figura que la antecede debe tener dos estrellas de 5 vértices blancas. Si observamos las opciones del problema, la respuesta correcta sería la d).
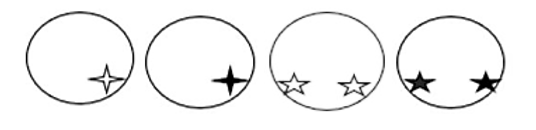
Reactivo 19: Secuencias gráficas
De acuerdo con los tres primeros términos de la sucesión, calcular el número de cuadrados negros necesarios para formar las primeras cuatro figuras de la secuencia.
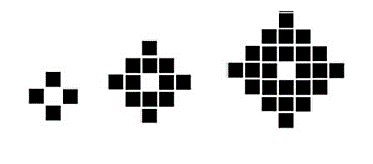
- 72
- 76
- 80
- 84
Solución:
Para encontrar la respuesta correcta, primero debemos comprender lo que solicita el problema. No se nos pide el número de cuadrados negros del siguiente término, sino la suma de cuadrados negros para formar los 4 primeros términos.
Primero, identifiquemos la ley que incrementa el número de cuadrados para el siguiente término.

Primer término, 4×4 y 4 cuadrados negros.

Segundo termino, 5×5 y 12 cuadrados negros.

Tercer término, 7×7 y 24 cuadrados negros.
En base al crecimiento impar en los cuadrados de cada figura, el siguiente debe ser 9×9. El número de cuadrados rellenos debemos extraerlo de la sucesión 4, 12, 24.
Lo primero que identificamos es que todos los números pueden expresarse como el anterior sumado con otra cantidad.
4=4
4+8=12
12+12=24
Los números por los que se suma el anterior para obtener el siguiente incrementa de 4 en 4, por lo tanto:
24+16=40
La siguiente figura debe ser de 9×9 con 40 cuadrados negros. Otra forma de expresar la secuencia de cuadrados negros es:
4(1)=4
4(3)=12
4(6)=24
4(10)=40
Donde 1, 3, 6, 10,… corresponde a una secuencia de números triangulares de la forma \frac{n(n+1)}{2} . Es decir 4 \cdot \frac{n(n+1)}{2}=2 n(n+1) . Volviendo a la pregunta del problema, la suma de cuadrados negros para los 4 primeros términos es:
N^{\circ} \text { cuadrados }=4+12+24+40=80
Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 20: Secuencias gráficas
Determinar el número de cuadrados que aparecerán en la figura número 8.
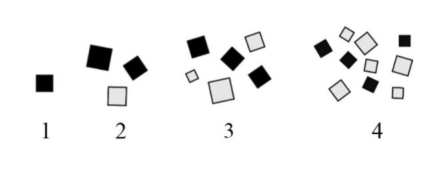
- 25
- 36
- 46
- 56
Solución:
Comencemos por comprender la solicitud del problema, no es necesario conocer cuántos cuadrados de un color y otro aparecen en la figura, sino el total de cuadrados. De la secuencia gráfica sabemos que:
\text { Figura } 1 \rightarrow 1 \text { Cuadrado }
\text { Figura } 2 \rightarrow 3 \text { Cuadrados }
\text { Figura } 3 \rightarrow 6 \text { Cuadrados }
\text { Figura } 4 \rightarrow 10 \text { Cuadrados }
De lo anterior, podemos identificar que si multiplicamos la posición actual n por la siguiente n+1 y la dividimos por 2, encontramos el valor del término actual:
a_{n}=\left\{\frac{n(n+1)}{2}\right\}
Comprobamos sustituyendo valores para n .
a_{1}=\left\{\frac{1(1+1)}{2}\right\}=\{1\}
a_{2}=\left\{\frac{2(2+1)}{2}\right\}=\{3\}
a_{3}=\left\{\frac{3(3+1)}{2}\right\}=\{6\}
a_{4}=\left\{\frac{4(4+1)}{2}\right\}=\{10\}
Podemos entonces determinar el número de cuadrados en la figura 8 al sustituir n=8 en el término general.
a_{8}=\left\{\frac{8(8+1)}{2}\right\}=\{36\}
La figura de la posición 8 tendrá un total de 36 cuadrados. Comparando este resultado con las opiniones del problema, indicamos como correcta a la b).