Guía IPN 2023 Pensamiento Matemático | 40 ejercicios resueltos

¿Quieres aprender cómo se resuelven los 40 reactivos de pensamiento matemático de la guía IPN? ¿Sí?, entonces llegaste al lugar correcto.

En este tutorial vamos a resolver todos los ejercicios correspondientes a la materia de pensamiento matemático de cara al nuevo examen de admisión al poderosísimo Instituto Politécnico nacional.

Vamos a resolver los 40 reactivos en 4 partes, en esta primera parte nos enfocaremos en explicar pasa a paso del reactivo 1 al 10.

El siguiente es un resumen general sobre el ingreso al IPN:

• Carreras ofertadas en IPN: 70+.
• Porcentaje de Aceptación: 20%.
• Preguntas en el examen de Admisión: 140 preguntas.
• Nuevos temas: historia e inglés (reading comprehension).
• Tipo: selección múltiple.

Si es la primera vez que presentas el examen debes saber que su estructura es nueva, por lo que es muy importante que te asegures de estudiar los temas correspondientes al proceso de selección.

Estructura del Examen IPN

La estructura del examen al IPN ha cambiado respecto a los años previos. Ahora, el número de reactivos por asignatura varía según el área de conocimientos de tu carrera. Las carreras en el Politécnico Nacional se dividen en 3 áreas:

• Ingeniería y Ciencias Físico Matemáticas IyCFM
• Ciencias Sociales y Administrativas CSA
• Ciencias Médico Biológias CMB

La siguiente tabla muestra la estructura de reactivos por materia para cada área.

Materia	IyCFM	CMB	CSyA
Matemáticas	37	33	35
Competencia escrita	20	20	25
Competencia lectora	20	20	20
Reading comprehension	10	10	10
Historia	10	10	20
Biología	9	17	10
Química	17	17	10
Física	17	13	10

Estructura del nuevo examen de ingreso al instituto Politécnico Nacional 2024.

¿Qué tan difícil es el examen al IPN?

Todo aspirante al Politécnico Nacional se ha hecho la pregunta: ¿es difícil la prueba para entrar al IPN? Aunque no lo creas, la respuesta depende de ti.

Para la convocatoria de este año se han agregado 2 asignaturas nuevas y la estructura ha cambiado. En la materia de pensamiento matemático (antes razonamiento matemático) los reactivos tienen una complejidad similar a los años anteriores.

Sin embargo, la complejidad radica en la cantidad de subtemas que debes dominar, ya que en tu examen no se sabe si van a aparecer todos ellos, por lo que debes asegurarte de dominarlos en su totalidad.

Temario pensamiento matemático IPN

Estos son los temas de pensamiento matemático que deberás dominar antes de presentar el examen de ingreso:

• Secuencias
  • Sucesiones numéricas
  • Secuencias alfanuméricas
  • Expresiones generales
• Geometría espacial
  • Secuencias con patrones geométricos
  • Operaciones de simetría
  • Perspectivas cortes y figuras
• Mediciones
  • Medidas de figuras y objetos
• Análisis de datos
  • Conjunto de datos y análisis de información
• Pensamiento analítico
  • Resolución de problemas

¿Cómo resolver la guía del IPN?

Antes de iniciar con la solución de los reactivos:

• Te recomiendo examinar la bibliografía recomendada por la guía del IPN.
• Estudia el temario y comprende los fundamentos para que sencillo identificar los temas de mayor complejidad.

Un error común entre los aspirantes consiste en estudiar los temas mientras resuelven la guía. Estudiando de esta forma pierdes tiempo y vas a ciegas sin una metodología óptima a la hora de estudiar.

Recomendaciones:

Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo y así obtener los aciertos necesarios para quedar en tu carrera.

• Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
• Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
• Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
• Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
• Te advierto que la guía del IPN tiene algunos errores, aquí te señalamos cuáles son.

Reactivo 1

Identificar los tres elementos que falta en la sucesión aritmética:

\frac{5}{2}, 4,\frac{11}{2}, 7, ___,___,___, 13, \dots 

1. \frac{13}{2}, 10,\frac{21}{2}
2. \frac{17}{2}, 10,\frac{23}{2}
3. \frac{13}{2}, 11,\frac{21}{2}
4. \frac{17}{2}, 11,\frac{23}{2}

Solución:

En este caso, no es necesario comprobar el tipo de sucesión que representan los números, porque el enunciado establece que se trata de una sucesión aritmética.

Podemos resolver el problema mediante dos enfoques: sumando la diferencia desde el 7 o encontrando el término general de la sucesión. De cara al examen, la opción más rápida es la primera. Calculamos la diferencia restando términos contiguos.

d=7-\frac{11}{2}=\frac{14-11}{2}=\frac{3}{2}

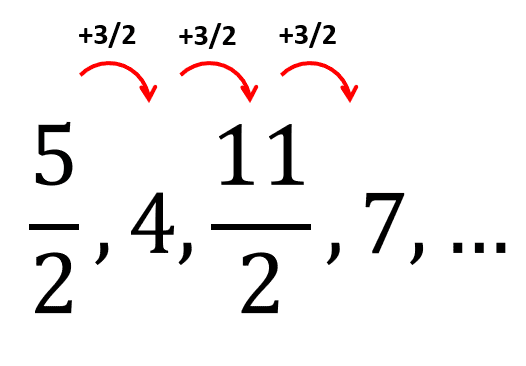
De esta forma, los siguientes 3 elementos son:

{a}_{5}=7+\frac{3}{2}=\frac{17}{2}

{a}_{6}=\frac{17}{2}+\frac{3}{2}=10

{a}_{7}=10+\frac{3}{2}=\frac{23}{2}

Finalmente:

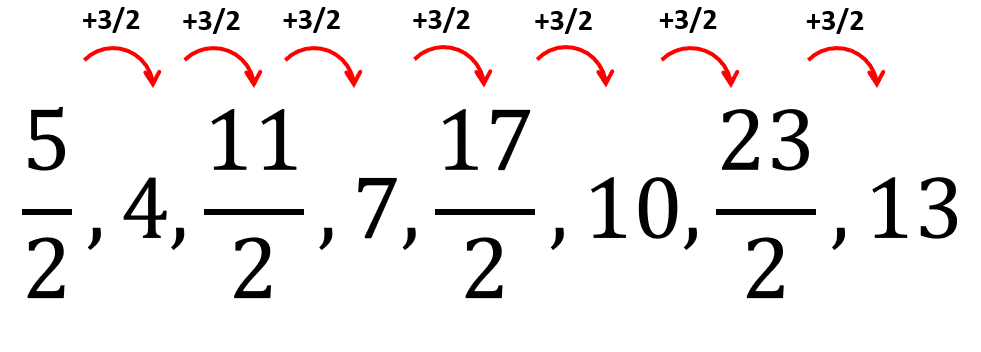
Términos restantes: \frac{17}{2}, 10,\frac{23}{2} .

Comparando con los incisos, concluimos que la respuesta correcta está en b).

Reactivo 2

Identificar los tres elementos que faltan en la siguiente sucesión:

-20, -19, -17, -13, ___,___,___, 107, 235,\dots 

1. -5, 11, 43
2. -3, 15, 32
3. -5, 15, 73
4. -3, 11, 71

Solución:

Iniciamos identificando el tipo de sucesión o ley de cambio entre los términos de la sucesión. Restamos términos semejantes para identificar la distancia entre ellos.

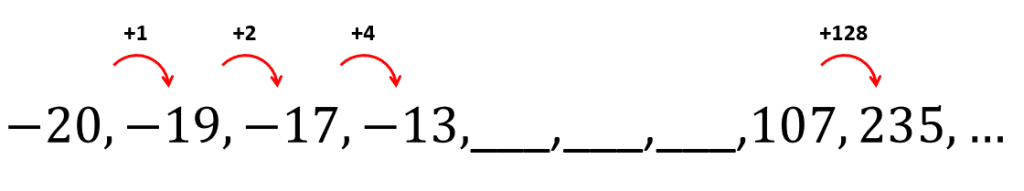
En este caso, la diferencia no es constante. Analizando cómo evolucionan las diferencias, podemos notar que todas pueden expresarse como potencias de base 2.

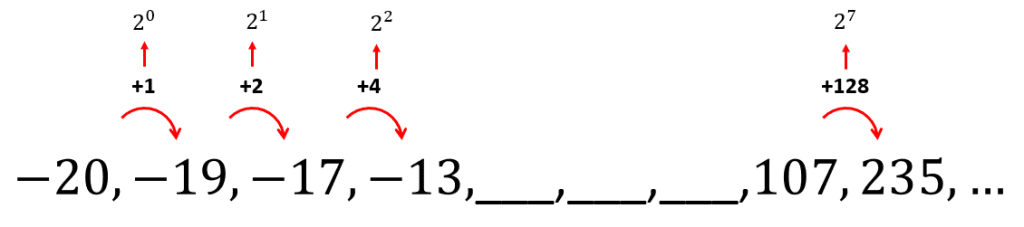
Teniendo esto en cuenta lo anterior, las diferencias para los términos desconocidos son:

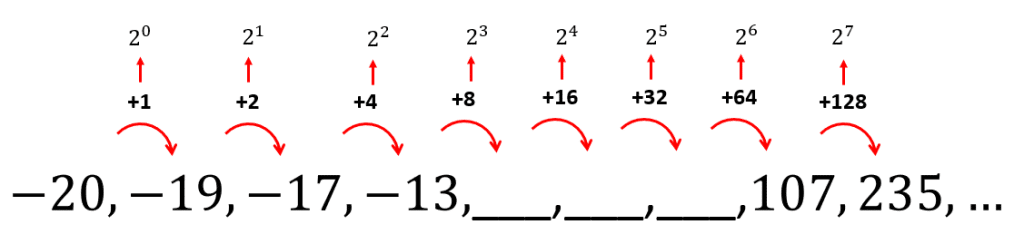
Finalmente, los términos restantes quedarían como:

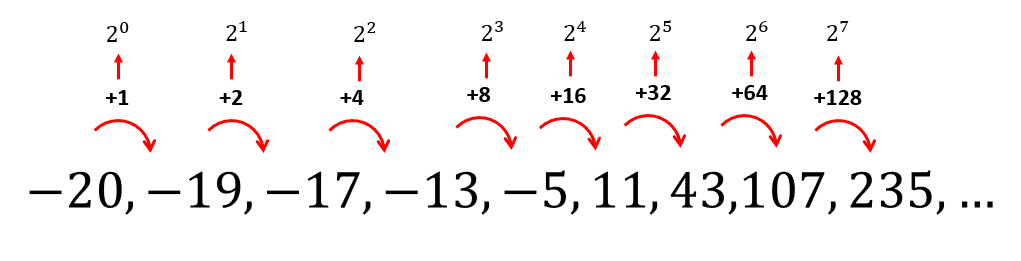
El inciso que contiene a los términos: -5, 11 y 43 es el a). Un truco de examen, es que pudimos encontrar el primer término faltante: -5. Con este descartamos a los incisos b) y d). Nos queda calcular el segundo para concluir entre el a) y el c). De esta forma acortamos tiempo en la solución.

Reactivo 3

¿Qué números se ubican en las posiciones 12 y 16 de la sucesión que se muestra enseguida?

3, 7, 11, 15, \dots 

1. 39 y 57
2. 47 y 63
3. 45 y 71
4. 37 y 73

Solución:

Iniciamos calculando la diferencia entre términos sucesivos.

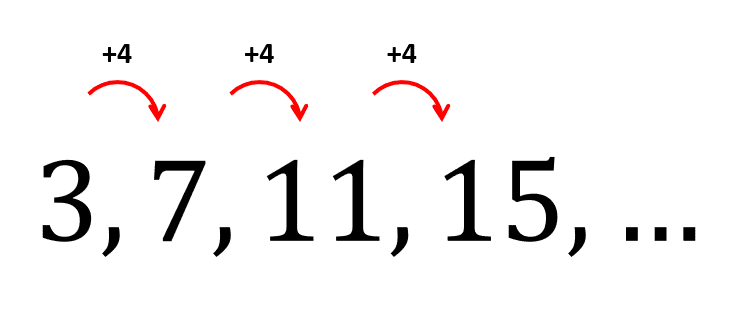
Debido a que la diferencia es constante, concluimos que se trata de una sucesión aritmética. Ahora, encontrar los términos 12 y 16 sumando sucesivamente tomará más tiempo que si utilizamos la fórmula del término general.

{a}_{n}={a}_{1}+d\left(n-1\right), n\ge 1

De la sucesión en el enunciado extraemos al término en la posición 1: {a}_{1}=3 . Sustituimos.

{a}_{n}=3+4\left(n-1\right)

Sustituimos n=12  y n=16

{a}_{12}=3+4\left(12-1\right)=47

{a}_{16}=3+4\left(16-1\right)=63

Los términos {a}_{12} y {a}_{16} de la sucesión aritmética son: 47 y 63 respectivamente.

La respuesta correcta es el inciso b).

Reactivo 4

Identificar los dos términos que continúan la secuencia:

\frac{\pi }{3}, \frac{5\pi }{6}, \frac{4\pi }{3}, \frac{11\pi }{6}, \frac{7\pi }{3}, \dots 

1. \frac{17\pi }{6} , \frac{9\pi }{3}  
2. \frac{15\pi }{6} , \frac{9\pi }{3}  
3. \frac{15\pi }{6} , \frac{10\pi }{3}  
4. \frac{17\pi }{6} , \frac{10\pi }{3}  

Solución:

Aunque parezca intimidante ver que todos los términos tienen a \pi  en el numerador, lo cierto es que podemos resolver la sucesión prescindiendo de este, debido a que todos son fracciones de \pi  . Solo nos interesan las fracciones. Otra forma de verlo, es que podemos extraer a \pi  como factor común.

\frac{\pi }{3},\mathrm{ }\frac{5\pi }{6},\mathrm{ }\frac{4\pi }{3},\mathrm{ }\frac{11\pi }{6},\mathrm{ }\frac{7\pi }{3},\mathrm{ }\dots \mathrm{ }\equiv \frac{1}{3},\mathrm{ }\frac{5}{6},\mathrm{ }\frac{4}{3},\mathrm{ }\frac{11}{6},\mathrm{ }\frac{7}{3},\mathrm{ }\dots 

Ahora, calculamos la diferencia entre términos consecutivos.

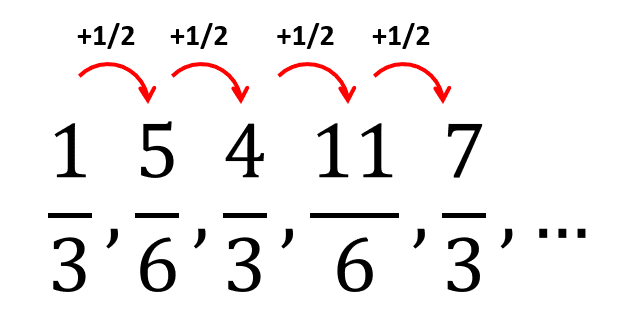
Encontramos los dos siguientes términos sumando 1/2 a \frac{7}{3} de forma sucesiva.

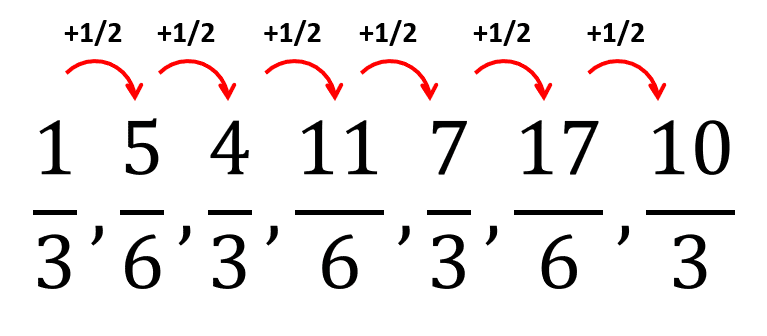
Multiplicamos a todos los términos por \pi  para regresar a la sucesión original.

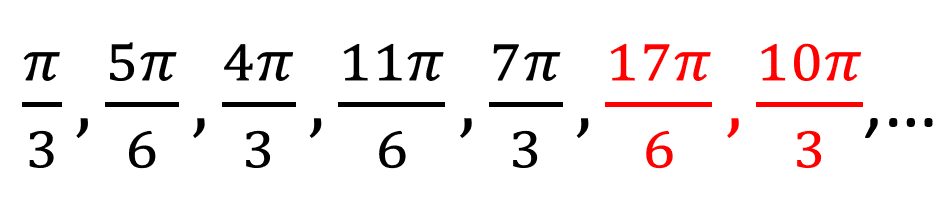
Examinando los incisos, concluimos que la respuesta correcta es d).

Reactivo 5

Identificar la expresión que reproduce la sucesión siguiente:

-1, -\frac{1}{2}, 2, -\frac{7}{2}, 5, -\frac{13}{2}, \dots 

1. 2n-1
2. \frac{2n-1}{2}
3. \left(\frac{1}{2}n-1\right)
4. (-1{)}^{n}\left(\frac{3}{2}n-1\right)

Solución:

Examinando los términos de la sucesión, vemos que siguen un patrón alternado de signos: +, -, +, -, … Esto solo se logra adicionando al término de la sucesión un factor del tipo {\left(-1\right)}^{n} o {\left(-1\right)}^{n+1} . Teniendo esto en cuenta, el único inciso que posee dicho factor es el d).

(-1{)}^{n}\left(\frac{3}{2}n-1\right)

Comprobamos sustituyendo a n\ge 0 .

{a}_{0}=(-1{)}^{0}\left[\frac{3}{2}\left(0\right)-1\right]=\left(1\right)\left(-1\right)=-1

{a}_{1}=(-1{)}^{1}\left[\frac{3}{2}\left(1\right)-1\right]=\left(-1\right)\left(\frac{1}{2}\right)=-\frac{1}{2}

{a}_{2}=(-1{)}^{2}\left[\frac{3}{2}\left(2\right)-1\right]=\left(1\right)\left(2\right)=2

⋮

Concluimos el problema indicando como respuesta correcta al inciso d).

Reactivo 6

Identificar la sucesión aritmética dada por la expresión \frac{2n}{2n+1} , que toma los valores n=1, 2, 3, \dots 

1. \frac{2}{3},\frac{3}{7},\frac{6}{7},\frac{8}{9},\dots
2. \frac{2}{3},\frac{4}{5},\frac{6}{7},\frac{8}{9},\dots
3. \frac{3}{7},\frac{5}{5},\frac{6}{7},\frac{8}{9},\dots
4. -\frac{2}{3},\frac{4}{5},-1,\frac{8}{9},\dots

Solución:

Vamos a ir sustituyendo los valores de n en la expresión y a medida que obtengamos los términos de la sucesión, iremos descartando los incisos del enunciado.

Sustituimos n=1 .

{a}_{1}=\frac{2\left(1\right)}{2\left(1\right)+1}=\frac{2}{3}

Descartamos los incisos c y d. Nos queda decidir entre el a y el b.

Sustituimos n=2 .

{a}_{1}=\frac{2\left(2\right)}{2\left(2\right)+1}=\frac{4}{5}

El inciso a tiene como segundo término a \frac{3}{7} . Concluimos entonces que la respuesta correcta es el inciso b).

Reactivo 7

Completar los dos elementos que faltan en la secuencia:

8163452, 6143258, _______, 2183654, ______, …

1. 4231865 – 8631542
2. 3426581 – 6421538
3. 4123856 – 8163452
4. 3512468 – 6428531

Solución:

Para completar los espacios vacíos, debemos analizar qué dígitos permanecen constantes entre términos, cuales cambian y la forma en que cambian. Lo primero que podemos notar, es que todos los números tienen la siguiente estructura:

Par – impar – par – impar – par – impar – par

Por otra parte, los impares permanecen constantes: 1, 3, y 5.

Los números pares cambian de la siguiente forma: se les restan 2 de forma sucesiva, cuando el número par llega hasta el 2, en lugar de llegar a cero se reinicia a 8.

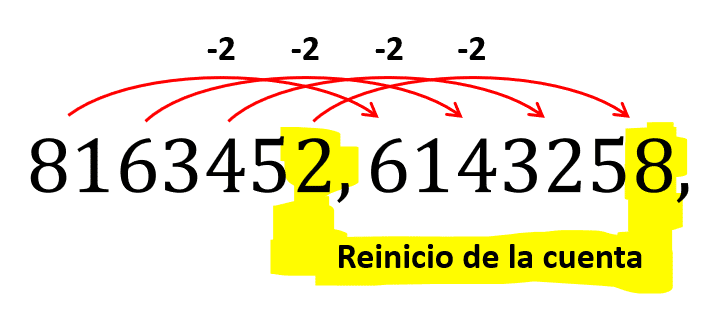
Siguiendo esta lógica, los términos faltantes quedarían:

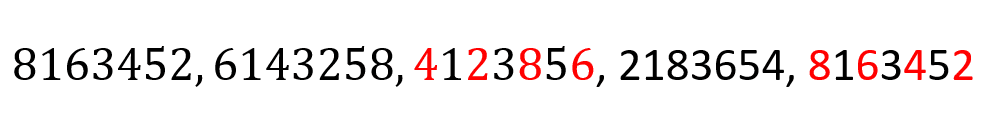
Concluimos indicando como respuesta correcta al inciso c).

Reactivo 8

Calcular el décimo quinto, décimo sexto y vigésimo primer término de una progresión aritmética que mantiene una diferencia de \frac{1}{5} entre cada elemento y donde la suma de los primeros 20 términos es igual a 198.

1. \frac{54}{5}, 11, 12
2. \frac{18}{5}, 5, 9
3. 42, 11,\frac{67}{5}
4. \frac{18}{5}, 5,\frac{49}{5}

Solución:

Este problema tiene muchos temas juntos: progresiones aritméticas, lenguaje natural/algebraico y suma de sucesiones numéricas. Iniciemos repasando el enunciado para extraer toda la información.

Calcular el décimo quinto, décimo sexto y vigésimo primer término de una progresión aritmética…

Los términos mencionados son: {a}_{15} , {a}_{16} y {a}_{21} . Por otra parte, las progresiones aritméticas son aquellas cuya diferencia entre términos contiguos es constante y se pueden generalizar mediante la siguiente expresión:

{a}_{n}={a}_{1}+d\left(n-1\right)

Donde {a}_{1} es el primer término, d es la diferencia y n=1, 2, 3, \dots  Del enunciado, sabemos que la diferencia d=\frac{1}{5} .

{a}_{n}={a}_{1}+\frac{1}{5}\left(n-1\right)

Ahora, la suma de los primeros 20 términos de una progresión aritmética se obtiene mediante la siguiente fórmula:

s=\frac{{a}_{1}+{a}_{n}}{2}\cdot n

En nuestro caso n=20 .

s=10\left({a}_{1}+{a}_{20}\right)

El término {a}_{20} se puede escribir como:

{a}_{20}={a}_{1}+d\left(20-1\right)={a}_{1}+\frac{19}{5}

Sustituimos.

s=198=10\left(2{a}_{1}+\frac{19}{5}\right)=20{a}_{1}+38

Despejamos al término {a}_{1} .

{a}_{1}=\frac{198-38}{20}=\frac{160}{20}=8

Sustituimos en la fórmula del término general.

{a}_{n}=8+\frac{1}{5}\left(n-1\right)

Solo nos queda sustituir los correspondientes valores de n .

{a}_{15}=8+\frac{1}{5}\left(15-1\right)=\frac{54}{5}

{a}_{16}=8+\frac{1}{5}\left(16-1\right)=11

{a}_{21}=8+\left(21-1\right)=12

Comparando con los incisos, indicamos como respuesta correcta al a). Originalmente la guía tiene un error de tipografía en el inciso a), en lugar de poner \frac{54}{5} indica \frac{42}{5} .

Reactivo 9

Relacionar cada sucesión con su tipo.

1. 1B, 2A, 3D, 4C
2. 1C, 2D, 3A, 4B
3. 1B, 2C, 3D, 4A
4. 1C, 2B, 3A, 4D

Solución:

Debemos analizar cada una de las sucesiones en la columna izquierda, para asociarla con la clasificación correspondiente en la columna derecha.

Primera sucesión.

32, 47, 62, 77, 92, …

La diferencia entre términos semejantes es constante.

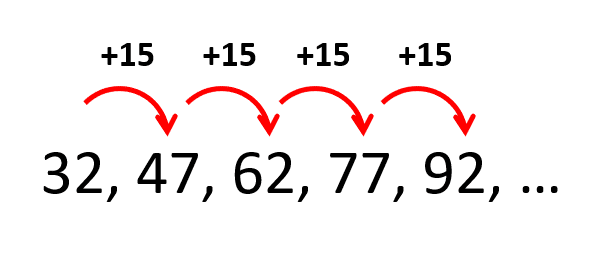
Es una sucesión aritmética ascendente, porque los términos incrementan a razón de 15: 1B. Descartamos a los incisos b) y d) porque inician con 1C. Vamos con la segunda sucesión.

61, 122, 244, 488, …

Debido a que los términos no disminuyen, la sucesión no puede ser descendente. Tampoco oscilante, porque no cambia el signo de los términos a medida que se desarrolla la sucesión. Por lógica, esta sucesión debe ser geométrica: 2C.

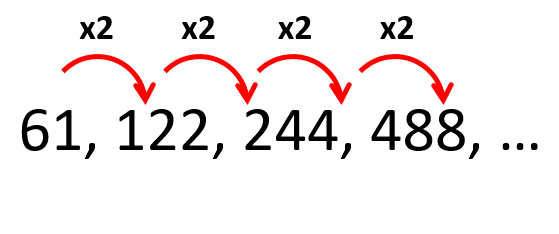
Con esta información: 1B, 2C, … podemos concluir que la respuesta correcta es el inciso c).

Reactivo 10

Elegir los términos que faltan en la siguiente sucesión:

\sqrt{3}{e}^{1},3, ____, ____, 9\sqrt{3}{e}^{-3},27{e}^{-4}

1. \sqrt{3}{e}^{-2},9{e}^{3}
2. 3\sqrt{3}{e}^{-1},9{e}^{-2}
3. 3{e}^{-1},3\sqrt{3}{e}^{-2}
4. 3\sqrt{3}{e}^{-2},9{e}^{3}

Solución:

Claramente esta no puede ser una sucesión aritmética, porque el principal cambio entre los términos ocurre en sus exponentes. Comprobamos que sea una sucesión geométrica, dividiendo términos consecutivos.

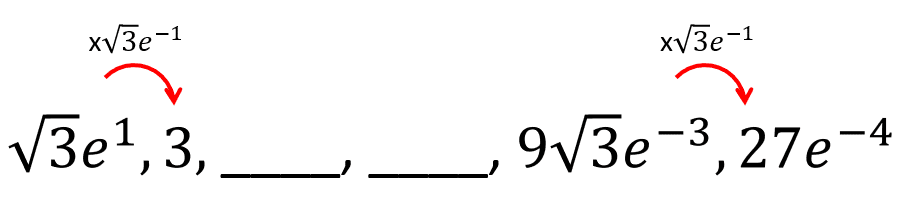
Multiplicamos al 3 por \sqrt{3}{e}^{-1} para encontrar el primer espacio vacío.

{a}_{3}=3\cdot \sqrt{3}{e}^{-1}=3\sqrt{3}{e}^{-1}

Con este resultado parcial, podemos concluir que la respuesta correcta es el inciso b) porque el resto inicia con valores distintos a 3\sqrt{3}{e}^{-1} . Si calculamos el siguiente término obtenemos:

{a}_{4}=\left(\sqrt{3}{e}^{-1}\right)\left(3\sqrt{3}{e}^{-1}\right)=9{e}^{-2}