¡Felicidades aspirante! Llegamos a la quinta y última parte de la guía de física para el área de IyCFM, como preparación al examen de ingreso del poderosísimo IPN.

Reactivo 41
Considerando que el vector de área y el campo magnético se dirigen hacia la misma dirección. ¿Cuál es el signo de la fuerza electromotriz inducida si el flujo es creciente y \frac{d\left({\theta }_{B}\right)}{dt} es positiva?
- neutro
- positivo
- negativo
- positivo – negativo
Solución:
La ley de inducción de Faraday-Lenz establece que la fuerza electromotriz inducida se opone a la variación de flujo magnético respecto del tiempo.
\epsilon =-\frac{d{\varphi }_{M}}{dt}
Por otra parte, el flujo magnético se calcula como el producto escalar entre el campo magnético y el vector área asociado a una superficie.
{\varphi }_{M}=\overrightarrow{B}\cdot \overrightarrow{S}=B\cdot S\cdot \mathrm{cos}\theta
Ya que el ángulo entre los vectores es cero porque apuntan en la misma dirección, el valor del flujo es positivo. Debido a que el flujo va en incremento, la variación del flujo respecto del tiempo es positiva.
Teniendo en cuenta que el valor de \frac{d{\varphi }_{M}}{dt} es positivo, multiplicado por el menos de la ley de Lenz hace que la FEM inducida tenga signo negativo. Concluimos que la respuesta correcta es el inciso c).
Reactivo 42
El parámetro que, dado un tren de ondas, indica la distancia entre dos puntos adyacentes que tienen la misma fase de la onda es:
- el periodo
- la amplitud
- la frecuencia
- la longitud de onda
Solución:
La longitud de onda \lambda es la distancia que existe entre dos crestas o valles consecutivos de una onda que se propaga en un medio.
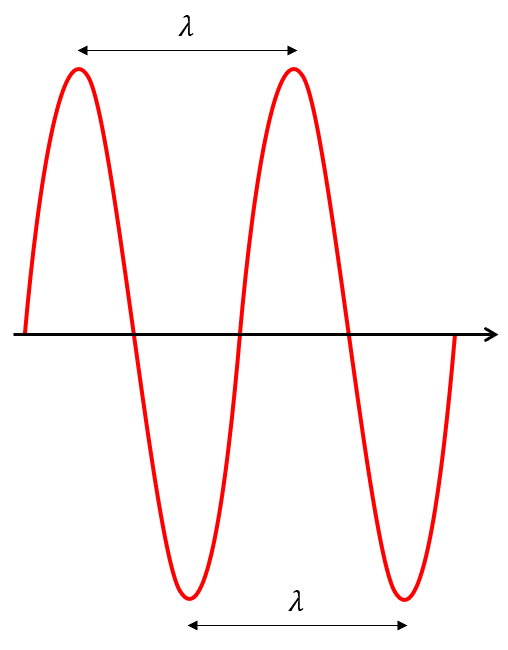
La respuesta correcta es el inciso d).
Reactivo 43
En una cuerda tensa se producen ondas con una frecuencia de 250 Hz a una velocidad de propagación de 160 m/s. ¿Cuál es la longitud de onda?
- \lambda =0.64\mathrm{m}
- \lambda =0.725\mathrm{m}
- \lambda =1.625\mathrm{m}
- \lambda =2.625\mathrm{m}
Solución:
Para resolver el problema, utilizamos la ecuación que relaciona la velocidad de propagación, la frecuencia y la longitud de onda.
v=\lambda \cdot f
Despejamos la longitud de onda.
\lambda =\frac{v}{f}
Sustituimos y calculamos.
\lambda =\frac{160}{250}=0.64 \mathrm{m}
La longitud de onda es igual a 0.64 metros.
La respuesta correcta es el inciso a).
Continúa practicando física para el área de IyCFM del IPN:
- Física reactivos del 1 al 10
- Física reactivos del 11 al 20
- Física reactivos del 21 al 30
- Física reactivos del 31 al 40
Reactivo 44
La ________ es un fenómeno característico de las magnitudes _________, caracterizado por su propagación “anómala” en las cercanías de un obstáculo o una abertura comparable en ______ a su longitud de onda.
- difracción – ondulatorias – contraposición
- difracción – ondulatorias – tamaño
- reflexión – ondulatorias – contraposición
- reflexión – oscilatorias – tamaño
Solución:
Examinando el enunciado, podemos discernir que la frase incompleta hace referencia a un fenómeno ondulatorio respecto a la anomalía que sufren las ondas cuando atraviesan aberturas cuyo tamaño es comparable con su longitud de onda.
La difracción es un fenómeno ondulatorio que se caracteriza por la desviación de la onda cuando ésta atraviesa una rendija muy pequeña y cuyo efecto es más notorio cuando la abertura es comparable con su longitud de onda.
Teniendo en cuenta esto y considerando los incisos, las palabras que completan correctamente la frase son: difracción, ondulatorias y tamaño.
La difracción es un fenómeno característico de las magnitudes ondulatorias, caracterizado por su propagación “anómala” en las cercanías de un obstáculo o una abertura comparable en tamaño a su longitud de onda.
La respuesta correcta es el inciso b).
Reactivo 45
Relacionar cada concepto con su significado.

- 1D, 2A, 3B
- 1A, 2C, 3D
- 1D, 2B, 3A
- 1A, 2D, 3C
Solución:
Vamos a definir brevemente cada uno de los términos que se encuentran en la columna izquierda, para luego relacionarlos correctamente con los conceptos de la columna derecha.
Reflexión.
Es un fenómeno ondulatorio, donde un rayo que se propaga a través de un primer medio incide sobre la superficie de otro. Parte del rayo incidente rebota en la superficie y se refleja en el primer medio.
Examinando la tabla, indicamos: 1D. Descartamos los incisos b y d.
Refracción.
Es un fenómeno ondulatorio, donde un rayo que se propaga a través de un primer medio incide sobre la superficie de otro. Parte del rayo incidente atraviesa la superficie y se propaga por el segundo medio.
Para este caso: 2A. Con esta información: 1D, 2A, … Podemos concluir que la respuesta correcta es el inciso a).
Reactivo 46
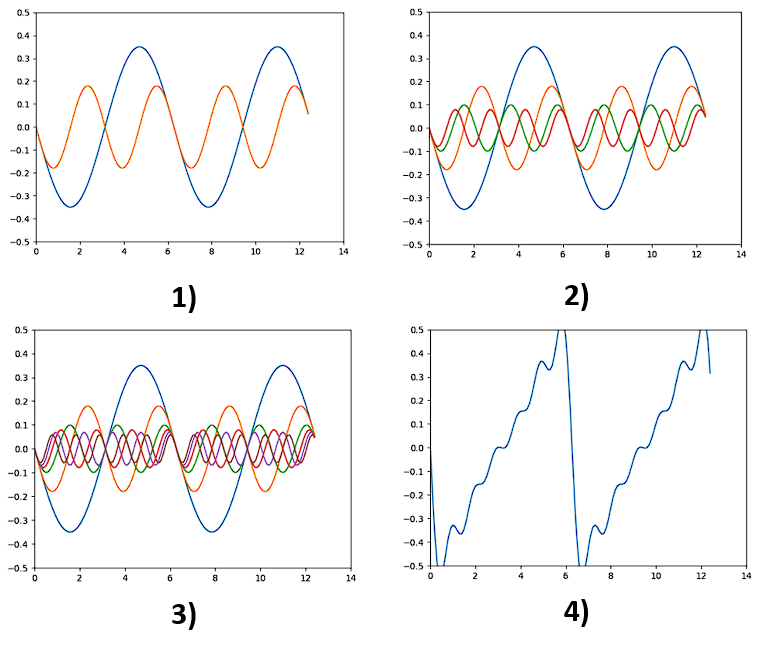
En las siguientes imágenes se muestra un ejemplo de _________ de onda.
- Reflexión
- Difracción
- Interferencia
- Superposición
Solución:
En la figura del enunciado se ven 4 gráficas, en las que aumenta de forma progresiva la cantidad de señales sinusoidales.
En el cuarto gráfico, se puede ver una señal con forma triangular, la cual se construye a partir de la suma de todas las señales sinusoidales que se adjuntan hasta la figura 3). Esto es posible gracias al principio de superposición.
La superposición es un fenómeno ondulatorio, en el que dos o más señales que se encuentran en un punto del espacio se suman para dar una señal resultante. En este caso, la señal resultante es la que se muestra en la figura 4).
Examinando los incisos, concluimos que la respuesta correcta es el d).
Como dato extra, la superposición y la descomposición espectral de funciones, comprenden las bases de las telecomunicaciones, el estudio de señales, el análisis de sistemas y el control de procesos. Siendo la transformada de Laplace, de Fourier y la transformada Z las aplicaciones matemáticas directas sobre la superposición de ondas.
Reactivo 47
Relacionar cada sonido con el valor que le corresponde de su nivel de intensidad sonora en decibel (dB) usando la expresión 10\mathrm{l}\mathrm{o}\mathrm{g}\left(B\right) . Donde B={10}^{2} equivale a un murmullo; B={10}^{6} , a una conversación normal y B={10}^{9} , a un martillo perforador. El nivel de intensidad sonora de la onda de sonido está a una distancia de 1 m desde la fuente en cada uno de los ejemplos mencionados.

- 1A, 2D, 3B
- 1B, 2A, 3C
- 1A, 2B, 3D
- 1B, 2C, 3A
Solución:
Para relacionar correctamente el sonido con su nivel en decibelios, debemos realizar el cálculo a partir de los datos suministrados por el enunciado. Comencemos con el murmullo.
Murmullo.
\mathrm{d}\mathrm{B}=10\mathrm{log}\left({10}^{2}\right)=2\cdot 10\mathrm{log}\left(10\right)
El logaritmo base 10 de 10 es 1.
\mathrm{d}\mathrm{B}=2\cdot 10\mathrm{log}\left(10\right)=2\cdot 10\left(1\right)
\mathrm{d}\mathrm{B}=20
Para el murmullo: 1B. Descartamos los incisos a y c.
Conversación normal.
\mathrm{d}\mathrm{B}=10\mathrm{log}\left({10}^{6}\right)=6\cdot 10\mathrm{log}\left(10\right)
\mathrm{d}\mathrm{B}=60
Para la conversación normal: 2A. Con esta información: 1B, 2A, … podemos concluir que la respuesta correcta es el inciso b).
Reactivo 48
La rama de la Física que se relaciona con el estudio de las formas de onda de algunos instrumentos como la flauta, el clarinete y la trompeta es la:
- estática
- acústica
- hidráulica
- termodinámica
Solución:
El estudio de las ondas sonoras desde el aspecto físico y la formulación de modelos matemáticos, le corresponde a la acústica física. Es una rama de la física que estudia los fenómenos ondulatorios que se propagan a través de medios materiales debido a cambios de presión.
La acústica, estudia el sonido desde numerosos enfoques, incluyendo las implicaciones físicas. Algunas subramas de la acústica son: la psicoacústica, la música, la fonética, la acústica estructural, entre otras. Teniendo esta definición en cuenta y considerando a los incisos, concluimos que la respuesta correcta se encuentra en el b).
Reactivo 49
¿Cuál es la intensidad del sonido en un cuarto cuyo nivel medido es de 85 dB? Considerar {I}_{0}=1\times {10}^{-12}\mathrm{W}/{\mathrm{m}}^{2} .
- 1.6\times {10}^{5}\mathrm{W}/{\mathrm{m}}^{2}
- 2.5\times {10}^{-4}\mathrm{W}/{\mathrm{m}}^{2}
- 3.16\times {10}^{-4}\mathrm{W}/{\mathrm{m}}^{2}
- 3.16\times {10}^{-8}\mathrm{W}/{\mathrm{m}}^{2}
Solución:
La intensidad sonora, es una magnitud que permite estimar la potencia por metro cuadrado, producida por una fuente sonora y medida en algún punto del espacio. Al igual que el nivel de presión sonora NPS, la intensidad sonora puede ser expresada en decibelios.
La expresión para calcular los dB de IS es:
{\mathrm{d}\mathrm{B}}_{\mathrm{I}\mathrm{S}}=10\mathrm{log}\frac{I}{{I}_{o}}
Donde {I}_{o} es el umbral de audición igual a 1\times {10}^{-12}\mathrm{W}/{\mathrm{m}}^{2} . Tenemos el valor de los decibelios y a {I}_{o} , podemos despejar a I de la ecuación.
{\mathrm{d}\mathrm{B}}_{\mathrm{I}\mathrm{S}}=10\mathrm{log}\frac{I}{{I}_{o}}\to \mathrm{log}\frac{I}{{I}_{o}}=\frac{{\mathrm{d}\mathrm{B}}_{\mathrm{I}\mathrm{S}}}{10}
Aplicamos la base 10 en ambos miembros de la igualdad.
\frac{I}{{I}_{o}}={10}^{\frac{{\mathrm{d}\mathrm{B}}_{\mathrm{I}\mathrm{S}}}{10}}\to I={I}_{o}\cdot {10}^{\frac{{\mathrm{d}\mathrm{B}}_{\mathrm{I}\mathrm{S}}}{10}}
Sustituimos y resolvemos.
I=1\times {10}^{-12}\cdot {10}^{\frac{85}{10}}=1\times {10}^{-12}\cdot {10}^{8.5}
I=1\times {10}^{-12}\cdot {10}^{8}\cdot {10}^{0.5}=3.16\times {10}^{-4}\mathrm{W}/{\mathrm{m}}^{2}
La intensidad sonora es de 3.16\times {10}^{-4} Watts por metro cuadrado.
Seleccionamos como respuesta correcta al inciso c).
Reactivo 50
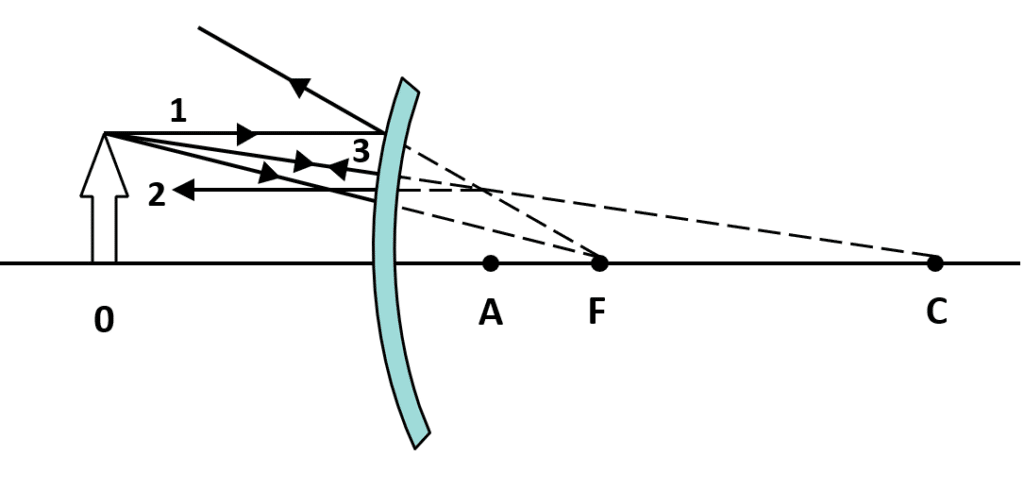
En la imagen se muestra una lente convergente, la cual describe el trazo de rayos 1, 2, y 3 para encontrar la posición de la imagen del objeto colocado en el punto O. ¿En qué punto se encuentra la posición de la imagen?
- O
- A
- F
- C
Solución:
Este reactivo tiene una sutileza que debe tomarse en cuenta para resolverlo correctamente. Recordemos que para la formación de imágenes en lentes convergentes, utilizamos dos rayos: el central y el paralelo.
En la figura, el rayo central es el número 3. Se dibuja lejos, porque la lente tiene un radio de curvatura bastante grande. Por otra parte, el rayo paralelo está denotado en la imagen con el número 1.
La imagen en una lente convergente se forma en la intersección entre el rayo 3 y el rayo 1, es decir, en el punto A.
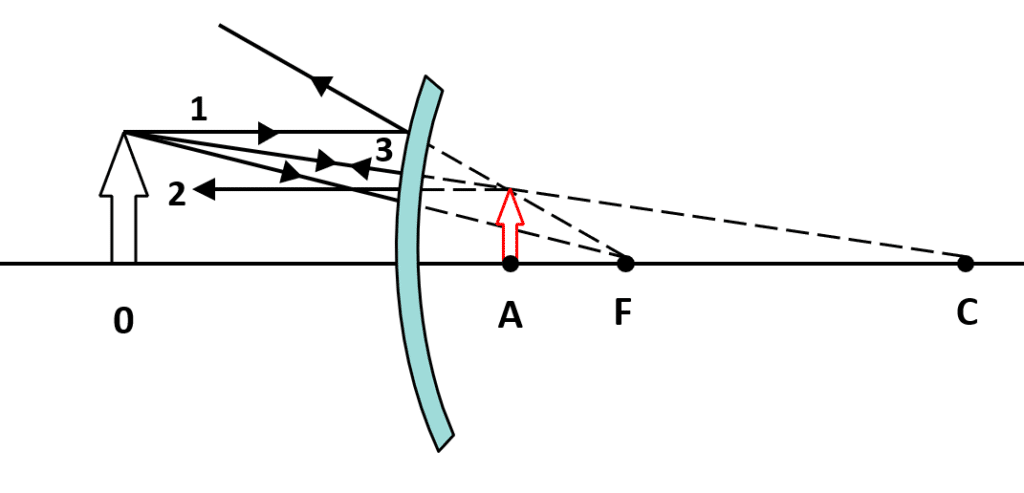
La respuesta correcta es el inciso b).


