Guía IPN Geometría y trigonometría del 41 al 50 resueltos

Prepararte para el examen de admisión del IPN es algo que debes tomarte muy enserio, ya que dependiendo de tu puntaje, serás admitido o no en la carrera que te interesa. Para ayudarte en tu preparación hemos preparado esta serie de 5 post en donde resolvemos los 50 reactivos del área de matemáticas, específicamente del campo de trigonometría y geometría.

Anterior

Te invitamos a seguir estudiando con nosotros, y ten presente que el examen del IPN comprende un total de 130 preguntas en dos partes diferentes. Por esto, es fundamental que te prepares muy bien y te mentalices a lograr el puntaje mínimo necesario para optar por un cupo en la carrera que deseas.

¿Qué viene en el examen del IPN?

Ten en mente que el examen de admisión del IPN está desglosado en dos partes distintas. La primera va dirigida a evaluar tus conocimientos generales en campos como la matemática y la comunicación. Luego, tendrás que presentar la segunda parte, la cual se dirige hacia ciencias más específicas como Física, Química y Biología.

Para que tengas una idea más clara de cómo es este examen, a continuación podrás ver la estructura del examen de admisión del Instituto Politécnico Nacional:

• 50 preguntas de matemáticas.
• 40 preguntas de comunicación.
• 10 preguntas de biología.
• 15 preguntas de química.
• 15 preguntas de física.

Sin más que añadir al respecto, ahora si te invitamos a ver los reactivos resueltos:

Reactivo 41: Determinar la expresión equivalente

Determinar la expresión equivalente para $\left(\operatorname{sen}^{4} y-\cos ^{4} y\right)$

1. $1-2 \cos y$
2. $1+2 \cos y$
3. $\cos 2 y$
4. $-\cos 2 y$

Solución:

Ya que ambos términos del binomio se están restando, en principio podemos factorizar por diferencia de cuadrados, quedando la expresión como:

$\left(\operatorname{sen}^{4} y-\cos ^{4} y\right)=\left(\operatorname{sen}^{2} y-\cos ^{2} y\right)\left(\operatorname{sen}^{2} y+\cos ^{2} y\right)$

Uno de los binomios conjugados es la identidad pitagórica, por lo que procedemos a sustituir 1 en su lugar:

$\left(\operatorname{sen}^{2} y-\cos ^{2} y\right)\left(\operatorname{sen}^{2} y+\cos ^{2} y\right)=\operatorname{sen}^{2} y-\cos ^{2} y$

Del coseno de la suma de ángulos sabemos que:

$\cos (x+y)=\cos x \cos y-\operatorname{sen} x \operatorname{sen} y$

Si ambos ángulos son el mismo:

$\cos (y+y)=\cos (2 y)=\cos ^{2} y-\operatorname{sen}^{2} y$

Extraemos finalmente factor común el signo menos y sustituimos en la expresión:

$-\cos (2 y)=\operatorname{sen}^{2} y-\cos ^{2} y$

$\left(\operatorname{sen}^{2} y-\cos ^{2} y\right)\left(\operatorname{sen}^{2} y+\cos ^{2} y\right)=\operatorname{sen}^{2} y-\cos ^{2} y=-\cos (2 y)$

Concluimos de esta forma que:

$\left(\operatorname{sen}^{4} y-\cos ^{4} y\right)=-\cos (2 y)$

De todas las opciones, la correcta seria la d).

Reactivo 42: Simplificar la siguiente función

Simplificar la siguiente función trigonométrica: $\tan ^{4} \beta-2 \tan ^{2} \beta \sec ^{2} \beta+\sec ^{4} \beta$

1. -1
2. 1
3. $\tan ^{2} \beta$
4. $\tan ^{4} \beta$

Solución:

A simple vista, en este problema podemos aplicar la factorización por binomio cuadrado perfecto, específicamente la de la resta ya que se comprueba que:

$(a-b)^{2}=a^{2}-2 a b+b^{2}$

$2 \sqrt{\tan ^{4} \beta \sec ^{4} \beta}=2 \tan ^{2} \beta \sec ^{2} \beta$

Resolviendo la raíz para ambas potencias:

$2 \tan ^{2} \beta \sec ^{2} \beta=2 \tan ^{2} \beta \sec ^{2} \beta$

Donde:

$a=\tan ^{2} \beta \text { y } b=\sec ^{2} \beta$

$\tan ^{4} \beta-2 \tan ^{2} \beta \sec ^{2} \beta+\sec ^{4} \beta=\left(\tan ^{2} \beta-\sec ^{2} \beta\right)^{2}$

Esta forma puede seguir siendo simplificada, si sustituimos a la identidad pitagórica en términos de la tangente y la secante:

$\tan ^{2} \beta+1=\sec ^{2} \beta \rightarrow \tan ^{2} \beta-\sec ^{2} \beta=-1$

$\left(\tan ^{2} \beta-\sec ^{2} \beta\right)^{2}=(-1)^{2}=1$

Se concluye entonces que:

$\tan ^{4} \beta-2 \tan ^{2} \beta \sec ^{2} \beta+\sec ^{4} \beta=1$

Según las opciones que ofrece el problema, la respuesta correcta seria la b).

Reactivo 43: Identificar el seno

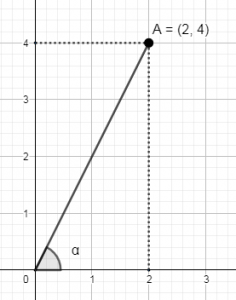
Identificar el $\sin \alpha$ dada la siguiente figura:

1. $\frac{4}{\sqrt{20}}$
2. $\frac{\sqrt{20}}{4}$
3. $\frac{2}{4}$
4. $\frac{4}{2}$

Solución:

Por definición, el seno de un determinado ángulo es: cateto opuesto sobre hipotenusa.

$\sin \alpha=\frac{C O}{H}$

Nuestro ángulo es alfa, que tiene como cateto opuesto a 4 y como hipotenusa la distancia al punto $A(2,4)$ medida desde el origen de coordenadas. Dicha hipotenusa se puede determinar con ayuda del Teorema de Pitágoras:

$h=\sqrt{2^{2}+4^{2}}=\sqrt{4+16}=\sqrt{20}$

Tengamos en cuenta que, el valor final del seno tiene que ser positivo porque nos encontramos en el primer cuadrante. El seno es positivo en el primer y segundo cuadrante y negativo en el tercero y el cuarto.

$\sin \alpha=\frac{4}{\sqrt{20}}$

Concluimos entonces que la respuesta correcta es la a).

Reactivo 44: Determinar la igualdad

Determinar la igualdad de la expresión: $\frac{1}{1+\cos \theta}$

1. $\frac{1}{2} \operatorname{sen}^{2} \frac{\theta}{2}$
2. $\frac{1}{2} \cos ^{2} \frac{\theta}{2}$
3. $\frac{1}{2} \sec ^{2} \frac{\theta}{2}$
4. $\frac{1}{2} \csc ^{2} \frac{\theta}{2}$

Solución:

A primera vista, la expresión se encuentra solo en términos de coseno. Además, parece que no tiene mayor simplificación pero con algunos trucos, podremos llevarla a una sola identidad más compacta.

Comencemos multiplicando y dividiendo por el conjugado de $1+\cos \theta$:

$\frac{1}{1+\cos \theta} \cdot \frac{1-\cos \theta}{1-\cos \theta}=\frac{1-\cos \theta}{1-\cos ^{2} \theta}$

El denominador podemos sustituirlo por $\operatorname{sen}^{2} \theta$ según la identidad pitagórica:

$\operatorname{sen}^{2} \theta+\cos ^{2} \theta=1 \rightarrow \operatorname{sen}^{2} \theta=1-\cos ^{2} \theta$

$\frac{1-\cos \theta}{1-\cos ^{2} \theta}=\frac{1-\cos \theta}{\operatorname{sen}^{2} \theta}$

Ahora es cuando nos toca ser audaces trabajando con las identidades y las sumas de ángulos. Como el denominador ha quedado compacto en una misma expresión, queda trabajar con el numerador.

Comencemos por $\cos \theta$. Por simple aritmética, sabemos que:

$\cos \theta=\cos \left(\frac{\theta}{2}+\frac{\theta}{2}\right)$

Recordando la propiedad de suma de ángulos para el coseno:

$\cos (x+y)=\cos x \cos y-\operatorname{sen} x \operatorname{sen} y$

Podemos expresar a $\cos \left(\frac{\theta}{2}+\frac{\theta}{2}\right)$ como:

$\cos \left(\frac{\theta}{2}+\frac{\theta}{2}\right)=\cos \frac{\theta}{2} \cos \frac{\theta}{2}-\operatorname{sen} \frac{\theta}{2} \operatorname{sen} \frac{\theta}{2}=\cos ^{2} \frac{\theta}{2}-\operatorname{sen}^{2} \frac{\theta}{2}$

Llegados a este punto, la expresión se parece mucho a $1-\cos \theta$, solo que el coseno esta positivo y falta el uno. Al ser una igualdad la identidad que tenemos, podemos multiplicar a ambos lados por -1 y luego sumar 1, también a ambos lados.

Multiplicando por -1:

$\cos \theta=\cos ^{2} \frac{\theta}{2}-\operatorname{sen}^{2} \frac{\theta}{2} \rightarrow-\cos \theta=-\cos ^{2} \frac{\theta}{2}+\operatorname{sen}^{2} \frac{\theta}{2}$

Sumamos ahora 1 a ambos lados:

$-\cos \theta=-\cos ^{2} \frac{\theta}{2}+\operatorname{sen}^{2} \frac{\theta}{2} \rightarrow 1-\cos \theta=1-\cos ^{2} \frac{\theta}{2}+\operatorname{sen}^{2} \frac{\theta}{2}$

Por último, aplicamos la identidad pitagórica a $1-\cos ^{2} \frac{\theta}{2}$ que es igual a $\operatorname{sen}^{2} \frac{\theta}{2}$:

$1-\cos \theta=\operatorname{sen}^{2} \frac{\theta}{2}+\operatorname{sen}^{2} \frac{\theta}{2}=2 \operatorname{sen}^{2} \frac{\theta}{2}$

Sustituimos en el numerador de la expresión que estamos intentando transformar:

$\frac{1-\cos \theta}{\operatorname{sen}^{2} \theta}=\frac{2 \operatorname{sen}^{2} \frac{\theta}{2}}{\operatorname{sen}^{2} \theta}$

Ahora, aunque ambas funciones trigonométricas son senos, no es posible aplicar ninguna simplificación por exponentes, ya que los argumentos son distintos. Toca transformar al denominador. Emplearemos el mismo truco de la suma de ángulos, pero esta vez para el seno:

$\operatorname{sen} \theta=\operatorname{sen}\left(\frac{\theta}{2}+\frac{\theta}{2}\right)$

Recordando la propiedad de suma de ángulos para el seno:

$\operatorname{sen}(x+y)=\operatorname{sen} x \cos y+\cos x \operatorname{sen} y$

$\operatorname{sen}\left(\frac{\theta}{2}+\frac{\theta}{2}\right)=\operatorname{sen} \frac{\theta}{2} \cos \frac{\theta}{2}+\cos \frac{\theta}{2} \operatorname{sen} \frac{\theta}{2}$

Sumando nos queda que:

$\operatorname{sen} \theta=2 \operatorname{sen} \frac{\theta}{2} \cos \frac{\theta}{2}$

Si elevamos ambos miembros al cuadrado:

$\operatorname{sen}^{2} \theta=4 \operatorname{sen}^{2} \frac{\theta}{2} \cos ^{2} \frac{\theta}{2}$

Podemos finalmente sustituir el denominador por funciones que tienen el mismo argumento que el numerador:

$\frac{2 \operatorname{sen}^{2} \frac{\theta}{2}}{\operatorname{sen}^{2} \theta}=\frac{2 \operatorname{sen}^{2} \frac{\theta}{2}}{4 \operatorname{sen}^{2} \frac{\theta}{2} \cos ^{2} \frac{\theta}{2}}=\frac{1}{2} \frac{1}{\cos ^{2} \frac{\theta}{2}}$

Aplicamos una última identidad, sabiendo que:

$\cos x=\frac{1}{\sec x} \rightarrow \sec x=\frac{1}{\cos x}$

$\frac{1}{2} \frac{1}{\cos ^{2} \frac{\theta}{2}}=\frac{1}{2} \sec ^{2} \frac{\theta}{2}$

Concluimos finalmente, luego de todas estas transformaciones:

$\frac{1}{1+\cos \theta}=\frac{1}{2} \sec ^{2} \frac{\theta}{2}$

Según las opciones que ofrece el problema, la respuesta correcta seria la c). Para resolver este ejercicio, se pudo haber empleado otras identidades que reducían muchas transformaciones intermedias, pero hemos decidido dejarlas para que tengas una idea de cómo se pueden combinar identidades y propiedades.

La recomendación general será que continúes practicando, analiza cada paso que des y no tengas miedo de probar cualquier cosa que se te ocurra, equivocarte e intentarlo de nuevo. La práctica hace al maestro.

Reactivo 45: Identidad trigonométrica pitagórica

La identidad ________ $+\cos ^{2} x=1$ es una identidad trigonométrica pitagórica.

1. $\cos ^{2} x$
2. $\tan ^{2} x$
3. $\cot ^{2} x$
4. $\operatorname{sen}^{2} x$

Solución:

A partir de la circunferencia trigonométrica, se deduce la identidad pitagórica y sus equivalentes:

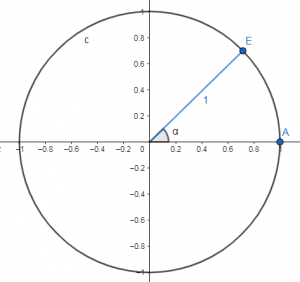
El coseno y el seno del ángulo alfa serian:

$\cos \alpha=\frac{C A}{H}=\frac{C A}{1}=C A$

$\sin \alpha=\frac{C O}{H}=\frac{C O}{1}=C O$

Ahora, según el teorema de Pitágoras para triángulos rectángulos:

$h^{2}=C A^{2}+C O^{2}$

Sustituyendo las identidades anteriores:

$1^{2}=\cos \alpha^{2}+\sin \alpha^{2}$

$1=\cos \alpha^{2}+\sin \alpha^{2}$

Obtenemos a la identidad pitagórica en términos de senos y coseno. Según se divide la expresión por $\cos \alpha^{2}$ o $\sin \alpha^{2}$ se obtienen el resto de identidades pitagóricas equivalentes. Concluimos entonces que la respuesta correcta es la opción d).

Es claro que no necesitas demostrar la identidad para responder la pregunta, la recomendación general para cualquier examen es que sepas la mayor cantidad de identidades trigonométricas que puedas. Se ha hecho en esta ocasión para evidenciar el origen de la formula.

Reactivo 46: Calcular el seno

Calcular el $\sin 15^{\circ}$, aplicando el valor exacto del $\cos 30^{\circ}$

1. $\frac{\sqrt{2+\sqrt{3}}}{2}$
2. $\frac{\sqrt{2+\sqrt{3}}}{4}$
3. $\frac{\sqrt{2-\sqrt{3}}}{2}$
4. $\frac{\sqrt{2-\sqrt{3}}}{4}$

Solución:

En este problema aplicaremos un pequeño truco con las identidades de suma de ángulos. Partiremos desde el $\cos 30^{\circ}$ escrito como $\cos \left(15^{\circ}+15^{\circ}\right)$, para aplicar la identidad de la suma de ángulos para el coseno.

$\cos (x+y)=\cos x \cos y-\sin x \sin y$

$\cos \left(15^{\circ}+15^{\circ}\right)=\cos 15^{\circ} \cos 15^{\circ}-\sin 15^{\circ} \sin 15^{\circ}$

Expresamos los productos como potencias:

$\cos \left(15^{\circ}+15^{\circ}\right)=\cos 30^{\circ}=\cos ^{2} 15^{\circ}-\sin ^{2} 15^{\circ}$

Aplicamos la identidad pitagórica para deshacernos del $\cos ^{2} 15^{\circ}$:

$\cos ^{2} 15^{\circ}+\sin ^{2} 15^{\circ}=1$

Despejando nos queda que:

$\cos ^{2} 15^{\circ}=1-\sin ^{2} 15^{\circ}$

Sustituimos ahora en la expresión original:

$\cos 30^{\circ}=1-\sin ^{2} 15^{\circ}-\sin ^{2} 15^{\circ}=1-2 \sin ^{2} 15^{\circ}$

Finalmente, despejamos a $\sin ^{2} 15^{\circ}$:

$\cos 30^{\circ}=1-2 \sin ^{2} 15^{\circ}$

$2 \sin ^{2} 15^{\circ}=1-\cos 30^{\circ}$

$\sin ^{2} 15^{\circ}=\frac{1-\cos 30^{\circ}}{2}$

$\sin 15^{\circ}=\pm \sqrt{\frac{1-\cos 30^{\circ}}{2}}$

Tomaremos solo el valor positivo, porque 15° es un ángulo que se encuentra en el primer cuadrante y el seno es positivo en dicha región.

$\sin 15^{\circ}=\sqrt{\frac{1-\cos 30^{\circ}}{2}}$

Sustituimos $\cos 30^{\circ}=\frac{\sqrt{3}}{2}$

$\sin 15^{\circ}=\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{2}}=\sqrt{\frac{2-\sqrt{3}}{4}}$

$\sin 15^{\circ}=\frac{\sqrt{2-\sqrt{3}}}{2}$

Concluimos entonces que la respuesta correcta es la opción c).

Reactivo 47: Obtén la razón trigonométrica

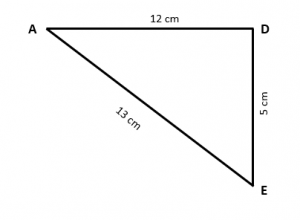
Para el siguiente triangulo rectángulo, la razón trigonométrica $\sin A$ es:

1. 5/13
2. 5/12
3. 12/13
4. 13/15

Solución:

El problema se reduce en conocer la definición de la relación trigonométrica seno del ángulo.

$\sin A=\frac{C O}{H}$

Cuando el enunciado dice $\sin A$, hace referencia al seno del ángulo formado en ese vértice del triángulo, es decir entre el cateto que mide 12 cm y la hipotenusa de 13 cm.

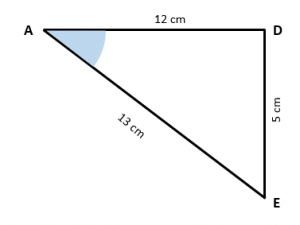
Para el ángulo $A$, el cateto opuesto seria el lado 5 cm y la hipotenusa 13 cm. Sustituimos en la definición del seno:

$\sin A=\frac{5 \mathrm{~cm}}{13 \mathrm{~cm}}=\frac{5}{13}$

Concluimos entonces que la respuesta correcta es la opción a).

Reactivo 48: Identificar el valor de la función

Identificar el valor de la función trigonométrica $\tan \alpha$ utilizando el triángulo siguiente:

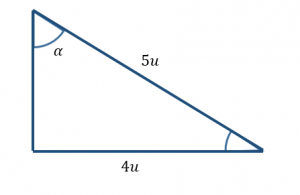
1. 4/5
2. 3/5
3. 4/3
4. 5/3

Solución:

Para calcular la tangente de alfa, necesitamos el cateto opuesto y el cateto adyacente a dicho ángulo. Gracias a la ilustración, sabemos que el cateto opuesto a alfa vale $4 u$, pero no hay información respecto al cateto adyacente.

$\tan \alpha=\frac{4 u}{C A}$

Como dato extra, el problema nos da la magnitud de la hipotenusa. Si empleamos el Teorema de Pitágoras en el triángulo rectángulo, podríamos calcular al cateto faltante.

$h^{2}=C O^{2}+C A^{2}$

$C A=\sqrt{h^{2}-C O^{2}}$

$C A=\sqrt{5^{2}-4^{2}}=\sqrt{9}=3$

$C A=3 u$

Sustituyendo en la tangente nos queda:

$\tan \alpha=\frac{4 u}{3 u}=\frac{4}{3}$

Concluimos entonces que la respuesta es la opción c).

Reactivo 49: Expresión equivalente

¿Cuál de las siguientes expresiones es equivalente a $\csc ^{2} \theta \operatorname{sen} \theta$?

1. $\cos ^{2} \theta$
2. $\tan \theta$
3. $\sec \theta$
4. $\csc \theta$

Solución:

La expresión no se encuentra escrita en uno de los pares sugeridos para simplificar la demostración. Procedemos entonces a sustituir:

$\csc ^{2} \theta=\frac{1}{\operatorname{sen}^{2} \theta} \rightarrow \frac{1}{\operatorname{sen}^{2} \theta} \operatorname{sen} \theta=\frac{1}{\operatorname{sen} \theta}$

Ahora, transformamos al inverso del seno del ángulo como la secante del ángulo, para que nuestra respuesta tenga concordancia con las opciones ofrecidas por el problema:

$\csc ^{2} \theta \operatorname{sen} \theta=\frac{1}{\operatorname{sen} \theta}=\csc \theta$

Concluimos entonces que la respuesta es la d).

Reactivo 50: Determinar la igualdad de la expresión

Determinar la igualdad de la expresión: $\left(\cos \frac{t}{6}-\operatorname{sen} \frac{t}{6}\right)^{2}$

1. $\cos ^{2} \frac{t}{3}$
2. $1-\operatorname{sen} \frac{t}{3}$
3. $\cos ^{2} \frac{t}{6}+\operatorname{sen}^{2} \frac{t}{6}$
4. $\cos ^{2} \frac{t}{6}-\operatorname{sen}^{2} \frac{t}{6}$

Solución:

Antes de pasar a desarrollar el producto notable, nos damos cuenta que la expresión está escrita en uno de los pares sugeridos antes: seno y coseno, por lo que no es necesario hacer alguna otra transformación. Desarrollamos entonces la potencia:

$\left(\cos \frac{t}{6}-\operatorname{sen} \frac{t}{6}\right)^{2}=\cos ^{2} \frac{t}{6}-2 \cos \frac{t}{6} \operatorname{sen} \frac{t}{6}+\operatorname{sen}^{2} \frac{t}{6}$

Si recordamos, la identidad Pitagórica indica que:

$\cos ^{2} x+\operatorname{sen}^{2} x=1$

Al agrupar $\cos ^{2} \frac{t}{6} \text{ y } \operatorname{sen}^{2} \frac{t}{6}$, podemos aplicar esta identidad básica:

$\left(\cos \frac{t}{6}-\operatorname{sen} \frac{t}{6}\right)^{2}=\left(\cos ^{2} \frac{t}{6}+\operatorname{sen}^{2} \frac{t}{6}\right)-2 \cos \frac{t}{6} \operatorname{sen} \frac{t}{6}=1-2 \cos \frac{t}{6} \operatorname{sen} \frac{t}{6}$

Llegados a este punto, probemos deducir del seno de la suma y resta de dos ángulos:

$\operatorname{sen}(x+y)=\operatorname{sen} x \cos y+\operatorname{sen} y \cos x$

$\operatorname{sen}(x-y)=\operatorname{sen} x \cos y-\operatorname{sen} y \cos x$

Se suman ambas identidades para obtener:

$\operatorname{sen}(x+y)+\operatorname{sen}(x-y)=\operatorname{sen} x \cos y+\operatorname{sen} y \cos x+\operatorname{sen} x \cos y-\operatorname{sen} y \cos x$

$\operatorname{sen}(x+y)+\operatorname{sen}(x-y)=2 \operatorname{sen} x \cos y$

Si $x \text { у } y$ son ambos iguales a $\frac{t}{6}$:

$\operatorname{sen}\left(\frac{t}{6}+\frac{t}{6}\right)+\operatorname{sen}\left(\frac{t}{6}-\frac{t}{6}\right)=2 \operatorname{sen} \frac{t}{6} \cos \frac{t}{6}$

Sustituimos en el punto que quedamos:

$\left(\cos \frac{t}{6}-\operatorname{sen} \frac{t}{6}\right)^{2}=1-\operatorname{sen}\left(\frac{t}{6}+\frac{t}{6}\right)-\operatorname{sen}\left(\frac{t}{6}-\frac{t}{6}\right)=1-\operatorname{sen}\left(\frac{t}{3}\right)$

Concluimos finalmente con la simplificación:

$\left(\cos \frac{t}{6}-\operatorname{sen} \frac{t}{6}\right)^{2}=1-\operatorname{sen}\left(\frac{t}{3}\right)$

La respuesta correcta, según las opciones dadas por el problema, sería la b).