¡Hola aspirante! En este tutorial resolveremos la primera parte de la Guía Interactiva de EXANI II, para el módulo de Aritmética, desde el reactivo 1 hasta el 12.

Te aconsejo resolver los problemas por tu cuenta antes de mirar la solución. Es importante que desarrolles tu capacidad de análisis y solución de problemas antes del examen.Añadid
Estructura del EXANI II
El examen de ingreso EXANI II diseñado por CENEVAL, se divide en dos partes:
- Habilidades y conocimientos
- Los módulos específicos.
Algunas universidades aplican una prueba diagnóstico de inglés extra, la cual no cuenta para aprobar el examen.
Examen de habilidades y conocimientos
La primera parte del examen se aplica de igual forma para todas las carreras y consta de 90 reactivos: 60 de Español y 30 de Matemáticas. La siguiente tabla resume la distribución de los reactivos en la prueba:
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Por otro lado, en la segunda parte los estudiantes deben responder 2 módulos, los cuales varían de acuerdo a la carrera. Es necesario que revises la convocatoria de tu universidad para conocer cuáles de los 15 módulos van para tu examen.
Módulos de los conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Aritmética EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de aritmética, con el temario desglosado que va para el examen.
| Subárea | Reactivos |
|---|---|
| Principios de números reales | 14 |
| Problemas con números reales | 10 |
| Total | 24 |
Subárea: Principios de números reales
- Operaciones básicas con números enteros, fracciones y decimales
- Ley de los signos
- Potenciación
- Signos de agrupación
- Expresiones algebraicas con radicales
- Notación científica
- Factores primos
- Reglas de divisibilidad
- Mínimo común múltiplo
- Máximo común divisor
Subárea: Problemas con números racionales
- Razón y proporción
- Porcentaje
- Progresión geométrica
- Progresión aritmética
- Reparto proporcional
- Interés simple
- Regla de tres
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Un apicultor que produce miel y propóleo desea envasar la totalidad de su producción en recipientes iguales de la máxima capacidad posible. En sus últimas cosechas obtuvo 256 y 96 L, respectivamente.
¿Cuál tiene que ser la capacidad de los recipientes, expresada en litros?
- 16
- 32
- 48
Solución:
El enunciado nos pide determinar la capacidad que deben tener los envases seleccionados, para envasar con ellos la mayor cantidad de miel y propóleo respectivamente. El problema se resuelve calculando el máximo común divisor de 256 y 96.
Primero, se descomponen en factores primos a los números.

Se expresan las cantidades como el producto de potencias de factores primos.
256={2}^{8}, 96={2}^{5}\cdot 3
Ahora, se toman los factores comunes con el menor exponente. El único factor común es el 2 con exponente 5. Por lo tanto, los envases deben tener una capacidad de {2}^{5}=32 \mathrm{l}\mathrm{i}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s} . La respuesta correcta es el inciso b).
La opción a) es incorrecta porque, aunque es divisor de ambas capacidades, no es máximo. Probablemente hayas recurrido al tanteo de los incisos, este método ofrece rapidez, pero debes comprobar el resultado obtenido para tener la certeza en tu respuesta.
Por otra parte, el inciso c) indica un número que es divisor solo de 96, debido a que 256 no tiene división exacta por 48.
Reactivo 2
Con el 18% de descuento aplicado, un traje cuesta $2,050. ¿Cuál es su precio original?
- 1681
- 2419
- 2500
Solución:
Debemos recurrir a la fórmula para aplicar descuento a una transacción:
{P}^{\text{'}}=P\left(1-D\right)
Donde P\text{'} es el nuevo precio, P es el precio original y D es el descuento expresado en decimales. En este caso tenemos que {P}^{\text{'}}=2050 y D=0.18 , despejamos P de la ecuación y sustituimos los valores dados.
P=\frac{P\text{'}}{1-D}=\frac{2050}{1-0.18}=\frac{2050}{0.82}=2500\$
El precio original del traje fue de $2500.
La respuesta correcta es el inciso c). El error en el inciso a) es que se aplica el descuento al monto de 2050$, cuando en realidad este es el precio ya con descuento y se solicita el original.
Por otra parte, el error en el inciso b) consiste en aplicarle el 18% de incremento al precio con descuento, lo cual no es equivalente a encontrar el precio original.
Reactivo 3
Un hombre depositó $30,000 en un banco a un plazo de 5 años. Al término del periodo, retiró $48,000, los cuales corresponden al capital inicial más el interés.
Identifique la tasa de interés simple anual que pagó el banco.
- 12%
- 32%
- 60%
Solución:
Aunque el problema no lo indica, debemos utilizar la fórmula de interés simple para resolver el problema.
R=P\left(1+in\right)
Donde R es el monto al final del período, n es el total de períodos, i es la tasa de interés y P es la inversión inicial. Despejamos el interés de la ecuación.
R=P\left(1+in\right)\to \frac{R}{P}=1+in
in=\frac{R}{P}-1
i=\frac{1}{n}\left(\frac{R}{P}-1\right)
Sustituimos los valores dados.
i=\frac{1}{5}\left(\frac{48000}{30000}-1\right)=\frac{1}{5}\left(0.6\right)=0.12
Expresada en porcentaje, la tasa de interés fue del 12%.
La respuesta correcta es el inciso a). En el inciso b), se divide el total del monto retirado entre los 5 años y lo que resultó, entre el capital invertido. El error de cálculo se debe a que se consideró al capital invertido como parte de la ganancia.
Por otra parte, el inciso c) calcula el porcentaje total de ganancia respecto al monto inicial, pero olvida dividir el resultado obtenido por los 5 años.
Reactivo 4
Diariamente, una fábrica produce 5.000 pantalones con 10 máquinas en un tiempo de 5 horas. Si se sabe que 2 máquinas estarán en mantenimiento y no podrán operar, ¿Cuántas horas se incrementará el tiempo de producción diario?
- 1.25
- 4.00
- 6.25
Solución:
Para resolver el problema, es necesario aplicar una regla de tres. Iniciamos identificando las variables del problema. Estas son: el número de pantalones, el número de máquinas y el tiempo de la jornada de trabajo.
En ambos casos, el número de pantalones es igual ya que se pretende mantener la misma producción. Por lo tanto, la regla de tres se aplica entre el número de máquinas y el tiempo. La relación debe ser inversa, porque a menor cantidad de máquinas más tiempo se debe trabajar.

Regla de tres, inversa.
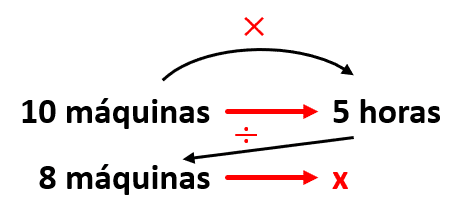
x=\frac{\left(10\right)\left(5\right)}{8}=6.25 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
Con 8 máquinas se debe trabajar, al menos, 6.25 horas. Es decir, a las 5 horas actuales se deben adicionar 1.25 horas extra. La respuesta correcta es el inciso a). En el inciso b) se utiliza una relación directa y no como inversa.
En la opción c), se ha considerado una relación inversa al tiempo de producción, pero no se calculó la variación respecto a las horas de trabajo actuales. Este resultado corresponde con la duración de la jornada laboral completa y no al incremento respecto a las 5 horas.
Reactivo 5
Una empresa tiene 5 departamentos, cada uno de ellos con diferente número de extensiones telefónicas. El Almacén cuenta con 4 extensiones; Mantenimiento, con 3; Producción, con 4; Control de Calidad, con 7, y Ventas, con 3. La empresa dicta que el pago del servicio telefónico se realiza en forma proporcional al número de extensiones de cada departamento. Para este mes, el recibo asciende a $28,412.00.
¿Cuánto debe pagar el Departamento de Ventas por el servicio?
- $4,058.86
- $5,682.40
- $9,470.67
Solución:
Para calcular el pago por departamento, se divide el total de extensiones asociadas al departamento por el total de extensiones en la empresa (21 en este caso) y el resultado se multiplica por el monto de la factura.
Llevando esto al departamento de ventas, se obtiene:
\mathrm{P}\mathrm{V}=\frac{3}{21}\cdot 28412=\frac{1}{7}\cdot 28412=4058.86\$
El departamento de ventas debe pagar 4058.86\$ por las 3 extensiones instaladas. La respuesta correcta es el inciso a). El inciso b) es incorrecto, porque divide la cuenta por igual entre los 5 departamentos, pero no considera la cantidad de extensiones en ellos.
Por otra parte, el inciso c) divide el monto total por el número de extensiones en la empresa, pero no multiplica por las extensiones en el departamento de ventas. En este caso se calcula el costo unitario por extensión.
Reactivo 6
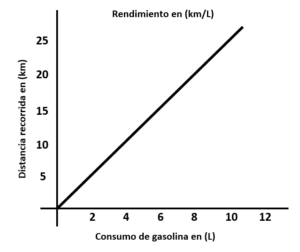
Identifique la gráfica que representa el rendimiento de combustible, equivalente a 10 km/L, de una camioneta.
Solución:
Debido a que todas las gráficas son líneas rectas, la razón de km/L se obtiene calculando la pendiente de las rectas. La respuesta será correcta si la pendiente es igual a 10 km/L. Recordemos que la pendiente de una recta se calcula como:
m=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}
Pendiente de la gráfica a.
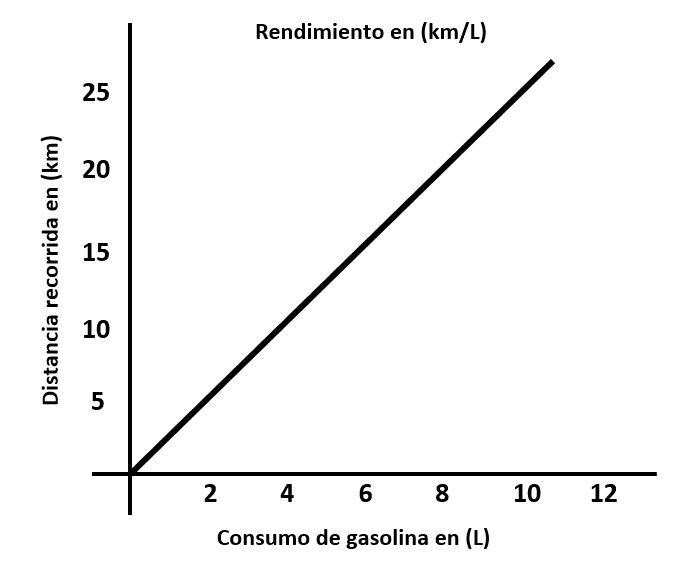
Se identifica que para 10 litros se recorren 25 kilómetros.
m=\frac{25}{10}=2.5\frac{\mathrm{k}\mathrm{m}}{\mathrm{L}}
No es la respuesta correcta.
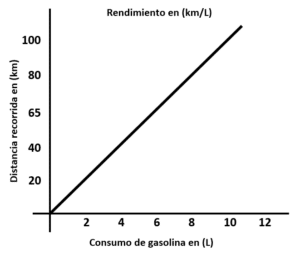
Pendiente de la gráfica b.
Se identifica que con 10 litros se recorren 100 kilómetros.
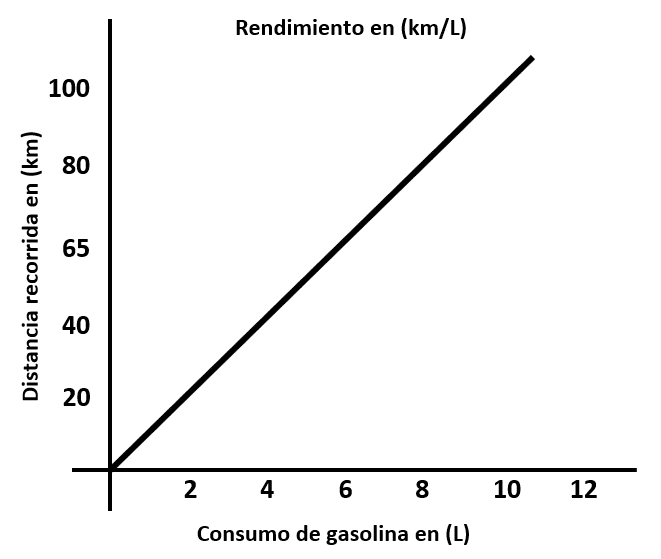
m=\frac{100}{10}=10\frac{\mathrm{k}\mathrm{m}}{\mathrm{L}}
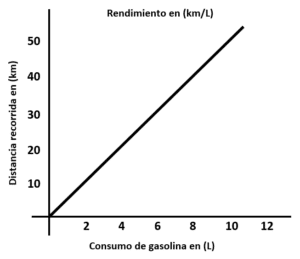
La gráfica que representa el rendimiento de combustible solicitado es la del inciso b). Al igual que el inciso a), el c) es incorrecto porque el rendimiento es de 5 km/L, el cual se puede determinar al dividir 50 km con 10 litros.
Reactivo 7
Identifique la producción realizada en 6 horas.
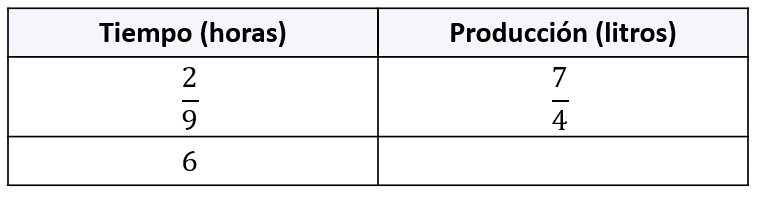
- \frac{189}{4}
- \frac{7}{108}
- \frac{16}{21}
Solución:
Para completar la casilla restante, se aplica una regla de 3 directa, debido a que mientras más tiempo se mantenga la empresa funcionando, mayor será la producción. Se multiplica el 6 por \frac{7}{4} y el resultado se divide por \frac{2}{9} .
x=\frac{\left(6\right)\left(\frac{7}{4}\right)}{\frac{2}{9}}=\frac{\frac{21}{2}}{\frac{2}{9}}=\frac{189}{4}
Comparando con los incisos, se concluye que la respuesta correcta es el a). Tanto en el inciso b) como en el c), no se aplican reglas de tres. Por esta razón los resultados son incorrectos. En el b) se calcula \frac{2}{9}\times \frac{\frac{7}{4}}{6} y en el c) 6\times \frac{\frac{2}{9}}{\frac{7}{4}} .
Reactivo 8
Identifique la solución de la siguiente expresión.
72 ÷ 8 + 3 - 4 \times 5 + 4 \times {2}^{2} ÷ 2 – 6
- -6
- -1
- 82
Solución:
Para encontrar la respuesta correcta, debemos seguir las reglas de las operaciones matemáticas elementales:
- Paréntesis, corchetes y llaves
- Exponentes y radicales
- Multiplicaciones y divisiones
- Sumas y restas
Teniendo en cuenta que se resuelven de izquierda a derecha. En este caso, se inicia calculando la potencia {2}^{2} .
=72 ÷ 8 + 3 - 4 \times 5 + 4 \times 4 ÷ 2 – 6
Ahora, se resuelven las mutilaciones y divisiones de izquierda a derecha.
=9 + 3 - 20 + 16 ÷ 2 – 6
=9 + 3 - 20 + 8 – 6
Finalmente, se calculan sumas y restas.
=12 - 20 + 8 – 6
=-8+8-6
=-6
La respuesta correcta es el inciso a). El error en el inciso b) fue realizar las operaciones comenzando por las sumas y restas, mientras que en el inciso c) no se respetó la jerarquía de operaciones, pues se realizaron de forma secuencial de izquierda a derecha.
Reactivo 9
Identifique la representación en lenguaje común correspondiente a la siguiente expresión matemática.
{7}^{\frac{4}{3}}
- Raíz cuarta de siete elevado al cubo
- Tercera parte de siete elevado a la cuarta potencia
- Raíz cúbica de siete elevado a la cuarta potencia
Solución:
Primero se convierte la potencia con exponente fraccionario a radical. El denominador de la fracción pasa a ser el índice de la raíz.
{7}^{\frac{4}{3}}=\sqrt[3]{{7}^{4}}
Ahora, debemos escribir la operación en lenguaje común:
Raíz cúbica de siete elevada a la cuarta potencia.
La respuesta correcta es el inciso c). En el inciso a) se aplica incorrectamente la propiedad del exponente fraccionario, mientras que en el inciso b) se toma el 3 y se divide al 7 por él, para luego elevar todo por 4, esta operación no tiene ningún fundamento.
Reactivo 10
Identifique los factores primos del número 350.
- 2, 3, 7
- 2, 5, 7
- 5, 7, 13
Solución:
Se descompone el 350 en sus factores primos.
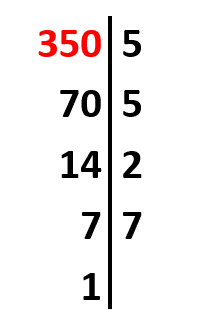
Los factores primos del 350 son: 2, 5 y 7.
La respuesta correcta es el inciso b). Tanto en el inciso a) como en el c) se indican números primos que no son factores del 350.
Reactivo 11
La tripulación de un barco está conformada por 70 personas. Se cuenta con alimento para 18 días con 3 comidas diarias. Si se disminuyen las raciones a 2 comidas diarias y se aumenta la tripulación con 15 personas, ¿Cuántos días durarán los alimentos?
- 21.85
- 22.23
- 32.78
Solución:
Primero se calcula el total de comidas durante los 18 días de viaje iniciales. Hay que tener en cuenta que son 3 comidas al día por persona 3\frac{\mathrm{c}}{\mathrm{d}\mathrm{í}\mathrm{a}\cdot \mathrm{p}} .
{\mathrm{C}\mathrm{T}}_{1}=70 \mathrm{p}\cdot 3\frac{\mathrm{c}}{\mathrm{d}\mathrm{í}\mathrm{a}\cdot \mathrm{p}}\cdot 18 \mathrm{d}\mathrm{í}\mathrm{a}=3780\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}
El primer viaje implicaba 3780 porciones de comida para viajar durante 18 días. Ahora, se reducen las porciones de comida a 2 comidas al día por persona 2\frac{\mathrm{c}}{\mathrm{d}\mathrm{í}\mathrm{a}\cdot \mathrm{p}} y la tripulación sube a 85 personas. Para obtener los días, se dividen las 3780 porciones entre el producto de 2\frac{\mathrm{c}}{\mathrm{d}\mathrm{í}\mathrm{a}\cdot \mathrm{p}} con 85 \mathrm{p} .
\mathrm{D}\mathrm{í}{\mathrm{a}\mathrm{s}}_{2}=\frac{3780 \mathrm{c}}{2\frac{\mathrm{c}}{\mathrm{d}\mathrm{í}\mathrm{a}\cdot \mathrm{p}}\cdot 85 \mathrm{p}}
Simplificamos unidades y resolvemos las operaciones.
\mathrm{D}\mathrm{í}{\mathrm{a}\mathrm{s}}_{2}=\frac{3780 }{2\frac{1}{\mathrm{d}\mathrm{í}\mathrm{a}}\cdot 85}=\frac{3780}{170} \mathrm{d}\mathrm{í}\mathrm{a}=22.24 \mathrm{d}\mathrm{í}\mathrm{a}
Cuando las opociones se reducen a 2 diarias por persona y se integran 15 tripulantes, la comida alcanza para 22.24 días. La respuesta correcta es el inciso b).
El uso de unidades en estos ejercicios es bastante útil, ya que permite saber a qué corresponde el resultado que hemos obtenido. El inciso a) sólo relaciona de forma directa las personas con los días.
\frac{18 \mathrm{d}\cdot 85\mathrm{ }\mathrm{p}}{70 \mathrm{p}}=21.85 \mathrm{d}\mathrm{í}\mathrm{a}
Este resultado significa que mientras más personas se añaden a la tripulación, el viaje durará más días, pero esto no tiene sentido cuando no se toma en cuenta la comida. Por otra parte, la opción c) invierte la razón de personas:
\frac{85\mathrm{p}\cdot 3\frac{\mathrm{c}}{\mathrm{d}\cdot \mathrm{p}}\cdot 18\mathrm{ }\mathrm{d}}{70\mathrm{p}\cdot 2\frac{\mathrm{c}}{\mathrm{d}\cdot \mathrm{p}}}=\frac{4590 \mathrm{c}}{140\frac{\mathrm{c}}{\mathrm{d}}}=32.79 \mathrm{d}
El resultado anterior aplica para una disminución de la tripulación, no para un aumento; como es el caso del ejercicio.
Reactivo 12
Identifique la expresión aritmética que corresponde al siguiente planteamiento.
La cuarta potencia de cinco octavos elevado a la tres.
- {\left[\left(\frac{{5}^{3}}{8}\right)\right]}^{4}
- {\left[\left(\frac{{5}^{4}}{8}\right)\right]}^{3}
- {\left[{\left(\frac{5}{8}\right)}^{3}\right]}^{4}
Solución:
Como en todo problema de convertir frases a lenguaje matemático, debemos analizar cada operación de tal forma que los operandos ocupen el lugar correcto en la expresión.
La cuarta potencia…
Establece que lo siguiente va a estar elevado a 4.
{\left[\dots \right]}^{4}
… de cinco octavos elevado a la tres.
El número que será elevado a 4 es la tercera potencia de cinco octavos. Tomamos a \frac{5}{8} , lo elevamos a 3 y este número será la base de la potencia anterior.
{\left[{\left(\frac{5}{8}\right)}^{3}\right]}^{4}
La respuesta correcta es el inciso c). El error en el inciso a) es que se eleva el numerador al segundo exponente indicado, cuando éste afecta a toda la fracción. Por otra parte, en la opción b) se cometen dos errores: intercambio de los exponentes y en la fracción solo se eleva el 5.