Guía Exani II Aritmética: 50 reactivos resueltos parte II

¡Nos vemos de nuevo aspirante! Para esta segunda parte del simulacro de Aritmética, vamos a resolver los reactivos del 31 al 40 de cara al examen de ingreso EXANI II diseñado por CENEVAL.

Ejercicios de Aritmética

Vamos con la segunda parte del simulacro de Aritmética para EXANI II. Analiza el procedimiento que has seguido para llegar a la respuesta de cada reactivo, compárala con la solución que se muestra en el simulacro e identifica posibles mejoras que acorten el tiempo.

Reactivo 31

Simplifica la siguiente expresión aplicando las propiedades de los exponentes.

{\left[\frac{{\left(\frac{1}{2}\right)}^{3}}{{\left(\frac{2}{3}\right)}^{\frac{3}{2}}}\right]}^{-2}

1. \frac{27}{312}
2. \frac{512}{27}
3. \frac{33}{97}

Solución:

Para encontrar la forma simplificada de la expresión con potencias, debemos aplicar sistemáticamente las reglas de los exponentes. Comencemos con la propiedad: potencia de un cociente.

{\left[\frac{{\left(\frac{1}{2}\right)}^{3}}{{\left(\frac{2}{3}\right)}^{\frac{3}{2}}}\right]}^{-2}=\frac{{\left[{\left(\frac{1}{2}\right)}^{3}\right]}^{-2}}{{\left[{\left(\frac{2}{3}\right)}^{\frac{3}{2}}\right]}^{-2}}

Ahora, potencia de una potencia en el numerador y denominador.

\frac{{\left[{\left(\frac{1}{2}\right)}^{3}\right]}^{-2}}{{\left[{\left(\frac{2}{3}\right)}^{\frac{3}{2}}\right]}^{-2}}=\frac{{\left(\frac{1}{2}\right)}^{3\bullet -2}}{{\left(\frac{2}{3}\right)}^{\frac{3}{2}\bullet -2}}=\frac{{\left(\frac{1}{2}\right)}^{-6}}{{\left(\frac{2}{3}\right)}^{-3}}

Vamos con la propiedad del exponente negativo.

\frac{{\left(\frac{1}{2}\right)}^{-6}}{{\left(\frac{2}{3}\right)}^{-3}}=\frac{{2}^{6}}{{\left(\frac{3}{2}\right)}^{3}}

Potencia de un cociente de nuevo en el numerador y luego doble “C”.

\frac{{2}^{6}}{{\left(\frac{3}{2}\right)}^{3}}=\frac{{2}^{6}}{\frac{{3}^{3}}{{2}^{3}}}=\frac{{2}^{3}\bullet {2}^{6}}{{3}^{3}}

Finalmente, resolvemos las potencias.

\frac{{2}^{3}\bullet {2}^{6}}{{3}^{3}}=\frac{8\bullet 64}{27}=\frac{512}{27}

{\left[\frac{{\left(\frac{1}{2}\right)}^{3}}{{\left(\frac{2}{3}\right)}^{\frac{3}{2}}}\right]}^{-2}=\frac{512}{27}

Concluimos el problema seleccionando como respuesta correcta la opción b).

Reactivo 32

Encuentre el resultado numérico de la siguiente expresión.

{\left(\sqrt{\frac{25}{36}}-\sqrt{\frac{1}{36}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{5}{4}-\frac{1}{2}\right]}^{2}

1. \frac{5}{24}
2. \frac{24}{5}
3. \frac{4}{5}

Solución:

En este caso, no solo debemos aplicar correctamente las propiedades de las potencias y los radicales, también es necesario que se respete el orden de las operaciones. Comenzamos por resolver primero lo que se encuentra dentro de los paréntesis y los corchetes.

Expresamos al 25 y 36 como potencias, desarrollamos la resta de fracciones.

{\left(\sqrt{\frac{25}{36}}-\sqrt{\frac{1}{36}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{5}{4}-\frac{1}{2}\right]}^{2}={\left(\sqrt{\frac{{5}^{2}}{{6}^{2}}}-\sqrt{\frac{1}{{6}^{2}}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{10-4}{8}\right]}^{2}

Separamos las raíces para el numerador y el denominador.

{\left(\sqrt{\frac{{5}^{2}}{{6}^{2}}}-\sqrt{\frac{1}{{6}^{2}}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{10-4}{8}\right]}^{2}={\left(\frac{\sqrt{{5}^{2}}}{\sqrt{{6}^{2}}}-\frac{1}{\sqrt{{6}^{2}}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{6}{8}\right]}^{2}

Simplificamos raíces cuadradas con potencias al cuadrado.

{\left(\frac{\sqrt{{5}^{2}}}{\sqrt{{6}^{2}}}-\frac{1}{\sqrt{{6}^{2}}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{6}{8}\right]}^{2}={\left(\frac{5}{6}-\frac{1}{6}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{3}{4}\right]}^{2}

Simplificamos las fracciones y resolvemos las potencias.

{\left(\frac{5}{6}-\frac{1}{6}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{3}{4}\right]}^{2}={\left(\frac{4}{6}\right)}^{2}÷\frac{1}{3}-2\bullet \frac{9}{16}=\frac{16}{36}÷\frac{1}{3}-2\bullet \frac{9}{16}

\frac{16}{36}÷\frac{1}{3}-2\bullet \frac{9}{16}=\frac{4}{9}÷\frac{1}{3}-\frac{9}{8}=\frac{4}{3}-\frac{9}{8}=\frac{5}{24}

Finalmente:

{\left(\sqrt{\frac{25}{36}}-\sqrt{\frac{1}{36}}\right)}^{2}÷\frac{1}{3}-2{\left[\frac{5}{4}-\frac{1}{2}\right]}^{2}=\frac{5}{24}

Comparando el resultado con las opciones, escogemos como correcta la a).

Reactivo 33

Dado el siguiente procedimiento, identifique el o los pasos en los que se ha cometido un error aplicando jerarquía de operaciones.

Expresión.

\left\{\left[\left(5-6\right)+\left(7-3\right)-2\right]+1\right\}-3

1. \left\{\left[\left(5-6\right)+\left(7-3\right)-2\right]+1\right\}-3=\left\{\left[\left(5-6\right)+\left(7-3\right)-2\right]-2\right\}
2. \left\{\left[\left(5-6\right)+\left(7-3\right)-2\right]-2\right\}=\left\{\left[\left(-1\right)+\left(4\right)-2\right]-2\right\}
3. \left\{\left[\left(-1\right)+\left(4\right)-2\right]-2\right\}=\left\{\left[1\right]-2\right\}
4. \left\{\left[1\right]-2\right\}=-1

 

1. Paso 2
2. Paso 3 y 4
3. Paso 1

Solución:

Como es costumbre en este tipo de problemas, debemos desarrollar paso a paso el ejercicio aplicando correctamente las propiedades de los signos y la jerarquía de operaciones. Comenzamos por las llaves, dentro de ellas hay unos corchetes y dentro de los corchetes paréntesis. La regla dice que vamos de adentro hacia afuera eliminando paréntesis, luego corchetes y por último llaves.

\left\{\left[\left(5-6\right)+\left(7-3\right)-2\right]+1\right\}-3=\left\{\left[\left(-1\right)+\left(4\right)-2\right]+1\right\}-3

Aquí identificamos el primer error, en el paso 1 se realiza la resta entre el 3 fuera de las llaves con el 1 dentro de ellas. Continuamos resolviendo dentro de los corchetes.

\left\{\left[\left(-1\right)+\left(4\right)-2\right]+1\right\}-3=\left\{1+1\right\}-3

Vamos con el interior simplificado de las llaves

\left\{1+1\right\}-3=2-3=-1

Aunque el resultado es el mismo, en el enunciado se ha cometido un claro error en el paso 1. Finalizamos el ejercicio seleccionando como respuesta correcta la opción c).

Reactivo 34

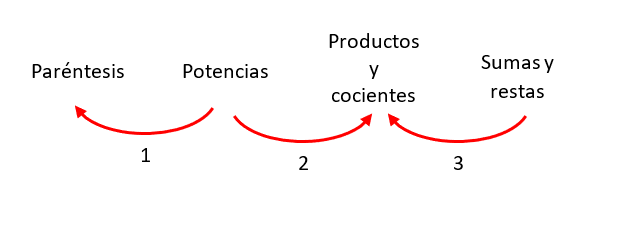
¿A cuáles de las flechas en la siguiente imagen cambiarías de sentido para respetar correctamente el orden de las operaciones?

1. 1
2. 1 y 3
3. 2

Solución:

Las reglas de jerarquía de operaciones son simples y claras a la hora de establecer que se realiza primero en una expresión que combina, sumas, productos y potencias. Sabemos de la teoría que:

1. Paréntesis
2. Potencias y radicales
3. Productos y cocientes, de izquierda a derecha
4. Sumas y restas, de izquierda a derecha

Donde el número indica el orden, primero se resuelve el interior de los paréntesis, luego las potencias, seguido de productos y cocientes, hasta culminar con sumas y restas. Teniendo en cuenta todo lo anterior, debemos cambiar la orientación de las flechas 1 y 3.

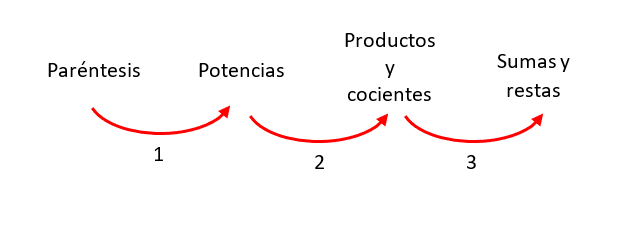
Concluimos indicando como respuesta correcta la opción b).

Reactivo 35

Resuelve siguiendo las reglas de jerarquía de operaciones.

3\times \{\sqrt{(5-2)\times (7-4)}-(5-3)+(8-3)-[6-(7-2)+8]-6\}

1. -27
2. 27
3. 4

Solución:

La regla en el caso de signos de agrupación nos dice que: primero se resuelve el interior de las llaves, si dentro de ellas hay corchetes se inicia por ellos y si dentro de estos últimos hay paréntesis, se resuelve el interior de los paréntesis. Es un procedimiento de adentro hacia afuera.

3\times \left\{\sqrt{\left(5-2\right)\times \left(7-4\right)}-\left(5-3\right)+\left(8-3\right)-\left[6-\left(7-2\right)+8\right]-6\right\}

Dentro de las llaves hay corchetes y en ellos paréntesis, comenzamos por ellos.

=3\times \left\{\sqrt{\left(5-2\right)\times \left(7-4\right)}-\left(5-3\right)+\left(8-3\right)-\left[6-5+8\right]-6\right\}

=3\times \left\{\sqrt{\left(5-2\right)\times \left(7-4\right)}-\left(5-3\right)+\left(8-3\right)-9-6\right\}

Ahora, vamos con los paréntesis dentro de las llaves.

=3\times \left\{\sqrt{\left(5-2\right)\times \left(7-4\right)}-2+5-9-6\right\}

Continuamos con la raíz, dentro de ella hay dos paréntesis, resolvemos su interior.

=3\times \left\{\sqrt{3\times 3}-2+5-9-6\right\}

Expresamos a 3\times 3 como {3}^{2} .

=3\times \left\{\sqrt{{3}^{2}}-2+5-9-6\right\}=3\times \left\{{3}^{2/2}-2+5-9-6\right\}=3\times \left\{3-2+5-9-6\right\}

Resolvemos las sumas y restas de izquierda a derecha.

=3\times \left\{1+5-9-6\right\}=3\times \left\{6-9-6\right\}=3\times \left\{-3-6\right\}=3\times -9=-27

Finalmente:

3\times \left\{\sqrt{\left(5-2\right)\times \left(7-4\right)}-\left(5-3\right)+\left(8-3\right)-\left[6-\left(7-2\right)+8\right]-6\right\}=-27

Concluimos indicando como respuesta correcta la opción a).

Reactivo 36

Coloque los signos de agrupación necesarios para que se cumpla la igualdad.

3+5\times 4-(8+4)÷2=26

1. \left[\left(3+5\right)\times 4-\left(8+4\right)\right]÷2
2. \left(3+5\right)\times 4-\left(8+4\right)÷2
3. 3+\left[5\times 4-\left(8+4\right)\right]÷2

Solución:

Si evaluamos la expresión tal como se encuentra escrita, obtendremos el siguiente resultado:

3+5\times 4-\left(8+4\right)÷2=3+5\times 4-12÷2=3+20-6=17

Si pensamos un poco, lo natural sería intentar colocar paréntesis que encierran al 3 y al 5, de esa manera, el número equivalente que multiplica al 4 sería mayor.

\left(3+5\right)\times 4-\left(8+4\right)÷2=8\times 4-12÷2

8\times 4-12÷2=32-6=26

En efecto, concluimos que los paréntesis se deben colocar encerrando al 3 y al 5 para que el resultado sea 26. Comparando con las opciones, indicamos como correcta la b).

Reactivo 37

Encuentre el resultado de simplificar la siguiente operación.

\frac{\left(1+{2}^{3}÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{112}÷4\right)}

1. \frac{1}{8}
2. 1/\sqrt{7}
3. \frac{1}{4}

Solución:

Iniciamos resolviendo el interior de los paréntesis tanto en el numerador como en el denominador. Siguiendo el orden de las operaciones, vamos primero con los cocientes y, en ellos, con la potencia {2}^{3} en el numerador y con el radical \sqrt{112} en el denominador.

\frac{\left(1+{2}^{3}÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{112}÷4\right)}=\frac{\left(1+8÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{7\times 16}÷4\right)}

El 112 no tiene raíz cuadrada exacta, pero puede factorizarse como 7\times 16 y el 16 sí que tiene raíz cuadrada exacta. Aplicamos la propiedad de la raíz del producto.

\frac{\left(1+8÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{7\times 16}÷4\right)}=\frac{\left(1+8÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{7}\sqrt{16}÷4\right)}

=\frac{\left(1+8÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+4\sqrt{7}÷4\right)}

El {4}^{0} es igual a 1 porque todo número elevado a cero es 1. Por otra parte, 4\sqrt{7}÷4 es igual a \sqrt{7} porque el 4 del dividendo se simplifica con el 4 del divisor.

=\frac{\left(1+8÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left(1+\sqrt{7}\right)}

Resolvemos el interior del paréntesis del numerador.

=\frac{\left(1+2\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left(1+\sqrt{7}\right)}=\frac{3+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left(1+\sqrt{7}\right)}

En el denominador ya no es posible seguir simplificando. En el numerador, vamos con el cociente \sqrt{63}÷3 , donde el 63 puede escribirse como 7\times 9 .

\frac{3+\sqrt{28}-\sqrt{7\times 9}÷3-2}{4\times \left(1+\sqrt{7}\right)}=\frac{3+\sqrt{28}-\sqrt{7}\sqrt{9}÷3-2}{4\times \left(1+\sqrt{7}\right)}

=\frac{3+\sqrt{28}-3\sqrt{7}÷3-2}{4\times \left(1+\sqrt{7}\right)}

Nuevamente, el 3 del dividendo se simplifica con el 3 del divisor.

\frac{3+\sqrt{28}-3\sqrt{7}÷3-2}{4\times \left(1+\sqrt{7}\right)}=\frac{3+\sqrt{28}-\sqrt{7}-2}{4\times \left(1+\sqrt{7}\right)}

El 28 del radical se puede escribir como 4\times 7 .

\frac{3+\sqrt{4\times 7}-\sqrt{7}-2}{4\times \left(1+\sqrt{7}\right)}=\frac{3+2\sqrt{7}-\sqrt{7}-2}{4\times \left(1+\sqrt{7}\right)}

Podemos restar al 3 con el 2 y a 2\sqrt{7} con \sqrt{7} .

=\frac{1+\sqrt{7}}{4\times \left(1+\sqrt{7}\right)}

El 1+\sqrt{7} del numerador se simplifica con el del denominador.

\frac{1+\sqrt{7}}{4\times \left(1+\sqrt{7}\right)}=\frac{1}{4}

Finalmente:

\frac{\left(1+{2}^{3}÷4\right)+\sqrt{28}-\sqrt{63}÷3-2}{4\times \left({4}^{0}+\sqrt{112}÷4\right)}=\frac{1}{4}

Concluimos indicando que la respuesta correcta es la opción c).

Reactivo 38

Relacione la expresión en notación científica con su expansión correspondiente.

1. 1a, 2c, 3b
2. 1b, 2a, 3c
3. 1c, 2a, 3b

Solución:

La notación científica es una forma de expresión exponencial en base 10 que nos permite expresar de forma compacta cantidades grandes y pequeñas. Consiste en la idea básica de la división o multiplicación por un 1 seguido de cierta cantidad de ceros.

\mathrm{5,200,000}=5.2\times {10}^{6}

Cuando se nos pide expandir una cantidad en notación científica, debemos devolver la cantidad a su expresión original, sea como un decimal chico o como un número grande. Iremos expandiendo cada ítem de la columna izquierda para asociarlo con una cantidad en la columna derecha.

Primera cantidad.

2\times {10}^{-3}

El {10}^{-3} se puede escribir como:

2\times \frac{1}{{10}^{3}}=\frac{2}{{10}^{3}} =\frac{2}{1000}

Corremos la coma hacia la izquierda como tantos ceros hay en el denominador.

\frac{2}{1000}=0.002

Comparando con la columna derecha: 1b.

Segunda cantidad.

{\left(3\times {10}^{-2}\right)}^{-2}\times 27

Aplicamos potencia de una potencia.

\left({3}^{-2}\times {10}^{-2\bullet -2}\right)\times 27=27\bullet \frac{1}{9}\times {10}^{4}\times 27

Simplificamos el 27 con el 9 y expandimos.

\frac{1}{9}\times {10}^{4}\times 27=3\times {10}^{4}=30000

Comparando indicamos: 2a.

Tercera cantidad.

\frac{9\times {10}^{6}}{3\times {\left({10}^{3}\right)}^{2}}

Deshacemos en el denominador la potencia de una potencia.

\frac{9\times {10}^{6}}{3\times {\left({10}^{3}\right)}^{2}}=\frac{9\times {10}^{6}}{3\times {10}^{6}}

Simplificamos las potencias de base 10.

\frac{9\times {10}^{6}}{3\times {10}^{6}}=\frac{9}{3}\times {10}^{6-6}=\frac{9}{3}=3

Finalmente: 3c.

Uniendo todas las respuestas nos queda: 1b, 2a, 3c. Comparando con las opciones, indicamos la b) como correcta.

Reactivo 39

Complete correctamente la siguiente frase:

Si a y b son dos números enteros, diremos que a es ______ de b si el primero contiene un número entero de veces a b .

1. Múltiplo
2. Divisor
3. Sustraendo

Solución:

Primero analizaremos la segunda parte de la frase para comprender el contexto.

…si el primero contiene un número entero de veces a b .

Cuando dice “el primero” se refiere a la cantidad a , la cuál es entera al igual que b . Supongamos que le damos valores a a y b , por ejemplo: 10 y 2. En este caso, si sumamos el 2 cinco veces seguidas obtenemos 10.

10=2+2+2+2+2=5\bullet 2

Decimos entonces que el 10 contiene cinco veces al 2.

Lo anterior descrito con un sencillo ejemplo es lo que se conoce en teoría de números como múltiplo, donde el 10 es un múltiplo de 2. En base a esto, completamos la frase como:

Si a y b son dos números enteros, diremos que a es múltiplo de b si el primero contiene un número entero de veces a b .

Comparando con las opciones, seleccionamos como correcta la a).

Reactivo 40

Un número es divisible entre 6 si:

1. Es divisible entre 2
2. Es divisible entre 3
3. Es divisible entre 2 y 3

 

1. 3
2. 1
3. 2

Solución:

El criterio de divisibilidad del 6 está compuesto por los criterios de divisibilidad de sus submúltiplos, en este caso: el 2 y el 3, por tanto:

Todo número es divisible entre 6 si es divisible por 2 y por 3 a la vez.

Concluimos entonces que la respuesta correcta es la opción 3 o el inciso a).