Ejercicios Examen IPN | Parte 3 Competencia Lectora

Vamos por la parte número 3 de la solución de los ejercicios de competencia lectora para el examen de ingreso al IPN, ahora vamos con los reactivos del 21 al 30.

Antes de avanzar, te recordamos que debes prestar la máxima atención en cada uno de los reactivos. Solamente así podrás entender bien cómo se resuelven. ¡Empecemos!

Lee el siguiente texto y responde los reactivos del 21 al 30.

LAS PARADOJAS MATEMÁTICAS MÁS FAMOSAS

[1] Los seres humanos tenemos la necesidad de llegar a conclusiones lógicas a partir de razonamientos que sabemos que son válidos, pero hay veces en las que, ya sea de forma real o hipotética, la lógica no funciona como esperamos y entramos de lleno en la formulación de paradojas porque nuestra mente no es capaz de encontrar el razonamiento de una conclusión compleja, incluso sabiendo que hemos realizado la argumentación correcta. Pasa lo mismo en el terreno de las matemáticas, que pese a que son perfectamente lógicas nos hacen llegar a conclusiones que se escapan totalmente de lo que nosotros consideramos racional. Veamos algunos ejemplos:

[2] Paradoja de Möbius: Es de carácter visual. Se trata de una figura matemática imposible desde nuestra perspectiva tridimensional de una banda plegada con una superficie de una sola cara y un solo borde, por lo que no cuadra con nuestra distribución mental de los elementos.

[3] Paradoja del hotel infinito: Imaginemos que queremos construir el hotel más grande del mundo. Al principio, pensamos en hacer uno de 1.000, 20.000, 500.000 o 1.000.000 habitaciones, pero es posible que alguien lo supere. Por ello, llegamos a la conclusión de que lo mejor es construir uno con habitaciones infinitas. El problema es que en un hotel infinito que se llena de infinitos huéspedes, las matemáticas nos dicen que quedaría abarrotado. Esta paradoja expone que para solucionar este problema, cada vez que entre un nuevo huésped, los que ya estaban antes tienen que desplazarse a la siguiente habitación, es decir, sumar 1 a su número de habitación actual. De este modo, se resuelve el problema ya que cada nuevo huésped se hospedará en la habitación número 1 del hotel.

[4] Paradoja de Russell: Está relacionada con la teoría de conjuntos y expone que en X lugar, todos los hombres tienen que ir afeitados, pero solo hay un barbero. Con el fin de no saturarlo, se establece que el barbero solo puede afeitar a aquellas personas que no puedan hacerlo por sí solas. La paradoja se establece cuando el barbero se afeite porque estará demostrando que puede afeitarse por sí solo, pero entonces estará rompiendo con la norma, pero si no se afeita, romperá también con la norma de ir afeitado, entonces, ¿qué es lo que tiene que hacer el barbero?

Fragmento adaptado de Beltrán, P. (2020). Las 10 paradojas matemáticas y físicas más famosas. Médico Plus. Recuperado de: https://medicoplus.com/ciencia/paradojas-matematicas-fisicas

Reactivo 21

Relacionar la columna de estructura con el contenido del texto.

Estructura	Contenido
1. Introducción 2. Desarrollo 3. Conclusión	A. La forma estricta en la que el ser humano concibe la lógica es falible. B. El ser humano es sumamente racional. C. Algunas paradojas

1. 1A, 2B, 3C
2. 1B, 2C, 3A
3. 1A, 2C, 3B
4. 1B, 2A, 3C

Solución

En este primer ejercicio debemos quedarnos con la opción c). Para explicarlo bien vamos a abordar cada parte de la estructura por separado.

Introducción

Recordemos que la introducción es la parte del texto que sirve de entrada al contenido. En el caso de la lectura, la introducción corresponde a la siguiente sección del inicio:

• “Los seres humanos tenemos la necesidad de llegar a conclusiones lógicas […], pero hay veces en las que, ya sea de forma real o hipotética, la lógica no funciona como esperamos y entramos de lleno en la formulación de paradojas porque nuestra mente no es capaz de encontrar el razonamiento de una conclusión compleja” (resaltamos con negritas la parte más importante).

Lo que leemos allí es, en resumen, que la lógica no siempre funciona como nosotros la entendemos y que, por lo tanto, nuestro cerebro no llega a entender todas las ideas. Por ende, nuestra forma de comprender la lógica es falible, o sea, puede fallar.

Ahora bien, ¿por qué lo anterior corresponde a la introducción? Pues porque nos presenta la idea que se va a desarrollar luego; nos pone en contexto para entender el resto de la lectura.

Desarrollo

El desarrollo es la parte del texto en la que se amplía la idea que vimos en la introducción. Es decir, se profundiza en ella, ya sea explicando o brindando ejemplos al respecto.

Partiendo de lo anterior, es natural pensar que las paradojas representan el desarrollo, puesto que ellas son una muestra de casos en los que nuestra forma de entender la lógica falla. De esa forma, cada paradoja extiende o desarrolla dicha idea.

Conclusión

Por su parte, la conclusión se refiere a la idea que cierra el contenido de la lectura. Pudiéramos pensar que se encontraría al final, aunque no siempre es así. De hecho, en el texto que estamos estudiando se halla en la última parte del primer párrafo:

• “Pasa lo mismo en el terreno de las matemáticas, que pese a que son perfectamente lógicas nos hacen llegar a conclusiones que se escapan totalmente de lo que nosotros consideramos racional”.

La parte en negritas nos deja en claro algo: el ser humano es racional. Esa es la conclusión a la que podemos llegar luego de fijarnos en la introducción y en el desarrollo.

 

Tal como podemos observar, la forma estricta en la que el ser humano concibe la lógica es falible corresponde a la introducción; las paradojas pertenecen al desarrollo; y el hecho de que el ser humano es racional representa la conclusión.

Así, la unión correcta es 1A, 2C y 3B, como se indica en la opción c). Por lo tanto, esa es la correcta.

Reactivo 22

Los párrafos ____ y ____ presentan una relación de información _________ mayoritariamente.

1. 1 – 2 – explicativa
2. 2 – 3 – explicativa
3. 1 – 3 – ejemplificativa
4. 2 – 3 – ejemplificativa

Solución

Para solucionar este ejercicio debemos optar por la b), dado que los párrafos 2 y 3 plantean una información explicativa.

Si bien las paradojas mencionadas en cada uno de esos párrafos son, en cierto sentido, un ejemplo de la introducción del texto, el contenido de ellos nos define las paradojas en sí. Dicho de otra manera, nos explica en qué consisten. En consecuencia, la información que contienen es de tipo explicativa, lo cual demuestra que hemos escogido bien.

Reactivo 23

De las siguientes opciones, ¿cuál podría ser una idea secundaria del texto anterior?

1. Otra paradoja, como la del cumpleaños
2. El nombre del lugar en donde vive el barbero
3. El número exacto de las habitaciones del hotel
4. August Moebius construyó la cinta con su nombre

Solución

Sin lugar a dudas, la opción a elegir aquí es la a). Antes que nada, recordemos que una idea secundaria es aquella refuerza o ejemplifica la idea principal. Esta última, en el texto, es que nuestra forma de entender la lógica puede fallar.

Ahora debemos identificar cuáles son las ideas secundarias que ya están en el texto. Claramente, esas ideas son las paradojas. ¿Por qué? Porque ellas, al ser ejemplos de casos en los que fallamos con la lógica, desarrollan y refuerzan la idea principal del texto.

Si las paradojas son ideas secundarias, está claro que otra paradoja —en este caso, la del cumpleaños— también sería una idea de ese tipo. Esa es la razón por la que debemos escoger la opción a).

Ninguna otra de las opciones serviría para resolver el ejercicio. Esto se debe a que no funcionan como ideas secundarias, porque no refuerzan la idea principal del texto.

Reactivo 24

El texto anterior puede clasificarse como ________ debido a que es ________ y su finalidad es ________ a los lectores.

1. formal – neutral – educar
2. formal – ecuánime -capacitar
3. expositivo – objetivo – informar
4. expositivo – formal – convencer

Solución

Este ejercicio se resuelve seleccionando la opción c). Si la usamos para completar el texto, obtenemos el resultado siguiente:

• “El texto anterior puede clasificarse como expositivo debido a que es objetivo y su finalidad es informar a los lectores”.

¿Por qué cada una de las palabras que completan el texto es correcta? A continuación te lo explicamos:

• El texto es expositivo debido a que se centra en transmitir una información. Su objetivo es plantear un tema para ser recibido por el lector.
• El texto es objetivo porque el autor en ninguna parte emite un juicio o una crítica sobre lo que nos está contando. Simplemente, se limita a mostrarnos la información.
• La finalidad el texto es informar debido a que intenta transmitir un tema. No busaca convencer ni educar la forma de pensar del lector, sino hacer que conozca un asunto en particular.

Si escogiéramos cualquier otra combinación, las características serían diferentes y no se ajustarían al texto que hemos leído. Por tanto, solo la c) resuelve el reactivo.

Reactivo 25

¿Qué idea sintetiza lo expuesto en el párrafo [4]?

1. El barbero está estresado siempre
2. El barbero siempre va a romper la ley
3. La teoría de conjuntos es contradictoria
4. El local del barbero siempre estaba saturado

Solución

En este caso debemos quedarnos con la opción c). Tengamos en cuenta que el ejercicio nos pide identificar la idea que resuma lo que se expone en el párrafo 4, dentro del cual se explica la paradoja de Russell.

Lo que se plantea en el párrafo es la imposibilidad del barbero de afeitarse a sí mismo sin romper la norma de afeitar únicamente a quienes no saben. De ese modo, la teoría de conjunto entra en una contradicción.

Tenemos, entonces, que la teoría de conjuntos es contradictoria. Esa idea sintetiza todo lo expresado en el párrafo [4], ya que todo lo que se expone en él sirve para dar a entender ese punto.

Reactivo 26

Seleccionar la figura que es compatible con el párrafo [2].

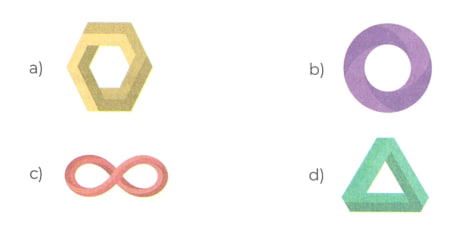
Solución

Esta vez debemos optar por la c) una vez más. En dicha opción aparece la única imagen que encaja con las características que se indican en la paradoja del párrafo [2]. Se trata de una banda con un único borde y una sola cara, los cuales hacen que la banda en sí no se ajuste a nuestra perspectiva tridimensional.

Reactivo 27

¿Cuál de las siguientes ideas es compatible con el párrafo [3] del texto anterior?

1. Lo expuesto en el párrafo explica muy claramente que hay infinitos dentro de un infinito.
2. Está demostrado que la imaginación y creatividad del ser humano no tiene ni tendrá límites.
3. Todas las paradojas han sido formuladas para solucionar exitosa y definitivamente problemas muy complejos.
4. En un hotel con infinitas habitaciones solo es posible hospedar a infinitos huéspedes si estos entran en la habitación número 1.

Solución

Para responder este reactivo tenemos que quedarnos con la opción d). Para entenderlo debemos fijarnos en un fragmento del párrafo [3]:

• “[…] en un hotel infinito que se llena de infinitos huéspedes, las matemáticas nos dicen que quedaría abarrotado. […] para solucionar este problema, cada vez que entre un nuevo huésped, los que ya estaban antes tienen que desplazarse a la siguiente habitación, es decir, sumar 1 a su número de habitación actual. De este modo, se resuelve el problema ya que cada nuevo huésped se hospedará en la habitación número 1 del hotel”.

Lo que leemos ahí es la solución al problema del hotel con huéspedes y habitaciones infinitos, la cual consiste en que cada nuevo huésped se hospede en la habitación número 1. Precisamente de eso nos habla la opción d).

Ninguna otra opción se puede sostener con lo que dice el párrafo [3]. Por lo tanto, la d) es la única compatible con él.

Reactivo 28

¿Qué puede deducirse del texto anterior?

1. La distribución mental de elementos de los seres humanos es tridimensional
2. Nuestra mente es capaz de encontrar el razonamiento de una conclusión compleja
3. El adaptar conceptos complejos al plano físico es la mejor manera de aclararlos
4. Los problemas sociales y de organización pueden resolverse a través de paradojas

Solución

La opción correcta dentro de este ejercicio no es otra que la a). Luego de leer el texto anterior somos capaces de entender que nuestra distribución mental de los elementos es tridimensional. A esta conclusión podemos llegar luego de leer detenidamente el párrafo [2]:

• “Paradoja de Möbius: […]. Se trata de una figura matemática imposible desde nuestra perspectiva tridimensional de una banda plegada con una superficie de una sola cara y un solo borde, por lo que no cuadra con nuestra distribución mental de los elementos”.

Si juntamos las dos partes en negritas lo que entendemos es que la distribución mental es de tipo tridimensional. Esta es la única idea de todas las que aparecen en las opciones que se puede deducir del texto, por lo cual debemos quedarnos con la a).

Reactivo 29

Seleccionar la idea que representa la conclusión del texto anterior.

1. Las matemáticas siempre se valen de las paradojas para poder resolver problemas complejos y así simplificarlos lo más posible
2. Las paradojas se limitan al campo de las matemáticas ya que es ahí en donde más se presentan debido a la complejidad de sus ramas de estudio
3. Todos los grandes matemáticos han creado y desarrollado diversas paradojas de las áreas de las matemáticas en las que se hayan especializado
4. Las paradojas representan la complejidad conceptual de un campo específico del saber porque su explicación no concuerda con el modo tradicional del pensamiento

Solución

Aquí la opción a elegir es la d).

Las paradojas son una representación o ejemplo de las dificultades que podemos hallar en una rama del conocimiento. ¿Pero por qué? Porque al momento de explicarlas nos damos cuenta de que no se ajustan a la forma como pensamos.

En consecuencia, las paradojas demuestran que la complejidad conceptual de una disciplina puede ir más allá de nuestra comprensión.

Reactivo 30

¿Cuál es la conclusión del párrafo [3]?

1. Lo mejor es construir un hotel con habitaciones infinitas
2. Si existieran hoteles infinitos, siempre estarían llenos de infinitos huéspedes
3. El concepto de infinito aún no se ha desarrollado ni comprendido en su totalidad
4. En el hotel nunca habrá una última habitación, ya que siempre se puede añadir una más

Solución

Este último ejercicio se resuelve seleccionando la d).

La conclusión del párrafo [3] es que el hotel jamás tendrá una última habitación, puesto que se añadirá una más siempre que llegue otro huésped: “… cada vez que entre un nuevo huésped, los que ya estaban antes tienen que desplazarse a la siguiente habitación, es decir, sumar 1 a su número de habitación actual”.

Por ende, no hay posibilidad de que se alcance un número máximo de habitaciones, dado que no hay un límite de huéspedes. Basándonos en ello, podemos decir que la d) es la opción correcta.