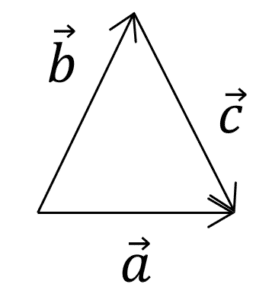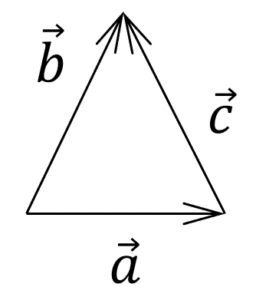¡Hola, aspirante! Encuentra la solución guiada de los 30 reactivos de física para el área de Ciencias Médico Biológicas de la guía, para el examen de ingreso al Instituto Politécnico Nacional.

La guía ha sido dividida en tres partes para que puedas establecer las pausas correspondientes entre cada bloque de estudio. Recuerda que el descanso también forma parte de tu proceso de aprendizaje.
A continuación, tienes un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
La estructura del examen al IPN 2023 ha sido modificada. Ahora, el total de reactivos por materia cambia en función al área de conocimientos. Las carreras que ofrece el Instituto Politécnico Nacional se dividen en 3 grandes áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
El grado de dificultad dependerá del nivel de preparación que tengas para el examen. Concéntrate en estudiar muy bien los puntos que vienen en el temario para cada materia y no dejes de practicar para dominar los temas con facilidad. Sobre todo, apóyate en las soluciones guiadas y simulacros de la prueba.
Este año se adicionaron dos nuevos temas: historia e inglés (reading comprehension), aumentando así la cantidad de reactivos a 140. La guía de física para el área de Ciencias Médico Biológicas, incluyen reactivos de física I y II del nivel medio superior del IPN.
Temario de física del área CMB IPN
Estos son los temas de física que deberás estudiar antes de presentar el examen:
- Física para CMB
- Sistemas de unidades y mediciones
- Álgebra vectorial
- Cinemática y dinámica
- Estática
- Propiedades generales de la materia
- Mecánica de fluidos
- Termodinámica
- Acústica
- Electricidad
- Electromagnetismo
- Electroinducción y ondas electromagnéticas
- Óptica
¿Cómo resolver la guía del IPN?
La dinámica es sencilla, los ejercicios que vienen en la guía son un adelanto de lo que puede salir en el examen. Por ello, lo primero que debes hacer es familiarizarte muy bien con los puntos de física que específica el temario, consultar la bibliografía recomendada en la guía e ir paso a paso resolviendo los ejercicios con nuestra ayuda hasta que los domines por completo.
No comiences a resolver sin tener una idea de los temas que saldrán.
Es normal querer ir rápido para terminar la guía lo más pronto posible, pero rapidez rara vez implica calidad. El proceso de aprendizaje necesita tiempo, que reflexiones acerca de los temas y que los comprendas desde tu perspectiva.
Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
- Física no se trata de aplicar fórmulas. Debes conocer los fundamentos, analizar los enunciados y seleccionar las leyes correctas para resolver el problema.
Reactivo 1
Un error de un ___ incurrido en la medida de una longitud de algunos centímetros es inaceptable; sin embargo, el mismo error al medir la distancia entre ___ puntos de una carretera en la que distan varios kilómetros, carece de importancia.
- centímetro – 2
- centímetro – 3
- milímetro – 2
- milímetro – 3
Solución:
Para completar de forma correcta a la frase del enunciado, debemos tener presente los conceptos asociados a la medida e instrumentos de medición.
Los errores en las mediciones indican la diferencia que existe entre la medición y el valor que tomamos como real de una magnitud. En una medición hecha en centímetros, un error expresado en milímetros representa un pequeño porcentaje de la medición.
Por otro lado, cuando en el mismo contexto el error está expresado unidades o decenas centímetros, el error pasa a ser diez veces mayor respecto al anterior. En las mediciones queremos que la incertidumbre sea lo más pequeña posible, por tanto, un error de centímetros sería inaceptable.
Ahora, teniendo en cuenta que tomamos el mismo instrumento graduado en centímetros para medir la longitud entre dos puntos que distan kilómetros, un error de algunos centímetros en este contexto es despreciable. Recordemos que un kilómetro equivale a 100,000 centímetros, que porcentualmente sería un valor aproximadamente de 0.02%.
Teniendo en cuenta el análisis anterior, concluimos que el inciso que completa de forma correcta al enunciado es el a).
Un error de un centímetro incurrido en la medida de una longitud de algunos centímetros es inaceptable; sin embargo, el mismo error al medir la distancia entre 2 puntos de una carretera en la que distan varios kilómetros, carece de importancia.
Reactivo 2
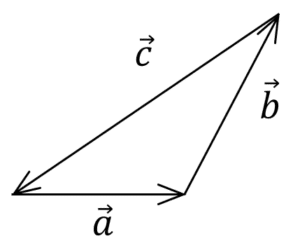
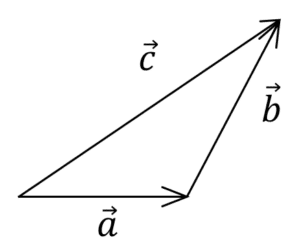
Los vectores \overrightarrow{a},\overrightarrow{b}\text{ у }\overrightarrow{c} están relacionados por \overrightarrow{c}=\overrightarrow{b}-\overrightarrow{a} . ¿Qué figura muestra esta relación?
Solución:
Este problema se resuelve rápidamente si conoces la teoría detrás de las operaciones básicas entre vectores. Para dar contexto a la respuesta, vamos a explicar brevemente cómo se construye el vector resta entre \overrightarrow{a} y \overrightarrow{b} .
Supongamos que tenemos a dos vectores \overrightarrow{a} y \overrightarrow{b} cualesquiera en el plano.
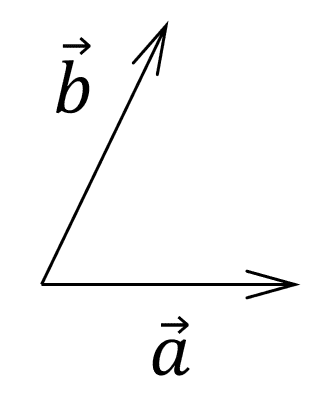
\overrightarrow{c}=\overrightarrow{b}-\overrightarrow{a}
Iniciamos encontrando al vector opuesto -\overrightarrow{a} para convertir a la resta en una suma de vectores.
\overrightarrow{c}=\overrightarrow{b}+\left(-\overrightarrow{a}\right)
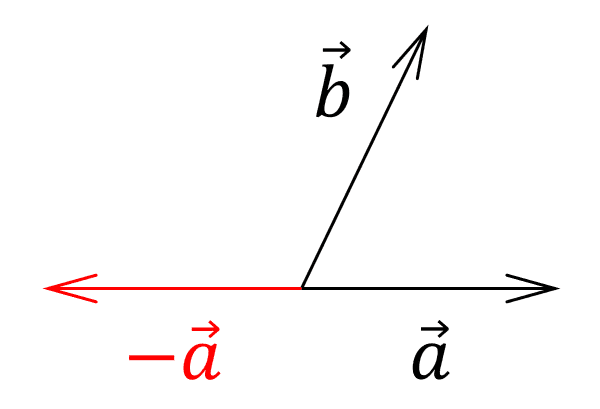
Esta suma se resuelve gráficamente mediante el método del paralelogramo.
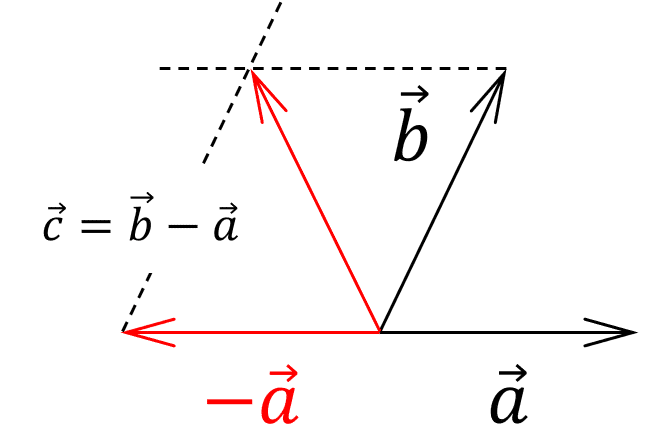
Trasladamos al vector \overrightarrow{c} .
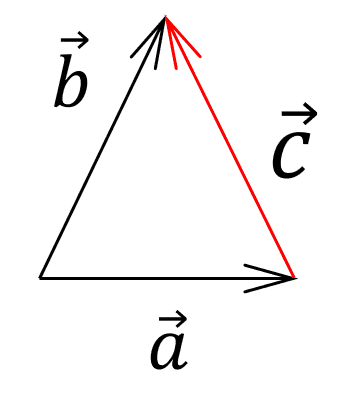
Con esta imagen llegamos a una conclusión importante: el vector resta tiene su origen en el sustraendo ( \overrightarrow{a} ) y su extremo en el minuendo ( \overrightarrow{b} ). Indicamos como respuesta correcta es el inciso d).
Reactivo 3
Calcular la velocidad en m/s, de un ciclista que corre en una pista a 85 km/h.
- 12.05\mathrm{m}/\mathrm{s}
- 16.66\mathrm{m}/\mathrm{s}
- 23.61\mathrm{m}/\mathrm{s}
- 36.80\mathrm{m}/\mathrm{s}
Solución:
En este problema, debemos aplicar la transformación de unidades. Debemos recordar que 1 hora tiene 3600 segundos y que 1 kilómetro tiene 1000 metros. Transformamos las unidades de la siguiente forma:
85\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}\cdot \frac{1000 \mathrm{m}}{1 \mathrm{k}\mathrm{m}}=\frac{\left(85 \mathrm{k}\mathrm{m}\right)\left(1 \mathrm{h}\right)\left(1000 \mathrm{m}\right)}{\left(1 \mathrm{h}\right)\left(3600 \mathrm{s}\right)\left(1 \mathrm{k}\mathrm{m}\right)}=23.61 \mathrm{m}/\mathrm{s}
El ciclista corre a una velocidad de 23.61 \mathrm{m}/\mathrm{s} .
La respuesta correcta es el inciso c). En la guía hay un error al indicar cuál es la respuesta correcta.
Reactivo 4
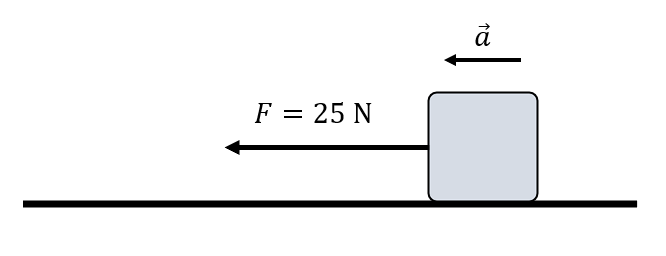
Calcular la aceleración de un cuerpo de 50 kg que es jalado sobre una mesa horizontal sin rozamiento por una cuerda que se mantiene horizontal a la superficie y a la cual se le imprime una fuerza de 25 N.
- 0.5\mathrm{m}/{\mathrm{s}}^{2}
- 1.0\mathrm{m}/{\mathrm{s}}^{2}
- 2\mathrm{m}/{\mathrm{s}}^{2}
- 2.5\mathrm{m}/{\mathrm{s}}^{2}
Solución:
Examinando los datos que nos suministra el enunciado, debemos aplicar la segunda ley de Newton para calcular la aceleración del cuerpo. Debido a que no hay rozamiento, la fuerza neta que actúa sobre el cuerpo es la de 25 N.
F=ma
Despejamos el módulo de la aceleración a partir de la ecuación anterior.
a=\frac{F}{m}=\frac{25}{50}=0.5 \mathrm{m}/{\mathrm{s}}^{2}
La aceleración del cuerpo es igual a 0.5 \mathrm{m}/{\mathrm{s}}^{2} .
Indicamos al inciso a) como la respuesta correcta. En la guía del IPN hay un error al indicar cuál es la respuesta correcta. Parece ser que el cociente lo hicieron al revés \frac{50}{25} .
Reactivo 5
Ordenar en forma ascendente la magnitud de aceleración del movimiento de los siguientes cuerpos.
- Un cuerpo de 40 kg al que se le aplica una fuerza de 100 N.
- Un cuerpo de 90 kg al que se le aplica una fuerza de 140 N.
- Un cuerpo de 18 kg al que se le aplica una fuerza de 30 N.
- Un cuerpo de 40 kg al que se le aplica una fuerza de 25 N.
- 4, 2, 3, 1
- 2, 4, 1, 3
- 4, 1, 3, 2
- 2, 3, 1, 4
Solución:
Debemos calcular el módulo de la aceleración en cada inciso, para luego compararlas entre ellas y ordenarlas de forma ascendente. Debemos emplear en todos los casos la segunda ley de Newton:
F=ma
Aceleración del primer cuerpo.
{a}_{1}=\frac{{F}_{1}}{{m}_{1}}=\frac{100}{40}=2.5 \mathrm{m}/{\mathrm{s}}^{2}
Aceleración del segundo cuerpo.
{a}_{2}=\frac{{F}_{2}}{{m}_{2}}=\frac{140}{90}=1.55 \mathrm{m}/{\mathrm{s}}^{2}
Aceleración del tercer cuerpo.
{a}_{3}=\frac{{F}_{3}}{{m}_{3}}=\frac{30}{18}=1.66 \mathrm{m}/{\mathrm{s}}^{2}
Aceleración del cuarto cuerpo.
{a}_{4}=\frac{{F}_{4}}{{m}_{4}}=\frac{25}{40}=0.625 \mathrm{m}/{\mathrm{s}}^{2}
Ordenando de forma ascendente: 4, 2, 3, 1.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 6
La torca neta aplicada a un objeto rígido tiende a producir:
- inercia rotacional
- aceleración lineal
- equilibrio rotacional
- aceleración angular
Solución:
En la dinámica rotacional, la torca o torque es el análogo a la fuerza en la dinámica traslacional. Teniendo en cuenta esto, la inercia rotacional es el análogo a la masa y la aceleración angular es análoga a la aceleración lineal.
\tau =I\cdot \alpha
Concluimos el problema indicando al inciso d) como la respuesta correcta.
Reactivo 7
En un recipiente de 8 m de ancho, 10 m de largo y 3.5 m de profundidad, se tiene almacenada agua pura con una densidad de 1\times {10}^{3}\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} . Determinar el volumen del agua considerando que el recipiente esté lleno al 75% de su capacidad.
- 40{\mathrm{m}}^{3}
- 60{\mathrm{m}}^{3}
- 210{\mathrm{m}}^{3}
- 280{\mathrm{m}}^{3}
Solución:
Para calcular el volumen que ocupa el agua, primero calculamos el volumen total del recipiente y luego calculamos el 75% del resultado, ya que la sustancia ocupa este mismo porcentaje del recipiente.
El volumen de un paralelepípedo se calcula como el producto de sus tres dimensiones.
V=8\times 10\times 3.5=280 {\mathrm{m}}^{3}
Calculamos el 75%:
{V}_{agua}=\left(280\right)\left(0.75\right)=210 {\mathrm{m}}^{3}
El agua ocupa 210 metros cúbicos de volumen en el recipiente.
La respuesta correcta es el inciso c).
Reactivo 8
Si a un resorte se le cuelga una masa de 3.0 kg y se produce en el primero una deformación de 0.2 m, ¿cuál será el valor de su constante?
- 147.15 N/m
- 250.6 N/m
- 300.0 N/m
- 1306.0 N/m
Solución:
El módulo de la fuerza debido a la deformación producida sobre un resorte, se calcula mediante la Ley de Hooke.
F=k\mathrm{\Delta }x
Esta ecuación tiene un signo menos en su forma vectorial, porque la fuerza elástica se opone al sentido de la deformación.
Despejamos a la constante elástica k .
k=\frac{F}{\mathrm{\Delta }x}
La fuerza en este caso es producida por el peso del cuero: F=mg . Asumimos a la gravedad como 9.81 \mathrm{m}/{\mathrm{s}}^{2} .
k=\frac{mg}{\mathrm{\Delta }x}=\frac{\left(3\right)\left(9.81\right)}{0.2}=147.15\frac{\mathrm{N}}{\mathrm{m}}
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 9
Se cuelga de un muelle una bola de 20 kg de masa cuya constante elástica vale 2200 N/m. Determinar el alargamiento del muelle en centímetros.
- 8.9 cm
- 70 cm
- 700.9 cm
- 714 cm
Solución:
En este caso debemos aplicar la Ley de Hooke para el cálculo del alargamiento del muelle. La fuerza que actúa sobre el resorte es debido al peso de la bola, es decir: F=mg . Sustituimos en la Ley de Hooke y despejamos la deformación:
F=k\mathrm{\Delta }x\to \mathrm{\Delta }x=\frac{mg}{k}
\mathrm{\Delta }x=\frac{\left(20\right)\left(9.81\right)}{2200}=0.089 \mathrm{m}
Convertimos a centímetros dividiendo entre 100.
\mathrm{\Delta }x=8.9 \mathrm{c}\mathrm{m}
El muelle se deforma 8.9 centímetros debido al peso de la bola.
Seleccionamos como respuesta correcta al inciso a).
Reactivo 10
Considerar una masa m que cuelga de un resorte de constante k en equilibrio, en un lugar donde la gravedad es 9.81 m/s. ¿Qué proporción debe tener la constante del resorte k y la masa m para que el resorte estire 30 cm?
- 0.327{\mathrm{s}}^{-2}
- 32.7{\mathrm{s}}^{-2}
- 327.1{\mathrm{s}}^{-2}
- 3277.7{\mathrm{s}}^{-2}
Solución:
Convertimos la deformación del resorte a metros.
\mathrm{\Delta }x=0.3 \mathrm{m}
Ahora, despejamos de la ecuación de la Ley de Hooke la razón entre la constante del resorte y la masa, teniendo en cuenta que la fuerza ejercida es debido al peso de la masa.
mg=k\mathrm{\Delta }x\to \frac{k}{m}=\frac{g}{\mathrm{\Delta }x}
Sustituimos los valores en la igualdad:
\frac{k}{m}=\frac{9.81 \mathrm{m}/{\mathrm{s}}^{2}}{0.3 \mathrm{m}}=32.7\frac{1}{{\mathrm{s}}^{2}}=32.7 {\mathrm{s}}^{-2}
La relación entre la constante elástica y la masa debe ser de 32.7 {\mathrm{s}}^{-2} .
La respuesta correcta es el inciso b).