En este artículo, nos sumergiremos en la resolución de los reactivos del 21 al 30 del módulo de Cálculo del EXANI II. Estos ejercicios te ayudarán a practicar conceptos avanzados de cálculo, como límites, derivadas y optimización, fundamentales para afrontar con éxito el examen.

Cada problema te presenta un escenario diferente que pondrá a prueba tu capacidad para aplicar las reglas y teoremas del cálculo. Desde la regla de L’Hôpital hasta el Teorema del Valor Medio, estos reactivos te brindarán una experiencia completa de lo que puedes esperar en la prueba real.
Temas que cubrimos en estos reactivos:
- Aplicación de la regla de L’Hôpital
- Cálculo de extremos absolutos de funciones
- Intervalos de concavidad y convexidad
- Optimización de áreas
- Teorema del Valor Medio
- Diferenciales y sus aplicaciones
- Variaciones de funciones y población
- Integrales indefinidas y primitivas
- Relación de integrales inmediatas
Estos ejercicios te permitirán afianzar tus conocimientos en cálculo y ganar confianza para enfrentarte a los problemas más desafiantes del examen. ¡Comencemos!
Reactivo 21
Resuelva el siguiente límite aplicando la regla de L´ Hopital.
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)
- L=1
- L=-1
- L=-2
Solución:
La regla de L’ Hopital nos dice que podemos resolver cualquier límite de una función racional con solo derivar el numerador y denominador a la vez. Primero debemos expresar a la función como un cociente, empleando el siguiente truco algebraico:
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)=\underset{x\to \infty }{\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{x-1}{x+1}\right)}{\frac{1}{x}}
Aplicando la regla de L’ Hopital:
\underset{x\to \infty }{\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{x-1}{x+1}\right)}{\frac{1}{x}}=\underset{x\to \infty }{\mathrm{lim}}\frac{{\left[\mathrm{ln}\left(\frac{x-1}{x+1}\right)\right]}^{\text{'}}}{{\left[\frac{1}{x}\right]}^{\text{'}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{\frac{x-1}{x+1}}}{-\frac{1}{{x}^{2}}}
Simplificamos antes de continuar derivando.
\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{\frac{x-1}{x+1}}}{-\frac{1}{{x}^{2}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{\left(x+1\right){\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{x-1}}{-\frac{1}{{x}^{2}}}=-\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}\left(x+1\right){\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{x-1}
Para evitar complicar la expresión, resolveremos la derivada indicada aparte.
{\left(\frac{x-1}{x+1}\right)}^{\text{'}}=\frac{{\left(x-1\right)}^{\text{'}}\left(x+1\right)-{\left(x+1\right)}^{\text{'}}\left(x-1\right)}{{\left(x+1\right)}^{2}}=\frac{x+1-x+1}{{\left(x+1\right)}^{2}}=\frac{2}{{\left(x+1\right)}^{2}}
Sustituimos en el límite.
-\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}\left(x+1\right)\frac{2}{{\left(x+1\right)}^{2}}}{x-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{x}^{2}}{\left(x+1\right)}}{x-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{\left(x-1\right)\left(x+1\right)}
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{\left(x-1\right)\left(x+1\right)}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}
Evaluamos:
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}=\frac{\infty }{\infty }
Aplicamos de nuevo la regla de L’Hopital.
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{2x}{2x}=-2\underset{x\to \infty }{\mathrm{lim}}1
Evaluando:
-2\underset{x\to \infty }{\mathrm{lim}}1=-2
Finalmente:
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)=-2
La respuesta correcta es el inciso c).
Reactivo 22
Calcule los valores de x para los extremos absolutos de la función real indicada a continuación en el intervalo \left[-2, 2\right] .
f\left(x\right)=\frac{x+2}{{e}^{x}}
- x=-1
- x=e
- x=\frac{1}{e}
Solución:
Los extremos de una función corresponden a los mínimos y máximos en un intervalo dado. Podemos calcular dichos puntos igualando a cero la derivada de la función. Nos quedaremos con aquellos extremos que se encuentren dentro del intervalo dado.
Derivada de la función.
{f}^{\text{'}}\left(x\right)={\left(\frac{x+2}{{e}^{x}}\right)}^{\text{'}}=\frac{{{e}^{x}\left(x+2\right)}^{\text{'}}-{\left({e}^{x}\right)}^{\text{'}}\left(x+2\right)}{{e}^{2x}}
{f}^{\text{'}}\left(x\right)=\frac{{e}^{x}-{e}^{x}\left(x+2\right)}{{e}^{2x}}=\frac{1-\left(x+2\right)}{{e}^{x}}=-\frac{x+1}{{e}^{x}}
{f}^{\text{'}}\left(x\right)=-\frac{x+1}{{e}^{x}}
Igualamos a cero la derivada.
-\frac{x+1}{{e}^{x}}=0
La fracción será cero sólo cuando el denominador se anule.
x+1=0\to x=-1
El extremo se encuentra dentro del intervalo.
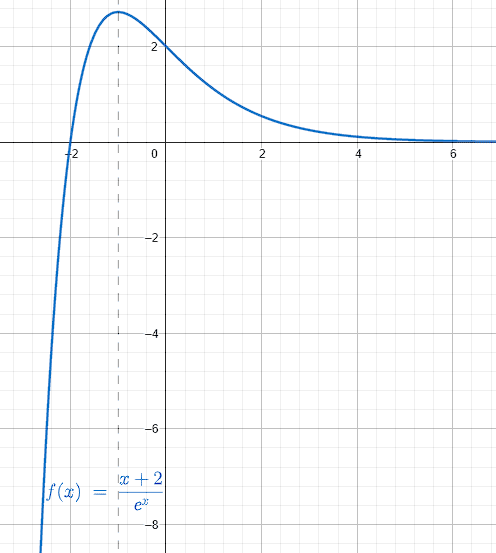
La respuesta correcta es el inciso a).
Reactivo 23
Dada la función f\left(x\right)=2{x}^{3}+3{x}^{2}-12x+6 , calcule los intervalos de concavidad.
- \left(-\infty , -\frac{1}{2}\right)
- \left(-\infty , -1\right) y \left(1, \infty \right)
- \left(-\frac{1}{2}, \frac{1}{2}\right)
Solución:
Una función es cóncava en un punto si su segunda derivada es negativa. El intervalo de concavidad o convexidad, se obtiene mediante los puntos de inflexión de la función: puntos en los que la pendiente de la recta tangente cambia de signo.
El procedimiento a seguir es: calculamos la segunda derivada de la función, obtenemos los puntos de inflexión y evaluamos entre cuáles valores es negativa.
Segunda derivada de la función:
{f}^{\text{'}}\left(x\right)=6{x}^{2}+6x-12
{f}^{\text{'}\text{'}}\left(x\right)=12x+6
Igualamos a cero para encontrar el punto de inflexión.
12x+6=0\to x=-\frac{1}{2}
Sustituimos un valor de x antes y después de -\frac{1}{2} para comprobar en qué intervalo es negativa la segunda derivada.
Evaluando un punto antes.
{x}^{-}=-1\to {f}^{\text{'}\text{'}}\left(x=-1\right)=12\left(-1\right)+6=-6
La función es cóncava en el intervalo entre -\infty y -\frac{1}{2} sin incluir.
\left(-\infty , -\frac{1}{2}\right)
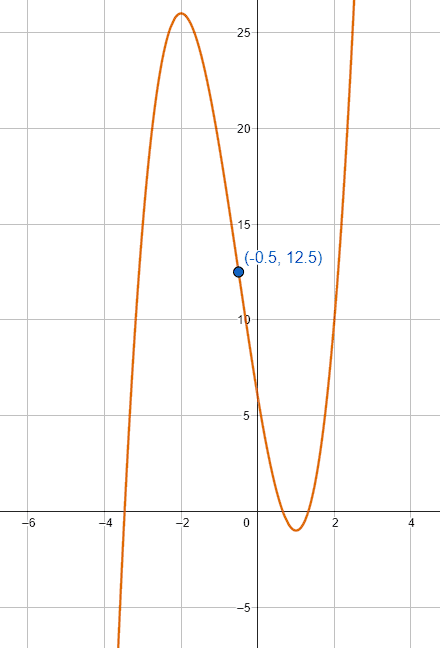
La respuesta correcta es el inciso a).
Reactivo 24
A partir de un tronco de sección perfectamente circular con radio igual a 3 m, se desea obtener una viga rectangular. ¿Cuáles deberían ser las dimensiones de la viga sobre la sección circular para que dicha viga tenga área máxima?
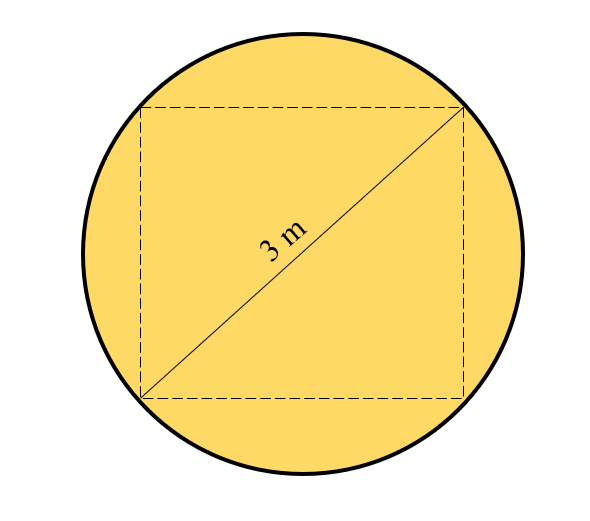
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=3,\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=2
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\frac{3\sqrt{2}}{2},\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=\frac{3\sqrt{2}}{2}
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\sqrt{2},\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=2
Solución:
El área de la viga rectangular se calcula como base b por altura a .
A=b\cdot a
Por otra parte, la diagonal del rectángulo debe ser igual al radio del tronco. Aplicando el teorema de Pitágoras:
{3}^{2}={a}^{2}+{b}^{2}
Despejamos una de las variables de la ecuación de la diagonal.
b=\sqrt{9-{a}^{2}}
Sustituimos en la función del área:
A=a\sqrt{9-{a}^{2}}
Con esta función, encontramos el máximo valor de altura derivando e igualando a cero.
\frac{dA}{da}={\left(a\sqrt{9-{a}^{2}}\right)}^{\text{'}}={\left(a\right)}^{\text{'}}\sqrt{9-{a}^{2}}+{\left(\sqrt{9-{a}^{2}}\right)}^{\text{'}}a
Resolvemos:
\sqrt{9-{a}^{2}}+\frac{1}{2}{\left(9-{a}^{2}\right)}^{\text{'}}{\left(9-{a}^{2}\right)}^{-\frac{1}{2}}=\sqrt{9-{a}^{2}}+\frac{1}{2}\left(-2a\right){\left(9-{a}^{2}\right)}^{-\frac{1}{2}}
\frac{dA}{da}=\sqrt{9-{a}^{2}}-\frac{a}{\sqrt{9-{a}^{2}}}=\frac{-2{a}^{2}+9}{\sqrt{9-{a}^{2}}}
Igualamos a cero.
\frac{-2{a}^{2}+9}{\sqrt{9-{a}^{2}}}=0\to -2{a}^{2}+9=0
Resolviendo nos queda:
{a}_{1}=\frac{3}{\sqrt{2}}, {a}_{2}=-\frac{3}{\sqrt{2}}
Nos quedamos con el resultado positivo.
a=\frac{3}{\sqrt{2}}
Sustituimos en la ecuación de la diagonal para despejar a b .
b=\sqrt{9-{\left(\frac{3}{\sqrt{2}}\right)}^{2}}=\sqrt{9-\frac{9}{2}}=\sqrt{\frac{18-9}{2}}=\frac{3}{\sqrt{2}}
Finalmente:
\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\frac{3\sqrt{2}}{2}, \mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=\frac{3\sqrt{2}}{2}
La respuesta correcta es el inciso b).
Reactivo 25
Calcular los valores de x en el intervalo \left[-1, 1\right] que satisfacen el teorema del valor medio para la función g\left(x\right)=-2{x}^{3}+{x}^{2}+x+1 .
Recuerde que:
{f}^{\text{'}}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}
- {c}_{1}=\frac{1}{6}, {c}_{2}=-\frac{1}{6}
- {c}_{1}=\frac{\sqrt{13}}{6}, {c}_{2}=-\frac{\sqrt{13}}{6}
- {c}_{1}=\frac{1-\sqrt{13}}{6}, {c}_{2}=\frac{1+\sqrt{13}}{6}
Solución:
En este caso, debemos obtener el valor de c a partir de la ecuación que se muestra en el enunciado. Encontramos a f\left(a\right) y f\left(b\right) sustituyendo los extremos del intervalo en la función.
a=-1\to f\left(-1\right)=3
b=1\to f\left(1\right)=1
Ahora, calculamos la derivada de f .
{f}^{\text{'}}\left(x\right)=-6{x}^{2}+2x+1\to {f}^{\text{'}}\left(c\right)=-6{c}^{2}+2c+1
Sustituimos todo en la ecuación del valor medio.
-6{c}^{2}+2c+1=\frac{1-3}{1+1}=-1
-6{c}^{2}+2c+2=0\to 3{c}^{2}-c-1=0
Aplicando la fórmula de la resolvente:
{c}_{1}=\frac{1-\sqrt{13}}{6}, {c}_{2}=\frac{1+\sqrt{13}}{6}
Indicamos como respuesta correcta al inciso c).
Reactivo 26
Dada la función f\left(x\right)={x}^{3}-2{x}^{2}+x+3 , calcule su diferencial.
- df=\left(3{x}^{2}-4x+1\right)dx
- df=dx
- df=\left({x}^{3}-2{x}^{2}+x\right)dx
Solución:
El diferencial de una función se encuentra aplicando la derivada de la siguiente forma:
\frac{df}{dx}={f}^{\text{'}}\left(x\right)\to df={f}^{\text{'}}\left(x\right)dx
Calculamos la derivada de la función en el diferencial:
df={\left({x}^{3}-2{x}^{2}+x+3\right)}^{\text{'}}dx
df=\left(3{x}^{2}-4x+1\right)dx
La respuesta correcta es la opción a).
Reactivo 27
La función de crecimiento de una población de bacterias viene dada por la siguiente expresión:
g\left(x\right)=\sqrt{x+1}
Si un grupo de investigadores ha encontrado una variación \mathrm{\Delta }x=0.5 cuando x=1 , ¿cuánto vale la variación de la población?
- dg\left(x\right)=\frac{8}{\sqrt{2}}
- dg\left(x\right)=\frac{\sqrt{2}}{8}
- dg\left(x\right)=0
Solución:
En términos geométricos, el diferencial dg de una función g\left(x\right) representa la variación que esta experimenta ante una variación en la variable independiente. El diferencial se calcula como:
dg={g}^{\text{'}}\left(x\right)dx
Derivamos a la función:
{g}^{\text{'}}\left(x\right)={\left(\sqrt{x+1}\right)}^{\text{'}}=\frac{1}{2}{\left(x+1\right)}^{\text{'}}{\left(x+1\right)}^{\frac{1}{2}-1}=\frac{1}{2\sqrt{x+1}}
Sustituyendo en el diferencial:
dg=\frac{1}{2\sqrt{x+1}}dx
Evaluamos.
dg=\frac{1}{2\sqrt{1+1}}\left(0.5\right)=\frac{1}{4\sqrt{2}}=\frac{\sqrt{2}}{8}
Finalmente, la población tiene una variación de:
dg=\frac{\sqrt{2}}{8}\approx 0.17677
La respuesta correcta es el inciso b).
Reactivo 28
Sea el diferencial de una función como df\left(x\right)=\left(3{x}^{2}+1\right)dx , ¿cuál de las siguientes opciones representa una familia de curvas a la que pertenece la función original?
- f\left(x\right)={x}^{3}+x+C
- f\left(x\right)={x}^{3}+x
- f\left(x\right)=3{x}^{2}+1+C
Solución:
Para deshacer el operador diferencial, debemos integrar en ambos miembros de la ecuación.
df\left(x\right)=\left(3{x}^{2}+1\right)dx\to \int df\left(x\right)=\int \left(3{x}^{2}+1\right)dx
f\left(x\right)=\int \left(3{x}^{2}+1\right)dx
Separamos en dos integrales simples aplicando la propiedad de la suma.
f\left(x\right)=\int \left(3{x}^{2}+1\right)dx=3\int {x}^{2}dx+3\int dx
Empleamos la fórmula de la integral de una potencia y del diferencial.
f\left(x\right)=\frac{3{x}^{2+1}}{2+1}+3x+C
La familia de curvas a la que pertenece la función original es:
f\left(x\right)={x}^{3}+3x+C
Indicamos como respuesta correcta al inciso a).
Reactivo 29
Calcula la siguiente integral indefinida.
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx
- I=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
- I=\frac{{x}^{2}}{2}-\frac{4}{x}+C
- I=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}
Solución:
Iniciamos la solución de la integral separando en fracciones simples.
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx=\int \frac{{x}^{3}}{{x}^{2}}dx-\int \frac{x}{{x}^{2}}dx+\int \frac{4}{{x}^{2}}dx
Simplificamos:
\int \frac{{x}^{3}}{{x}^{2}}dx-\int \frac{x}{{x}^{2}}dx+\int \frac{4}{{x}^{2}}dx=\int xdx-\int \frac{1}{x}dx+4\int \frac{1}{{x}^{2}}dx
Ahora, integramos aplicando las fórmulas inmediatas correspondientes.
\int xdx-\int \frac{1}{x}dx+4\int {x}^{-2}dx=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
Finalmente:
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
La respuesta correcta es el inciso a).
Reactivo 30
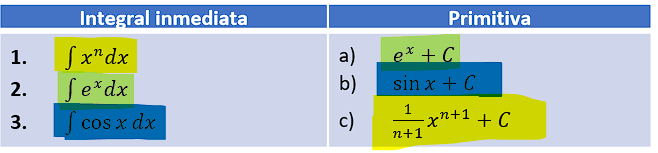
Relacione cada integral inmediata con su primitiva.
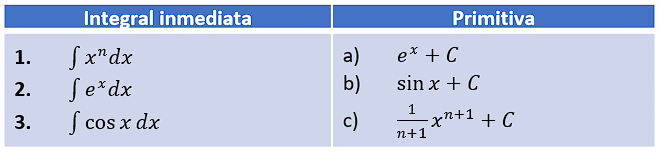
- 1a, 2c, 3b
- 1c, 2b, 3a
- 1c, 2a, 3b
Solución:
Vamos a ir resolviendo cada una de las integrales en la columna izquierda para relacionarla con su respectiva primitiva en la columna derecha.
Primera integral.
\int {x}^{n}dx
Esta integral es la forma general de la integral de una potencia.
\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+C
1c.
Segunda integral.
\int {e}^{x}dx
Resolvemos aplicando la integral de una exponencial.
\int {e}^{x}dx={e}^{x}+C
2a.
Por descarte: 3b. Uniendo las respuestas parciales:
1c, 2a, 3b.
La respuesta correcta es el inciso c).

