El principio de Pascal, es una de las principales leyes de la hidrostática presente en numerosas aplicaciones mecánicas de nuestro día a día y constituye la columna vertebral para el resto de fenómenos que estudian la estática de fluidos.

En este tutorial, vamos a estudiar a detalle cada aspecto del principio de Pascal, incluiremos ejemplos y ejercicios resueltos, los cuales recomiendo desarrolles por tu cuenta antes de mirar la respuesta.
Principio de pascal
Enunciada por el físico y matemático Blasie Pascal, es una ley que establece que la fuerza aplicada en la superficie de un fluido en reposo (es decir, la velocidad de sus partículas es cero) e incompresible se transmite con la misma intensidad en todas las direcciones de dicha sustancia; siempre que el recipiente en el que se encuentre no se deforme.
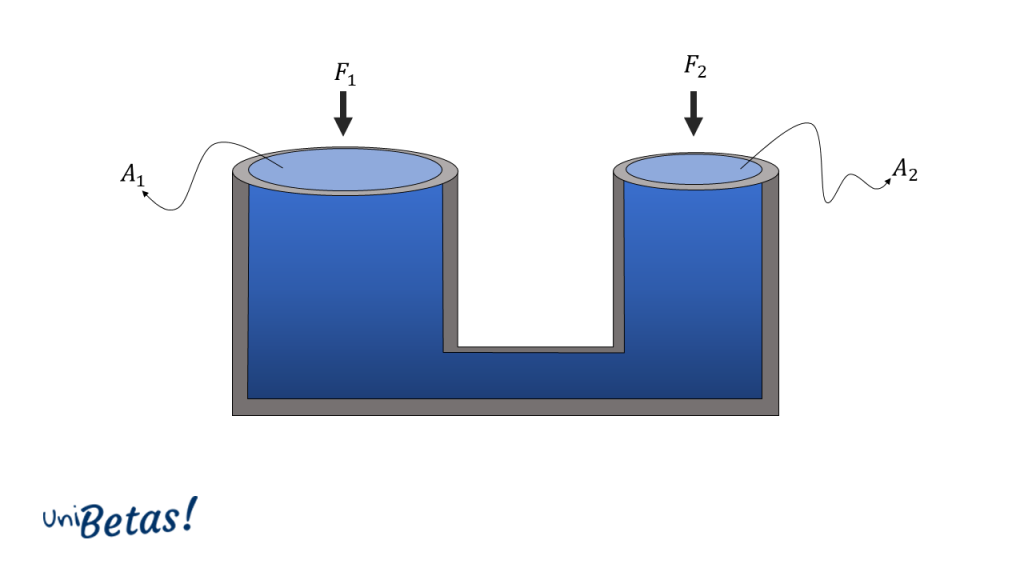
Dicho de otra forma, la presión ejercida sobre un fluido en alguna parte del mismo se esparcirá uniformemente por todo su volumen. Recordando que P=F/A (fuerza entre el área) podemos expresar a la presión dentro del fluido estático de dos formas:
P=\frac{{F}_{1}}{{A}_{1}}
P=\frac{{F}_{2}}{{A}_{2}}
Igualamos ambas ecuaciones:
\frac{{F}_{1}}{{A}_{1}}=\frac{{F}_{2}}{{A}_{2}}
Por tanto, si se aplica una fuerza {F}_{1} en la placa con superficie {A}_{1} , debido al principio de Pascal, en la placa con área {A}_{2} se siente una fuerza igual a:
{F}_{2}={F}_{1}\frac{{A}_{2}}{{A}_{1}}
Es decir, que si el área {A}_{2}>{A}_{1} , la fuerza que se siente {F}_{2} es mayor que la fuerza aplicada {F}_{1} . Este es el principio de las prensas hidráulicas, con un buen ajuste de las áreas, aplicando una pequeña fuerza podemos levantar un coche.
¿Qué es un fluido?
En la definición del principio de Pascal, se mencionó un par de condiciones que deben cumplirse: que el fluido sea incompresible y que se encuentre en reposo.
Existen diferentes maneras de clasificar a los fluidos, pero la que nos interesa en este caso es respecto a su compresibilidad. Un fluido es compresible si su volumen cambia cuando varía la presión, por el contrario, los incompresibles son aquellos cuyo volumen no cambia al variar la presión.
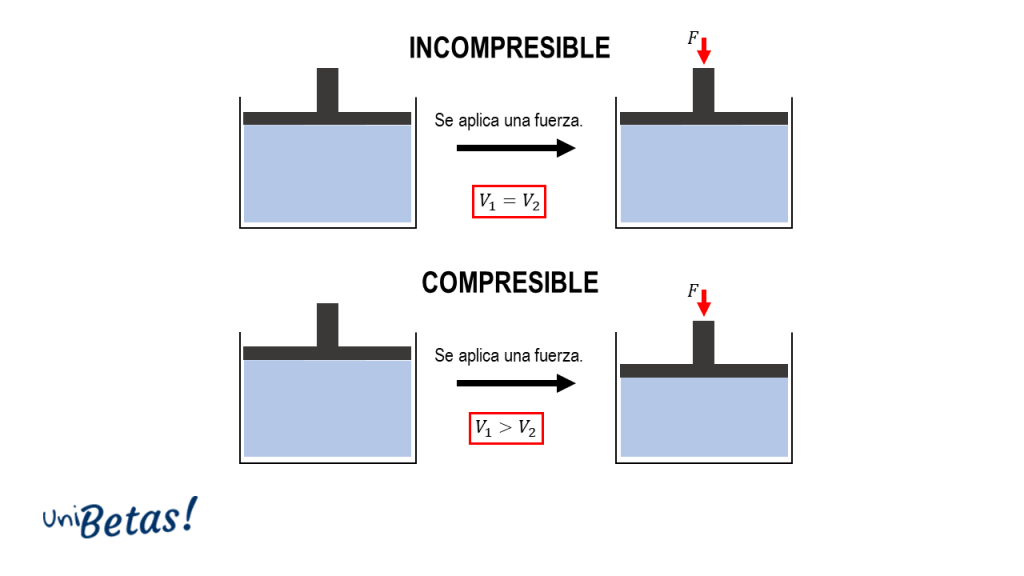
Estos últimos son los que se estudian mediante el principio de Pascal.
Ejemplo Principio de Pascal: la prensa hidráulica
Una prensa hidráulica es un sistema formado por dos cilindros verticales comunicados, de tal forma que el área de la sección transversal de uno es menor que la del otro. Así, se logra elevar grandes masas en el área mayor cuando se aplica una pequeña fuerza sobre la sección transversal menor.
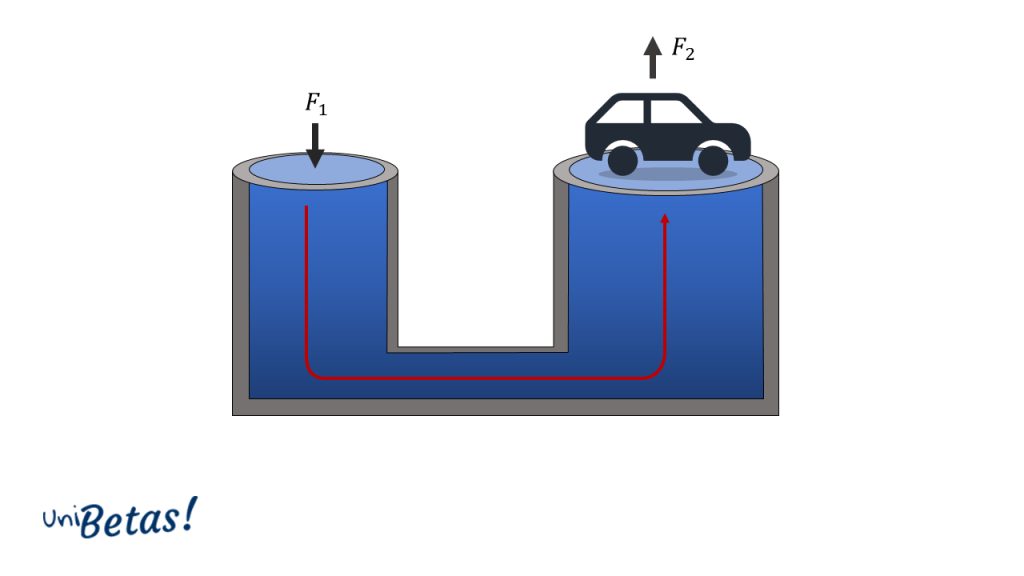
Principio de Pascal ejercicios
Reactivo 1
El dueño de un taller desea adquirir una prensa hidráulica de banco para plegar láminas de aluminio. En base a su experiencia, sabe que las láminas se doblan cuando se aplica una presión de 10 \mathrm{N}/{\mathrm{m}}^{2} ¿Cuál debe ser la fuerza aplicada por un operario si el área de la fuerza {F}_{1} es igual a 1{\mathrm{m}}^{2} ?
Solución:
Sabemos que el principio de Pascal establece que la presión ejercida en una parte de un fluido se transmite uniformemente por el mismo, de esta forma, si queremos aplicar 10 \mathrm{N}/{\mathrm{m}}^{2} sobre la lámina para plegar, el operario debe aplicar una presión igual en el área {A}_{1}=1 {\mathrm{m}}^{2} .
P=\frac{{F}_{1}}{{A}_{1}}\to {F}_{1}=P\bullet {A}_{1}
Sustituyendo.
{F}_{1}=\left(10 \mathrm{N}/{\mathrm{m}}^{2}\right)\left(1 {\mathrm{m}}^{2}\right)=10 \mathrm{N}
El operario debe aplicar 10 Newtons de fuerza para plegar la lámina.
Reactivo 2
Dado el sistema de la figura.
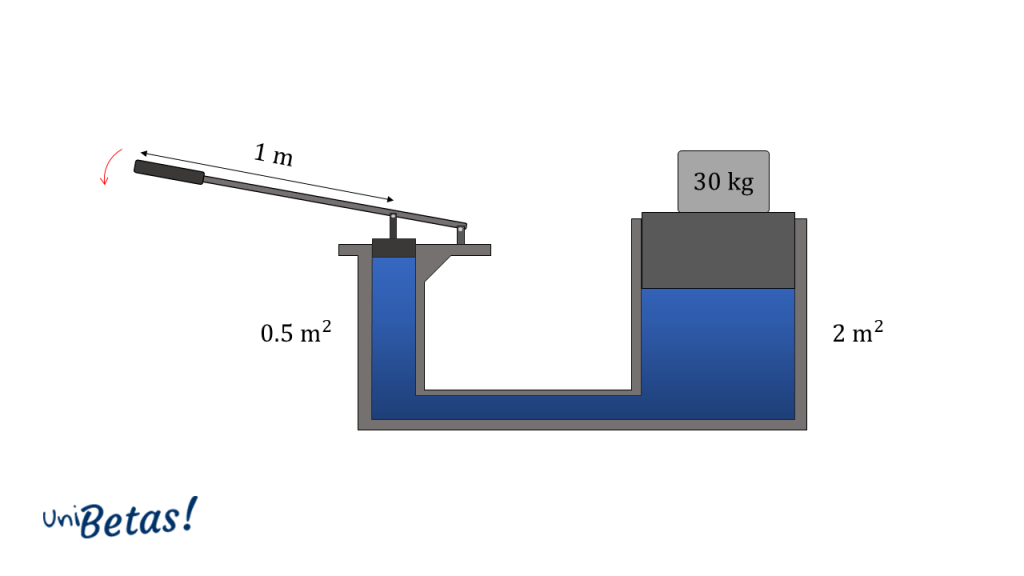
Calcule la magnitud del torque que se debe aplicar para desplazar la masa.
Solución:
Debemos aplicar el principio de Pascal para resolver este problema:
\frac{{F}_{2}}{{A}_{2}}=\frac{{F}_{1}}{{A}_{1}}
Debido a que nos interesa la fuerza aplicada en el área 1 para luego relacionarla con el torque, es a esta a la que vamos a despejar.
{F}_{1}=\frac{{A}_{1}}{{A}_{2}}{F}_{2}
Ahora, la fuerza 2 es igual al peso de la masa, es decir {F}_{2}=mg .
{F}_{1}=\frac{{A}_{1}}{{A}_{2}}mg
Además, de la mecánica clásica sabemos que la magnitud del torque es \tau =Fr . Donde r es el radio de la barra. Sustituyendo nos queda:
{F}_{1}=\frac{\tau }{r}\to \tau =\frac{{A}_{1}}{{A}_{2}}mgr
Evaluamos la expresión.
\tau =\frac{0.5}{2}\left(30 \mathrm{k}\mathrm{g}\right)\left(9.8\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right)\left(1 \mathrm{m}\right)=73.5 \mathrm{N}\mathrm{m}
Se deben aplicar 73.5 Newtons por metro de torque.