Mini simulacro UABC de Matemáticas | Reactivos resueltos

Vamos a resolver los 4 ejercicios de matemáticas del mini simulacro de examen, basados en la nueva guía de estudios ExIES de la UABC.

El examen de ingreso a la UABC ha cambiado. Ya no es Exani II, el nuevo formato de examen se llama ExIES y está basado en competencias.  Si quieres conocer el temario completo de matemáticas, visita el post de la guía UABC 2023.

¿Cómo es el nuevo examen?

Consta de 160 reactivos, de los cuales 38 son preguntas piloto que no cuentan en el puntaje final. La siguiente tabla resume la estructura completa publicada en la convocatoria UABC 2023:

ÁREAS	PREGUNTAS
Lectura	36
Lengua Escrita	36
Matemáticas	50
Preguntas evaluativas	122
Preguntas piloto	38
TOTAL	160

Si eliminamos las preguntas de prueba, quedarían 50 reactivos de matemáticas, 36 reactivos de lectura y 36 de lengua escrita. Además de su estructura, el examen también ha cambiado de enfoque.

Tiene los mismos módulos que el Exani II, pero el examen se basa en competencias.

¿Cómo son los reactivos de examen? Los problemas son de selección múltiple, deberás escoger la respuesta correcta entre 4 opciones.

Temario de matemáticas

El temario no indica puntualmente los temas a estudiar, sino que establece una estructura por competencias para las preguntas del examen.

El temario que se muestra a continuación aplica para todas las carreras de la UABC.

Contenido	Reactivos
Herramientas Algebraicas: Resolución de problemas mediante el empleo de ecuaciones y sistemas lineales, ya sea a través de la representación de cantidades o de la representación gráfica	10
Problemas, Probabilidad y Análisis de Datos: Creación y análisis de relaciones, representación y análisis de datos cuantitativos y aplicación de probabilidades	15
Matemáticas Avanzadas: Creación de expresiones algebraicas y uso de gráficos que representan funciones exponenciales no lineales o cuadráticas	15
Temas Adicionales en Matemáticas: Solución de problemas asociados al área y volumen, aplicación de definiciones, teoremas sobre líneas, ángulos, triángulos y círculos	10
Total	50

1. Herramientas algebraicas.
   1. Planteamiento de una ecuación lineal con una variable mediante un contexto.
   2. Interpretación y solución de inecuaciones lineales con una variable.
   3. Construcción de una función lineal que represente la relación lineal entre dos variables.
   4. Interpretación y resolución de un sistema de ecuaciones lineales con tres variables.
   5. Interpretación y resolución de un sistema de ecuaciones lineales con dos variables.
   6. Resolución de ecuaciones lineales en una variable.
   7. Resolución de sistemas de ecuaciones lineales con dos variables.
   8. Interpretación de las características de una función lineal dentro de un contexto.
   9. Relación entre la representación gráfica y algebraica de una función lineal.
2. Problemas, probabilidad y análisis de datos.
   1. Resolución de problemas utilizando índices, tasas, relaciones proporcionales y dibujos a escalas mediante uno o varios pasos.
   2. Resolución de problemas utilizando porcentajes con uno o varios pasos.
   3. Resolución de problemas utilizando diferentes magnitudes, y diferentes sistemas de unidades.
   4. Análisis de variables involucradas en los diferentes modelos lineales, cuadráticos y exponenciales.
   5. Identificación de las características claves de un gráfico utilizando la relación entre las dos variables.
   6. Calcular frecuencias relativas y probabilidades (sumativa y multiplicativa).
   7. Realizar inferencias a partir de los datos de una muestra.
   8. Obtención de las medidas de tendencia central de datos y medidas de dispersión.
   9. Analizar reportes para hacer inferencias a partir de una tabla estadística.
3. Matemáticas avanzadas.
   1. Resolver problemas mediante funciones cuadráticas y exponenciales.
   2. Traducir contextos de lenguaje escrito a lenguaje algebraico.
   3. Convertir expresiones algebraicas con exponentes racionales a radicales y viceversa.
   4. Convertir ecuaciones de la forma ordinaria a la forma general y viceversa.
   5. Resolver ecuaciones cuadráticas.
   6. Simplificar operaciones aritméticas con polinomios.
   7. Resolver ecuaciones radicales y racionales en una variable.
   8. Resolución de un sistema de ecuaciones lineal y cuadrática.
   9. Simplificación de expresiones algebraicas (fracciones) complejas.
   10. Interpretación de parámetros, constantes o variables de una expresión no lineal en términos de un contexto dado.
   11. Comprensión y determinación de ceros y factores de polinomios para la elaboración de gráficos.
   12. Análisis de variables de expresiones algebraicas y su relación directa con el sistema de representación gráfico (sistemas de ecuaciones, descripción verbal del comportamiento gráfico, determinación de puntos importantes de una gráfica).
   13. Uso de notación de funciones e interpretación del significado de dichas notaciones (evaluación de funciones).
   14. Comprensión de las formas general, estándar o canónica de expresiones algebraicas para identificar parámetros de interés (vértice, ordenada en el origen).
4. Temas adicionales en matemáticas.
   1. Resolución de problemas que incluyan el cálculo de áreas o volúmenes de figuras geométricas.
   2. Uso de proporción trigonométrica y el Teorema de Pitágoras para resolver distintos problemas que consideran triángulos rectángulos.
   3. Resolución de triángulos oblicuángulos mediante ley de senos y ley de cosenos.
   4. Conversión entre grados y radianes y uso de radianes para determinar la longitud del arco; usar funciones trigonométricas en escala de radianes.
   5. Aplicación de teoremas sobre círculos para encontrar la longitud del arco, medidas de ángulos, longitud de la cuerda y áreas de un sector.
   6. Uso de conceptos y teoremas sobre congruencia y similitud para resolver problemas sobre líneas, ángulos y triángulos.
   7. Uso de la relación entre similitud, triángulo-rectángulo y proporciones trigonométricas; usar la relación entre seno y coseno de ángulos complementarios.
   8. Elaboración o uso de una ecuación en dos variables para resolver problemas sobre un círculo en un plano cartesiano.

¿Qué es una pregunta con competencias en matemáticas? Los reactivos plantean problemas reales que debes resolver aplicando las herramientas matemáticas previamente estudiadas en aritmética, álgebra o probabilidad.

Solución del simulacro de matemáticas

Mide el tiempo mientras desarrollas los reactivos, apunta los problemas que hayan sido desafiantes y activa el modo avión en tu teléfono durante el simulacro.  Recuerda que debes resolverlos por tu cuenta, utiliza este material como consulta.

Reactivo 7

Una persona compra una galleta y un café en una tienda, el café le cuesta el doble de la galleta menos 5 pesos, al llegar a la caja paga 25 pesos ¿Cuánto cuesta la galleta?

1. 9
2. 10
3. 13
4. 15

Solución:

Para encontrar el precio de la galleta, primero debemos transformar las relaciones entre los precios de los productos a expresiones algebraicas. Si el usuario pagó por el café y la galleta 25 pesos:

G+C=25

Además: … el café cuesta el doble de la galleta menos 5 pesos.

C=2G-5

Reemplazamos el precio del café en la primera ecuación.

G+C=25\to G+2G-5=25

Resolvemos.

3G=30\to G=10

La galleta cuesta 10 pesos.

Indicamos como respuesta correcta al inciso B.

Reactivo 8

A un grupo de estudiantes se les pregunta acerca de su música favorita obteniéndose la siguiente información.

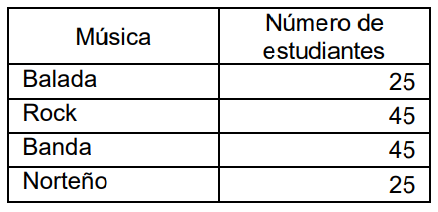
¿Cuál es la probabilidad de que al escoger al azar un estudiante de este grupo encuestado, le guste el rock o la balada?

1. P\left(A\right)=\frac{1}{2}
2. P\left(A\right)=\frac{5}{25}
3. P\left(A\right)=\frac{6}{25}
4. P\left(A\right)=\frac{14}{25}

Solución:

En este caso, el cálculo de la probabilidad se realizar mediante la fórmula de Laplace:

P\left(A\right)=\frac{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{f}\mathrm{a}\mathrm{v}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{s}}{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{ }\mathrm{m}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}}

El conector lógico “o” entre el número de estudiantes que les gusta el rock y a quienes les gusta la balada, nos dice que debemos sumar ambas cantidades para obtener el total de casos favorables.

P\left(A\right)=\frac{25+45}{25+45+45+25}=\frac{70}{140}=\frac{1}{2}

La probabilidad de escoger a un estudiante que le guste el rock o la balada es del 50%.

La respuesta correcta es el inciso A.

Reactivo 9

Una empresa de desechos tóxicos utiliza barriles con un diámetro de 6 pies y una altura igual al doble del diámetro. ¿Cuál es la capacidad () del barril?

1. V=36\pi
2. V=48\pi
3. V=72\pi
4. V=108\pi

Solución:

La fórmula para calcular el volumen de un cilindro es:

V=\frac{\pi {D}^{2}h}{4}

Donde D es el diámetro del cilindro y h es la altura. El enunciado nos dice que la altura es el doble del diámetro.

h=2\left(6\right)=12 \mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}

Sustituimos.

V=\frac{\pi {\left(6\right)}^{2}\left(12\right)}{4}=108\pi  {\mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}}^{3}

El barril tiene una capacidad de 108\pi  {\mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}}^{3} .

La respuesta correcta es el inciso D.

Reactivo 10

Un avión en su despegue sigue una trayectoria en línea recta representada por la ecuación:

y=\frac{1}{5}x

La torre de control observa que pasa un objeto no identificado perpendicularmente a la trayectoria del avión en el punto (10,2). ¿Cuál es la ecuación que describe la trayectoria del objeto no identificado?

1. -5x+y+52=0
2. x-5y+52=0
3. x+5y-52=0
4. 5x+y-52=0

Solución:

Debemos encontrar la recta perpendicular a y=\frac{1}{5}x y que pasa por el punto \left(10, 2\right) . La pendiente de la recta perpendicular se calcula mediante la siguiente relación:

{m}_{2}=-\frac{1}{{m}_{1}}

La pendiente {m}_{1}=\frac{1}{5} , sustituimos:

{m}_{2}=-\frac{1}{\frac{1}{5}}=-5

Sustituimos la pendiente y el punto en la ecuación punto pendiente de la recta.

y-{y}_{o}=m\left(x-{x}_{o}\right)\to y-2=-5\left(x-10\right)

y=-5x+50+2=-5x+52

\therefore 5x+y-52=0

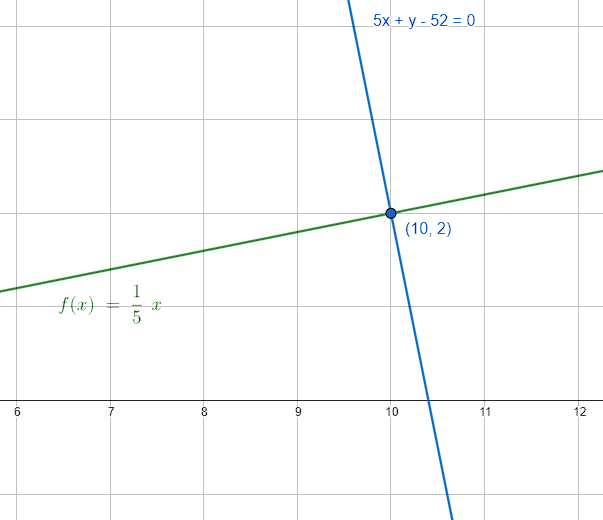
Concluimos indicando como respuesta correcta al inciso D.