Simulador examen IPN Física P.5: Ing. y C.s Físico Matemáticas

Llegamos a la quinta y última parte del simulacro de física para el área de Ingeniería y Ciencias Físico Matemáticas del Instituto Politécnico Nacional.

¡Felicidades por llegar hasta el final! Recuerda tomar descansos entre grupos de reactivos y parar durante un rato si algún problema se resiste a ser resuelto. Las mejores ideas surgen cuando permitimos que nuestro cerebro se oxigene de forma adecuada.

Reactivo 41

En un movimiento armónico simple descrito como x\left(t\right)=A\mathrm{sin}\left(\omega t+\theta \right) , ¿en qué posición ocurre la máxima velocidad?

1. Para x=A
2. Para x=0
3. Para x=\frac{A}{2}
4. Para x=-A

Solución:

Esta pregunta podemos responderla de dos formas: mediante un análisis cualitativo del MÁS o mediante las ecuaciones de posición, velocidad y aceleración. En este caso, lo haremos mediante las relaciones entre posición, velocidad y aceleración.

Comencemos por la descripción matemática del MAS:

x\left(t\right)=A\mathrm{sin}\left(\omega t+\theta \right)

Donde A es la amplitud, \theta  es el ángulo inicial y \omega  la velocidad angular. Si derivamos esta ecuación obtenemos la velocidad.

v\left(t\right)=\frac{dx\left(t\right)}{dt}

v\left(t\right)=\omega A\mathrm{cos}\left(\omega t+\theta \right)

La velocidad máxima ocurre cuando el coseno llega a su máximo valor, es decir:

\begin{array}{c}\omega t+\theta =0°\\ \omega t+\theta =180°\end{array}

Si sustituimos estos ángulos en la ecuación de posición obtenemos que:

{x}_{1}=A\mathrm{sin}\left(0\right)=0

{x}_{2}=A\mathrm{sin}\left(180°\right)=0

La máxima velocidad ocurre cuando el cuerpo pasa por el eje de oscilación, sea en ascenso o en descenso.

Este mismo resultado lo habríamos obtenido si el movimiento estuviese descrito mediante una función coseno, por tanto, este resultado aplica para cualquier MÁS. Concluimos que la respuesta es el inciso b).

Reactivo 42

En las celdas galvánicas, ¿qué función cumple el puente salino?

1. Aumentar el flujo de cargas
2. Permite balancear las reacciones de oxido reducción
3. Incrementa el potencial de oxidación
4. Permite el paso de los iones sin que las semiceldas se toquen directamente

Solución:

Las celdas galvánicas son dispositivos que aprovechan las reacciones de óxido reducción para producir un flujo de electrones y, con ello, generar energía eléctrica a partir de la reacción química espontánea.

Debido a que las reacciones de oxidación y reducción se dan en recipientes separados, es necesario mantener el flujo de electrones sin que las soluciones se toquen directamente, por ello, es necesario emplear un puente salino.

Este dispositivo, fabricado normalmente de Cloruro de Sodio o Potasio, mantiene el flujo de iones entre las semiceldas sin que entren en contacto directo. Concluimos comparando con las opciones que la respuesta correcta es la d).

Reactivo 43

Para un experimento de laboratorio, se planea utilizar Cobre y Cinc para elaborar una celda electroquímica. Si los potenciales normales de oxidación de cada elemento son {\epsilon }_{Cu}=-0.34\mathrm{ }\mathrm{V} y {\epsilon }_{\mathrm{Z}\mathrm{n}}=0.76\mathrm{ }\mathrm{V} , determine la especie que se oxida.

1. Se oxida el Cobre
2. Se oxida el Zinc
3. La reacción no es posible
4. Se oxidan ambos

Solución:

Las celdas electroquímicas están formadas por dos semiceldas una responsable de la oxidación y otra de la reducción, a esto se le conoce con el nombre de par electroquímico. Cada una de las especies tiene asociada una capacidad de donar electrones, la cual se cuantifica a partir del Potencial de Oxidación {\epsilon }_{o} .

Al momento de combinar dos pares para formar una celda, el de mayor potencial será el que proporcione electrones (se oxida) mientras que el otro recibe los electrones (se reduce).

Teniendo esto en cuenta, el potencial del Cinc según el enunciado, es mayor que el potencial del Cobre, por tanto, el Cinc será quien se oxide y el Cobre quien se reduzca.

{\mathrm{C}\mathrm{u}}^{+2}+{\mathrm{Z}\mathrm{n}}_{\left(\mathrm{s}\right)}\leftrightarrow {\mathrm{Z}\mathrm{n}}^{+2}+{\mathrm{C}\mathrm{u}}_{\left(\mathrm{s}\right)}

Reacción de la celda.

Concluimos indicando como respuesta correcta al inciso b).

Reactivo 44

A partir de la siguiente tabla de potenciales de oxidación, seleccione el par de especies que permiten obtener el máximo potencial en la celda galvánica.

1. Litio y oro
2. Hierro y plata
3. Níquel y Litio
4. Litio y plata

Solución:

Como sabemos, el voltaje de una celda electroquímica depende de los potenciales normales de oxidación de las especies que se emplean para construir las semiceldas. La diferencia de potencial entre los terminales de la celda se calcula como:

\mathrm{\Delta }\epsilon ={\epsilon }_{o}-{\epsilon }_{r}

Donde \mathrm{\Delta }\epsilon  es la diferencia de potencial, {\epsilon }_{o} es el potencial mayor y {\epsilon }_{r} es el menor potencial. Debido a que es una suma algebraica, la diferencia de potencial será mayor cuando {\epsilon }_{o} sea más positivo y {\epsilon }_{r} más negativo.

Examinando la tabla, el más positivo es \mathrm{L}\mathrm{i}/{\mathrm{L}\mathrm{i}}^{+} y el más negativo \mathrm{A}\mathrm{u}/{\mathrm{A}\mathrm{u}}^{+3} .

\mathrm{\Delta }\epsilon =3.045-\left(-1.498\right)=4.543 \mathrm{V}

Las especies que permiten el mayor potencial en la celda son el litio y el oro.

La respuesta correcta es el inciso a).

Reactivo 45

Determine la imagen que se forma al otro lado de la lente, a partir de la situación mostrada en la siguiente figura.

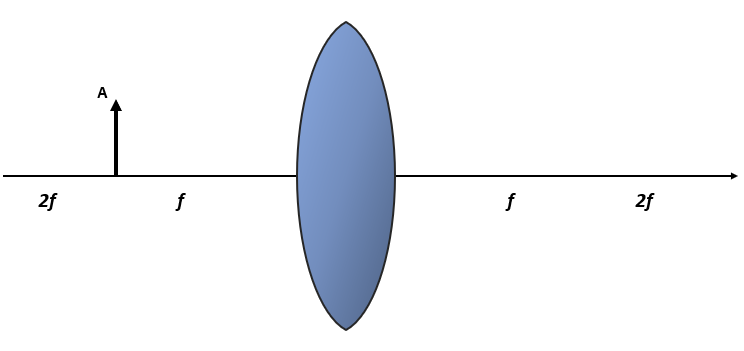
1. Real, invertida, de menor tamaño y situada entre f y 2f
2. Real, invertida, de mayor tamaño y situada más allá de 2f
3. No se forma imagen
4. Virtual, derecha y de mayor tamaño

Solución:

Recordemos que las lentes convergentes, son aquellas que concentran en un punto fijo llamado foco, los rayos que inciden paralelos al eje principal. Esta característica crucial, hace que la formación de imágenes con este tipo de lentes tenga que dividirse en 5 casos:

1. El objeto está entre 2f e infinito
2. El objeto está en 2f
3. El objeto está entre 2f y f
4. El objeto está en f
5. El objeto está a una distancia menor a f

En este caso, la posición del objeto concuerda con el caso 3 para el cual, la imagen que se forma del otro lado es: real, invertida, de mayor tamaño y situada más allá de 2f .

Comparando con los incisos, concluimos que la respuesta correcta es la opción b).

Reactivo 46

A partir de la figura que se muestra a continuación, seleccione el fenómeno físico que se observa.

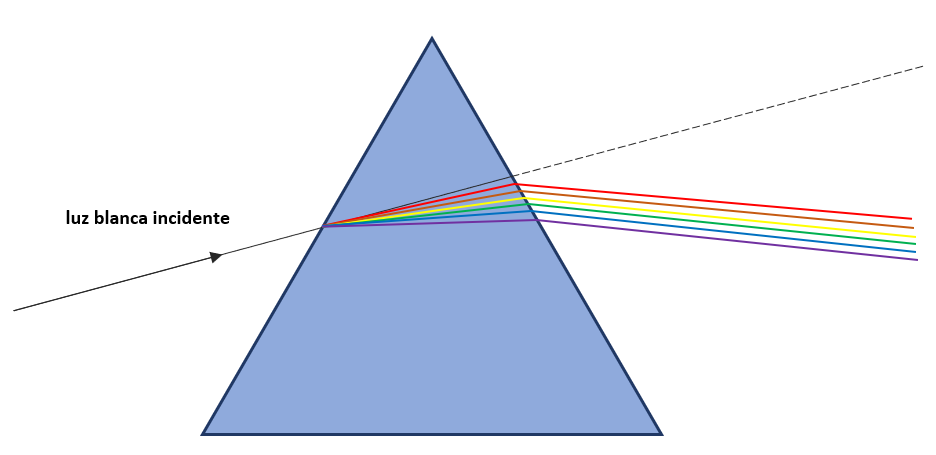
1. Refracción
2. Dispersión
3. Difracción
4. Reflexión

Solución:

En la figura vemos representado a un prisma, sobre el cual incide un rayo de luz blanca. Cuando la luz blanca incide sobre un prisma, la misma se descompone en el siguiente orden: rojo, anaranjado, amarillo, verde, azul y violeta.

Este fenómeno se debe a que el ángulo de refracción de la luz en cualquier medio varía según la longitud de onda.

La luz blanca es la suma de los colores anteriormente mencionados, cuando atraviesa un medio traslúcido cada color experimenta una desviación distinta de acuerdo a su longitud de onda.

Este fenómeno recibe el nombre de dispersión de la luz.

La respuesta correcta es el inciso b).

Reactivo 47

Suponga que dos bobinas se encuentran acopladas perfectamente a través de un núcleo ferromagnético, de tal forma que el flujo que circula por una también circula por la otra.

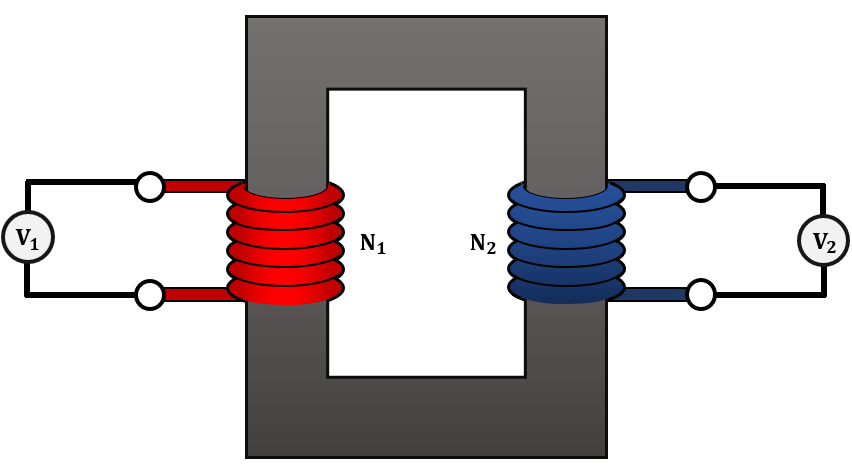
Demuestra la relación que existe entre las FEM y el número de espiras de las bobinas aplicando la ley de inducción de Faraday.

1. \frac{{V}_{1}}{{V}_{2}}=\frac{{n}_{2}}{{n}_{1}}
2. \frac{{V}_{1}}{{V}_{2}}=\frac{1}{{n}_{2}}
3. \frac{{V}_{1}}{{V}_{2}}={n}_{1}
4. \frac{{V}_{1}}{{V}_{2}}=\frac{{n}_{1}}{{n}_{2}}

Solución:

Comencemos por recordar lo que nos dice la ley de inducción de Faraday:

La fuerza electromotriz inducida en una bobina, es directamente proporcional al número de vueltas de la bobina y a la variación de flujo magnético a través de ella.

FEM=n\frac{d\mathrm{\Phi }}{dt}

Llevando esto a las bobinas del enunciado.

{V}_{1}={n}_{1}\frac{d{\mathrm{\Phi }}_{1}}{dt} y {V}_{2}={n}_{2}\frac{d{\mathrm{\Phi }}_{2}}{dt}

Debido a que las bobinas de la figura se encuentran perfectamente acopladas, el flujo magnético que pasa por una es igual al flujo que pasa por la otra {\mathrm{\Phi }}_{1}={\mathrm{\Phi }}_{2}=\mathrm{\Phi } . Las ecuaciones anteriores se pueden reescribir como:

{V}_{1}={n}_{1}\frac{d\mathrm{\Phi }}{dt}

{V}_{2}={n}_{2}\frac{d\mathrm{\Phi }}{dt}

Despejamos en cada una a \frac{d\mathrm{\Phi }}{dt} .

\frac{d\mathrm{\Phi }}{dt}=\frac{{V}_{1}}{{n}_{1}}

\frac{d\mathrm{\Phi }}{dt}=\frac{{V}_{2}}{{n}_{2}}

Igualamos las ecuaciones.

\frac{{V}_{1}}{{n}_{1}}=\frac{{V}_{2}}{{n}_{2}}

Agrupando FEM de un lado y número de espiras de otro nos queda:

\frac{{V}_{1}}{{V}_{2}}=\frac{{n}_{1}}{{n}_{2}}

Para dos bobinas perfectamente acopladas, el cociente de las FEM es igual al cociente del número de espiras en cada una. Esta sencilla relación que hemos encontrado se denomina relación de transformación y se utiliza en sistemas eléctricos de potencia para describir a los transformadores.

La respuesta correcta es el inciso d).

Reactivo 48

Suponga que tiene en sus manos un artefacto capaz de alterar las constantes universales y, en un momento dado, cuadruplica el valor de la permeabilidad magnética del vacío, ¿qué sucede con la velocidad de la luz en el vacío?

1. Se reduce a la mitad
2. Aumenta el doble
3. Permanece constante
4. Se reduce a una cuarta parte

Solución:

Unos de los resultados que se obtienen al estudiar las ondas electromagnéticas a partir de las ecuaciones de Maxwell, es que la rapidez con la que viajan a través del vacío, depende de la permeabilidad magnética y la permitividad eléctrica del vacío.

c=\frac{1}{\sqrt{{\mu }_{o}{ϵ}_{o}}}

Ahora, si cambiamos el valor de la permeabilidad magnética de tal forma que {\mu }_{o}^{\text{'}}=4{\mu }_{o} y sustituimos nos queda:

{c}^{\text{'}}=\frac{1}{\sqrt{4{\mu }_{o}{ϵ}_{o}}}=\frac{1}{2}\frac{1}{\sqrt{{\mu }_{o}{ϵ}_{o}}}

Sustituimos \frac{1}{\sqrt{{\mu }_{o}{ϵ}_{o}}} por c .

{c}^{\text{'}}=\frac{1}{2}c

Si la permitividad magnética del vacío se cuadruplica, la velocidad de la luz disminuye a la mitad.

Concluimos seleccionando como respuesta correcta al inciso a).

Reactivo 49

Si se toma un imán natural y se corta a la mitad, ¿cómo se comporta el campo magnético en los dos nuevos imanes?

1. Cada uno actúa como un monopolo magnético
2. Se convierten en imanes independientes
3. Pierden sus propiedades magnéticas
4. El campo magnético permanece invariante

Solución:

Los imanes permanentes fueron los primeros elementos que permitieron al hombre experimentar la interacción magnética de la materia. Una de sus características fundamentales, es que, sin importar cuántas veces se divida un imán, los trozos resultantes se comportan también como imanes, con sus respectivos, polo norte y sur.

Esto permite llegar a una conclusión acerca de las interacciones electromagnéticas: no existen monopolos magnéticos en la naturaleza. Concluimos indicando como respuesta correcta al inciso b).

Reactivo 50

Calcule la carga eléctrica encerrada por una esfera de radio r=4 \mathrm{c}\mathrm{m} , si a través de la misma se registra un flujo eléctrico de 2\times {10}^{-3}\frac{{\mathrm{N}\cdot \mathrm{m}}^{2}}{\mathrm{C}} . Tenga en cuenta que {ϵ}_{o}=9\times {10}^{-12}\frac{{\mathrm{C}}^{2}}{{\mathrm{N}\cdot \mathrm{m}}^{2}} .

1. 1.8\times {10}^{-15} \mathrm{C}
2. 0.18\times {10}^{-15} \mathrm{C}
3. 18\times {10}^{-15} \mathrm{C}
4. 18\times {10}^{-16} \mathrm{C}

Solución:

Para resolver este problema, debemos aplicar la Ley de Gauss para el electromagnetismo.

{\mathrm{\Phi }}_{e}=\frac{{Q}_{enc}}{{ϵ}_{o}}

El flujo eléctrico a través de una superficie cerrada, es igual a la carga neta en su interior dividida la permitividad eléctrica del vacío.

El enunciado nos indica el valor del flujo eléctrico, solo debemos despejar la carga eléctrica encerrada.

{Q}_{enc}={ϵ}_{o}\cdot {\mathrm{\Phi }}_{e}

Sustituimos.

{Q}_{enc}=\left(9\times {10}^{-12}\frac{{\mathrm{C}}^{2}}{{\mathrm{N}\cdot \mathrm{m}}^{2}}\right)\left(2\times {10}^{-3}\frac{{\mathrm{N}\cdot \mathrm{m}}^{2}}{\mathrm{C}}\right)=18\times {10}^{-15} \mathrm{C}

La carga eléctrica encerrada es de 18\times {10}^{-15} \mathrm{C} .

La respuesta correcta es el inciso c).