¡Hola aspirante! En este tutorial vamos a resolver los primeros 10 ejercicios del Examen Simulacro de Física para las carreras del área de Ciencias Médico Biológicas del Instituto Politécnico Nacional.
En total vamos a resolver 50 ejercicios de temas oficiales de la nueva guía de estudio del IPN.

Con este examen simulador y siguiendo las recomendaciones que te dejo en las siguientes secciones, podrás practicar las antes de la prueba real.
Además, es importante que leas el siguiente resumen con los puntos clave del examen al IPN y más adelante te explicaremos los cambios que han realizado en la prueba de ingreso con respecto a años anteriores.
- Carreras ofertadas en IPN: 70+
- Porcentaje de aceptación: 20%
- Preguntas en el examen de admisión: 140 preguntas
- Nuevos temas: Historia e Inglés (reading comprehension)
- Tipo: selección múltiple
Estructura Examen IPN
El examen para ingresar al IPN está compuesta de dos bloques, conocimientos generales y conocimientos experimentales.
Las materias en el bloque de conocimientos generales son las mismas para todas las carreras del IPN e incluye:
- Matemáticas
- Competencia escrita
- Competencia lectora
- Reading comprehension (nuevo tema)
- Historia
Por su parte, el bloque de conocimientos experimentales abarca las siguientes materias:
- Biología
- Química
- Física
La cantidad de reactivos dependerá de la rama de conocimiento a la que pertenece la carrera que deseas estudiar. Ellas se dividen en:
- IyCFM: Ingeniería y ciencias físico matemáticas
- CMD: Ciencias médico biológicas
- CSyA: Ciencias sociales y administrativas
La siguiente tabla muestra la estructura de reactivos por materia para cada área:
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Cuáles son los cambios del examen de ingreso al IPN? Por si aún tienes dudas te dejamos un resumen con los puntos más resaltantes a los que debes prestar atención:
- El examen evaluará la materia de inglés, específicamente en el tema de Reading comprehension.
- Las materias de competencia escrita y competencia lectora, sustituyeron a producción escrita y comprensión de textos.
- Cada área asigna la cantidad de reactivos por materia.
- Se agregó la materia de historia de México a las tres áreas de estudio.
- El examen para todas las carreras tendrá 140 reactivos (anteriormente eran 130).
Temario Física CMB
A continuación, te dejo una lista con todos los temas de física que deberás estudiar para quedar seleccionado:
- Sistemas de unidades y mediciones.
- Álgebra vectorial.
- Estática.
- Cinemática y dinámica.
- Propiedades generales de la materia.
- Mecánica de fluidos.
- Termodinámica.
- Acústica.
- Electricidad.
- Electromagnetismo.
- Electroinducción-Ondas electromagnéticas.
- Óptica.
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Incluye exámenes simulacro en tu rutina de estudio, de esa forma pondrás a prueba tus conocimientos en condiciones similares a la prueba real y alcanzar los aciertos que necesitas por carrera.
Las siguientes, son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve cada parte (I, II y III) por tu cuenta antes de checar las respuestas.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
Reactivo 1
Dados los vectores \overrightarrow{u}=\left(1, 3, 5\right) y \overrightarrow{v}=\left(-1, 0, 1\right) , calcule el producto escalar entre ellos.
- 4
- -1
- -4
- 1
Solución:
Para calcular el producto escalar entre dos vectores, debemos realizar el producto, coordenada a coordenada entre los vectores y sumarlos entre sí.
Fórmula para el producto escalar entre vectores en {\mathrm{R}}^{3} .
\left({a}_{1}, {a}_{2}, {a}_{3}\right)\cdot \left({b}_{1}, {b}_{2}, {b}_{3}\right)={a}_{1}{b}_{1}+{a}_{2}{b}_{2}+{a}_{3}{b}_{3}
Recordemos además que el producto escalar es conmutativo, por tanto, no importa el orden. Aplicamos la fórmula anterior en los vectores dados:
\overrightarrow{u}\cdot \overrightarrow{v}=\left(1, 3, 5\right)\cdot \left(-1, 0, 1\right)=\left(1\right)\left(-1\right)+\left(3\right)\left(0\right)+\left(5\right)\left(1\right)
Resolviendo nos queda:
\overrightarrow{u}\cdot \overrightarrow{v}=-1+0+5=4
Concluimos el problema indicando como respuesta correcta al inciso a).
Reactivo 2
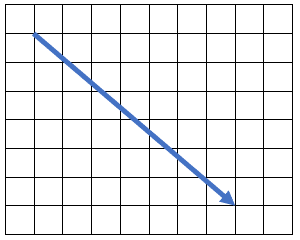
A partir de la siguiente representación gráfica del vector \overrightarrow{A} en el plano, expréselo a partir de los vectores unitarios de x y y . Tenga en cuenta que la distancia de cada rectángulo es de 1 unidad.
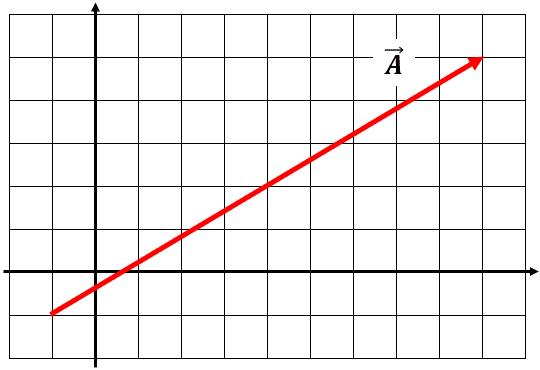
- -10\widehat{i}-6\widehat{j}
- -10\widehat{i}+6\widehat{j}
- 10\widehat{i}-6\widehat{j}
- 10\widehat{i}+6\widehat{j}
Solución:
Para encontrar la forma canónica del vector, simplemente debemos extraer las coordenadas del punto inicio y extremo a partir de la imagen y luego expresarlas según los vectores unitarios \widehat{i} y \widehat{j} .
Sobre la figura, identificamos el inicio y extremo del vector como:
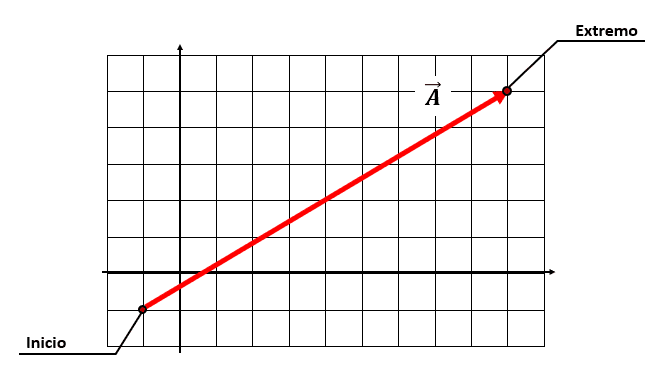
Si cada una de los recuadros mide 1 unidad de longitud, el inicio y extremo quedarían como:
\mathrm{I}\mathrm{n}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{o}:\mathrm{ }{P}_{i}=\left(-1, -1\right)
\mathrm{E}\mathrm{x}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{o}:{P}_{e}=\left(9, 5\right)
Las coordenadas del vector de calculan con la siguiente fórmula:
\overrightarrow{A}=\left({x}_{e}-{x}_{i}, {y}_{e}-{y}_{i}\right)
Sustituimos en la ecuación.
\overrightarrow{A}=\left(9+1, 5+1\right)=\left(10, 6\right)
Expresamos al vector en su forma canónica:
\overrightarrow{A}=10\widehat{i}+6\widehat{j}
Comparando con los incisos, la respuesta correcta está en el d).
Reactivo 3
Una alberca de 3000 metros cúbicos de capacidad, planea llenarse con una bomba hidráulica que tiene como caudal máximo de salida 200 litros por minuto. Si un litro equivale a 0.001 metros cúbicos, ¿en cuántos minutos se llenará la alberca?
- 15,000
- 14,000
- 150,000
- 140,000
Solución:
En este caso, debemos comenzar por identificar la variable desconocida, en nuestro caso, el tiempo que tarda en llenarse la alberca. Esto lo podemos calcular al dividir el volumen total de la alberca con el caudal de la bomba, pero, es necesario convertir los 3000 metros cúbicos en litros o los 200 litros en metro cúbicos.
Esta vez, convertiremos los 3000 metros cúbicos a litros.
\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{a}=3000\mathrm{ }{\mathrm{m}}^{3}\cdot \frac{1 \mathrm{l}\mathrm{t}}{0.001 {\mathrm{m}}^{3}}=3000000 \mathrm{l}\mathrm{t}
Ahora, calculamos el tiempo de llenado dividiendo el volumen en litros por el caudal de la bomba.
\mathrm{T}\mathrm{i}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{d}\mathrm{o}=\frac{3000000 \mathrm{l}\mathrm{t}}{200 \mathrm{l}\mathrm{t}/\mathrm{m}\mathrm{i}\mathrm{n}}=15000 \mathrm{m}\mathrm{i}\mathrm{n}
La alberca se tardaría 15,000 minutos en llenarse por completo.
Comparando con los incisos, la respuesta correcta está en el a).
Reactivo 4
A partir de la máquina de Atwood que se muestra en la figura, determine el valor de la masa {m}_{1} para que el sistema sea estático. Tenga en cuenta el valor de la gravedad g=9.8 \mathrm{m}/{\mathrm{s}}^{2} , la masa {m}_{2}=10 \mathrm{k}\mathrm{g} y que la rampa inclinada no tiene fricción con la masa 1.
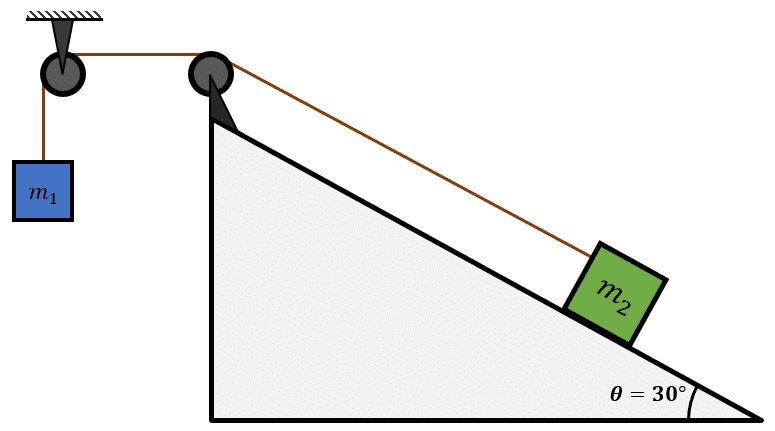
- 12 kg
- 10 kg
- 8 kg
- 5 kg
Solución:
Para resolver cualquier problema de estática, lo primero que debemos identificar es el tipo de sistema que estamos analizando y la cantidad de cuerpos que conforman al sistema. En este caso, tenemos a dos bloques unidos por una cuerda, una cuelga libremente y la otra se encuentra sobre el plano inclinado.
Comenzamos realizando el diagrama de cuerpo libre de la masa 1.
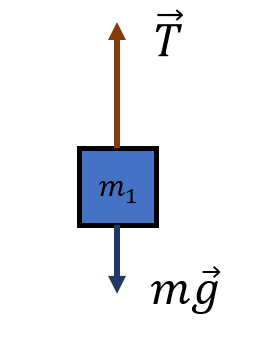
Para la primera masa, solo tenemos dos fuerzas: la fuerza de gravedad y la tensión de la cuerda. Aplicando la primera condición de estática sobre el eje y :
\sum {F}_{y}=0\to T-{m}_{1}g=0
En este caso, para mantener el equilibrio la tensión de la cuerda debe ser igual al peso de la masa 1.
T={m}_{1}g
Vamos con el DCL para la masa 2.
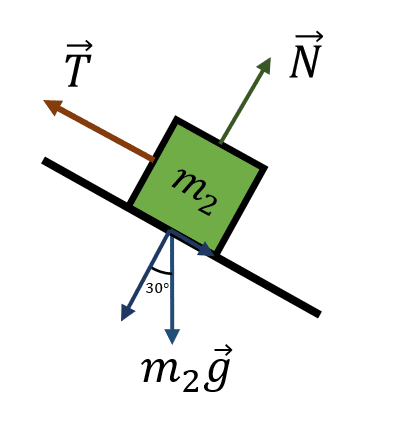
Debido a que la rampa se encuentra inclinada, el peso de la masa 2 se descompone en las direcciones x y y como:
\begin{array}{c}{P}_{2x}={m}_{2}g\mathrm{sin}30\\ {P}_{2y}={m}_{2}g\mathrm{cos}30\end{array}
Para este bloque deberíamos realizar la descomposición de fuerzas tanto en x como en y , pero debido a que solo se podría desplazar en x y, además, la tensión de actúa en dicha dirección, sólo nos importa el equilibrio en esta componente.
\sum {F}_{x}=0\to {m}_{2}g\mathrm{sin}30-T=0
Despejamos la tensión de la cuerda:
T={m}_{2}g\mathrm{sin}30
Igualamos esta ecuación con T={m}_{1}g para, finalmente, calcular a {m}_{1} .
T={m}_{1}g={m}_{2}g\mathrm{sin}30\to {m}_{1}={m}_{2}\mathrm{sin}30
Sustituimos {m}_{2}=10 \mathrm{k}\mathrm{g} y \mathrm{sin}30=0.5 .
{m}_{1}=\left(10 \mathrm{k}\mathrm{g}\right)\left(0.5\right)=5 \mathrm{k}\mathrm{g}
Para lograr el equilibrio según la primera ley de Newton, la masa {m}_{1} debe ser igual a 5 kilogramos.
Comparando con los incisos, seleccionamos como correcto al d).
Reactivo 5
Calcule el volumen que tiene un cilindro de radio igual a 0.5 metros y altura 3 metros. Considere que 1 litro es igual a 0.001 metros cúbicos.
- 2500 lt
- 2450 lt
- 2356 lt
- 2247 lt
Solución:
Para calcular el volumen de un cilindro, podemos utilizar la siguiente ecuación:
{V}_{c}=\pi {r}^{2}h
Donde r es el radio y h la altura del cilindro. Sustituimos en la ecuación:
{V}_{c}=\pi {\left(0.5\right)}^{2}\left(3\right)=2.356 {\mathrm{m}}^{3}
Ahora, debemos transformar los metros cúbicos a litros.
{V}_{c}=2.356 {\mathrm{m}}^{3}\cdot \frac{1 \mathrm{l}\mathrm{t}}{0.001 {\mathrm{m}}^{3}}=2356 \mathrm{l}\mathrm{t}
El cilindro tiene un volumen total de 2356 litros.
La respuesta correcta es la opción c).
Reactivo 6
Dado el vector \overrightarrow{u}=\left(6, -3\right) , identifique cuál de las siguientes representaciones le corresponde.
Solución:
Recordemos que los vectores no responden a unas coordenadas en el plano o en el espacio según sea el caso, por el contrario, a los vectores podríamos entenderlos como desplazamientos que ocurren sobre los ejes coordenados y cuya magnitud corresponde a las componentes del vector.
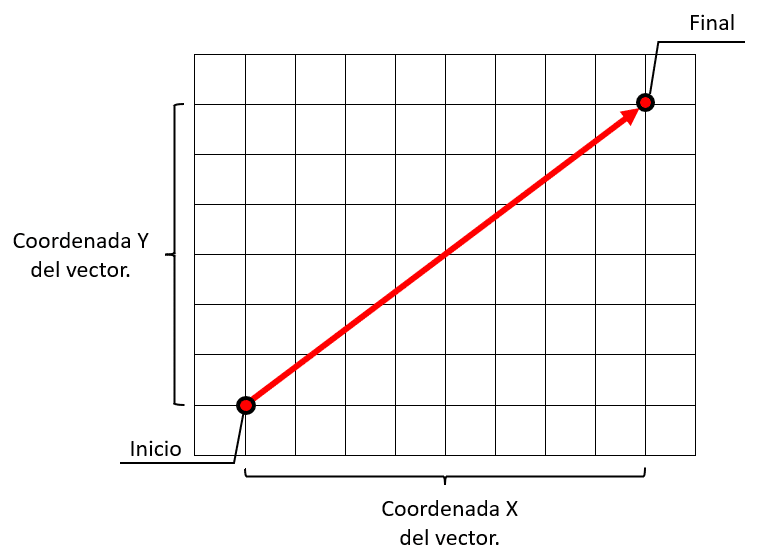
Recordando esto, solo debemos identificar al vector de los incisos que tiene como ordenada un desplazamiento de +6 y como abscisa un desplazamiento de -3 (hacia abajo).
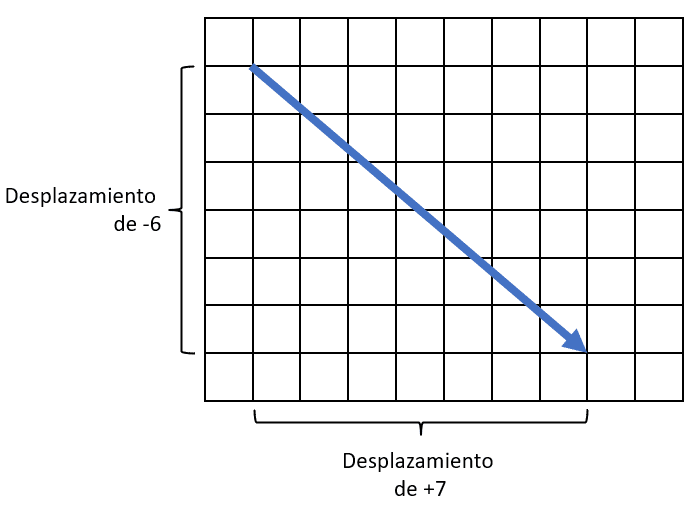
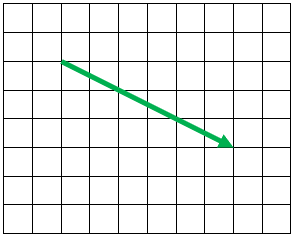
El primer vector tiene un desplazamiento de +7 en la horizontal y de -6 en la vertical. No corresponde al vector \overrightarrow{u} .
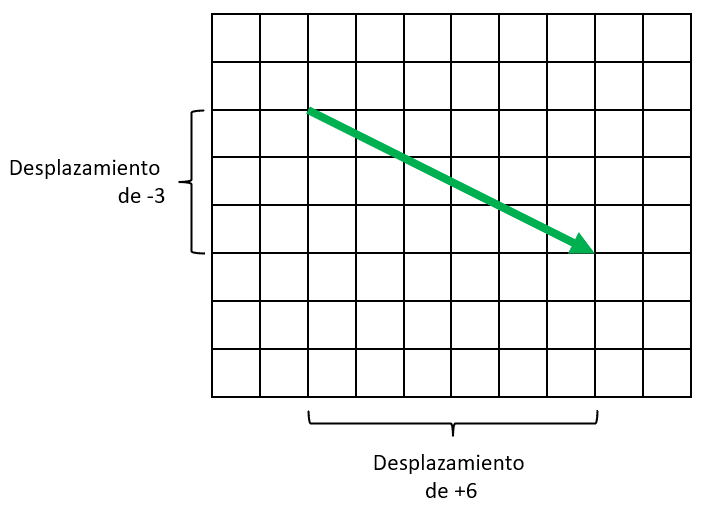
El primer vector tiene un desplazamiento de +6 en la horizontal y de -3 en la vertical. Este si corresponde al vector \overrightarrow{u} .
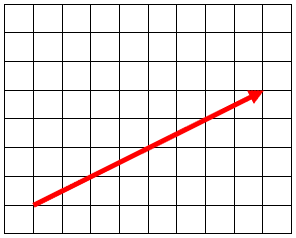
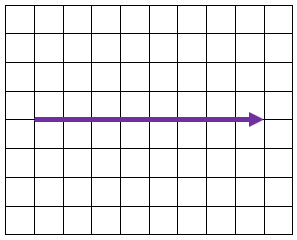
Los otros dos vectores rotundamente no pueden ser un equivalente para \overrightarrow{u} ya que el primero apunta hacia arriba y el segundo no tiene desplazamiento vertical. Concluimos indicando como correcta la b).
Reactivo 7
Dado el vector en el plano \overrightarrow{v}=\left(3, 5\right) , determine el coseno del ángulo que forma con el vector \overrightarrow{u}=\left(1, -1\right) .
- -\frac{1}{\sqrt{17}}
- \frac{1}{\sqrt{17}}
- \frac{2}{\sqrt{17}}
- -\frac{2}{\sqrt{17}}
Solución:
Este problema podríamos resolverlo mediante diferentes enfoques: encontrando las rectas que pasan por los vectores, aplicando trigonometría o, de forma netamente vectorial aplicando la definición de producto escalar.
Debido a su versatilidad y que, en este caso es la mejor opción, emplearemos la definición de producto escalar.
\overrightarrow{v}\cdot \overrightarrow{u}=\left|\overrightarrow{v}\right|\left|\overrightarrow{u}\right|\mathrm{cos}\theta
Despejamos al coseno de theta.
\mathrm{cos}\theta =\frac{\overrightarrow{v}\cdot \overrightarrow{u}}{\left|\overrightarrow{v}\right|\left|\overrightarrow{u}\right|}
Ahora solo nos queda encontrar el producto punto y el módulo de ambos vectores.
\overrightarrow{v}\cdot \overrightarrow{u}=\left(3, 5\right)\cdot \left(1, -1\right)=\left(3\right)\left(1\right)+\left(5\right)\left(-1\right)=3-5=-2
\left|\overrightarrow{v}\right|=\sqrt{{3}^{2}+{5}^{2}}=\sqrt{34}
\left|\overrightarrow{u}\right|=\sqrt{{1}^{2}+{\left(-1\right)}^{2}}=\sqrt{2}
Sustituimos.
\mathrm{cos}\theta =\frac{-2}{\sqrt{34}\cdot \sqrt{2}}=-\frac{2}{\sqrt{68}}
Simplificando nos queda:
\mathrm{cos}\theta =-\frac{1}{\sqrt{17}}
Comparando con los incisos, el correcto es a).
Reactivo 8
¿Cuál debe ser el valor de la masa {m}_{2} para que el sistema permanezca en equilibrio?
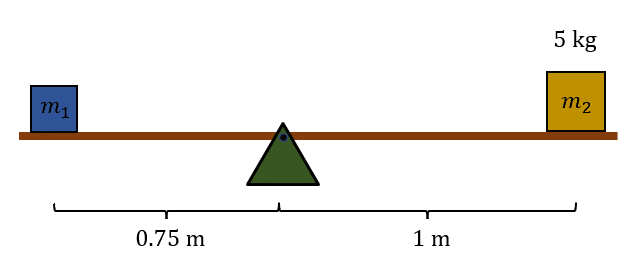
- 45 kg
- 5 kg
- 5 kg
- 66 kg
Solución:
Para resolver este problema, debemos emplear la segunda condición de estabilidad mecánica: la sumatoria de todos los torques alrededor de un mismo eje de rotación es igual a cero.
\sum \overrightarrow{\tau }=0
Para armar las ecuaciones en el caso de torcas, debemos definir un sentido de giro positivo, para nosotros serán las torcas que provocan giros en sentido antihorario. Por otra parte, recordemos que una torca se calcula como:
\tau =rF
Donde r es la distancia entre el eje de rotación y el cuerpo que gira y F es la magnitud de la fuerza. En este caso, la fuerza responsable de las torcas es el peso de cada bloque:
{F}_{1}={m}_{1}g, F{}_{2}={m}_{2}g
Siguiendo la convención establecida para las torcas, la masa {m}_{1} genera una {\tau }_{1} en sentido positivo y {m}_{2} otra {\tau }_{2} en sentido negativo.
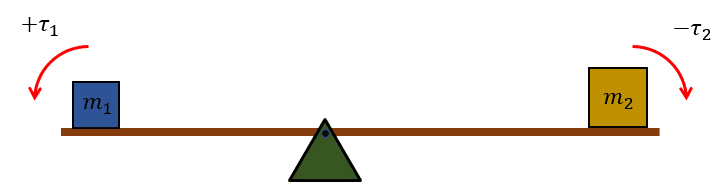
{\tau }_{1}-{\tau }_{2}=0
Sustituimos:
{r}_{1}{m}_{1}g-{r}_{2}{m}_{2}g=0
Despejamos la masa {m}_{1} .
{m}_{1}=\frac{{r}_{2}{m}_{2}}{{r}_{1}}
Sustituimos:
{m}_{1}=\frac{\left(1 \mathrm{m}\right)\left(5 \mathrm{k}\mathrm{g}\right)}{0.75 \mathrm{k}\mathrm{g}}=6.66 \mathrm{k}\mathrm{g}
La masa {m}_{1} debe ser de 6.66 kilogramos para lograr la estabilidad mecánica.
La respuesta correcta es el inciso d).
Reactivo 9
Josué es el encargado del laboratorio de física aplicada en un centro de investigación. La directiva acaba de adquirir un nuevo instrumento para realizar mediciones sobre la velocidad de los fluidos en diferentes formas y canales.
Si el instrumento indica las mediciones en \mathrm{c}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n} , ¿cuál sería la constante de proporcionalidad para transformar la medición al sistema internacional de unidades?
- \frac{1}{6000}
- \frac{1}{600}
- \frac{1}{60}
- \frac{1}{6}
Solución:
Aunque el enunciado del problema parezca bastante largo, solo debemos encontrar un factor de conversión de \mathrm{c}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n} a \mathrm{m}/\mathrm{s} , que es la unidad de velocidad según el sistema internacional.
Diremos que y es la velocidad en \mathrm{m}/\mathrm{s} y x la velocidad en \mathrm{c}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n} . Además, sabemos que un metro es igual a 100 cm y que 1 minuto es igual a 60 segundos.
y=x\frac{\mathrm{c}\mathrm{m}}{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \frac{1 \mathrm{m}\mathrm{i}\mathrm{n}}{60 \mathrm{s}}\cdot \frac{1 \mathrm{m}}{100 \mathrm{c}\mathrm{m}}=\frac{x}{6000}\frac{\mathrm{m}}{\mathrm{s}}\mathrm{ }
La constante de proporcionalidad entre \mathrm{c}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n} y \mathrm{m}/\mathrm{s} es \frac{1}{6000} .
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 10
Calcule la masa que debe tener el bloque azul para que el sistema permanezca en equilibrio, tal como se muestra en la figura.
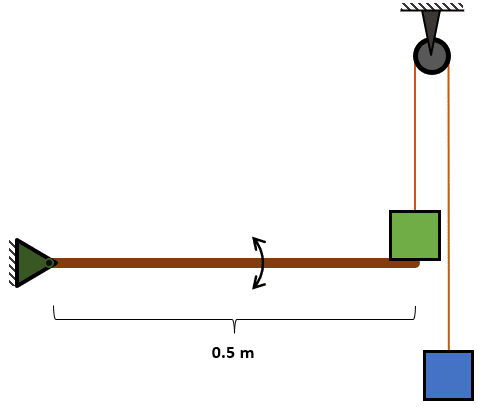
- {m}_{v}=2{m}_{a}
- {m}_{a}=2{m}_{v}
- {m}_{a}=\frac{1}{3}{m}_{v}
- {m}_{a}={m}_{v}
Solución:
Aunque este problema parezca complejo por su configuración, tenemos algunas salvedades que se simplifican un montón. Primero, nos preguntan la masa azul para un ángulo de inclinación de la barra igual a cero, es decir, la misma estará totalmente erguida, esto evita la descomposición de fuerzas según un ángulo.
Por otra parte, podemos asumir que la torca y la tensión de la cuerda ocurren en el mismo punto, esto simplifica el análisis al momento de hacer balance de torcas. Comencemos con el bloque más sencillo: el que se encuentra suspendido en el aire.
Para lograr equilibrio en él, la sumatoria de fuerzas debe ser igual a cero.
\sum {F}_{y}=0\to T-{m}_{a}g=0
Despejamos la tensión de la cuerda:
T={m}_{a}g
Ahora, aplicamos balance de torcas sobre el brazo suspendido. Sobre la barra hay dos torcas: una debido a la masa verde y otra debido a la tensión de la cuerda. Asumimos como positivos las torcas en sentido antihorario.
\sum \tau =0\to rT-r{m}_{v}g=0
T={m}_{v}g
Igualando las ecuaciones:
{m}_{v}g={m}_{a}g
Finalmente:
{m}_{v}={m}_{a}
Las masas deben ser iguales para que el sistema permanezca en equilibrio.
Concluimos que la respuesta correcta es la d).