¡Hola de nuevo aspirante! En este post estaremos desarrollando los reactivos de física de la guía UANL 2021 para el examen de ingreso. Recuerda intentar hacerlos por tu cuenta, luego regresa para revisar el procedimiento y verificar tus resultados.

La prueba de admisión a la Universidad Autónoma de Nuevo León, diseñada por la Pearson, consta de dos partes. A continuación, tienes un resumen de la convocatoria:
- Períodos de ingreso: Dos al año.
- Inicio de registro: Abril y Octubre
- Carreras ofertadas: 100+
- Examen de admisión: Pearson
- Porcentaje de Aceptación: 50%
Estructura del examen de la UANL
La primera parte, llamada conocimientos generales es igual para todos los aspirantes y se compone de análisis matemático, comprensión lectora y lingüística. En la segunda, los conocimientos por área dependen de la facultad a la que desees ingresar.
La siguiente tabla es un resumen con las áreas, cantidad de reactivos y el tiempo para resolverlos.
| Partes del examen | Áreas | Reactivos | Tiempo |
|---|---|---|---|
| Primera | Pensamiento matemático y analítico | 50 | 90 |
| Estructura de la lengua y comprensión lectora | 50 | 90 | |
| Segunda | Inglés | 20 | 20 |
| Comprensión lectora | 20 | 30 | |
| Área de conocimiento 1 | 20 | 20 | |
| Área de conocimiento 2 | 20 | 20 | |
| Totales | 180 | 270 |
Como puedes ver, el examen tiene una duración de 4 horas y media. No sólo tienes que dominar los temas de ambas partes, también debes conseguir el mejor tiempo para acumular el puntaje que exige la carrera.
Temario del Área de Física
La variedad de los temas en el área de física van desde el álgebra vectorial, pasando por mecánica clásica, electricidad y magnetismo, hasta óptica y física cuántica. A continuación, mira la lista exacta del contenido que debes estudiar.
Fundamentos teórico-prácticos
- Sistemas de unidades y conversiones
- Suma y resta de vectores
Mecánica
- Equilibrio estático
- Movimiento rectilíneo uniforme y uniformemente acelerado
- Movimiento circular uniforme
- Leyes de Newton: aplicaciones y tipos de fricción
- Trabajo, potencia y energía mecánica
- Presión hidrostática, principio de Arquímedes, principio de Pascal
Calor y termodinámica
- Calor y temperatura
- Transmisión del calor
- Variables termodinámicas: masa, volumen, densidad, presión y temperatura
- Leyes de la termodinámica: primera, segunda y cero
Electricidad
- Carga eléctrica y ley de Coulomb
- Corriente eléctrica y ley de Ohm
- Potencia eléctrica y el efecto Joule
- Circuitos eléctricos
Interacción de la materia y la energía
- Electromagnetismo
Óptica y acústica
- Reflexión y refracción de la luz
- Ondas longitudinales y transversales
Guía UANL de Física resuelta
Ahora, vamos con los 10 reactivos de física resueltos paso a paso, para el examen de ingreso a la Universidad Autónoma de Nuevo León.
Reactivo 1: Vectores
Relaciona las siguientes columnas según corresponda.

- 1a, 2b, 3c
- 1b, 2c, 3a
- 1c, 2a, 3b
- 1c, 2b, 3a
Solución:
Para relacionar correctamente los incisos de cada columna, debemos saber cuál es la diferencia entre magnitud y cantidad física.
Las cantidades, son porciones de una magnitud, es decir, se les ha asociado una cualidad física, entiéndase: una magnitud.
Por otro lado, las magnitudes corresponden a cualidades capaces de representar un tipo de interacción o propiedad intrínseca de la naturaleza que nos rodea.
Existen magnitudes escalares y vectoriales. Los escalares representan sólo un número, mientras que los vectores (y otros objetos matemáticos) permiten simbolizar magnitudes más complejas que poseen magnitud y sentido.
- Ejemplos de magnitudes escalares: temperatura, tiempo, masa, volumen, densidad.
- Ejemplos de magnitudes vectoriales: fuerza, presión, campo eléctrico, velocidad.
En base a lo anterior, podemos relacionar fácilmente los incisos de la columna izquierda con su correspondiente en la columna derecha.
Vector: Magnitud física definida en un sistema de referencia que se caracteriza por tener magnitud, dirección y sentido.
1c.
Cantidad vectorial: Cantidad física que está completamente determinada por su magnitud, dirección y sentido.
2a.
Cantidad escalar: Cantidad física que está completamente determinada por un número y la correspondiente unidad.
3b.
Combinando las respuestas nos queda: 1c, 2a, 3b. La opción correcta es la c).
Reactivo 2: Gráfica de posición vs tiempo
Observa la siguiente gráfica.
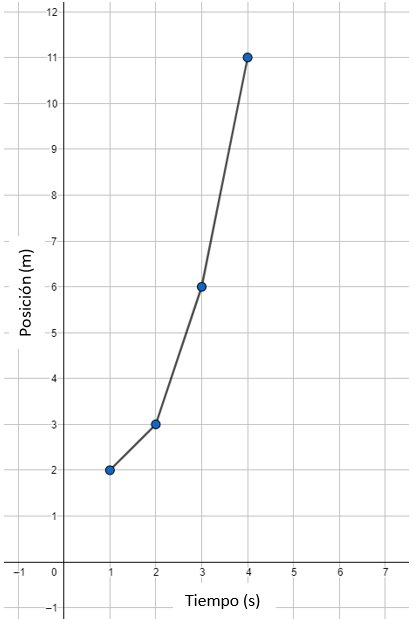
¿Cuál es la velocidad media del movimiento descrito en la gráfica?
- 3\frac{m}{s}
- 9\frac{m}{s}
- 3\frac{m}{{s}^{2}}
- 9\frac{m}{{s}^{2}}
Solución:
La velocidad lineal media (asumiendo que la trayectoria del cuerpo es recta) en un intervalo de tiempo es el cociente entre el desplazamiento recorrido durante el intervalo considerado entre los puntos 1 y 2, y la duración de este. Es decir:
{v}_{m}=\frac{{s}_{2}-{s}_{1}}{{t}_{2}-{t}_{1}}
Donde:
- {s}_{1} y {s}_{2} son las posiciones en los puntos
- {t}_{1} y {t}_{2} es el tiempo en los puntos escogidos
En el caso de la gráfica, debemos calcular la velocidad media de todo el recorrido. Examinado el punto inicial y final de la curva, sabemos que:
{t}_{1}=1 s;{s}_{1}=2 m
{t}_{2}=4 s;{s}_{2}=11 m
Sustituimos en la ecuación de velocidad media.
{v}_{m}=\frac{11-2}{4-1}=\frac{9}{3}=3\frac{m}{s}
Concluimos que la respuesta correcta es el inciso a).
Reactivo 3: Movimiento Uniformemente Acelerado
Un automóvil que parte del reposo, acelera uniformemente y alcanza una velocidad de 7.5\frac{m}{s} en 5 s. Suponiendo que mantiene esa misma aceleración, ¿Cuánto tiempo más tiene que pasar para que el automóvil alcance una velocidad de 10.5\frac{m}{s} ?
- 1.5 s
- 3 s
- 5 s
- 2 s
Solución:
Para resolver problemas de cinemática, debemos identificar los puntos iniciales y finales de cada intervalo. En este caso, tenemos a un cuerpo que parte del reposo, es decir, la velocidad inicial es {v}_{1}=0\frac{m}{s} en {t}_{1}=0 s .
Pasados 5 segundos, {t}_{2}=5 s , el cuerpo se ha movido con aceleración constante, alcanzando una velocidad de {v}_{2}=7.5\frac{m}{s} . Luego, el cuerpo se mantiene con la misma aceleración y, dado cierto tiempo {t}_{3} , alcanza una velocidad {v}_{3}=10.5\frac{m}{s} .
La aceleración se puede calcular con los datos del intervalo 1-2.
a=\frac{{v}_{2}-{v}_{1}}{{t}_{2}-{t}_{1}}
Sustituimos los valores.
a=\frac{7.5-0}{5-0}=1.5 m/s
Ahora, con el intervalo 2-3 podemos calcular el tiempo que transcurre \Delta {t}_{23} hasta que alcanza {v}_{3}=10.5\frac{m}{s} .
a=\frac{{v}_{3}-{v}_{2}}{{t}_{3}-{t}_{2}}=\frac{{v}_{3}-{v}_{2}}{\Delta {t}_{23}}
Despejamos a \Delta {t}_{23} y sustituimos los valores.
\Delta {t}_{23}=\frac{{v}_{3}-{v}_{2}}{a}=\frac{10.5-7.5}{1.5}=2 s
Transcurren 2 segundos hasta que el cuerpo alcanza una velocidad de 10.5\frac{m}{s} .
La respuesta correcta es la d).
Reactivo 4: Movimiento Circular Uniforme
Una niña corre en una pequeña pista circular de 10 m de radio. La niña tarda 11.2 s en completar una vuelta, entonces, ¿Cuál es el periodo del movimiento, la frecuencia y la rapidez lineal de la niña?
- 0.089s,11.2Hz,5.61\frac{m}{s}
- 11.2s,0.089Hz,5.61\frac{m}{s}
- 11.2s,5.61Hz,0.089\frac{m}{s}
- 5.61s,0.089Hz,11.2\frac{m}{s}
Solución:
El movimiento circular uniforme es aquel en el que siguiendo la trayectoria circular de un cuerpo alrededor de un punto fijo central, la velocidad angular \omega (cambio del ángulo respecto del tiempo rad/s ) se mantiene constante.
En este caso, el tiempo que tarda la niña en completar el recorrido es el periodo del movimiento circular \tau =11.2 s . La frecuencia f es el inverso del periodo, cuya interpretación es: la cantidad de vueltas que da la niña en un segundo.
f=\frac{1}{\tau }=\frac{1}{11.2 s}=0.089 Hz
Existe una relación entre la rapidez lineal de la niña y la angular:
v=\omega r
Donde \omega es la velocidad angular que se calcula como:
\omega =\frac{2\pi }{\tau }
Sustituimos en la ecuación de rapidez lineal:
v=\frac{2\pi r}{\tau }
Evaluamos.
v=\frac{2\pi \left(10 m\right)}{11.2 s}=5.61\frac{m}{s}
Finalmente: 11.2s,0.089Hz,5.61\frac{m}{s} .
Comparando con las opciones, la respuesta correcta es el inciso b).
Reactivo 5: Trabajo y potencia
Un bloque con una masa de 1.8 kg se coloca en la parte más alta de un plano inclinado a un ángulo de 24° respecto a la horizontal. Si el plano tiene una longitud de 4.7 m, y no existen fuerzas de fricción considerables entre el bloque y el plano. Encuentra el trabajo producido sobre el bloque y determina la potencia desarrollada.
- 33.76J,22.42W
- 22.42J,33.76W
- 36.76J,28.42W
- 28.42J,36.76W
Solución:
En este caso el enunciado nos dice que el bloque se encuentra en los más alto de un plano inclinado, por tanto, el trabajo es realizado por la gravedad para llevar al bloque hasta el punto más bajo. Hagamos un pequeño esbozo de la situación planteada.
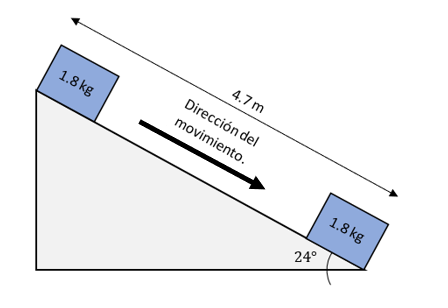
El trabajo mecánico, se calcula como el producto entre la fuerza efectiva aplicada sobre el cuerpo y el desplazamiento. El trabajo es positivo si la fuerza va en el mismo sentido que el desplazamiento y negativo en caso contrario.
W=F\Delta x
Para determinar la componente del peso que realiza trabajo, debemos hacer un DCL del bloque.
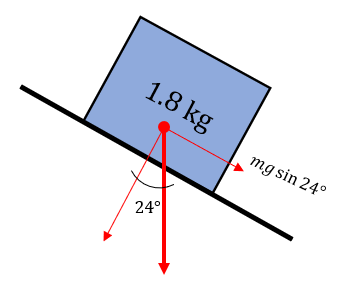
La componente que realiza trabajo y va en dirección al movimiento es:
{F}_{x}=mgsin 24
Sustituimos en la ecuación de trabajo.
W=mg\Delta xsin 24
Evaluamos la expresión.
W=\left(1.8\right)\left(9.81\right)\left(4.7\right)sin 24 =33.76 J
La potencia se calcula como el trabajo dividido por el tiempo que tomó llevarlo a cabo. En este caso, no sabemos cuánto tiempo le tomó a la componente de la gravedad llevar al bloque hasta la parte más baja, pero se puede calcular al obtener la componente de la aceleración de gravedad en dirección al movimiento.
{a}_{x}=gsin 24 =\left(9.81\right)sin 24 =4\frac{m}{{s}^{2}}
Ahora, calculamos el tiempo que ha tardado en desplazarse por el plano inclinado con la siguiente ecuación:
\Delta x={v}_{o}t+\frac{a}{2}{t}^{2}
Sustituimos.
4.7=\left(0\right)t+\frac{4}{2}{t}^{2}
2{t}^{2}=4.7\to t=1.505 s
Calculamos la potencia desarrollada con la siguiente ecuación:
P=\frac{W}{t}=\frac{33.76}{1.505}=22.42 W
Finalmente:
33.76J,22.42W
Comparando con las opciones, la respuesta correcta es la opción a).
Reactivo 6: Fuerza de Empuje
Un cuerpo con un volumen de 5\times {10}^{-4}{m}^{3} se sumerge en su totalidad en agua. Si la masa de dicho cuerpo es de 580 g, entonces: encuentra la magnitud de la fuerza de empuje que ejerce el agua sobre el cuerpo y determina si el cuerpo flota o se hunde en el agua.
- 4.9N,5.69N, sí flota.
- 5.69N,4.9N, sí flota.
- 4.9N,5.69N, no flota.
- 5.69N,4.9N, no flota.
Solución:
Al sumergir un cuerpo total o parcialmente en un líquido, podemos notar que el líquido desplazado empuja con una fuerza hacia arriba, provocando que el cuerpo experimente una pérdida aparente de peso dentro de la sustancia. Arquímedes fue quien notó que el peso del volumen de líquido desplazado es igual a la fuerza de empuje sobre el cuerpo.
E={\rho }_{s}{V}_{d}g
En este caso, como el cuerpo está totalmente sumergido, el volumen desplazado es igual al volumen del cuerpo.
{V}_{d}=5\times {10}^{-4}{m}^{3}
La densidad del agua líquida es 1000 kg/{m}^{3} . Sustituimos en la ecuación y calculamos el empuje.
E=\left(1000\frac{kg}{{m}^{3}}\right)\left(5\times {10}^{-4}{m}^{3}\right)\left(9.8\frac{m}{{s}^{2}}\right)=4.9 N
Para comprobar si el cuerpo flota, debemos calcular su peso. Si resulta menor al empuje, entonces el cuerpo flota, si no, está al fondo del recipiente.
w=mg=\left(0.58 kg\right)\left(9.8\frac{m}{{s}^{2}}\right)=5.69 N
El peso es mayor al empuje, por tanto: el cuerpo no flota.
Concluimos escogiendo al inciso c) como respuesta correcta.
Reactivo 7: Gases ideales
Durante una expansión isobárica, un gas contenido en un pistón incrementa su temperatura de 80° C hasta 135 °C. Si el volumen inicial del gas era de 850 ml, encuentra el volumen final del gas.
- 1300 ml
- 1250 ml
- 1400 ml
- 982.4 ml
Solución:
Para calcular el volumen de expansión isobárica (presión constante) del gas, debemos emplear una de las leyes relacionadas con los gases ideales. Específicamente, la ley de Charles-Gay Lussac, establece que, a presión constante, el volumen de un gas ideal es directamente proporcional a su temperatura y que el cociente de ambas propiedades es constante.
\frac{v}{T}=ctte\to v\propto T
De esta forma, si tenemos dos estados de un proceso isobárico de un gas ideal, podemos establecer la siguiente igualdad:
\frac{{v}_{1}}{{T}_{1}}=\frac{{v}_{2}}{{T}_{2}}
El problema nos indica cual es el volumen inicial {v}_{1}=850 ml , la temperatura inicial {T}_{1}=80 °C y la temperatura final {T}_{2}=135 °C . Debemos transformar la temperatura a kelvin porque la escala de temperatura debe ser absoluta. También deberíamos transformar el volumen a {m}^{3} , pero como el factor de conversión es un producto, hace que estos cálculos permanezcan inalterados.
{T}_{1}=353.15 K
{T}_{2}=408.15 K
Despejamos y sustituimos:
{v}_{2}=\frac{{T}_{2}}{{T}_{1}}{v}_{1}=\frac{408.15 K}{353.15 K}\left(850 ml\right)=982.4 ml
Comparando con las opciones, la respuesta correcta es el inciso d).
Reactivo 8: Efecto Joule
Un cable de cobre libera 870 000 cal de calor después de estar conectado a una fuente de voltaje de 200 V durante 50 minutos. ¿Cuál es el valor de la intensidad de la corriente que pasa por el cable?
- 6.96 A
- 5.40 A
- 6.04 A
- 5.08 A
Solución:
En este problema, debemos analizar la situación desde dos esquemas diferentes de la física. Por un lado, la electricidad, que nos dice que la potencia disipada en forma de calor por una resistencia eléctrica es igual al producto entre el voltaje aplicado y la corriente que circula por ella.
P=VI
Y por otro, la termodinámica nos dice que la energía en un sistema aislado se conserva. El calor transferido o disipado es igual al trabajo realizado más la variación de energía interna.
Q=W+\Delta U
En este caso no hay variación de energía interna, la expresión queda:
Q=W
Ya que nuestro sistema aislado es el cable, podemos sustituir la función que define cómo se da la disipación de potencia en él, multiplicado por el tiempo.
Q=VIt
Despejamos a la corriente.
I=\frac{Q}{tV}
Convertimos el tiempo a segundos y el calor a Joules.
t=50 min\bullet \frac{60 s}{1 min}=3000 s
Q=870000 cal\bullet \frac{4.165 J}{1 cal}=3623550 J
Calculamos finalmente la corriente.
I=\frac{\left(3623550 J\right)}{\left(200 v\right)\left(3000 s\right)}=6.04 A
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 9: Fuerza magnética sobre una Corriente
Una corriente de 2 A circula por un conductor de 20 cm de longitud que se encuentra en un campo magnético de 500 mT . Determina la fuerza sobre el conductor considerando que este se coloca perpendicular al campo.
- 0.2 N
- 0.3 N
- 0.1 N
- 0.4 N
Solución:
Si un conductor con corriente se introduce de manera perpendicular en un campo magnético, sobre las cargas en movimiento actuarán fuerzas magnéticas que originarán una fuerza neta sobre el conductor. La magnitud de dicha fuerza puede calcularse como:
F=iLB
Donde i es la intensidad de la corriente, L la longitud del conductor y B la intensidad del campo magnético. En este caso:
i=2 A, L=0.2 m, B=500\times {10}^{-3} T
Sustituimos.
F=\left(2 A\right)\left(0.2 m\right)\left(500\times {10}^{-3} T\right)=0.2 N
La respuesta correcta es el inciso a).
Reactivo 10: Refracción de la Luz
Un haz de luz pasa del vidrio, con índice de refracción igual a 1.66, al agua, la cual tiene un índice de refracción de 1.33. El ángulo de incidencia es de 40°. ¿Cuál es el seno del ángulo de refracción? ¿Cuál es el valor del ángulo de refracción?
- 0.3211,{25.22}^{\circ }
- 0.2522,{32.11}^{\circ }
- 0.5335,{80.23}^{\circ }
- 0.8023,{53.35}^{\circ }
Solución:
La luz, al pasar de un medio a otro, cambia la dirección de propagación en el segundo medio. A este fenómeno se le conoce como refracción de la luz y se debe al cambio de velocidad que presenta la luz según el medio en el que se propaga.
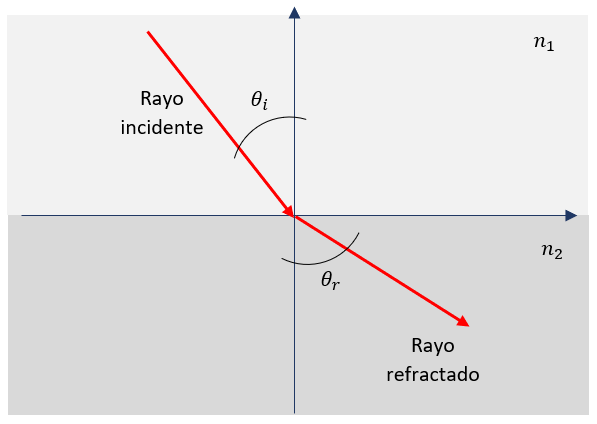
La ley de Snell establece que el cociente entre los senos de los ángulos de incidencia y refracción es inversamente proporcional al cociente de sus índices de refracción.
\frac{sin {\theta }_{i} }{sin {\theta }_{r} }=\frac{{n}_{2}}{{n}_{1}}
Despejamos el seno del ángulo de refracción. En este caso, el vidrio es el primer medio y el agua el segundo.
sin {\theta }_{r} =sin {\theta }_{i} \frac{{n}_{1}}{{n}_{2}}=sin 40° \frac{1.66}{1.33}=0.8023
Aplicamos identidad inversa para obtener el valor del ángulo.
sin {\theta }_{r} =0.8023\to {\theta }_{r}={\mathrm{sin}}^{-1}\left(0.8023\right)
{\theta }_{r}=53.35°
Finalmente:
0.8023, 53.35°
Concluimos que la respuesta correcta es la opción d).

