En esta entrada vamos a resolver los reactivos de estadística que aparecen en la guía UANL 2021 para la prueba de ingreso. Puedes consultar las soluciones paso a paso de los ejercicios, con trucos que te ayudarán a mejorar el rendimiento durante el examen.

La guía de estudios diseñada por la Pearson es extensa y en ella se explica todo sobre el proceso de admisión. A continuación, puedes ver un resumen de la convocatoria UANL 2021.
- Períodos de ingreso: Dos al año.
- Inicio de registro: Abril y Octubre
- Carreras ofertadas: 100+
- Examen de admisión: Pearson
- Porcentaje de Aceptación: 50%
Estructura del examen de la UANL
La prueba esta conformada por dos partes:
- Conocimientos Generales, con un total de 4 módulos
- Conocimientos por Área, relacionados con la carrera que el aspirante desea estudiar
Los conocimientos por área cambiarán según la facultad a la que pertenezca tu carrera. Consulta la lista de carreras ofertadas haciendo click en el siguiente enlace.
Tabla de contenido del examen de admisión.
| Partes del examen | Áreas | Reactivos | Tiempo |
|---|---|---|---|
| Primera | Pensamiento matemático y analítico | 50 | 90 |
| Estructura de la lengua y comprensión lectora | 50 | 90 | |
| Segunda | Inglés | 20 | 20 |
| Comprensión lectora | 20 | 30 | |
| Área de conocimiento 1 | 20 | 20 | |
| Área de conocimiento 2 | 20 | 20 | |
| Totales | 180 | 270 |
Temario del Área de Estadística
Revisa los temas de estadística que debes estudiar en esta sección. La estadística suele ser extensa y confusa, por lo tanto, comprende y analiza los conceptos detalladamente antes de realizar los problemas.
Estadística descriptiva
- Noción y utilidad de la estadística descriptiva
- Definición de población y muestra
- Variables aleatorias
- Distribucion de frecuencias
- Medidas de tendencia central
- Medidas de dispersión
- Representaciones gráficas de datos
Teoría de conjuntos
- Características de la teoría de conjuntos
- Operaciones de conjuntos
- Diagramas de Venn-Euler
Probabilidad
- Concepto y aplicación de probabilidad
- Noción de la estadística inferencial
- Espacio muestral: diagramas de árbol, combinaciones y técnicas de conteo
- Experimentos aleatorios y determinísticos
- Distribuciones de probabilidad: binomial, normal y teorema de Bayes
- Enfoques de la probabilidad: subjetivo, frecuencial y clásico
Guía UANL de Estadística resuelta
Ahora sigue la solución de los 8 reactivos. Te invito a continuar estudiando y practicando, ya que la guía no cubre todo el temario de estadística del examen.
Reactivo 1: Medidas de Dispersión
Los siguientes valores corresponden a las posiciones en las que ha quedado un corredor amateur en un maratón.
89\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}91\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}55\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}7\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}20\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}99\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}25\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}81\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}19\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}82\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}60
Determina el rango, desviación estándar y varianza del conjunto de datos.
- Rango 99,{s}^{2}=1149.5,s=33.9
- Rango 92,{s}^{2}=1149.5,s=33.9
- Rango 32,{s}^{2}=1009.5,s=3.39
- Rango 33.9,{s}^{2}=1149.5,s=92
Solución:
Antes de proceder al cálculo de las medidas de dispersión solicitadas, procedemos a ordenar de forma creciente el conjunto de datos.
7, 19, 20, 25, 55, 60, 81, 82, 89, 91, 99
Comencemos por calcular el rango o amplitud. Corresponde al recorrido de una distribución y se define como la resta entre el valor mayor con el menor; en este caso 99 y 7.
R=99-7=92
Se llama varianza, representada por {s}^{2} , a la media aritmética de los cuadrados de las desviaciones, para el conjunto de datos dado. Por lo tanto, debemos calcular la media del conjunto, restar cada dato con la media, sumar todo y luego dividir entre el número total de datos menos uno, es decir, n-1=11-1=10 .
Cálculo de la media aritmética.
\stackrel{-}{x}=\frac{7+19+20+25+55+60+81+82+89+91+99}{11}=57.09
Aproximamos el valor a 57 porque nos referimos a posiciones.
\stackrel{-}{x}=57
Restamos cada dato con la media.
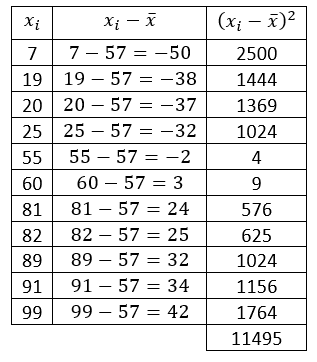
Calculamos la varianza como:
{s}^{2}=\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{n-1}=\frac{11495}{10}=1149.5
La desviación estándar, denotada como s , se calcula como la raíz cuadrada de la varianza.
s=\sqrt{s}=\sqrt{1149.5}=33.9
Finalmente:
R=92,{s}^{2}=1149.5,s=33.9
Comparando con las opciones, la respuesta correcta está en el inciso b).
Reactivo 2: Medidas de tendencia Central
Para los siguientes datos determina la media, mediana y moda.
3600\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}1700\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}4000\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}3900\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}3100\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}3800\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}2200\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}3000
- \stackrel{-}{x}=3162.5,\stackrel{~}{x}=3100,\widehat{x}= No existe
- \stackrel{-}{x}=2162.5,\stackrel{~}{x}=3350,\widehat{x}= No existe
- \stackrel{-}{x}=3162.5,\stackrel{~}{x}=3350,\widehat{x}= No existe
- \stackrel{-}{x}=3162.5,\stackrel{~}{x}=3600,\widehat{x}= No existe
Solución:
Los parámetros de centralización o medidas de tendencia central, son llamados de esta manera porque son valores que, por sus características, tienden a situarse en torno a un valor hacia el centro del conjunto de datos ordenados.
Teniendo en cuenta lo anterior, antes de proceder a los cálculos, debemos ordenar los datos ofrecidos por el enunciado en forma creciente.
1700, 2200, 3000, 3100, 3600, 3800, 3900, 4000
La media, llamada también promedio, es el cociente entre la suma de todos los valores y el número n de todos los datos.
\stackrel{-}{x}=\frac{\sum {x}_{i}}{n}
Sustituimos y calculamos.
\stackrel{-}{x}=\frac{1700+2200+3000+3100+3600+3800+3900+4000}{8}=3162.5
\therefore \stackrel{-}{x}=3162.5
La moda de una variable estadística es el valor que presenta mayor frecuencia, es decir, el valor que más se repite. En este caso, no existe ningún dato que se repita más que otros, por tanto, el conjunto no posee moda.
\widehat{x}= No existe
La mediana es el valor central del conjunto de datos, una vez ordenados de menor a mayor. La mediana divide a los datos en dos partes iguales. El cálculo de la mediana para datos desagrupados depende de si el total de valores es par o impar.
- Si el número de datos es par, se toma el valor promedio de los datos centrales
- Si el número de datos es impar, se toma el valor central
Ya que n=8 , el conjunto es par y, por tanto, debemos calcular la media de los datos centrales, los cuales son: 3100 y 3600 .
\stackrel{~}{x}=\frac{3100+3600}{2}=3350
\therefore \stackrel{~}{x}=3350
Finalmente:
\stackrel{-}{x}=3162.5,\stackrel{~}{x}=3350,\widehat{x}= No existe
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 3: Parámetros estadísticos para datos agrupados
Para los siguientes datos, determina la media, mediana, moda y desviación estándar.
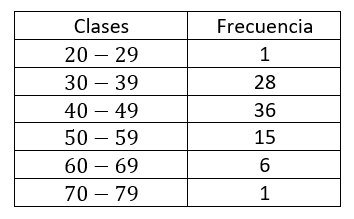
- \stackrel{-}{x}=42.76,\stackrel{~}{x}=44.03,\widehat{x}=45,s=8.54
- \stackrel{-}{x}=44.03,\stackrel{~}{x}=45,\widehat{x}=42.76,s=7.54
- \stackrel{-}{x}=42.76,\stackrel{~}{x}=44.03,\widehat{x}=45,s=5.54
- \stackrel{-}{x}=44.5,\stackrel{~}{x}=43.63,\widehat{x}=42.48,s=9.59
Solución:
En este caso, el conjunto de datos se encuentra agrupado por intervalos, llamados también intervalos de clase. El cálculo de los parámetros estadísticos básicos cambia ligeramente, ya que introducimos el concepto de marca de clase como el valor representativo de cada intervalo a la hora de realizar los cálculos.
La media aritmética para datos agrupados se obtiene multiplicando cada marca de clase por su frecuencia y la suma de todos estos productos es dividida entre el número de observaciones.
\stackrel{-}{x}=\frac{\sum {m}_{i}\bullet {f}_{i}}{n}
Donde {m}_{i} es la marca de cada clase que se obtiene:
{m}_{i}=\frac{L{S}_{i}+L{I}_{i}}{2}
Donde L{S}_{i} y L{I}_{i} son los límites inferior y superior de la clase.
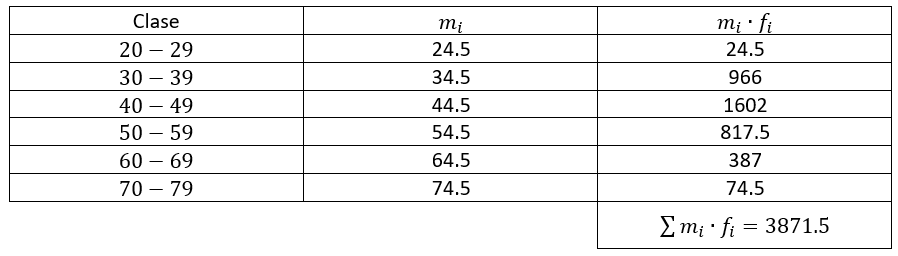
\stackrel{-}{x}=\frac{\sum {m}_{i}\bullet {f}_{i}}{n}=\frac{3871.5}{87}=44.5
Para calcular la mediana de un conjunto de datos agrupados, debemos emplear la siguiente ecuación \stackrel{~}{x}={L}_{i}+\frac{\frac{N}{2}-{F}_{i-1}}{{f}_{i}}\cdot {a}_{i} y, además, es necesario calcular las frecuencias acumuladas de cada clase. A continuación, empleamos una tabla para las frecuencias acumuladas.
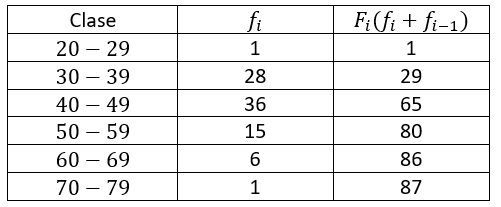
Ahora, dividimos la frecuencia acumulada total entre dos, porque nos interesa localizar el intervalo que contiene la mediana.
\frac{87}{2}=43.5
El intervalo con frecuencia acumulada inmediatamente mayor a 43.5 es 40-49 . Con esto, aplicamos la fórmula de la mediana:
\stackrel{~}{x}={L}_{i}+\frac{\frac{N}{2}-{F}_{i-1}}{{f}_{i}}\cdot {a}_{i}
{L}_{i}=40;\frac{N}{2}=43.5;{F}_{i-1}=29;{f}_{i}=36;{a}_{i}=49-40=9
Sustituimos.
\stackrel{~}{x}=40+\frac{43.5-29}{36}\cdot 9=43.63
La moda en un conjunto de datos agrupados, se busca en el intervalo con la frecuencia absoluta {f}_{i} mayor y se calcula con la siguiente ecuación \widehat{x}={L}_{i}+\frac{{f}_{i}-{f}_{i-1}}{\left({f}_{i}-{f}_{i-1}\right)+\left({f}_{i}-{f}_{i+1}\right)}\bullet {a}_{i} . En nuestro caso, el intervalo con la {f}_{i} mayor es 40-49 ; entonces:
{f}_{i}=36; {f}_{i-1}=28; {f}_{i+1}=15; {L}_{i}=40
Sustituimos en la ecuación.
\widehat{x}=40+\frac{36-28}{\left(36-28\right)+\left(36-15\right)}\bullet 9=42.48
La desviación típica o estándar para datos agrupados se calcula empleando la siguiente ecuación.
s=\sqrt{\frac{\sum ({x}_{i}-\underset{\_}{x}{)}^{2}\cdot {f}_{i}}{N}}
Donde los {x}_{i} son las marcas de clase y N es el total de datos. Organizamos los datos de interés en la siguiente tabla, recordando que \stackrel{-}{x}=44.5 .
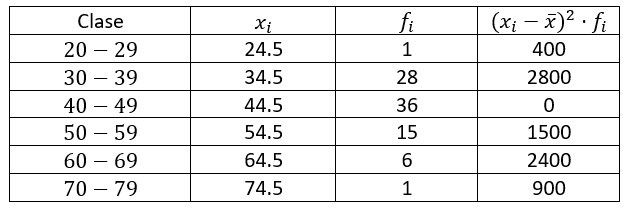
Finalmente:
s=\sqrt{\frac{400+2800+0+1500+2400+900}{87}}=9.59
Concluimos entonces:
\stackrel{-}{x}=45,\stackrel{~}{x}=43.63,\widehat{x}=42.48,s=9.59
Escogemos como correcta la opción d).
Reactivo 4: Problema de aplicación
En la siguiente tabla se muestra la estadística de anotaciones de los 30 mejores anotadores de la historia del fútbol soccer. Obtén las medidas de tendencia central de la distribución.
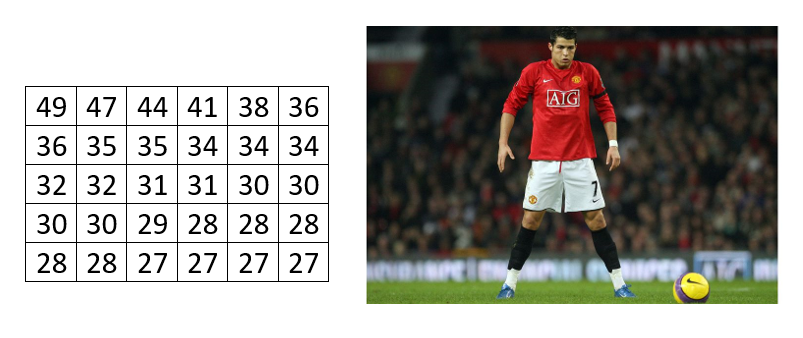
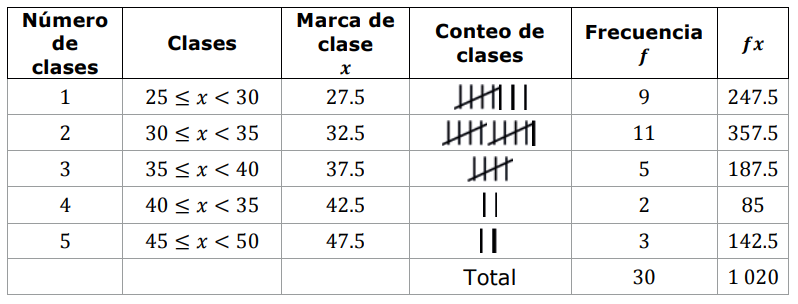
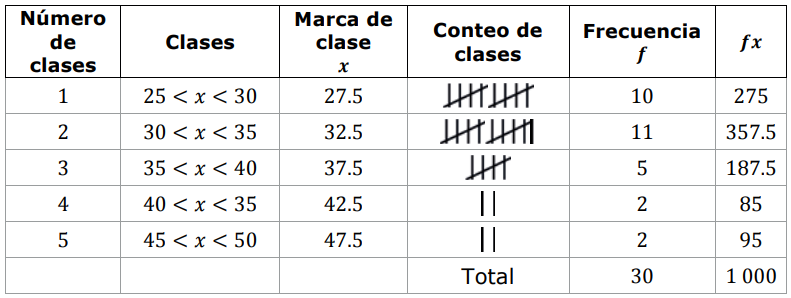
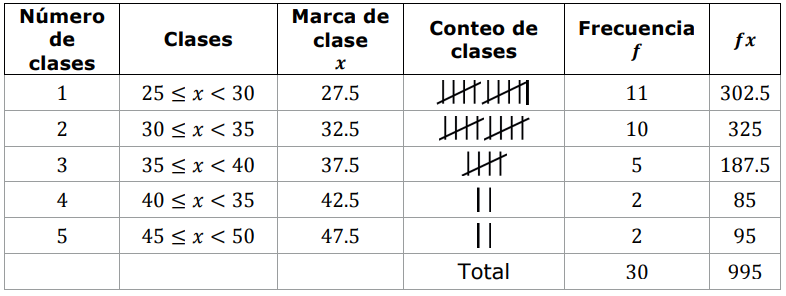
- Con la información proporcionada indica cuál de las siguientes tablas representa mejor a los datos
- ¿Cuál es la media?
- 33.\underset{\_}{3}
- 33.\underset{\_}{16}
- 34
- 33
- ¿Cuál es la mediana?
- 33
- 34
- 32.\underset{\_}{27}
- 33.\underset{\_}{1}
- ¿Cuál es la moda?
- 31.714
- 30.714
- 29.714
- 32.714
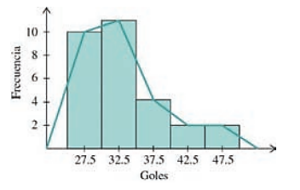
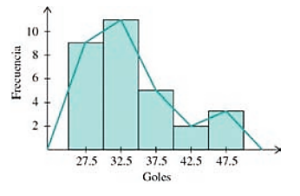
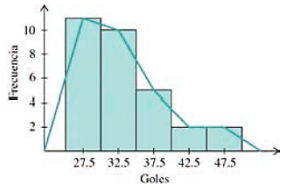
- Selecciona la gráfica que corresponde al histograma y el polígono de frecuencias de los datos analizados
Solución:
A lo largo de los incisos que tiene el problema, se nos da una pista del procedimiento que debemos seguir para calcular correctamente los parámetros de tendencia central que solicita. Lo primero, es ordenar los datos en una tabla de distribución de frecuencias, iniciemos por ordenar todo de forma creciente.
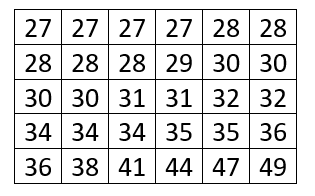
- Debido a la gran cantidad de datos (unos 30 valores), será útil agruparlos por intervalos. Comencemos por calcular el rango del conjunto de datos.
R=49-27=22
- Ahora, calculamos el número de intervalos con el método de Sturges.
{n}_{int}=1+\mathrm{3,322}\cdot logN
Sustituimos N=30 .
{n}_{int}=1+\mathrm{3,322}\cdot loglog 30 =5.9\approx 5
Se aproxima al número menor. El número de intervalos es 5.
- Calculamos la amplitud de los intervalos dividiendo el rango entre el número de intervalos.
I=\frac{R}{{n}_{int}}=\frac{22}{5}=4.4\approx 5
Redondeamos al inmediato superior. Debido al redondeo, se ha alterado el valor del rango y debe ser recalculado.
{R}^{\text{'}}=I{n}_{int}=\left(5\right)\left(5\right)=25
El nuevo rango es de 25.
- Formamos los intervalos, tomando como punto inicial el valor más bajo del conjunto de datos, para sumarle la amplitud de los intervalos hasta llegar al rango R\text{'} . El excedente del rango lo repartimos entre los extremos superior e inferior: 25 para el inferior (hemos restado 2) y 50 para el superior (hemos sumado 1)
Se sigue cumpliendo el rango R\text{'} :
{R}^{\text{'}}=50-25=25

- Agregamos a la tabla una columna con la frecuencia de cada intervalo, es decir, contamos cuántas veces aparecen los números de dicho intervalo en la tabla de datos inicial
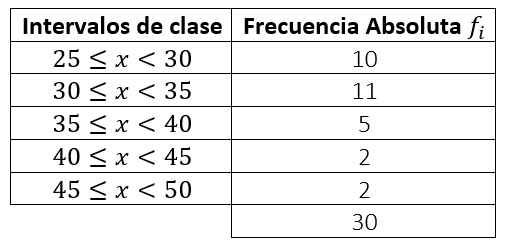
- Finalmente, agregamos una columna con la marca de cada clase y el producto {x}_{i}{f}_{i} que será útil a la hora de realizar cálculos posteriores
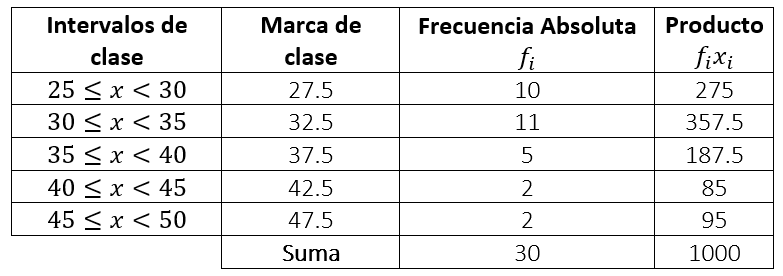
Hasta este punto, podemos indicar una respuesta para el inciso a). Tanto la opción ii. como la iii. Son válidas pero ambas tienen el mismo error: el intervalo 4 tiene el extremo superior incorrecto.
Siguiendo la lógica de la respuesta correcta según la guía, asumiremos que fue un error de tipografía en la opción iii. Y la indicamos como nuestra respuesta correcta para el inciso a).
Cálculo de la media.
Para calcular la media aritmética de un conjunto de datos agrupados, debemos emplear la siguiente ecuación:
\stackrel{-}{x}=\frac{\sum {x}_{i}{f}_{i}}{\sum {f}_{i}}
Ambos valores se encuentran en la tabla, por tanto, solo queda sustituir.
\stackrel{-}{x}=\frac{1000}{30}=33.\underset{\_}{3}
Comparando con las opciones para el inciso b), seleccionamos como correcta la opción i.
Cálculo de la mediana.
La mediana para datos agrupados se calcula con la siguiente ecuación:
\stackrel{~}{x}={L}_{i}+\frac{\frac{N}{2}-{F}_{i-1}}{{f}_{i}}\cdot {a}_{i}
El intervalo se selecciona realizando la división \frac{N}{2} , el que tenga una frecuencia acumulada inmediatamente superior, será el intervalo de la mediana. Debemos agregar una columna con la frecuencia acumulada de cada intervalo.
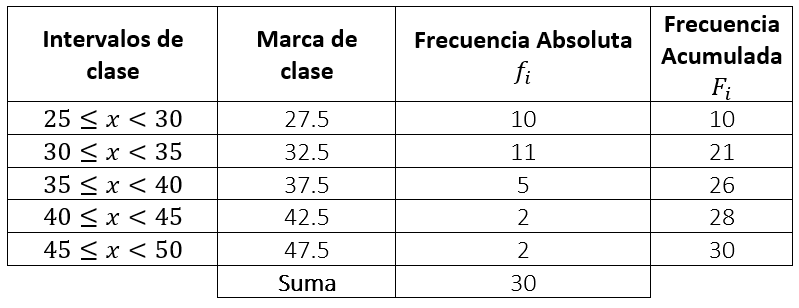
\frac{N}{2}=\frac{30}{2}=15
El intervalo de la mediana es 30\le x<35 . De esta manera:
{L}_{i}=30; \frac{N}{2}=15;{F}_{i-1}=10;{f}_{i}=11;{a}_{i}=5
Sustituimos.
\stackrel{~}{x}=30+\frac{15-10}{11}\cdot 5=32.\underset{\_}{27}
Comparando con las opciones del inciso c), la respuesta correcta es la iii.
Cálculo de la moda.
Para calcular la moda en un conjunto de datos agrupados, determinamos la clase con la mayor frecuencia y luego aplicamos esta ecuación:
\widehat{x}={L}_{i}+\frac{{f}_{i}-{f}_{i-1}}{\left({f}_{i}-{f}_{i-1}\right)+\left({f}_{i}-{f}_{i+1}\right)}\bullet {a}_{i}
En nuestro caso, el intervalo con frecuencia absoluta mayor es 30\le x<35 . Entonces:
{L}_{i}=30;{f}_{i}=11, {f}_{i-1}=10;{f}_{i+1}=5;{a}_{i}=5
Sustituimos.
\widehat{x}=30+\frac{11-10}{\left(11-10\right)+\left(11-5\right)}\bullet 5=30.714
Observando las opciones del inciso d), la respuesta correcta es la ii.
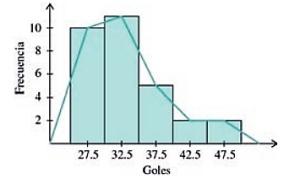
Histograma y polígono de frecuencias.
En este caso, podemos hacer la gráfica a mano empleando una hoja milimétrica o en un software similar a Microsoft Excel. Por obvias razones, emplearemos Excel en este caso. La gráfica quedaría de la siguiente forma:
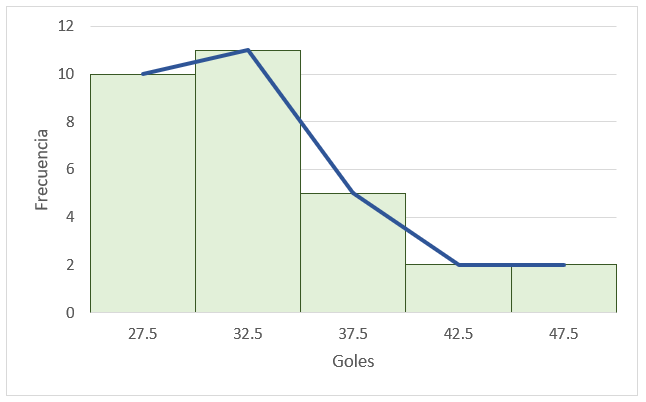
Comparando con las opciones del inciso e), los candidatos parecen ser ii y iv, pero ii tiene mal la frecuencia del intervalo 3, mientras que iv está totalmente correcto. Concluimos entonces que la respuesta correcta es iv.
Uniendo todas las respuestas nos queda:
a) iii, b) i, c) iii, d) ii, e) iv
Reactivo 5: Gráficos de barras
¿Cuáles de las siguientes opciones son los tipos de gráficas de barras?
- Verticales, horizontales, histograma, bidireccional, ojivas, etc
- Verticales, circulares, histograma, bidireccional, pirámide de población, etcétera
- Verticales, horizontales, histograma, bidireccional, pirámide de población, etcétera
- Verticales, horizontales, histograma, bidireccional, seccionada, etc
Solución:
Los gráficos de barras, son un tipo de gráfico ampliamente utilizado en estadística y probabilidad para la representación de variables discretas y agrupadas.
Se componen de dos o tres ejes y la magnitud de la variable es representada por alguna de las aristas del rectángulo; alto, ancho o profundidad, según el tipo de gráfico.
Las barras pueden ser sencillas, acomodadas de forma horizontal o vertical o representar la frecuencia de una variable, empleado en histogramas. Los gráficos bidireccionales o de pirámide de población, se emplean para contrastar las características de dos sujetos expuestos al mismo experimento.
Además de estas, existen otras grafica de barras especiales como:
- Apiladas
- Agrupadas
- De promedios
- Barras de rangos
Concluimos que la respuesta correcta es la opción c).
Reactivo 6: Histograma de frecuencia
¿Para qué se utiliza el histograma?
- Se usa para representar las frecuencias de una variable cuantitativa continua
- Se usa para representar las frecuencias porcentuales acumuladas ascendentes de una variable cuantitativa
- Se usa para representar las frecuencias absolutas de una variable cuantitativa
- El histograma no corresponde a un gráfico de barras
Solución:
Los histogramas de frecuencia son un tipo de gráfico de barra donde la altura o anchura de la barra representa la frecuencia de ocurrencia para determinado evento o subconjunto de eventos.
Se emplean generalmente como representación gráfica de la tendencia que tiene una determinada característica continua y cuantitativa, de ocurrir. En base a este análisis, podemos concluir que la respuesta correcta es el inciso a).
Se usa para representar las frecuencias de una variable cuantitativa continua.
Reactivo 7: Uso de las gráficas de barras
¿Para qué se utilizan las gráficas de barras?
- Se utilizan para poder apreciar con claridad los valores de la variable analizada y poder trazar el polígono de frecuencia
- Se utilizan en general para comparar magnitudes de varias categorías o la evolución de una magnitud concreta
- Se utiliza para comparar diferentes magnitudes analizadas representando los datos de diversas formas
- Las gráficas de barras se utilizan para poder representar de forma pictórica los valores de las frecuencias acumuladas
Solución:
Debido a que las gráficas de barras muestran el tamaño de las clases, es intuitivo realizar con ellas la comparación de los valores o magnitudes de estas categorías. Concluimos indicando como correcta la opción b).
Reactivo 8: Gráfico de barras e histograma
Menciona las diferencias que existen entre las gráficas de barras y el histograma.
- Las gráficas de barras se trazan con una separación entre las barras y el histograma no presenta ningún tipo de separación
- Los histogramas de barras se trazan con una separación entre las barras y las gráficas de barras no presentan ningún tipo de separación
- La altura de las gráficas de barras son mayores en comparación con las barras de los histogramas
- No existen diferencias entre las gráficas de barras y el histograma
Solución:
En general, los gráficos de barra son una forma para la representación de datos que puede o no ser más útil para determinados conjuntos de información.
Por otro lado, los histogramas representan de forma gráfica la tendencia que tiene una variable en determinados subgrupos de datos y una de las formas de representar un histograma es mediante un gráfico de barras verticales.
La diferencia crucial entre ambos, es que las barras en un histograma se dibujan unas pegadas con otras, mientras que los gráficos de barras convencionales suelen tener separación para mayor claridad.
Tomando en cuenta nuestro análisis, la respuesta correcta es la opción a).