¡Hola de nuevo aspirante! En este post vamos a resolver la primera parte de la guía de Razonamiento Matemático UAM para la división de Ciencias Biológicas y de la Salud (CBS) que consta de 12 reactivos, desde el 26 al 37.

Como advertimos en todas nuestras guías, resuelve primero los reactivos por tu cuenta. Utiliza este material como consulta o para salir de dudas.
El siguiente es un resumen de la convocatoria UAM que contiene la información más resaltante.
- Número de convocatorias: Dos al año.
- Fechas de registro: marzo y agosto del 2022
- Oferta académica: 82 carreras
- Divisiones académicas: 6
- Modalidad: en línea
Estructura del examen de ingreso UAM 2022
La prueba de ingreso se divide en dos partes:
- Prueba de aptitud
- Prueba de conocimientos específicos
La prueba de aptitud tiene preguntas sobre Razonamiento Matemático y Razonamiento Verbal, con un total de 40 reactivos repartidos en partes iguales.
La segunda parte depende de la división a la que pertenezca tu carrera. En el caso de Ciencias Biológicas y de la Salud, las preguntas están divididas entre: química, biología y física.
A continuación, tienes un resumen de los subtemas en cada una de las asignaturas de la segunda parte del examen.
Biología
- Evolución
- Bioquímica
- Citología
- Genética
- Histología
- Anatomía y fisiología
- Diversidad de organismos
- Ecología
- Educación para la salud
Física
- Estándares de medición
- Cinemática
- Dinámica
- Termodinámica
- Electromagnetismo
- Óptica
Química
- Química general
- Química inorgánica
- Química orgánica
Resumen de reactivos en cada parte del examen.
| Área | Reactivos | Porcentaje |
|---|---|---|
| Razonamiento verbal | 20 | 25% |
| Razonamiento matemático | 20 | 25% |
| Conocimientos específicos | 40 | 50% |
| Total | 80 | 100% |
Temario de Razonamiento Matemático para CBS
La prueba de Razonamiento Matemático no solo está compuesta por series y sucesiones, también hay problemas de modelado matemático y la aplicación de temas diversos sobre matemáticas. El siguiente, es un desglose detallado de dicha parte.
Razonamiento numérico
- Realizar estimaciones numéricas y cálculos diversos
- Solucionar problemas
- Llevar a cabo demostraciones, pruebas y conclusiones
- Efectuar manipulaciones matemáticas
- Reconocer variables o factores- reconocimiento de igualdades
- Mecanizaciones
- Completar sucesiones numéricas
- Completar series lógicas
- Analogía simbólica y transferencia de códigos
- Interpretación de símbolos
- Inferencia de tendencias
- Interpolar y extrapolar; y escoger, interpretar y construir medios de representación-variantes gráficas, mapas y tablas.
Guía UAM Razonamiento Matemático Parte 1
Luego de esta introducción, en la que hemos repasado el temario de Razonamiento Matemático y otros aspectos relevantes para el examen, vamos con la solución paso a paso de los primeros 12 reactivos de la guía para la división de Ciencias Biológicas y de la Salud.
Reactivo 26: Sucesiones numéricas
En las sucesión numérica 8, 7, 11, 10, 14,…, los dos números siguientes son:
- 13, 16
- 18, 14
- 13, 17
- 18, 17
- 15, 18
Solución:
Para encontrar los números faltantes de la sucesión, debemos identificar la regla con la que cambian.
La sucesión inicia en 8 y luego disminuye 1 por tanto, el segundo término es 7. El tercer término incrementa en 4 unidades respecto al segundo, pasa de 7 a 11 y el cuarto vuelve a disminuir en 1, quedando ahora en 10.
El quinto término incrementa nuevamente en 4 unidades, pasa de 10 a 14. Esto ya nos da una clara idea de la regla que sigue la sucesión.
Decrece 1, incrementa 4, decrece 1, incrementa 4,…
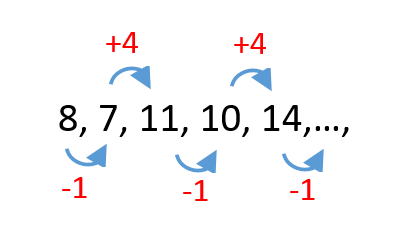
De esta forma, el sexto elemento debe disminuir en 1, es decir 13 y el séptimo debe incrementar en 4, es decir 17.
8, 7, 11, 10, 14, 13, 17,…
Comparando con las opciones, la respuesta correcta es la opción C.
Reactivo 27: Sucesiones numéricas
En la sucesión numérica 75, 74, 72, 71,… los dos números siguientes son:
- 69, 71
- 69, 67
- 68, 67
- 69, 68
- 15, 18
Solución:
Procedemos a identificar la regla que hace cambiar a los números de la sucesión. El primer término es 75, que disminuye 1 para que el segundo sea 74.
El tercer término es 72, por lo que disminuyó dos unidades para pasar del segundo al tercero. El cuarto término vuelve a disminuir en uno y se coloca en 71. La regla en esta sucesión es:
Disminuye 1, disminuye 2, disminuye 1, disminuye 2,…
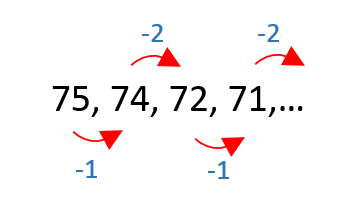
En base a esto, el quinto término debe disminuir dos respecto al cuarto, es decir 69 y el sexto 1 respecto al quinto, 68.
75, 74, 72, 71, 69, 68,…
Comparando con las opciones, concluimos seleccionando a la D como la respuesta correcta.
Reactivo 28: Sucesiones numéricas
En la sucesión numérica 6, 18, __, 360, 2160, el número que falta es:
- 48
- 72
- 54
- 36
- 90
Solución:
En esta sucesión, el incremento entre términos es brusco. Eso nos indica que la regla de cambio entre términos sucesivos es un producto o una potencia.
La sucesión inicia en 6, el segundo término es 18 que se obtiene al multiplicar por 3 al primero:
{a}_{2}=3*{a}_{1}=3*6=18
El tercer término es desconocido. El quinto término puede obtenerse al multiplicar el cuarto término por 6:
{a}_{5}=6*{a}_{4}=6*360=2160
Esto por ahora no dice mucho, pero podemos descomponer al primer término como:
{a}_{1}=2*3=6
Escribamos cada término uno debajo del otro.
{a}_{1}=2*3=6
{a}_{2}=3*{a}_{1}=18
{a}_{3}=?
{a}_{4}=360
{a}_{5}=6*360
Si observamos con detenimiento, el primero es 2 por 3, el segundo 3 por el primero,… el quinto 6 por el cuarto. Es decir, el siguiente elemento se consigue al multiplicar el anterior por la posición del siguiente más 1.
{a}_{n}=\left(n+1\right){a}_{n-1}
De esta forma, el tercer elemento debería ser 4 multiplicado por el segundo:
{a}_{3}=4*{a}_{2}=4*18=72
Esto lo podemos rectificar, si obtenemos al cuarto elemento como el tercero multiplicado por 5:
{a}_{4}=5*{a}_{3}=5*72=360
En efecto, esta es la regla de la sucesión. Completando nos queda:
6, 18, 72, 360, 2160,…
Comparando con las opciones, seleccionamos como correcta a la B.
Reactivo 29: Sucesiones numéricas
En la sucesión 2, 3, 5, 8,…, el número siguiente es:
- 10
- 11
- 13
- 14
- 16
Solución:
Debido a que los cambios no son bruscos entre un término y otro, la regla de incremento debe ser una suma.
El segundo elemento se obtiene al sumar 1 al primero 3=2+1 , el tercero de sumar 2 al segundo 5=3+2 , el cuarto de sumar 3 al tercero 8=5+3 , por tanto el quinto término debe ser igual a sumar 4 al cuarto:
{a}_{5}=8+4=12
Pero esta respuesta no se encuentra en los incisos. Si examinamos ahora los números que se van sumando:
1, 2, 3,\dots
Corresponden a los 3 primeros números primos, por tanto el siguiente primo no es 4 sino 5. De esta forma, la regla es sumar consecutivamente un número primo al anterior para obtener el siguiente término de la sucesión.
El número siguiente es:
{a}_{5}=8+5=13
2, 3, 5, 8, 13,…
Finalmente, indicamos como respuesta correcta a la opción C.
Reactivo 30: Sucesiones numéricas
En la sucesión numérica 9, 17, 11, 19,…, el número siguiente es:
- 11
- 13
- 15
- 22
- 27
Solución:
Para determinar la regla que rige a la sucesión, debemos examinar en qué cantidades varían unos términos respecto de otros.
La sucesión inicia en 9, el segundo término se obtiene sumando 8 al primero 9+8=17 , el tercero restando 6 al segundo 17-6=11 y el cuarto sumando 8 al tercero 11+8=19 .
Con este rápido análisis es evidente que la regla de la sucesión es:
Sumar 8, restar 6, sumar 8, restar 6,…
Por tanto, el quinto término se obtiene restando 6 al cuarto término:
{a}_{5}=19-6=13
La serie quedaría como:
9, 17, 11, 19, 13,…
La respuesta correcta es la B.
Reactivo 31: Sucesiones numéricas
En la sucesión numérica 13, 18, 24, 29,…, los dos números que siguen son:
- 34, 39
- 34, 41
- 35, 40
- 35, 39
- 35, 41
Solución:
Identificamos la regla que rige a la sucesión analizando cuánto crece un término respecto de otro.
La sucesión inicia en 13; el segundo término es 5 unidades mayor al primero 13+5=18 , el tercero es 6 unidades mayor al segundo 18+6=24 y el cuarto término 5 unidades mayor que el tercero 24+5=29 .
En base al análisis anterior, determinamos que la regla es:
Sumar 5, sumar 6, sumar 5,…
Por tanto, si en el cuarto término se sumaron 5 para el quinto toca sumar 6:
{a}_{5}=29+6=35
Para el sexto toca sumar 5:
{a}_{6}=35+5=40
La sucesión con dos términos más queda como:
13, 18, 24, 29, 35, 40,…
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 32: Fracciones y proporciones
Una botella tiene una capacidad total de \frac{9}{5} litros y contiene aceite en \frac{5}{9} de su capacidad ¿Cuánto aceite, en litros, hay en la botella?
- 0.555
- 1
- \frac{56}{45}
- \frac{25}{81}
- \frac{81}{25}
Solución:
Para calcular los litros de aceite que tiene la botella, debemos hacer el producto de la fracción en la que se encuentra llena la botella, es decir \frac{5}{9} por la capacidad en litros de la botella, en este caso \frac{9}{5} litros.
Litros de aceite=\frac{9}{5}l*\frac{5}{9}=1 litro
Cuando la botella está a \frac{5}{9} de su capacidad total, alberga 1 litro de aceite. Comparando con las opciones, seleccionamos como correcta a la opción B.
Reactivo 33: Problemas con fracciones
En un grupo de 60 alumnos, cierto día \frac{1}{10} del grupo es atacado por una infección; \frac{2}{3} de los infectados deciden permanecer en cama, mientras que el resto de todo el grupo asiste a clase. El número de alumnos que asistieron a clase es:
- 6
- 40
- 54
- 56
- 58
Solución:
En base a lo que nos dice el enunciado, de los estudiantes infectados \frac{2}{3} decide quedarse en casa, por tanto \frac{1}{3} asiste a clases junto al grupo que no ha sido infectado.
El número total de estudiantes que asistieron se calcula como la suma de la fracción de infectados que decidió asistir más el resto de estudiantes que no fueron infectados:
Estudiantes que asistieron=Infectados que asistieron+No infectados
Los no infectados es el restante a \frac{1}{10} , es decir \frac{9}{10} :
No infectados=60*\frac{9}{10}=54
Ahora, calculamos el total de infectados y a ese resultado lo multiplicamos por la fracción de infectados que asistieron, es decir \frac{1}{3} .
Infectados=60*\frac{1}{10}=6
Infectados que asistieron=6*\frac{1}{3}=2
Sustituimos:
Estudiantes que asistieron=2+54=56
El número de alumnos que asistieron a clase es: 56
Comparando con las opciones, seleccionamos como correcta a la D.
Reactivo 34: Término general de la sucesión
La lista de números 1, 6, -1 se obtiene al sustituir respectivamente n=1, 2, 3 en la expresión:
- 3(-1{)}^{n-1}+n
- 2(-1{)}^{n}+4-n
- (-1{)}^{n}+2n
- (-1{)}^{2n}+1
- 3(-1{)}^{n}+5-n
Solución:
Para resolver este problema tenemos dos opciones:
- Estudiar cómo cambian los números en la lista y calcular la expresión
- Sustituir los valores de n en cada una y corroborar si cumple o no
Por ser la opción más rápida y menos tediosa, recurriremos a sustituir los valores de n en cada una hasta dar con la correcta. La lista es solo de 3 números, así que será fácil de comprobar.
En adición, si tienes buen dominio de tu calculadora puedes utilizar la función EVALUAR o TABLA (varía según el modelo) para acelerar aún más los cálculos.
Expresión del inciso A.
n=1\to 3(-1{)}^{1-1}+1=3\left(1\right)+1=4
El primer término no cumple, no es la expresión correcta.
Expresión del inciso B.
n=1\to 2(-1{)}^{n}+4-n=2\left(-1\right)+4-1=1
n=2\to 2(-1{)}^{n}+4-n=2{\left(-1\right)}^{2}+4-2=4
El segundo término no cumple, no es la expresión correcta.
Expresión del inciso C.
n=1\to (-1{)}^{n}+2n={\left(-1\right)}^{1}+2\left(1\right)=1
n=2\to (-1{)}^{n}+2n={\left(-1\right)}^{2}+2\left(2\right)=5
El segundo término no cumple, no es la expresión correcta.
Expresión del inciso D.
n=1\to (-1{)}^{2n}+1=2
El primer término no cumple, no es la expresión correcta.
Expresión del inciso E.
n=1\to 3(-1{)}^{n}+5-n=1
n=2\to 3(-1{)}^{n}+5-n=6
n=3\to 3(-1{)}^{n}+5-n=-1
La expresión del inciso E cumple con los elementos de la lista.
Concluimos seleccionando como correcta a la opción E.
Reactivo 35: Porcentajes
Juan tiene el 75% de $1650, Antonio el 48% de $625 y Roberto el 33% de $827 ¿Cuánto dinero tienen entre los tres?
- $1400.51
- $1539.41
- $1700.39
- $1810.41
- $1901.31
Solución:
Para determinar el dinero que tienen entre los tres, debemos calcular el 75% de $1650, el 48% de $625 y el 33% de $827. El total será la suma de los resultados.
Total=\%Juan+\%Antonio+\%Roberto
El porcentaje de una x cantidad, se determina multiplicando a x por el porcentaje \% dado y luego dividiendo el resultado entre 100.
Total=\frac{\$1650*75\%}{100}+\frac{\$625*48\%}{100}+\frac{\$827*33\%}{100}=\$1810.41
Entre los tres tienen $1810.41.
Comparando con las opciones, seleccionamos como correcta a la D.
Reactivo 36: Relaciones directas
Un auto puede recorrer 180 km con 12 litros de gasolina ¿Qué distancia puede recorrer con 20 litros de gasolina?
- 350 km
- 280 km
- 325 km
- 300 km
- 200 km
Solución:
Antes de realizar la regla de tres, debemos identificar si la relación entre los kilómetros recorridos y la gasolina en el tanque es lineal o inversa. Por simple lógica, mientras mayor gasolina tenga el auto más kilómetros podrá recorrer, por ende es una relación lineal.
Regla de tres lineal.
12 L\to 180 km
20 L\to x
x=\frac{20 L\bullet 180 km}{12 L}=300 km
El conductor podrá recorrer 300 km si tiene en el tanque 20 litros.
Seleccionamos como respuesta correcta a la opción D.
Reactivo 37: Relaciones y porcentajes
Si el 55% de los habitantes de la ciudad tiene automóvil y las 2/5 partes de ellos no lo utilizan el fin de semana ¿Qué porcentaje de los habitantes si utiliza auto el fin de semana?
- 45%
- 88%
- 22%
- 33%
- 67%
Solución:
Si la proporción de habitantes que no usan automóvil el fin de semana es 2/5, quienes sí lo utilizan son el 3/5 restante. Debemos multiplicar el 55% por 3/5 para obtener el porcentaje de habitantes que si utilizan auto el fin de semana.
P=55\%\bullet \frac{3}{5}=33\%
El 33% de los habitantes tienen automóvil y lo utilizan el fin de semana.
Comparando con las opciones, la respuesta correcta es la D.

