Guía UAM CAD: Ciencias y artes para el diseño | Matemática resueltos

¡Saludos aspirante! En este tutorial vamos a resolver la guía de reactivos de matemáticas, desde el 51 hasta el 65, para la división de Ciencias y Artes para el Diseño (CAD) del examen de admisión a la Universidad Autónoma Metropolitana.

Como advertimos al principio de todas nuestras guías ¡resuelve los reactivos por tu cuenta! La única forma de obtener la calificación que deseas es mediante la práctica.

Resumen convocatoria UAM 2022.

Estructura del examen de ingreso UAM 2022

El examen de ingreso a la UAM se compone de dos pruebas: la de aptitud y la de conocimientos específicos. La primera es igual para todas las divisiones y posee reactivos de razonamiento matemático y razonamiento verbal, con una extensión total de 40 reactivos.

La segunda, varía en función a la división de tu carrera. Para el caso de aquellas que pertenecen a Ciencias y Artes para el Diseño, las asignaturas son: física, arte universal, arte en México, dibujo y modelado.

La siguiente lista muestra los sub temas en cada una de las asignaturas ya mencionadas.

Fundamentos de física

• Cinemática.
• Dinámica.
• Estática.
• Contexto histórico

El arte universal

• Grecia y Roma.
• Edad media.
• Renacimiento.
• Siglo XIX y XX.
• Contemporáneo.

El arte en México

• Prehispánico.
• Colonial.
• Independiente.
• Revolucionario.
• Contemporáneo.

Dibujo y modelado

• Dibujo y modelado
• Tipos de líneas.
• Formas geométricas planas.
• Representación.
• Perspectiva.
• Escalas, ejes y cotas, calidad de línea.
• Textura.
• Relieve.
• Formas volumétricas.

Resumen de reactivos en cada parte del examen.

Área	Reactivos	Porcentaje
Razonamiento verbal	20	25%
Razonamiento matemático	20	25%
Conocimientos específicos	40	50%
Total	80	100%

Temario de Matemáticas para CAD

El temario se presenta de forma resumida en la guía de la división en cuestión, te recomiendo apoyarte en la bibliografía indicada por la UAM en dicha guía para complementar lo aprendido.

• Aritmética.
• Álgebra.
• Geometría euclidiana.
• Trigonometría.
• Geometría analítica.
• Teoría de conjuntos.

Guía UAM CAD de Matemáticas resuelta

Luego de esta introducción, vamos con la solución paso a paso de la guía de ejercicios de matemáticas. No olvides visitar nuestro canal de youtube, allí encontrarás material audiovisual gratuito sobre guías y maratones en vivo de reactivos.

Reactivo 51: Problemas con fracciones

¿Cuál es el número qué es las \frac{2}{3} partes de \frac{1}{2} del doble de 6?

1. 4
2. 5
3. 10
4. 6
5. 2

Solución:

Debemos calcular el valor de un número cualquiera x , que es igual a la relación entre números fracciones, indicada por el enunciado.

En este tipo de problemas, debemos resolver desde el final hacia el inicio. Comenzamos con doble de 6:

2*6=12

Ahora, vamos con \frac{1}{2} del doble:

\frac{1}{2}*12=6

Finalmente, con las \frac{2}{3} partes de:

\frac{2}{3}*6=4

De esta forma, dicho número x es igual a 4.

Comparando con las opciones, seleccionamos como correcta a la A.

Reactivo 52: Problemas aritméticos

Elige el número que al dividirse entre 80 dé como resultado \frac{3}{5}

1. 123\frac{1}{2}
2. 130
3. 129
4. 133\frac{1}{3}
5. 143

Solución:

En este caso, debemos calcular un número x tal que, al dividirse entre 80 \frac{80}{x} sea igual a la fracción \frac{3}{5} . Lo anterior se puede expresar mediante la siguiente igualdad:

\frac{80}{x}=\frac{3}{5}

Simplificamos.

x=\frac{80}{\frac{3}{5}}

Aplicamos la regla de la doble tortilla o doble c.

x=\frac{5*80}{3}=\frac{400}{3}

Ya que algunas de las opciones están expresadas en fracción mixta, debemos convertir nuestro resultado a esa forma. Realizamos el cociente entre el numerador y el denominador, quedando:

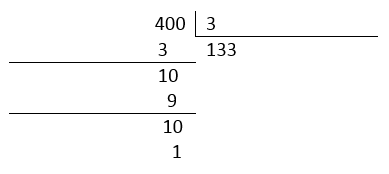
Finalmente:

x=\frac{400}{3}=133\frac{1}{3}

Comparando con las opciones, la respuesta correcta sería la D.

Reactivo 53: Regla de tres inversa

Un grupo de obreros han hecho una obra en 20 días trabajando 6 horas diarias ¿En cuántos días terminarán la misma obra si trabajan 8 horas diarias?

1. 8
2. 8
3. 15
4. 6
5. 20

Solución:

Para calcular el número de días que tardarían al trabajar 8 horas diarias, debemos establecer una regla de tres inversa, ya que mientras más horas al día trabajen los obreros, menor será la cantidad de días que tardaran en culminar la obra.

x=\frac{6 horas*20 dias}{8 horas}=15 dias

El grupo de obreros terminaría en 15 días si trabaja 8 horas diarias.

Finalizamos el ejercicio seleccionando como correcta a la opción C.

Reactivo 54: Radicales

La expresión 3\sqrt{4} es igual a:

1. {4}^{2}\sqrt{2}
2. 2
3. 6
4. 8
5. \sqrt[3]{9}

Solución:

En la expresión con radical dada, sabemos que la raíz cuadrada de 4 es 2, por tanto:

3\sqrt{4}=3*2

Multiplicamos el 3 con el dos para obtener el resultado final.

3\sqrt{4}=6

Concluimos que:

La expresión 3\sqrt{4} es igual a 6.

Comparando con las opciones, queda claro que la respuesta correcta es la C.

Reactivo 55: Sistema de ecuaciones lineal

En el siguiente sistema de ecuaciones, el valor de x es:

\left\{\begin{array}{c}x=12-y \\ y-9=-\frac{15}{2}\end{array}\right.

1. 2
2. 3
3. \frac{1}{2}
4. \frac{21}{2}
5. 0

Solución:

Emplearemos el método por sustitución, ya que en la segunda ecuación podemos despejar el valor de y y con el sustituir en la segunda ecuación para encontrar a x .

Despejando a y .

y-9=-\frac{15}{2}\to y=9-\frac{15}{2}

\therefore y=\frac{3}{2}

Sustituimos en la primera ecuación.

x=12-\left(\frac{3}{2}\right)=12-\frac{3}{2}

\therefore x=\frac{21}{2}

El valor de x es \frac{21}{2} .

Comparando con las opciones, la respuesta correcta es la D.

Reactivo 56: Productos notables

Al desarrollar la expresión (5a-2b{)}^{2} se obtiene:

1. 5{a}^{2}-2{b}^{2}
2. 25{a}^{2}-4{b}^{2}
3. 25{a}^{2}-20ab+4{b}^{2}
4. 5{a}^{2}-2ab+2{b}^{2}
5. 5{a}^{2}+2ab+2{b}^{2}

Solución:

Para desarrollar esta expresión, empleamos el producto notable para el cuadrado de la diferencia de dos números:

{\left(x-y\right)}^{2}={x}^{2}-2xy+{y}^{2}

En este caso x=5a y y=2b . Sustituimos en el producto notable:

(5a-2b{)}^{2}={\left(5a\right)}^{2}-2\left(5a\right)\left(2b\right)+{\left(2b\right)}^{2}

Simplificamos.

(5a-2b{)}^{2}=25{a}^{2}-20ab+4{b}^{2}

Concluimos que:

Al desarrollar la expresión (5a-2b{)}^{2} se obtiene 25{a}^{2}-20ab+4{b}^{2} .

Comparando con las opciones, seleccionamos como correcta a la C.

Reactivo 57: Clasificación de triángulos

Si los lados de un triángulo miden 3 cm, 4 cm y 5 cm, el triángulo es:

1. Isósceles
2. Rectángulo
3. Acutángulo
4. Equilátero
5. Obtusángulo

Solución:

Antes de pasar a analizar si los términos de cada inciso corresponden o no con la información suministrada, podemos descartar ciertas opciones.

Por ejemplo, el triángulo no puede ser ni equilátero ni isósceles, porque ni tres ni dos de los lados miden igual. Quedan entonces descartados los incisos A y D.

Lo siguiente que podemos hacer, es aplicar el teorema de Pitágoras para comprobar si el triángulo es o no rectángulo. Elevamos el lado más largo al cuadrado y si es igual a la suma de los cuadrados de los otros dos, entonces es rectángulo.

Lado más largo.

{5}^{2}=25

Suma de los cuadrados de los otros dos.

{3}^{2}+{4}^{2}=9+16=25

¡Son iguales!

{5}^{2}={3}^{2}+{4}^{2}

El triángulo es rectángulo.

Seleccionamos como correcta la opción B.

Reactivo 58: Características de los triángulos

Cuando una bisectriz y una altura en un triángulo coinciden, este es:

1. Obtusángulo
2. Acutángulo
3. Rectángulo
4. Escaleno
5. Isósceles

Solución:

Una bisectriz en un triángulo, es un segmento de recta que va desde un vértice, parte el ángulo en dicho vértice a la mitad y toca en algún punto al lado opuesto.

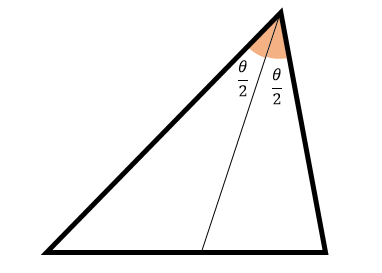
Por otro lado, una altura es un segmento de recta que va desde un vértice y es perpendicular al lado opuesto.

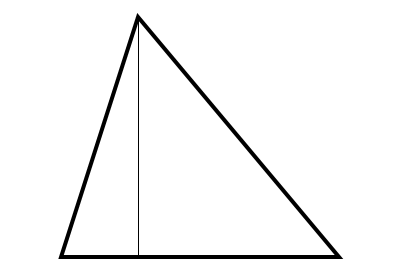
Para que una altura y una bisectriz sean iguales, el triángulo debe ser isósceles. De esta manera, si se traza una altura desde el vértice que une a los dos lados iguales, hacia el lado opuesto, dicho segmento también parte al ángulo del vértice en dos partes iguales.

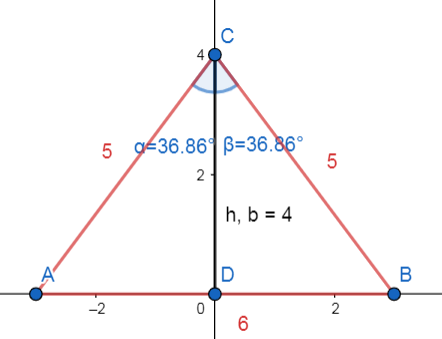
En un triángulo equilátero, las tres alturas son iguales a las tres bisectrices. Concluimos indicando como respuesta correcta a la opción E.

Reactivo 59: Teorema de Pitágoras

Si en un triángulo rectángulo la hipotenusa vale \sqrt{11} y uno de sus catetos 1, ¿Cuánto vale el otro cateto?

1. 9
2. 10
3. \sqrt{10}
4. \sqrt{5}
5. 4

Solución:

Aplicamos el teorema de Pitágoras para calcular el valor del otro cateto:

{h}^{2}={a}^{2}+{b}^{2}

El cateto puede ser a o b , ya que el teorema no distingue entre catetos sino entre la hipotenusa y los catetos; además la suma es conmutativa. Escogeremos esta vez a b como la incógnita.

{b}^{2}={h}^{2}-{a}^{2}

b=\sqrt{{h}^{2}-{a}^{2}}

Sustituimos.

b=\sqrt{{\left(\sqrt{11}\right)}^{2}-{1}^{2}}=\sqrt{11-1}=\sqrt{10}

El otro cateto vale \sqrt{10} unidades.

Seleccionamos la opción C como la respuesta correcta.

Reactivo 60: Ecuación de la circunferencia

La ecuación de la circunferencia con centro en el punto \left(-2, 3\right) y radio 4 es:

1. {x}^{2}-3x+{y}^{2}=3
2. {x}^{2}+{y}^{2}+4x-6y=3
3. {x}^{2}+3{y}^{2}=9
4. x-y-6=16
5. -{x}^{2}+{y}^{2}-6=3

Solución:

El ejercicio nos solicita la ecuación general de la circunferencia con centro en \left(-2, 3\right) y radio igual a 4. Debemos sustituir ambos valores en la ecuación ordinaria de la circunferencia y desarrollar para obtener la general.

{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}

Sustituimos las coordenadas del centro \left(h,k\right)=\left(-\mathrm{2,3}\right) y el radio r=4 .

{\left(x+2\right)}^{2}+{\left(y-3\right)}^{2}=16

Desarrollamos.

{x}^{2}+4x+4+{y}^{2}-6y+9=16

{x}^{2}+{y}^{2}+4x-6y=3

Comparando con las opciones, la respuesta correcta es la opción B.

Reactivo 61: Secciones cónicas y sus ecuaciones

La ecuación \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1 representa una:

1. Hipérbola
2. Circunferencia sobre el eje de las y
3. Elipse
4. Parábola
5. Paraboloide

Solución:

La ecuación del ejercicio representa a una elipse. No puede ser una circunferencia porque los parámetros a y b son diferentes, tampoco una hipérbola porque uno de los términos del primer miembro tendría que estar negativo y tampoco una parábola, porque ambas variables, x y y están elevadas al cuadrado.

Finalizamos el problema seleccionando como respuesta correcta a la opción C.

Reactivo 62: Ecuación de la recta

La ecuación de la recta cuya pendiente es igual a 3 y pasa por el punto P\left(\mathrm{5,2}\right) es:

1. y=3x
2. y=3x+5
3. y=3x+7
4. y=3x-13
5. y=3x+13

Solución:

Debemos emplear la ecuación punto-pendiente para resolver el ejercicio. En ella, sustituimos las coordenadas del punto que pertenece a la recta y el valor de la pendiente.

y-{y}_{o}=m\left(x-{x}_{o}\right)

P\left({x}_{o},{y}_{o}\right)=P\left(\mathrm{5,2}\right) y m=3

Sustituyendo.

y-2=3\left(x-5\right)

Despejamos a y .

y-2=3x-15\to y=3x-15+2

y=3x-13

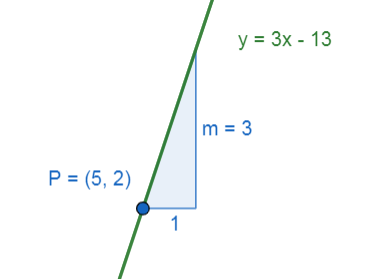
Seleccionamos como respuesta correcta a la opción D.

Reactivo 63: Ordenamiento de números reales

Dados los números \sqrt{2},\frac{2}{13},\frac{1}{4},\frac{5}{3},\frac{9}{8} el de mayor valor es:

1. \frac{5}{3}
2. \frac{2}{13}
3. \frac{1}{4}
4. \frac{9}{8}
5. \sqrt{2}

Solución:

Ya que tenemos una mezcla de números fraccionarios con radicales, debemos:

1. Hacer que todos tengan el mismo denominador (hay que calcular el mcm)
2. Expresarlos a todos como radicales

Comenzamos por calcular el mcm de los denominadores de todos los números.

mcm\left(\mathrm{1,13,4},\mathrm{3,8}\right)=312

Multiplicamos y dividimos cada fracción por un número tal que en el denominador de como resultado 312.

Fracción 1.

\frac{312\sqrt{2}}{312}

Fracción 2.

x=\frac{312}{13}=24\to \frac{2}{13}*\frac{24}{24}

\frac{48}{312}

Fracción 3.

x=\frac{312}{4}=78\to \frac{1}{4}*\frac{78}{78}

\frac{78}{312}

Fracción 4.

x=\frac{312}{3}=104\to \frac{5}{3}*\frac{104}{104}

\frac{520}{312}

Fracción 5.

x=\frac{312}{8}=39\to \frac{9}{8}*\frac{39}{39}

\frac{351}{312}

Las fracciones serían:

\frac{312\sqrt{2}}{312},\frac{48}{312}, \frac{78}{312}, \frac{520}{312}, \frac{351}{312}

Ahora, a cada número lo elevamos al cuadrado y le aplicamos raíz cuadrada. A los del numerador como a los del denominador exceptuando \sqrt{2} porque ya tiene raíz.

\frac{\sqrt{{312}^{2}}\sqrt{2}}{\sqrt{{312}^{2}}},\frac{\sqrt{{48}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{78}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{351}^{2}}}{\sqrt{{312}^{2}}}

En la primera fracción aplicamos la propiedad del producto de raíces de igual índice.

\frac{\sqrt{{312}^{2}*2}}{\sqrt{{312}^{2}}},\frac{\sqrt{{48}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{78}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}, \frac{\sqrt{{351}^{2}}}{\sqrt{{312}^{2}}}

Con los números escritos de esta forma, podemos seleccionar cual es el mayor verificando el que tenga en el numerador el radicando mayor. Podemos descartar a {48}^{2} y {78}^{2} porque son significativamente menores al resto.

Como {351}^{2} y {312}^{2} son números muy cercanos, podemos descartar a {351}^{2} porque {312}^{2} está multiplicado por dos. Solo quedan {520}^{2} y {312}^{2}*2 , podemos incluir el 2 dentro de la potencia si lo expresamos como:

{312}^{2}*{\sqrt{2}}^{2}={\left(312*\sqrt{2}\right)}^{2}

Ahora, \sqrt{2} es aproximadamente 1.414.

{\left(312*\sqrt{2}\right)}^{2}\approx {\left(312*1.414\right)}^{2}

Este producto es más sencillo de realizar y es igual a:

{\left(312*1.414\right)}^{2}={441.168}^{2}

La potencia {441.168}^{2} es menor que {520}^{2} , por tanto concluimos que el número mayor es:

\frac{\sqrt{{520}^{2}}}{\sqrt{{312}^{2}}}=\frac{520}{312}=\frac{5}{3}

Concluimos entonces que la respuesta correcta es la opción A. Este procedimiento evita en todo momento el uso de la calculadora. Otra forma habría sido encontrar el valor decimal de las fracciones y del radical, para compararlos.

Reactivo 64: Porcentajes

¿De qué número es 196 el 0.56%?

1. 100000
2. 35000
3. 128000
4. 19600
5. 40000

Solución:

Para resolver este problema, emplearemos la fórmula para calcular el porcentaje de una cantidad respecto de otra.

N=\frac{\%*{N}_{r}}{100\%}

Donde N es el resultado del porcentaje y {N}_{r} es la cantidad de referencia o a la que le queremos calcular el porcentaje. En nuestro caso 196 es el resultado obtenido, es decir N y lo que nos piden es a {N}_{r} . Debemos despejar a {N}_{r} de la fórmula.

N=\frac{\%*{N}_{r}}{100\%}\to {N}_{r}=\frac{100\%*N}{\%}

Sustituimos los valores dados.

{N}_{r}=\frac{100\%*\left(196\right)}{0.56\%}=\mathrm{35,000}

Finalmente, el número del que 196 es el 0.56% es 35000.

Concluimos seleccionando como correcta a la opción B.

Reactivo 65: Conjuntos y subconjuntos

La proposición que describe un subconjunto del conjunto \left\{1, 2, 3, 4, 5, 6, 7, 8, 9\right\} es:

1. x es mayor que 9
2. x es equivalente a \frac{2}{3}
3. 23=9+x
4. Los enteros positivos menores que 8
5. x es menor que 1

Solución:

Debemos analizar la proposición en cada inciso y si la misma corresponde a un subconjunto numérico de \left\{1, 2, 3, 4, 5, 6, 7, 8, 9\right\} , entonces esa será la respuesta correcta al problema.

Proposición A: x es mayor que 9.

Esta no puede ser la respuesta correcta, porque el conjunto llega hasta 9 y la proposición alude a los números 10 diez en adelante.

Proposición B: x es equivalente a \frac{2}{3} .

El conjunto del enunciado pertenece a los enteros, mientras que la proposición indica un número fraccionario \frac{2}{3} por tanto, tampoco es un subconjunto.

Proposición C: 23=9+x .

Si despejamos a x de la ecuación nos queda x=14 y dicho número no pertenece al conjunto. Esta proposición no es subconjunto del conjunto.

Proposición D: Los enteros positivos menores que 8.

Respecto al conjunto, los enteros menores que 8 serian \left\{1, 2, 3, 4, 5, 6, 7\right\} y este si es subconjunto de \left\{1, 2, 3, 4, 5, 6, 7, 8, 9\right\} . La opción D es la respuesta correcta al ejercicio.

La última proposición indica los números menores que 1 pero el conjunto tiene como elemento menor a 1, por tanto tampoco es correcta. En conclusión, seleccionamos como respuesta correcta a la opción D.