La UABC tiene una nueva guía de estudios, y un nuevo formato de examen llamado ExIES (Examen de Ingreso a la Educación Superior), en este artículo vamos a resolver los ejercicios muestra de matemáticas que vienen en la guía.

¿Qué tan difícil es la parte de matemáticas? En general suele ser la más complicada debido a la gran cantidad de temas, específicamente en el examen de la UABC deberás resolver 50 ejercicios provenientes de todas las materias que cursaste la preparatoria.
¿Cómo es el nuevo examen?
El nuevo examen de ingreso a UABC consta de 160 reactivos, de los cuales 38 son de prueba, y 122 son con los que determinaran tu puntaje final.
Abarca tres materias que te mostraré a continuación con la estructura del examen:
| ÁREAS | PREGUNTAS |
|---|---|
| Lectura | 36 |
| Lengua Escrita | 36 |
| Matemáticas | 50 |
| Preguntas evaluativas | 122 |
| Preguntas piloto | 38 |
| TOTAL | 160 |
Quitando las preguntas piloto, el examen de admisión, incluyendo la materia de matemáticas, quedaría de la siguiente forma:
- Matemáticas: 50 reactivos
- Lectura: 36 reactivos
- Lengua escrita: 36 reactivos
Es decir que la parte de matemáticas tiene un gran peso en el examen, eso no quiere decir que debes dejar de lado las otras dos materias (siendo justos la parte que pesa más es la de español).
Temario de matemáticas
Son bastantes los temas que tienes que estudiar, como te comente en un principio, prácticamente vienen todas las materias referentes a área en cuestión que cursaste durante tu bachillerato.
| Contenido | Reactivos |
|---|---|
| Herramientas Algebraicas: Resolución de problemas mediante el empleo de ecuaciones y sistemas lineales, ya sea a través de la representación de cantidades o de la representación gráfica | 10 |
| Problemas, Probabilidad y Análisis de Datos: Creación y análisis de relaciones, representación y análisis de datos cuantitativos y aplicación de probabilidades | 15 |
| Matemáticas Avanzadas: Creación de expresiones algebraicas y uso de gráficos que representan funciones exponenciales no lineales o cuadráticas | 15 |
| Temas Adicionales en Matemáticas: Solución de problemas asociados al área y volumen, aplicación de definiciones, teoremas sobre líneas, ángulos, triángulos y círculos | 10 |
| Total | 50 |
- Herramientas algebraicas.
- Planteamiento de una ecuación lineal con una variable mediante un contexto.
- Interpretación y solución de inecuaciones lineales con una variable.
- Construcción de una función lineal que represente la relación lineal entre dos variables.
- Interpretación y resolución de un sistema de ecuaciones lineales con tres variables.
- Interpretación y resolución de un sistema de ecuaciones lineales con dos variables.
- Resolución de ecuaciones lineales en una variable.
- Resolución de sistemas de ecuaciones lineales con dos variables.
- Interpretación de las características de una función lineal dentro de un contexto.
- Relación entre la representación gráfica y algebraica de una función lineal.
- Problemas, probabilidad y análisis de datos.
- Resolución de problemas utilizando índices, tasas, relaciones proporcionales y dibujos a escalas mediante uno o varios pasos.
- Resolución de problemas utilizando porcentajes con uno o varios pasos.
- Resolución de problemas utilizando diferentes magnitudes, y diferentes sistemas de unidades.
- Análisis de variables involucradas en los diferentes modelos lineales, cuadráticos y exponenciales.
- Identificación de las características claves de un gráfico utilizando la relación entre las dos variables.
- Calcular frecuencias relativas y probabilidades (sumativa y multiplicativa).
- Realizar inferencias a partir de los datos de una muestra.
- Obtención de las medidas de tendencia central de datos y medidas de dispersión.
- Analizar reportes para hacer inferencias a partir de una tabla estadística.
- Matemáticas avanzadas.
- Resolver problemas mediante funciones cuadráticas y exponenciales.
- Traducir contextos de lenguaje escrito a lenguaje algebraico.
- Convertir expresiones algebraicas con exponentes racionales a radicales y viceversa.
- Convertir ecuaciones de la forma ordinaria a la forma general y viceversa.
- Resolver ecuaciones cuadráticas.
- Simplificar operaciones aritméticas con polinomios.
- Resolver ecuaciones radicales y racionales en una variable.
- Resolución de un sistema de ecuaciones lineal y cuadrática.
- Simplificación de expresiones algebraicas (fracciones) complejas.
- Interpretación de parámetros, constantes o variables de una expresión no lineal en términos de un contexto dado.
- Comprensión y determinación de ceros y factores de polinomios para la elaboración de gráficos.
- Análisis de variables de expresiones algebraicas y su relación directa con el sistema de representación gráfico (sistemas de ecuaciones, descripción verbal del comportamiento gráfico, determinación de puntos importantes de una gráfica).
- Uso de notación de funciones e interpretación del significado de dichas notaciones (evaluación de funciones).
- Comprensión de las formas general, estándar o canónica de expresiones algebraicas para identificar parámetros de interés (vértice, ordenada en el origen).
- Temas adicionales en matemáticas.
- Resolución de problemas que incluyan el cálculo de áreas o volúmenes de figuras geométricas.
- Uso de proporción trigonométrica y el Teorema de Pitágoras para resolver distintos problemas que consideran triángulos rectángulos.
- Resolución de triángulos oblicuángulos mediante ley de senos y ley de cosenos.
- Conversión entre grados y radianes y uso de radianes para determinar la longitud del arco; usar funciones trigonométricas en escala de radianes.
- Aplicación de teoremas sobre círculos para encontrar la longitud del arco, medidas de ángulos, longitud de la cuerda y áreas de un sector.
- Uso de conceptos y teoremas sobre congruencia y similitud para resolver problemas sobre líneas, ángulos y triángulos.
- Uso de la relación entre similitud, triángulo-rectángulo y proporciones trigonométricas; usar la relación entre seno y coseno de ángulos complementarios.
- Elaboración o uso de una ecuación en dos variables para resolver problemas sobre un círculo en un plano cartesiano.
Ejercicios de matemáticas resueltos
En la guía encontrarás 5 ejercicios, muestra con los que te podrás dar una idea el tipo de reactivos que encontraras en el examen de admisión, recuerda revisar los requisitos de la convocatoria UABC 2023 para iniciar tu proceso de registro.
Reactivo 1
Alicia tiene 480 pesos en monedas de 5 y 10 pesos. Si tiene 60 monedas en total, ¿Qué ecuación determina la cantidad x de monedas de cinco pesos?
- 5x+\left(60-10\right)x=480
- 5x+\left(60-10x\right)=480
- 5x+10\left(x-60\right)x=480
- 5x+10\left(60-x\right)=480
Solución:
Iniciamos indicando al total de monedas de 5 pesos como x , mientras que el de 10 pesos como y . Por lógica, las 60 monedas deben ser iguales a la suma de las de 5 pesos con las de 10 pesos.
x+y=60
Además, los 480 pesos que suman las 60 monedas, se pueden expresar como la suma del producto del monto de la moneda por la cantidad de monedas.
5x+10y=480
Despejamos a y de la primera ecuación y lo sustituimos en la segunda.
y=60-x
5x+10\left(60-x\right)=480
La ecuación que permite determinar la cantidad x de monedas de 5 pesos es:
5x+10\left(60-x\right)=480
Comparando con los incisos, indicamos como respuesta correcta a D.
Reactivo 2
Cuando el aire asciende, se dilata y, al dilatarse, se enfría a razón de alrededor de 1° por cada 100 metros de ascenso hasta unos 12 km de altura. Si la temperatura del suelo es de unos 20°, ¿cuál es la fórmula para la temperatura T a una altura h medida en metros?
- T=\frac{h}{100}+20
- T=\frac{h+12}{100}+20
- T+1=\frac{h}{100}+20
- T+1=\frac{h+12}{100}+20
Solución:
En este caso tenemos que encontrar el modelo matemático que nos permitirá calcular la temperatura del aire en función de la altura.
Tengamos en cuenta que la frase:… Hasta unos 12 km de altura, nos dice que este modelo matemático es válido hasta los 12 kilómetros. Para alturas superiores, se debe utilizar otro modelo matemático.
Debido a que nos indican una razón en el enunciado, se debe utilizar como modelo matemático una línea recta, cuya variable independiente es la altura h e independiente la temperatura T .
T-{T}_{o}=m\left(h-{h}_{o}\right)
La pendiente o razón viene dada por el enunciado como: 1° por cada 100 metros de ascenso.
m=\frac{1}{100} \frac{°\mathrm{C}}{\mathrm{m}}
{T}_{o} y {h}_{o} son valores que pertenecen a la recta. El enunciado dice que la temperatura en el suelo, es decir 0 metros, es de 20°. Estos son los valores de {T}_{o} y {h}_{o} . Sustituimos.
T-20°=\frac{1}{100}\left(h-0\right)\to T=\frac{h}{100}+20
El modelo matemático para la temperatura del aire respecto a la altura, hasta los 12 km es:
T\left(h\right)=\frac{h}{100}+20, \forall h\in \left[0, 12000\right] \mathrm{m}
La respuesta correcta es el inciso A.
Reactivo 3
En el equipo de fútbol de la universidad se hizo una clasificación de los promedios del primer parcial de sus 20 miembros. La información se sintetizó en la siguiente tabla:
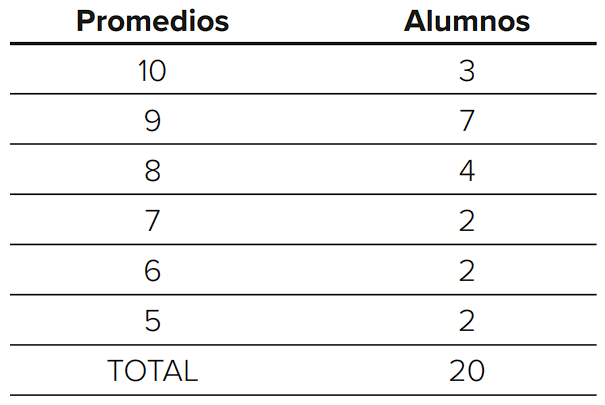
Selecciona la afirmación que concuerde con los datos obtenidos.
- Los promedios del equipo tienen una desviación estándar menor a 2.
- Los promedios del equipo tienen una desviación estándar mayor a 2.
- Los promedios del equipo tienen un rango menor a 3.
- Los promedios del equipo tienen un rango mayor a 6.
Solución:
En los incisos del reactivo se habla de desviación estándar y rango. El primero tiene un procedimiento largo para su cálculo, mientras que el segundo se obtiene mediante una simple resta.
Para evitar el cálculo de la desviación a toda costa, primero vamos a comprobar las aseveraciones respecto al rango. Si ninguna cumple, tendremos que calcular la desviación estándar. Hay que tener en cuenta que solo una pregunta es correcta, por esta razón es viable el descarte.
Cálculo del rango del conjunto de datos.
Se calcula como la diferencia entre el máximo y el mínimo de una población.
r={x}_{M}-{x}_{m}
El promedio máximo es 6 y el mínimo 5.
r=10-5=5
Ninguna de las dos aseveraciones respecto al rango es correcta. Pasamos al cálculo de la desviación típica.
Desviación típica poblacional.
s=\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}\cdot {f}_{i}}{N}}
Iniciamos calculando la media aritmética.
\stackrel{-}{x}=\frac{\left(10\right)\left(3\right)+\left(9\right)\left(7\right)+\left(8\right)\left(4\right)+\left(7\right)\left(2\right)+\left(6\right)\left(2\right)+\left(5\right)\left(2\right)}{20}
\stackrel{-}{x}=8.05
Con ayuda de una tabla, calculamos {\left({x}_{i}-\stackrel{-}{x}\right)}^{2} para cada dato.
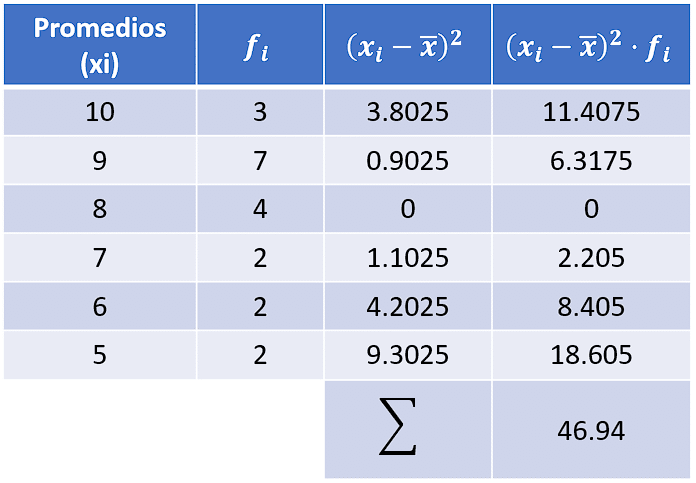
Sustituimos en la ecuación:
s=\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}\cdot {f}_{i}}{N}}=\sqrt{\frac{46.94}{20}}=\sqrt{2.347}=1.532
La desviación estándar del conjunto de datos es menor a 2.
La respuesta correcta es el inciso A.
Reactivo 4
Un proyectil es disparado hacia arriba desde una altura de 60 pies sobre el suelo. Su altura está dada por la siguiente ecuación cuadrática:
h\left(t\right)=-4{t}^{2}+8t+19
Con base en esta función, ¿cuál es la altura del proyectil en un tiempo de 3 segundos?
- 7 pies
- 53 pies
- 60 pies
- 67 pies
Solución:
Para obtener la altura del proyectil en t=3 \mathrm{s} , sustituimos a t por 3.
h\left(t=3\right)=-4{\left(3\right)}^{2}+8\left(3\right)+19
h\left(t=3\right)=-4\left(9\right)+24+19=7 \mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}
La respuesta correcta es el inciso A.
Reactivo 5
En el plano de construcción de un túnel parabólico se ubica el vértice en la coordenada V(2, 5) y el foco en F(2, 3), ¿cuál es la ecuación general del trazado parabólico que define la construcción del túnel?
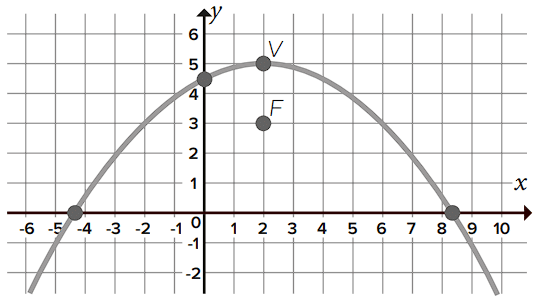
- {x}^{2}-4x+8y-36=0
- {x}^{2}-4x-8y+44=0
- {x}^{2}-4x+12y-44=0
- {x}^{2}-4x+12y-54=0
Solución:
La parábola que se muestra en la figura tiene el eje focal vertical y abre hacia abajo. La ecuación ordinaria es:
{\left(x-h\right)}^{2}=-4p\left(y-k\right)
Donde \left(h, k\right) son las coordenadas del vértice, es decir: \left(2, 5\right) .
{\left(x-2\right)}^{2}=-4p\left(y-5\right)
El valor de p es la distancia entre el vértice y el foco.
p=d\left(V,F\right)=\sqrt{{0}^{2}+{\left(5-3\right)}^{2}}=2
Sustituimos.
{\left(x-2\right)}^{2}=-4\left(2\right)\left(y-5\right)
{\left(x-2\right)}^{2}=-8\left(y-5\right)
Ahora, desarrollamos.
{x}^{2}-4x+4=-8y+40
{x}^{2}-4x+8y-36=0
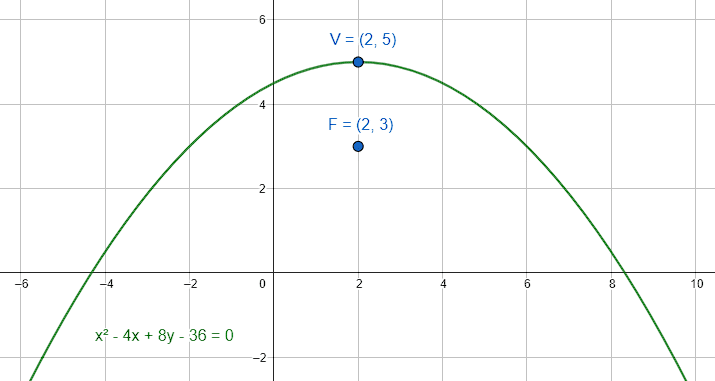
La respuesta correcta es el inciso A.

