Guía IPN 2023 Pensamiento Matemático | Parte 3 resuelta

¡Hola de nuevo, aspirante! Vamos con la solución de la guía de pensamiento matemático en la guía del IPN 2023. En este caso, vamos a desarrollar paso a paso los reactivos desde el 21 hasta el 30.

¿Te parece difícil algún reactivo? ¡No te preocupes! En cada solución te mencionamos algunos de los hacks que explicamos en el curso. Únete al curso y accede a contenido exclusivo.

Reactivo 21

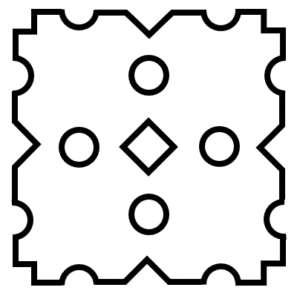
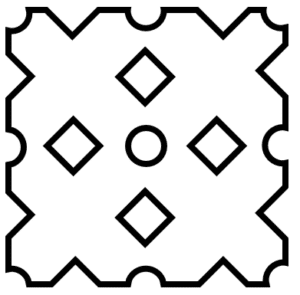
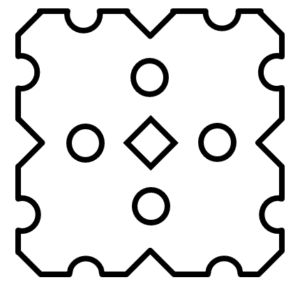
Elegir la figura que debe ocupar el espacio en blanco de la siguiente secuencia.

1. 
2. 
3. 
4. 

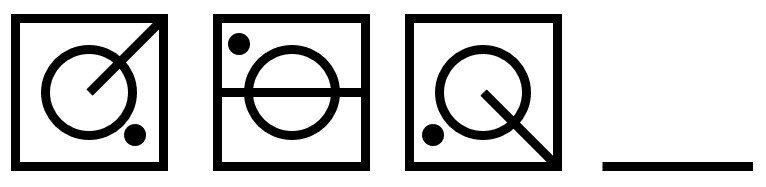
Solución:

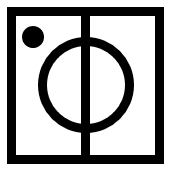
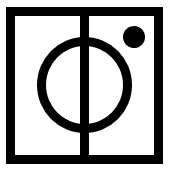
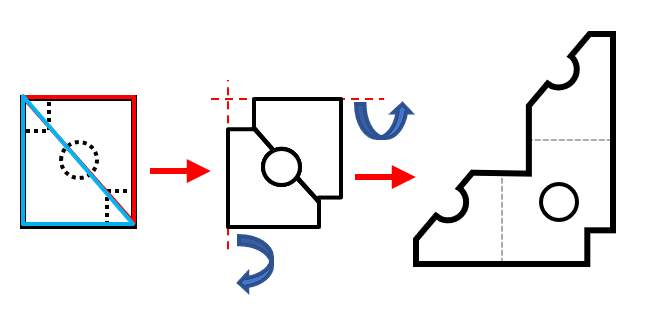
Iniciamos identificando los elementos que cambian entre los términos de la serie gráfica. Tenemos al punto, que rota 180° entre figura y figura.

Por otro lado, se visualiza una línea recta que gira 90° entre elementos consecutivos, pero con una característica adicional: cuando es oblicua, la recta va desde el centro a una esquina, pero cuando es vertical u horizontal, toca las aristas del cuadrado.

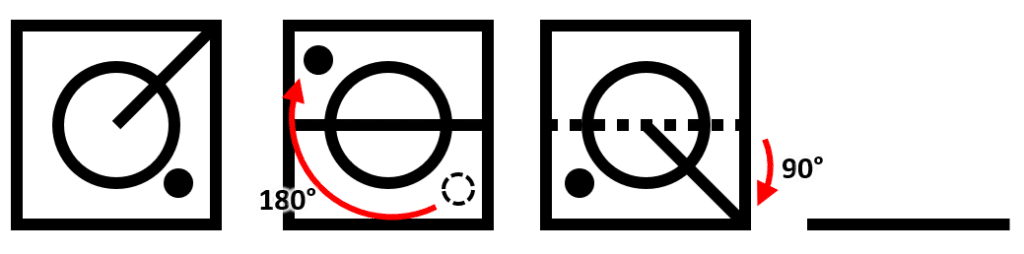
Con esta información, sabemos que el círculo debe estar en la esquina superior derecha y que la recta debe ser horizontal y completa.

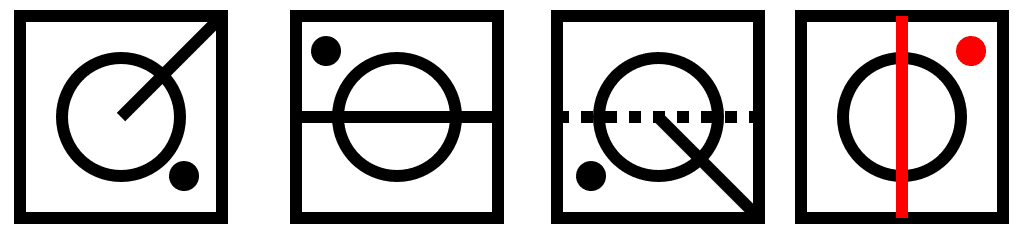
Concluimos indicando como respuesta correcta al inciso c).

Reactivo 22

Completar la secuencia

1. 
2. 
3. 
4. 

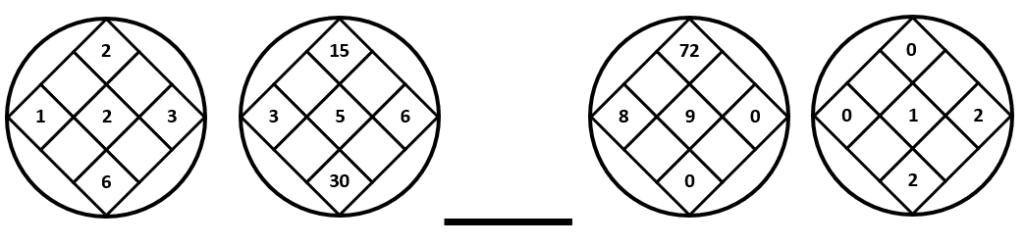
Solución:

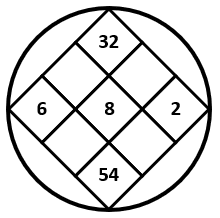
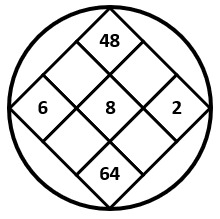
Examinando los términos de la serie gráfica, vemos que los números de la esquina superior e inferior, se encuentran al multiplicar el número del centro por el número de la izquierda y derecha, respectivamente.

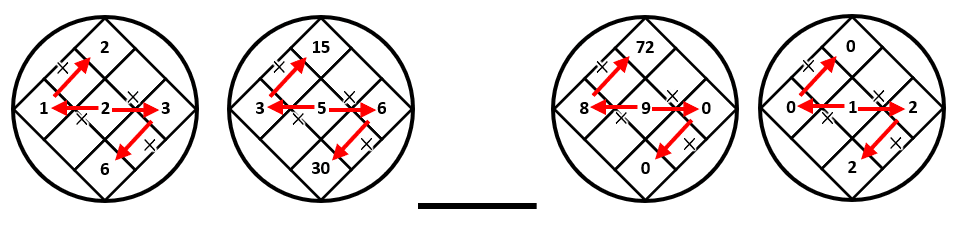
Debemos identificar cuál de las imágenes de los incisos cumple con esto. Vamos con la imagen del inciso a.

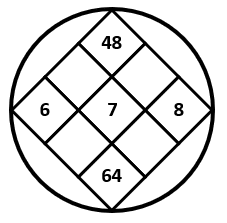
El producto de 7 con 6 no es 48. Descartamos el inciso a. Vamos con la figura b.

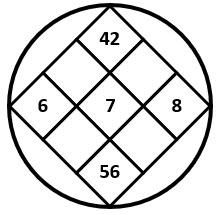
El producto de 7 con 6 es 42 y el producto de 7 con 8 es 56. Concluimos que la figura que completa la serie gráfica es la del inciso b).

Reactivo 23

En el siguiente arreglo se observan casillas con las letras A, B, C y D:

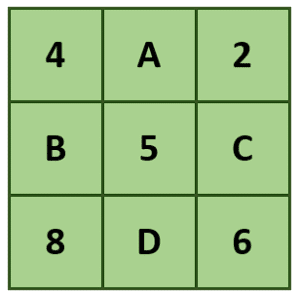
Elegir los cuatro números que pueden sustituirlas de tal forma que la suma vertical, horizontal y diagonal de todos los dígitos en el arreglo sea igual a 15.

1. 7, 9, 3, 2
2. 9, 8, 2, 1
3. 9, 3, 7, 1
4. 8, 9, 1, 2

Solución:

En este caso podemos hacer una de dos cosas: buscar los números iterando o podemos probar uno a uno los valores de los incisos. En el examen, la segunda opción es la más rápida y esta será la forma en que resolveremos el problema.

Números del inciso a).

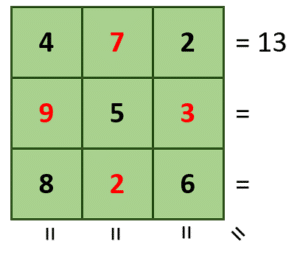
Con solo resolver la primera fila, descartamos al inciso a).

Números del inciso b).

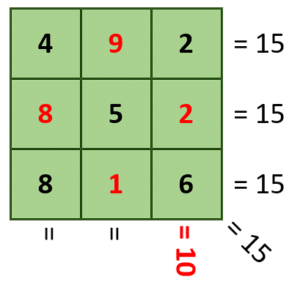
Resolviendo la tercera columna, nos damos cuenta que el inciso b) no es la respuesta correcta.

Números del inciso c).

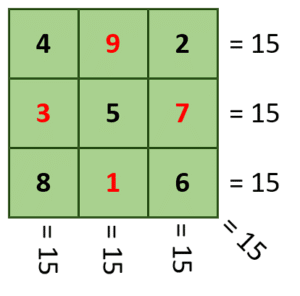
Los números del inciso c) cumplen con la condición de sumar 15 en todas las direcciones. La respuesta correcta es el inciso c).

Reactivo 24

Ordenar únicamente las rotaciones que se necesita aplicar en la Figura A para llegar a la orientación que presenta la Figura B:

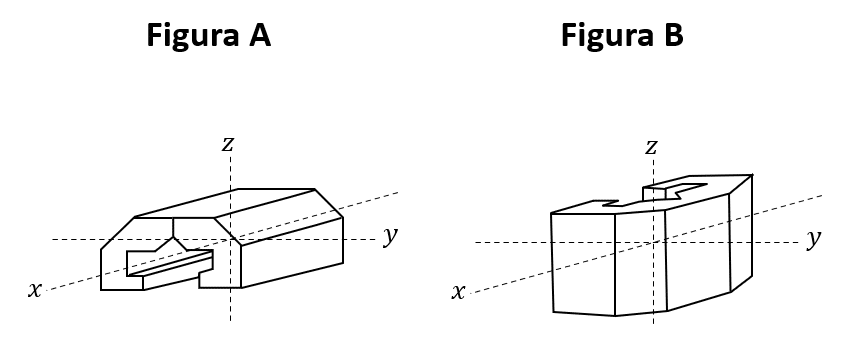
1. 90° alrededor del eje y
2. 180° alrededor del eje x
3. 180° alrededor del eje z
4. 90° alrededor del eje x
5. 90° alrededor del eje x
6. 90° alrededor del eje y

 

1. 2, 5, 6
2. 4, 3, 2
3. 4, 1, 3
4. 2, 6, 4

Solución:

En este tipo de problemas en los que hay que encontrar perspectivas o rotaciones de un cuerpo tridimensional, debes tener muy presente las características del objeto en todas sus caras.

La clave en este caso es observar que en la figura A la cara frontal tiene una línea vertical y en la figura B no se visualiza esta marca.

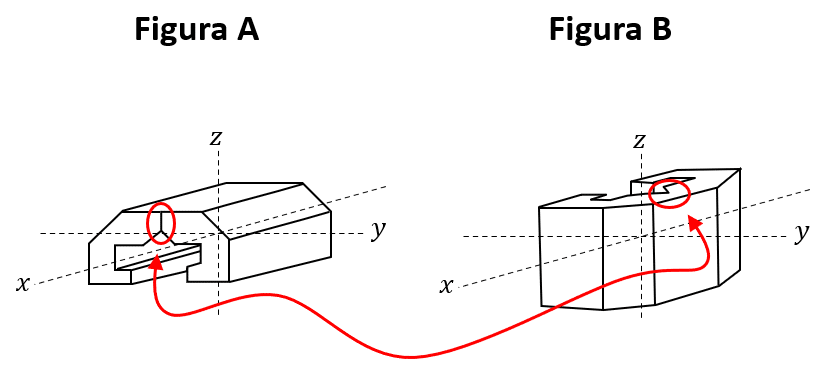
Con esto podemos asumir que la cara posterior del objeto en la figura A no tiene la marca y esa es la que debemos colocar hacia arriba. Problemas de este estilo no vas a presenciar en el examen, la intención es ejercitar tu razonamiento espacial.

Antes de continuar, veamos que las rotaciones enumeradas son todas positivas. En los ejes x , y y z ocurren rotaciones positivas en los sentidos que se señalan a continuación.

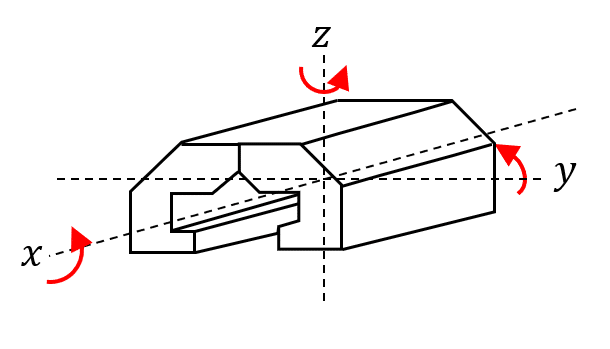
Vamos a comprobar una a una las rotaciones en los incisos. Vamos con las rotaciones del inciso a.

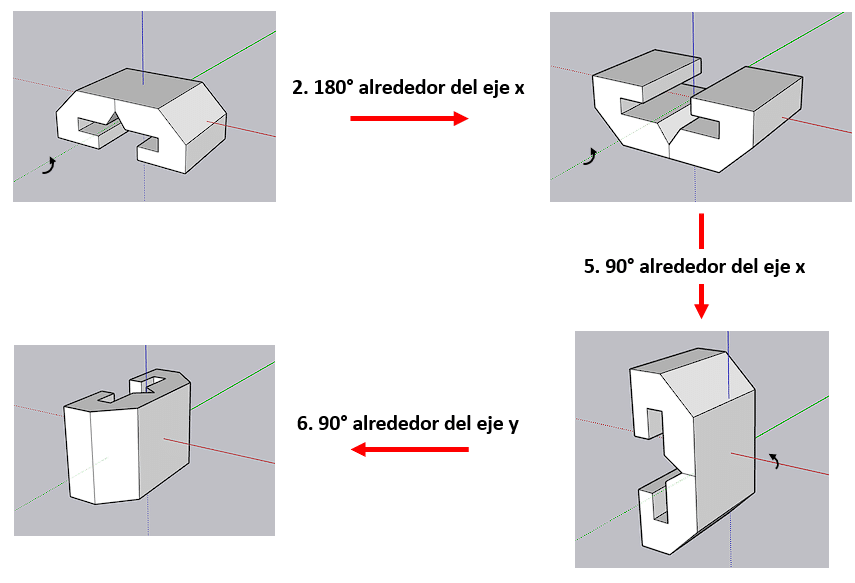
Esta combinación de rotaciones nos lleva a la figura B, pero no es la respuesta correcta al problema. La guía establece que la respuesta correcta es el inciso c). Veremos si esta combinación de rotaciones es correcta también.

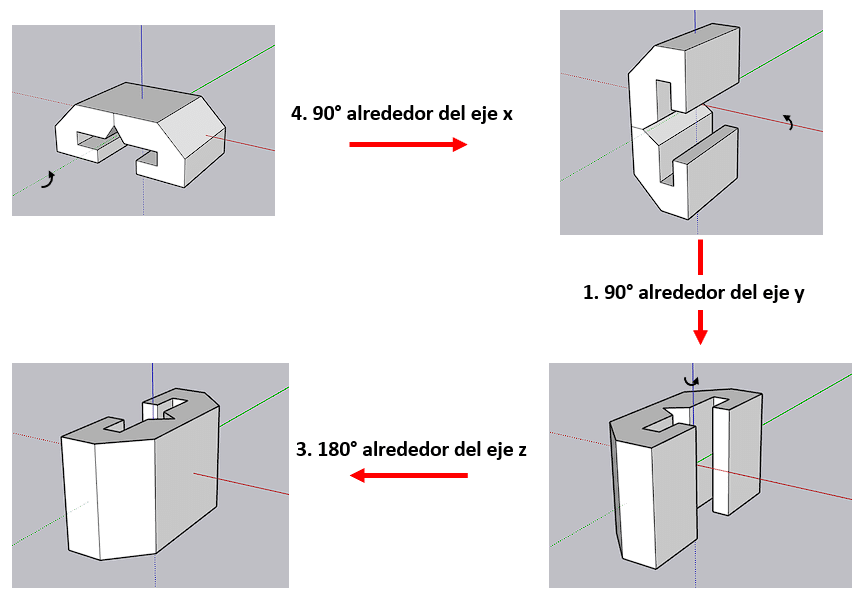
El problema tiene dos respuestas correctas: a) y c).

Reactivo 25

¿Qué figura no corresponde al siguiente sólido?

1. 
2. 
3. 
4. 

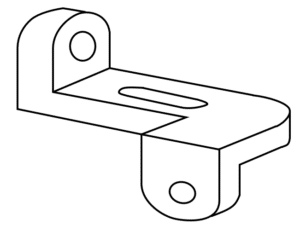
Solución:

Este problema se puede resolver muy rápido si observamos un detalle de la pieza tridimensional. Veamos que las dos pestañas están dobladas perpendicularmente respecto al cuerpo de la pieza.

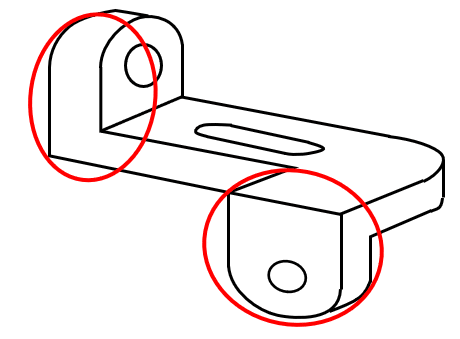
El inciso c) muestra una configuración en la que una de las pestañas no está plegada. Concluimos que el inciso c) no es una configuración de la pieza.

Reactivo 26

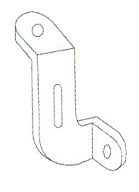
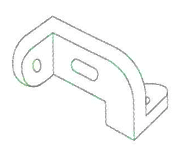
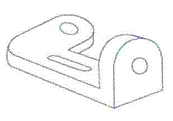
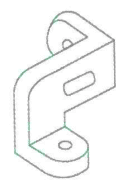
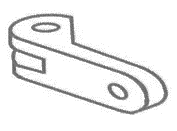
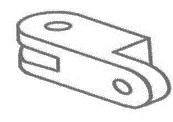
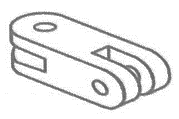
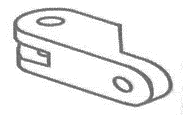
Identificar la figura que tiene las siguientes vistas:

1. 
2. 
3. 
4. 

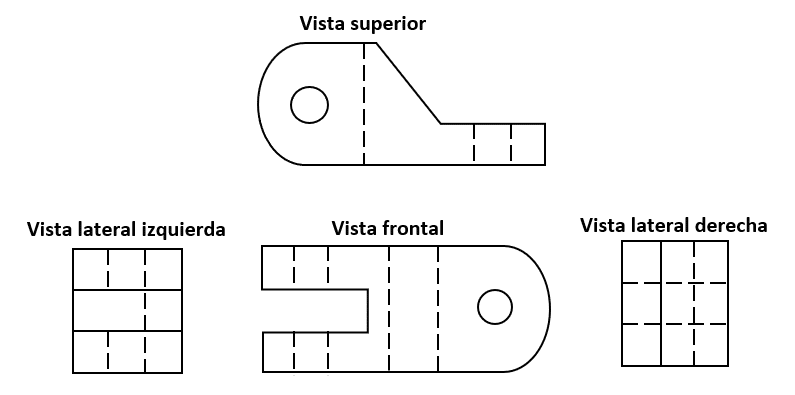
Solución:

A partir de la vista superior de la pieza tridimensional podemos descartar a los incisos b y c, ya que la forma que estas proyectan en el plano superior es distinta a la que muestra el enunciado.

El inciso d tiene más alargada la distancia entre el orificio y el inicio de la sección en diagonal, por lo tanto, esta representación corresponde con la vista superior dada. La pieza del inciso a no tiene la reparación antes mencionada, por ello la descartamos.

Con este sencillo análisis, concluimos que la respuesta correcta es el inciso d).

Reactivo 27

Identificar la figura que se obtiene al realizar los dobleces y cortes señalados en la hoja:

1. 
2. 
3. 
4. 

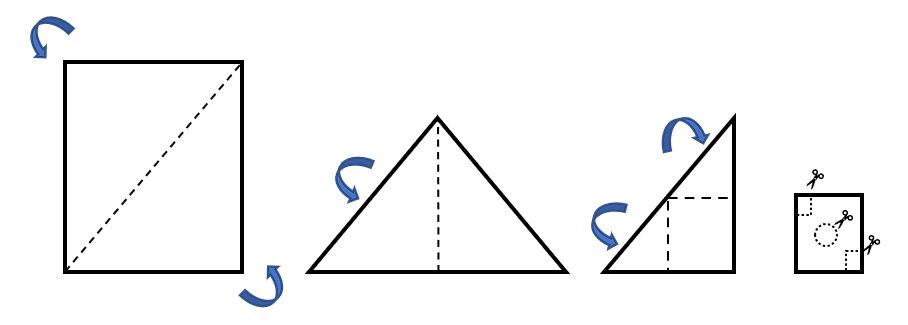
Solución:

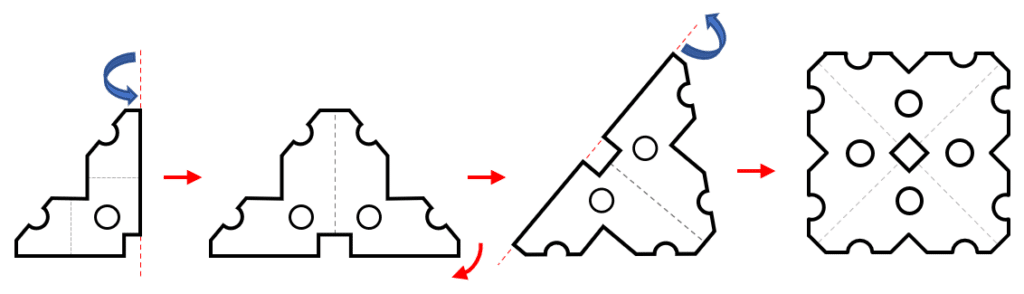
Para resolver el problema, puedes ayudarte de una hoja de papel cuadrada y unas tijeras. Debido a que la intención de la solución es que analices y entiendas los pasos para resolver un problema, vamos a examinar la disposición que deberán tener los recortes en la hoja desdoblada.

Señalemos como quedarían dispuestas las pestañas triangulares sobre el doblez final.

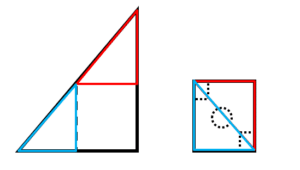
Al hacer los cortes sobre la figura 4 y desdoblar las pestañas triangulares, los recortes quedarán:

Desdoblamos el recorte para llegar a la segunda figura del enunciado.

Comparando con los incisos, concluimos que la respuesta correcta es el inciso c).

Reactivo 28

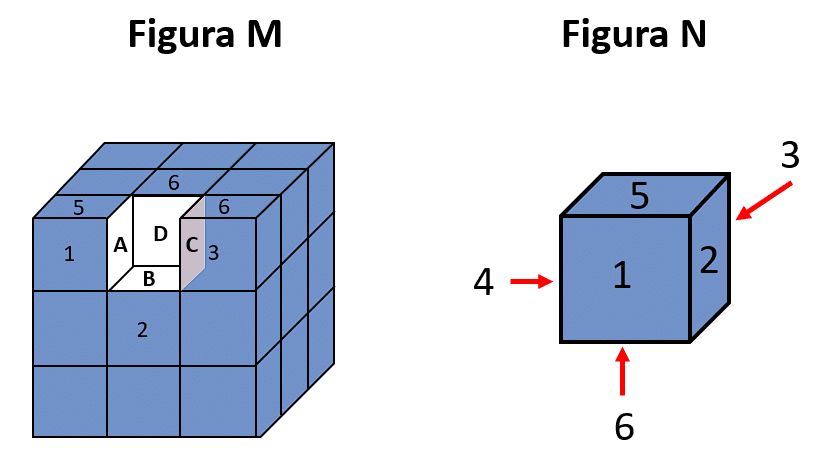
Las caras de cada uno de los cubos que integran la Figura M están numeradas como se ejemplifica en la Figura N, de tal modo que cada cara tiene el mismo número que su adyacente.

¿Qué valores corresponden a A, B, C y D , en ese orden, si estos resuelven la relación A+B+C+D=13 ?

1. 4, 5, 3, 1
2. 2, 4, 6, 1
3. 4, 3, 5, 1
4. 2, 6, 4, 1

Solución:

Teniendo en cuenta lo que establece el enunciado, podemos suponer que los cubos que conforman a la figura M son dados y la forma en la que se ordenan los números en las caras del “dado” se indica en la figura N.

Por ejemplo, el cubo de la esquina superior izquierda tiene dispuestas las caras 1 y 5 con la misma orientación que la figura N, esto significa que el valor de A es 2.

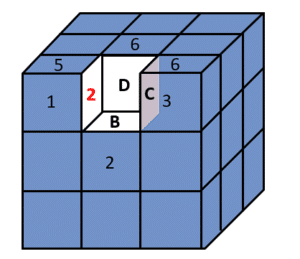
El mismo razonamiento podemos aplicar con el cubo de la esquina superior derecha. Para que la cara 6 quede en la parte superior, debemos rotar el cubo de la figura N respecto a la flecha que apunta al 4.

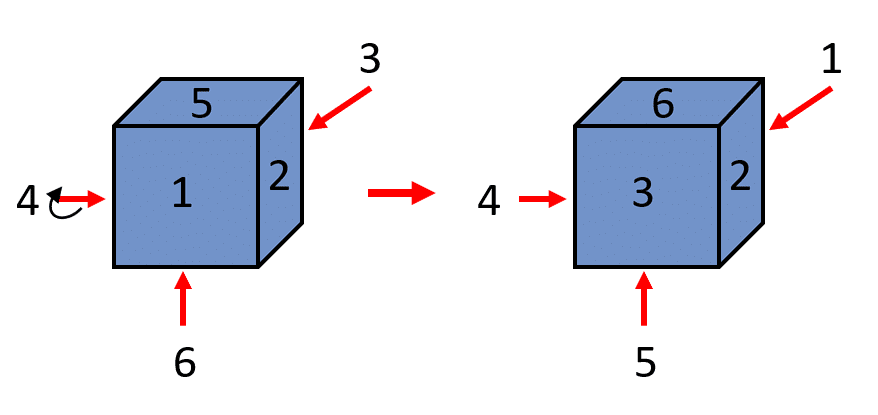
El valor de C es 4. Hasta este punto sabemos: 2, B, 4, D.

El único inciso con estos valores de A y C es el d). Concluimos el problema indicando al inciso d) como la respuesta correcta.

Reactivo 29

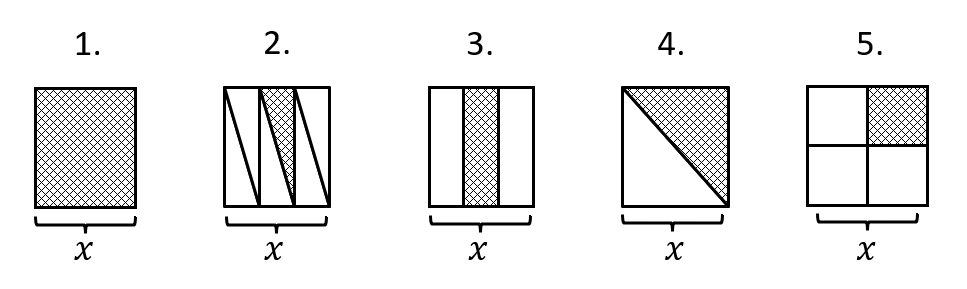
Ordenar de mayor a menor las siguientes figuras, considerando las áreas sombreadas.

1. 2, 4, 5, 3, 1
2. 1, 3, 2, 5, 4
3. 1, 4, 3, 5, 2
4. 2, 5, 3, 4, 1

Solución:

De forma casi evidente, la figura 1 es la que tiene el área sombreada mayor. Ahora, la siguiente con mayor área es la 4, porque la región sombreada equivale a la mitad del área del cuadrado. Con estas dos respuestas parciales: 1, 4, … podemos concluir que la respuesta correcta es el inciso c).

Si continuamos con este razonamiento, el área sombreada de la figura 3 es igual a \left(x\right)\left(\frac{x}{3}\right)=\frac{{x}^{2}}{3} , sería la siguiente mayor. El área de la figura 5 equivale a un cuarto del área total sería la penúltima menor y por descarte, la figura con menor área sombreada es la 2.

Reactivo 30

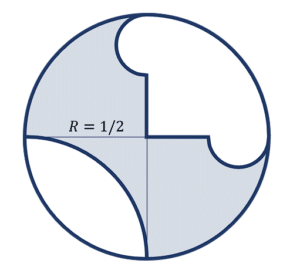
Calcular el área sombreada en la figura que se delimita por una circunferencia con diámetro de 1u.

1. \frac{3\pi }{4} {u}^{2}
2. \left(\frac{3\pi }{16}+1\right){u}^{2}
3. \frac{1}{4}\left(\frac{3\pi }{16}+1\right){u}^{2}
4. \frac{1}{16}\left(\frac{3\pi }{4}-1\right){u}^{2}

Solución:

Para calcular el área sombreada, primero debemos obtener el área de las figuras en color blanco para luego restarle el total al círculo de radio R=1/2 . A su vez, las figuras blancas se pueden separar de la siguiente forma:

{A}_{s}=\pi {\left(\frac{1}{2}\right)}^{2}-{A}_{B}=\frac{\pi }{4}-{A}_{B}

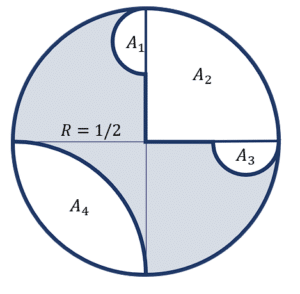
Tanto el área 1 como el área 3 son iguales y corresponden al área de media circunferencia de radio {r}_{2}=\frac{1}{8} . Por otra parte, el área {A}_{2} es igual a un cuarto de circunferencia de radio {r}_{1}=1/2 .

{A}_{1}={A}_{3}=\frac{\pi {\left(\frac{1}{8}\right)}^{2}}{2}=\frac{\pi }{128}

{A}_{2}=\frac{\pi {\left(\frac{1}{2}\right)}^{2}}{4}=\frac{\pi }{16}

Ahora, la figura 4 corresponde a un pétalo y el cálculo de su área es más complejo. Un pétalo se descompone de la siguiente forma:

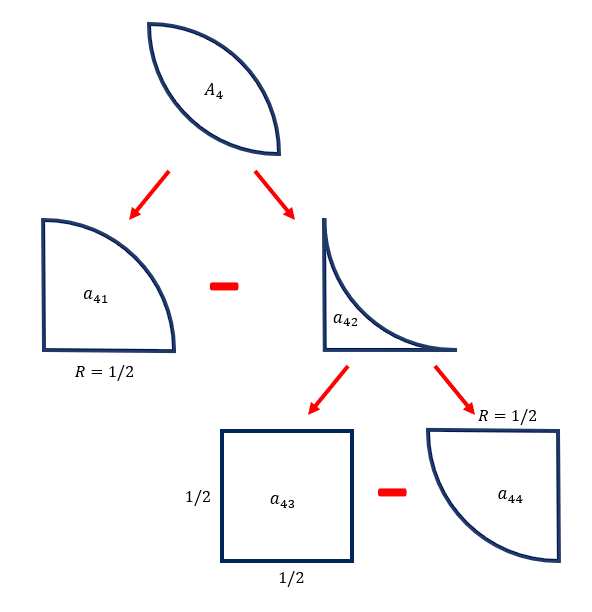
Esta es una de las dos formas en las que se puede descomponer el área de un pétalo. Tómate el tiempo que necesites para analizar la figura. Teniendo en cuenta la descomposición, podemos calcular el área {A}_{4} como:

{A}_{4}={a}_{41}-\left({a}_{43}-{a}_{44}\right)={a}_{41}-{a}_{43}+{a}_{44}

El área {a}_{44} es igual a {a}_{41} , ambas son el área de un cuarto de circunferencia.

{A}_{4}=2{a}_{414}-{a}_{43}

Tenemos que:

{a}_{414}=\frac{\pi {\left(\frac{1}{2}\right)}^{2}}{4}=\frac{\pi }{16}

{a}_{43}={\left(\frac{1}{4}\right)}^{2}=\frac{1}{16}

{A}_{4}=2\left(\frac{\pi }{16}\right)-\frac{1}{16}=\frac{\pi }{8}-\frac{1}{16}

Finalmente, el área blanca se calcula como:

{A}_{B}={A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}=\frac{\pi }{128}+\frac{\pi }{16}+\frac{\pi }{128}+\frac{\pi }{8}-\frac{1}{16}

Simplificando.

{A}_{B}=\frac{13\pi }{64}-\frac{1}{16}

Calculamos el área sombreada.

{A}_{s}=\frac{\pi }{4}-\left(\frac{13\pi }{64}-\frac{1}{16}\right)=\frac{\pi }{4}-\frac{13\pi }{64}+\frac{1}{16}=\frac{3\pi }{64}+\frac{1}{16}

Finalmente, extraemos \frac{1}{16} factor común:

{A}_{s}=\frac{1}{16}\left(\frac{3\pi }{4}+1\right)\mathrm{ }{\mathrm{u}}^{2}

Concluimos el problema indicando como respuesta correcta al inciso c).