¿No sabes como resolver los reactivos de física del IPN? Con este post iniciamos la solución de los 25 reactivos de física de la guía de estudio IPN 2023 para el área de Ciencias Sociales y Administrativas.
Por motivos de aprendizaje hemos dividido la guía en dos partes. De esta manera, asimilarás mejor el conocimiento, sobre todo en materias complejas como física. Inicia con la solución guiada de los reactivos que van desde el 1 al 10.
A continuación, tienes un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
¡Hay nuevas materias y la prueba tiene 140 preguntas! Continúa leyendo y entérate de lo nuevo.
Conoce el curso que cubre todos los temas del nuevo examen de ingreso al IPN con clases en vivo y exámenes simulacro.
Estructura del Examen IPN
La estructura del examen al IPN 2023 ha sido modificada. El total de reactivos por materia cambia en función al área de conocimientos. Las carreras del Instituto Politécnico Nacional se dividen en 3 grandes áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
Una pregunta común entre los aspirantes al IPN es: ¿qué tan difícil es entrar al IPN? La respuesta depende de un único factor: las horas de estudio que inviertas en tu preparación para el examen.
En la convocatoria se incluyen 2 nuevas asignaturas: historia e inglés (reading comprehension), por lo que el número de reactivos incremetó a 140. La guía de física para el área de Ciencias Sociales y Administrativas, incluyen reactivos de física I del nivel medio superior.
Conoce todo acerca de la convocatoria IPN 2023
Temario de física del área CySA IPN 2023
Estos son los temas de física que deberás estudiar antes de presentar el examen:
| Tema | Rama |
|---|---|
| Introducción a la física | CSyA |
| Cinemática | IyCFM, CSyA |
| Estática | IyCFM, CMB, CSyA |
| Dinámica | CSyA |
| Propiedades de la materia | IyCFM, CSyA |
| Calor y temperatura | CSyA |
| Electricidad y magnetismo | CSyA |
| Ondas | IyCFM, CSyA |
¿Cómo resolver la guía del IPN 2023?
Revisa la bibliografía recomendada en la guía de estudio antes de iniciar con los reactivos. Un error común entre los aspirantes es estudiar la teoría mientras resuelven la guía.
Es normal querer ir rápido para terminar la guía lo más pronto posible, pero rapidez rara vez implica calidad. El proceso de aprendizaje necesita tiempo, que reflexiones acerca de los temas y que los comprendas desde tu punto de vista.
Los siguientes consejos te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
- Física no se trata de aplicar fórmulas. Debes conocer los fundamentos, analizar los enunciados y seleccionar las leyes correctas para resolver el problema.
Reactivo 1
Seleccionar la opción que representa una cantidad vectorial.
- 45 °C
- -45 kg
- 290 N, 145°
- 350 kg, 140°
Solución:
Las cantidades vectoriales son aquellas que especifican magnitud, dirección y sentido. Son cantidades que indican información extra acerca de la magnitud física que representan, respecto a las escalares, que solo expresan un valor numérico.
Un ejemplo clásico de magnitud vectorial es la fuerza. El vector fuerza describe la magnitud de la fuerza, pero también la dirección y el sentido en el que se aplica. Teniendo en cuenta esta información, podemos descartar a los incisos a) y b).
Por otro lado, entre el inciso c) y el d), descartamos al inciso d) porque la masa no es una magnitud vectorial. La masa representa la cantidad de materia que compone a un cuerpo y no tiene asociada una dirección o sentido.
Concluimos que la respuesta correcta es el inciso c), que representa a una fuerza de 290 Newtons aplicada en la dirección de 145°.
Reactivo 2
¿Qué distancia recorre una moto en 4 horas si su velocidad es de 90 km/h?
- 60 km
- 90 km
- 150 km
- 360 km
Solución:
El enunciado nos indica el intervalo de tiempo y la rapidez de la moto. Solo debemos multiplicar el intervalo de tiempo por la rapidez para obtener la distancia recorrida.
\mathrm{\Delta }x=90\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot 4 \mathrm{h}=360\mathrm{ }\mathrm{k}\mathrm{m}
La moto ha recorrido 360 kilómetros.
Indicamos como respuesta correcta al inciso d).
Reactivo 3
¿Cuál es la rapidez media de un coche que recorre 80 km en 90 minutos?
- 40 km/h
- 60 km/h
- 140 km/h
- 160 km/h
Solución:
Debemos transformar el intervalo de tiempo a horas.
90 \mathrm{m}\mathrm{i}\mathrm{n}\cdot \frac{1 \mathrm{h}}{60 \mathrm{m}\mathrm{i}\mathrm{n}}=1.5 \mathrm{h}
Ahora, calculamos la rapidez dividiendo a la distancia recorrida por el intervalo de tiempo.
v=\frac{80 \mathrm{k}\mathrm{m}}{1.5 \mathrm{h}}=53.3\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}
La respuesta correcta no se encuentra entre los incisos. La guía establece que es el b) pero este no indica el valor que hemos calculado. Hay un error en este reactivo.
Reactivo 4
La _______ promedio de una partícula está definida como el desplazamiento de la partícula dividido entre el intervalo de tiempo.
- rapidez
- distancia
- velocidad
- aceleración
Solución:
Para seleccionar la respuesta correcta, debemos tener claras las definiciones de rapidez y velocidad. La rapidez es una magnitud escalar que representa el cociente entre la distancia recorrida y el intervalo de tiempo en el que se ha efectuado.
Por otra parte, la velocidad es una magnitud vectorial representada por el cociente entre el vector desplazamiento y el intervalo de tiempo en el que se ha efectuado.
Teniendo en cuenta estas definiciones y considerando el resto de la frase, concluimos que el enunciado hace referencia a la velocidad promedio.
La velocidad promedio de una partícula está definida como el desplazamiento de la partícula dividido entre el intervalo de tiempo.
Concluimos el problema indicando como respuesta correcta al inciso c).
Reactivo 5
¿Qué gráficas representan el movimiento a velocidad constante?
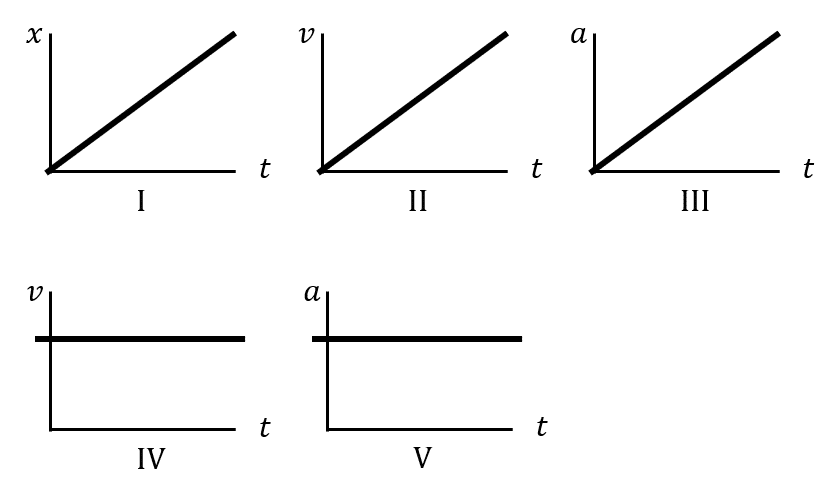
- IV y V
- I, ll y lll
- l y ll
- l y lV
Solución:
A partir de las relaciones integro – diferenciales entre la posición, la velocidad y la aceleración, sabemos que la velocidad constante se obtiene al derivar a la posición en función del tiempo representada por una línea recta oblicua.
x\left(t\right)=\pm mt+b\to v\left(t\right)=\frac{dx\left(t\right)}{dt}
\frac{d\left(\pm mt+b\right)}{dt}=\pm m
En términos gráficos, la velocidad constante se dibuja como una línea horizontal. Teniendo en cuenta lo anterior, las gráficas que muestran a la posición como una línea oblicua y a la velocidad como una línea horizontal son: I y IV.
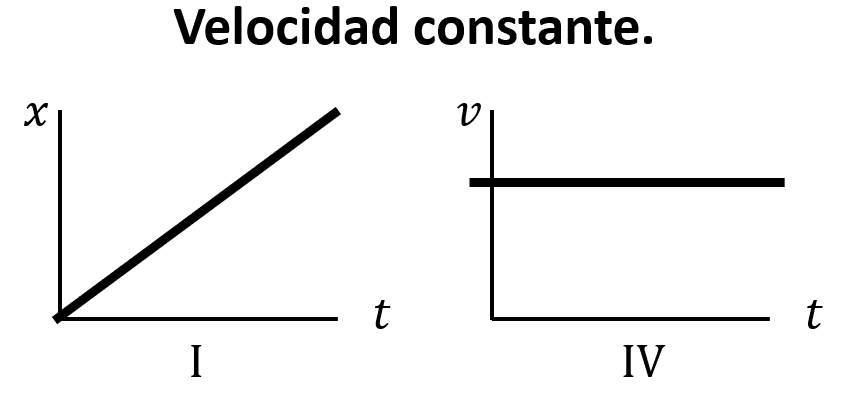
La respuesta correcta es el inciso d).
Reactivo 6
Un automóvil mantiene una aceleración constante de 9\frac{\mathrm{m}}{{\mathrm{s}}^{2}} . Si su velocidad inicial fue de 40\frac{\mathrm{m}}{\mathrm{s}} al norte, ¿cuál será su velocidad después de 7 s?
- 25\frac{\mathrm{m}}{\mathrm{s}}
- 48\frac{\mathrm{m}}{\mathrm{s}}
- 103\frac{\mathrm{m}}{\mathrm{s}}
- 143\frac{\mathrm{m}}{\mathrm{s}}
Solución:
El enunciado nos indica que la velocidad inicial del automóvil es hacia el norte, es decir, positiva. Para el cálculo, utilizamos las ecuaciones de cinemática para el MRUA.
{v}_{f}={v}_{o}+at
Sustituimos.
{v}_{f}=40+\left(9\right)\left(7\right)=103 \mathrm{m}/\mathrm{s}
La velocidad una vez han transcurrido 7 segundos es de 103 m/s. La respuesta correcta es el inciso c).
Reactivo 7
Un joven comienza a caminar de su casa a la escuela, que se encuentra hacia el sur, y tarda media hora en llegar. Durante su recorrido alcanza una aceleración de 0.002 \mathrm{m}/{\mathrm{s}}^{2} . Al llegar a la escuela la encuentra cerrada por lo que regresa a su casa en la siguiente media hora. Calcular la distancia que recorrió el joven en los primeros 20 minutos.
- 112 m
- 225 m
- 1440 m
- 2810 m
Solución:
Para el cálculo, nos interesa la aceleración de 0.002 \mathrm{m}/{\mathrm{s}}^{2} . Además, consideramos que el joven parte del reposo: {v}_{o}=0 \mathrm{m}/\mathrm{s} . Debemos convertir los 20 minutos a segundos.
20 \mathrm{m}\mathrm{i}\mathrm{n}\cdot \frac{60 \mathrm{s}}{1 \mathrm{m}\mathrm{i}\mathrm{n}}=1200 \mathrm{s}
Empleamos la ecuación de posición en función del tiempo para el MRUA. En este caso en particular, no es necesario considerar el signo de la aceleración (negativo por ir hacia el sur) porque solo nos interesa la distancia recorrida.
{y}_{f}={y}_{o}+{v}_{o}t+\frac{a{t}^{2}}{2}
La posición inicial es {y}_{o}=0 , {v}_{o}=0 , a=0.002 \mathrm{m}/{\mathrm{s}}^{2} y t=1200 \mathrm{s} .
{y}_{f}=0+\left(0\right)\left(1200\right)+\frac{\left(0.002\right){\left(1200\right)}^{2}}{2}
\therefore {y}_{f}=1440 \mathrm{m}
El estudiante camina 1440 metros en los primeros 20 minutos.
Concluimos el problema indicando como respuesta correcta al inciso c).
Reactivo 8
Dos objetos de masas {m}_{1}=20 \mathrm{k}\mathrm{g} y {m}_{2}=40 \mathrm{k}\mathrm{g} , situados en una mesa horizontal, están unidos mediante una cuerda ligera. Se ejerce una fuerza F=90 \mathrm{N} hacia la derecha sobre uno de los objetos. Determinar la aceleración ( m/{s}^{2} ) del sistema.
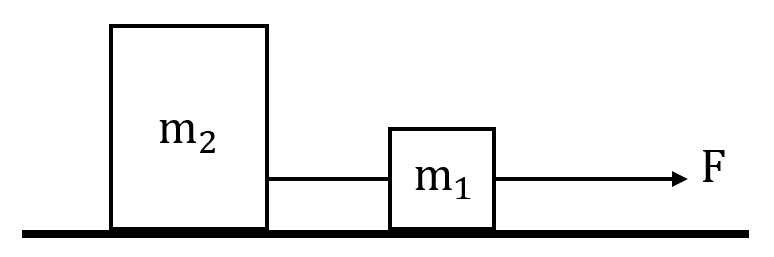
- 1.5
- 6.2
- 9.5
- 20.2
Solución:
En este caso no es necesario hacer el diagrama de cuerpo libre sobre las masas para identificar que la fuerza F actúa por igual sobre ambas masas, debido a que la misma se transfiere a la masa 2 por la tensión de la cuerda al aplicar la tercera ley de Newton.
Lo anterior significa que podemos estudiar al sistema como una sola masa m={m}_{1}+{m}_{2} .
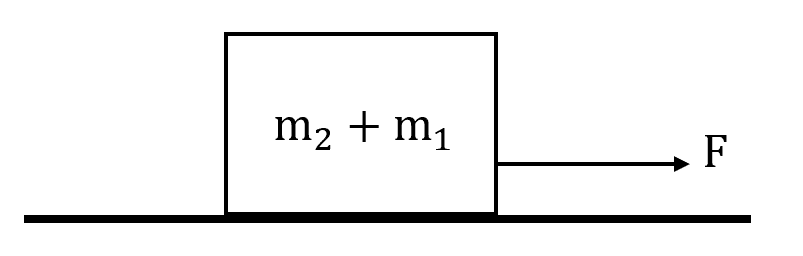
Ahora, para el cálculo de la aceleración empleamos la segunda Ley de Newton.
F=\left({m}_{1}+{m}_{2}\right)a
La ecuación anterior representa el módulo de los vectores involucrados.
a=\frac{F}{{m}_{1}+{m}_{2}}
Sustituimos:
a=\frac{90}{20+40}=1.5 \mathrm{m}/{\mathrm{s}}^{2}
La respuesta correcta al problema es el inciso a).
Reactivo 9
Calcular la aceleración (en \mathrm{m}/{\mathrm{s}}^{2} ) de un objeto que pasa de 36 km/h a 20 km/h en 8 segundos.
- 10.14\mathrm{m}/{\mathrm{s}}^{2}
- 5.0\mathrm{m}/{\mathrm{s}}^{2}
- -0.55\mathrm{m}/{\mathrm{s}}^{2}
- -5.0\mathrm{m}/{\mathrm{s}}^{2}
Solución:
Calculamos la aceleración media mediante la siguiente ecuación:
{a}_{m}=\frac{{v}_{2}-{v}_{1}}{\mathrm{\Delta }t}
Convertimos las velocidades a metros por segundo.
36\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}\cdot \frac{1000 \mathrm{m}}{1 \mathrm{k}\mathrm{m}}=10 \mathrm{m}/\mathrm{s}
20\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}\cdot \frac{1000 \mathrm{m}}{1 \mathrm{k}\mathrm{m}}=5.55 \mathrm{m}/\mathrm{s}
Sustituimos en la ecuación:
{a}_{m}=\frac{5.55-10}{8}=-0.55 \mathrm{m}/{\mathrm{s}}^{2}
La aceleración del objeto es de -0.55 \mathrm{m}/{\mathrm{s}}^{2} .
La respuesta correcta es el inciso c).
Reactivo 10
Un objeto de 2 kg se deja caer libremente de un avión que vuela a 2 km de altura. Determinar la velocidad con la que llegará al suelo. Considerar g=10\mathrm{m}/{\mathrm{s}}^{2} .
- 19\mathrm{m}/\mathrm{s}
- 62\mathrm{m}/\mathrm{s}
- 200\mathrm{m}/\mathrm{s}
- 400\mathrm{m}/\mathrm{s}
Solución:
Para resolver el problema, empleamos la ecuación de velocidad para la caída libre de los cuerpos.
{v}_{f}^{2}=-2g\left({y}_{f}-{y}_{o}\right)
Convertimos a la posición inicial de kilómetros a metros.
2 \mathrm{k}\mathrm{m}\cdot \frac{1000 \mathrm{m}}{1 \mathrm{k}\mathrm{m}}=2000 \mathrm{m}
Sustituimos en la ecuación: {y}_{o}=2000 \mathrm{m} , {y}_{f}=0 \mathrm{m} y g=10 \mathrm{m}/{\mathrm{s}}^{2} .
{v}_{f}=\sqrt{2\left(10\right)\left(2000-0\right)}=200 \mathrm{m}/\mathrm{s}
La velocidad del objeto es igual a 200 metros por segundo.
Examinando a los incisos, concluimos indicando como respuesta correcta al c)
