Resolvemos la segunda y última parte de la guía interactiva del EXANI II resuelta, correspondiente al módulo Física desde el reactivo 13 hasta el 24.

Recuerda que puedes continuar estudiando todo el contenido para el examen con los materiales gratuitos de EXANI II.
Reactivo 13
Un futbolista patea una pelota de 0.420 kg que se encuentra en reposo. La pelota avanza con una velocidad de 19 m/s.
Considerando que el tiempo de contacto entre el pie y el balón dura 0.8 segundos, calcule la fuerza que se ejerce sobre el balón.
- 6.384 N
- 9.975 N
- 56.548 N
Solución:
Para resolver este problema, se utiliza la fórmula del impulso:
I=F\cdot \mathrm{\Delta }t
Por otro lado, el impulso es también igual a la variación del momento lineal:
I=\mathrm{\Delta }p={p}_{2}-{p}_{1}
Sustituyendo en la ecuación del impulso:
{p}_{2}-{p}_{1}=F\cdot \mathrm{\Delta }t
Despejando la magnitud de la fuerza:
F=\frac{{p}_{2}-{p}_{1}}{\mathrm{\Delta }t}
Prescindimos de la notación vectorial, porque las cantidades son unidimensionales. Esto se puede hacer siempre que respetemos el signo de las cantidades. La velocidad inicial de la pelota es {v}_{1}=0 mientras que luego de ser pateada vale {v}_{2}=19 \mathrm{m}/\mathrm{s} .
Si la cantidad de movimiento es mv nos queda:
F=\frac{m{v}_{2}-m\left(0\right)}{\mathrm{\Delta }t}=\frac{m{v}_{2}}{\mathrm{\Delta }t}
Sustituimos los valores:
F=\frac{\left(0.42\right)\left(19\right)}{0.8}=9.975 \mathrm{N}
La fuerza promedio que experimenta la pelota durante el contacto es de 9.975 \mathrm{N} .
La respuesta correcta es el inciso b). En el inciso a) se utiliza la fórmula correcta para el momento lineal, pero se despeja de forma incorrecta la fuerza de la ecuación del impulso, quedando F=m {v}_{2}\mathrm{\Delta }t .
El error de la opción c) es que se ha dividido la velocidad en el segundo instante por el producto de la masa y el intervalo de tiempo en que se aplica la fuerza \frac{{v}_{2}}{m\mathrm{\Delta }t} . Este procedimiento también es incorrecto.
Reactivo 14
Identifique en la imagen el número que corresponde al nodo.
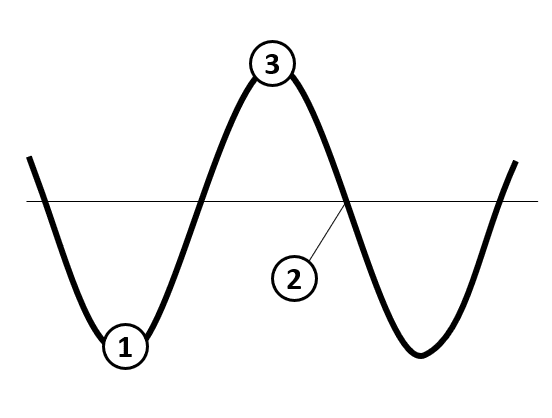
- 1
- 2
- 3
Solución:
Los nodos, son puntos de una onda estacionaria cuya amplitud no varía en el tiempo, normalmente se mantiene paralela al punto de equilibrio. Un ejemplo de nodo son los extremos de una cuerda de guitarra, estos puntos nunca se desplazan.
A partir de la imagen, podemos identificar fácilmente que el nodo está señalado con el número 2. Por lo tanto, la respuesta correcta es el inciso b). La opción a) es incorrecta, porque esta corresponde con un valle de la onda, mientras que el punto 3 con una cresta.
Reactivo 15
Las partículas de una onda mecánica transversal vibran _______ a la dirección de la propagación.
- paralelamente
- perpendicularmente
- oblicuamente
Solución:
Las ondas transversales son aquellas que oscilan perpendicularmente a la dirección de propagación. Las ondas en una cuerda son un ejemplo clásico de ondas mecánicas transversales.
Este tipo de ondas provocan que las partículas del medio por el que se propagan oscilan perpendicularmente a la dirección de propagación. Teniendo en cuenta todo lo anterior, concluimos que la respuesta correcta es el inciso b).
Las ondas que oscilan paralelamente a la dirección de propagación se denominan longitudinales. Por otra parte, lo dicho en el inciso c) carece de sentido y no es una clasificación válida de las oscilaciones mecánicas.
Reactivo 16
Se desea apretar una tuerca que se encuentra floja. Para que exista un torque máximo, la manera de agarrar la llave es…
- lo más cerca posible de la cabeza de la llave
- exactamente a la mitad de la llave
- lo más alejado posible de la cabeza de la llave
Solución:
En su forma más rigurosa, el torque se calcula como el producto vectorial entre el vector fuerza y el vector radio de acción.
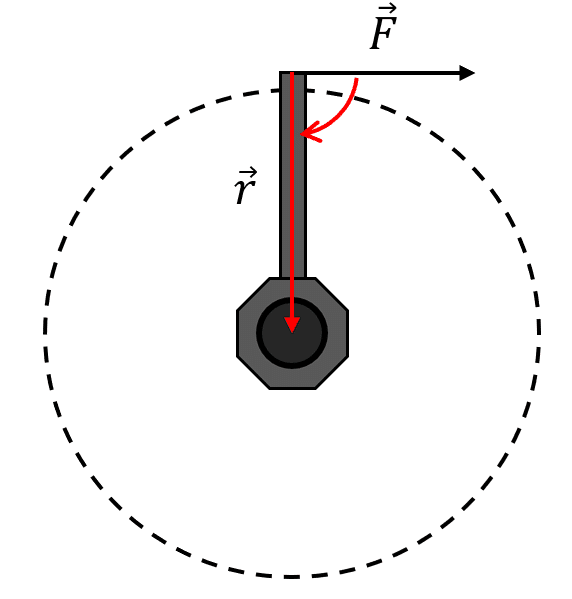
\overrightarrow{\tau }=\overrightarrow{F}\times \overrightarrow{r}
La magnitud del torque se obtiene como:
\tau =F\cdot r\cdot \mathrm{sin}{\angle }_{r}^{F}
Donde {\angle }_{r}^{F} es el menor ángulo entre la fuerza y el vector radio. Suponiendo que {\angle }_{r}^{F}=90° , provocando que el seno valga 1, solo nos queda un parámetro para variar: el radio de acción. Mientras más alejado apliquemos la fuerza, mayor será la magnitud del torque.
Teniendo en cuenta lo anterior, la respuesta correcta es el inciso c).
Se desea apretar una tuerca que se encuentra floja. Para que exista un torque máximo, la manera de agarrar la llave es lo más alejado posible de la cabeza de la llave.
En el inciso a), se tendría el mínimo torque posible y sería necesario aplicar mucha fuerza. Por otro lado, aplicado a la mitad como dice el inciso b) sólo obtendremos la mitad del torque posible.
Reactivo 17
Para medir la velocidad del viento se construye un aparato de 3 copas, como el que se muestra en la imagen. Si cada copa tiene una masa de 0.2 kg y las varillas, de masa despreciable, tienen una longitud de 0.5 m, ¿cuál es el momento de inercia cuando el sistema rota?
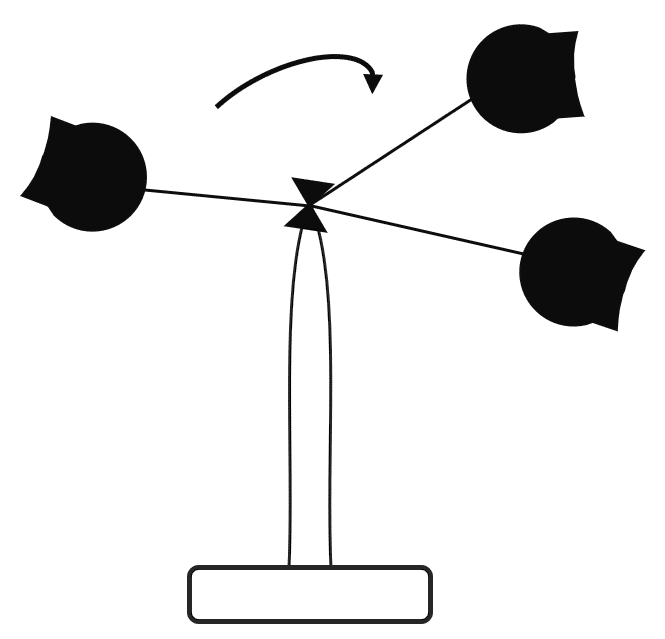
- 0.05 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2}
- 0.10 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2}
- 0.15 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2}
Solución:
Primero, debemos considerar al sistema de las tres copas como un sistema de tres partículas de masa m=0.2 \mathrm{k}\mathrm{g} y que distan r=0.5 \mathrm{m} del eje de giro. Por lo tanto, el momento de inercia del sistema de partículas es igual a la suma del momento de inercia de cada copa.
I={I}_{1}+{I}_{2}+{I}_{3}
Recordemos que el momento de inercia de una partícula se calcula como el producto de la masa por el radio al cuadrado.
I=m{r}^{2}+m{r}^{2}+m{r}^{2}=3m{r}^{2}
Sustituyendo:
I=3\left(0.2\right){\left(0.5\right)}^{2}=0.15 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2}
La respuesta correcta es el inciso c). En el inciso a) se calcula la inercia rotacional de una sola copa, mientras que en el b) se cometen dos errores: no se eleva al cuadrado el radio y solo se considera una copa.
Reactivo 18
Se coloca un imán dentro de una caja de cartón cuyas caras tienen un área de 0.01 {\mathrm{m}}^{2} cada una. Si la densidad de flujo magnético es B=2\times {10}^{-1} \mathrm{T} , ¿qué cantidad de líneas de carga atraviesan la tapa?
- 2\times {10}^{-3} \mathrm{W}\mathrm{b}
- 2\times {10}^{1} \mathrm{W}\mathrm{b}
- 5\times {10}^{-2} \mathrm{W}\mathrm{b}
Solución:
En este caso, se nos pide calcular el flujo magnético que atraviesa a una de las caras de la caja. La ecuación del flujo magnético es:
\varphi =B\cdot A
Sustituimos la magnitud del campo y el área:
\varphi =\left(2\times {10}^{-1}\right)\left(0.01\right)=2\times {10}^{-3} \mathrm{W}\mathrm{b}
Las unidades del flujo magnético son el Weber \left[Wb\right] .
La respuesta correcta es el inciso a). En la opción b) se calcula el cociente entre la intensidad de campo y el área, mientras que en el c) el cociente del área y la intensidad de campo. Ambos procedimientos incorrectos.
Reactivo 19
Una masa de 90 kg se desliza 30° hacia abajo sobre un plano inclinado.
¿Cuál es el valor necesario de la fuerza de fricción para que la masa se mueva a una velocidad constante?
Considere: g=10\frac{\mathrm{m}}{{\mathrm{s}}^{2}},\mathrm{sin}30°=0.5,\mathrm{cos}30°=0.87 y \mathrm{tan}30°=0.85 .
- 450 N
- 783 N
- 900 N
Solución:
Primero, realizamos una representación gráfica de la situación planteada.
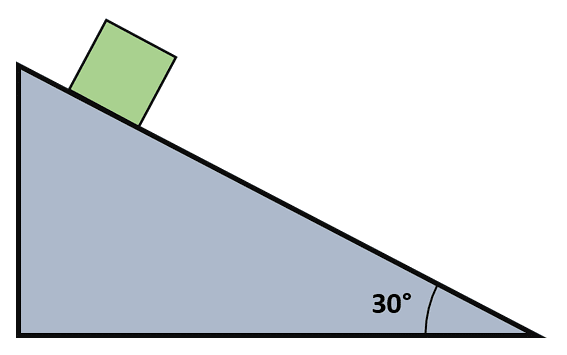
La fricción es una fuerza que se opone al movimiento de un cuerpo y que aparece cuando las superficies no son perfectamente lisas. Si la masa se desliza hacia abajo por el plano inclinado, entonces la fuerza de fricción apunta en sentido contrario.
Ahora, realizamos un diagrama de cuerpo libre para descomponer las fuerzas sobre la masa.
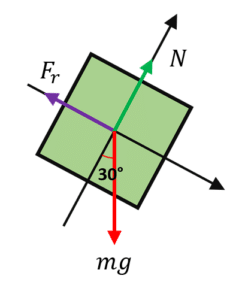
Debido a que el plano es inclinado, el peso queda a 30 grados del eje vertical trazado en el centro de la masa. Además, la fuerza de fricción sería la que se opone a la componente horizontal del peso.
Debido a que solo nos interesa la magnitud de la fuerza de roce, descomponemos las fuerzas sobre el eje x únicamente. Aplicamos la primera ley de Newton, porque nos interesa que la masa permanezca estática.
\sum {F}_{x}:mg\mathrm{sin}30-Fr=0
Despejando la magnitud de la fuerza de roce obtenemos:
{F}_{r}=mg\mathrm{sin}30
Sustituyendo los valores correspondientes:
{F}_{r}=\left(90\right)\left(10\right)\left(0.5\right)=450 \mathrm{N}
Para que el bloque no se deslice por la rampa inclinada, la fuerza de roce debe ser igual a 450 N.
La respuesta correcta es el inciso a). En la opción b) se considera incorrectamente que la fricción es la componente horizontal del peso y se ha calculado:
{F}_{r}=\left(90\right)\left(10\right)\mathrm{cos}30°
Por otro lado, en la respuesta c) no se ha considerado que el plano sobre el que se encuentra la masa está inclinado 30°.
Reactivo 20
Una persona y su moto, juntas, constituyen una masa de 300 kg. Si el conductor toma una curva con radio de 20 \mathrm{m} a una velocidad de 10\frac{\mathrm{m}}{\mathrm{s}} , ¿cuál es la fuerza centrípeta necesaria para que la moto consiga mantenerse en dicha curva?
- 150 N
- 1 500 N
- 3 000 N
Solución:
La fuerza centrípeta es aquella que tira a los cuerpos en movimiento circular uniforme hacia el centro. La fórmula para calcular la magnitud de la fuerza centrípeta es:
{F}_{c}=\frac{m{v}^{2}}{r}
Sustituimos en la ecuación:
{F}_{c}=\frac{\left(300\right){\left(10\right)}^{2}}{20}=1500 \mathrm{N}
La fuerza centrípeta que experimenta la persona y su moto es de 1500 Newtons.
La respuesta correcta es el inciso b). En el inciso a) no se ha elevado al cuadrado la velocidad tangencial, mientras que en el c) se ha utilizado la segunda ley de Newton, pero sustituyendo a la aceleración por la fuerza, esto es un error conceptual.
Reactivo 21
¿Cuál es la longitud de un péndulo que oscila con una frecuencia de 2.1 Hz?
Considere \pi =3.14 y g=10 \mathrm{m}/{\mathrm{s}}^{2} .
- 05 m
- 12 m
- 36 m
Solución:
La frecuencia de oscilación de un péndulo simple se calcula como:
f=\frac{1}{2\pi }\sqrt{\frac{g}{l}}
Donde g es la aceleración de la gravedad y l la longitud del péndulo. Despejamos la longitud:
l=\frac{g}{{\left(2\pi f\right)}^{2}}
Sustituimos:
l=\frac{10}{{\left(2\pi \cdot 2.1\right)}^{2}}=0.05 \mathrm{m}
La longitud del péndulo es igual a 0.05 metros. La respuesta correcta es el inciso a). En el inciso b) no se ha elevado al cuadrado la frecuencia, mientras que en la c) solo se ha elevado al cuadrado la frecuencia.
Reactivo 22
Se tienen 2 masas unidas como se muestra en la figura. Si el sistema gira en torno al punto medio de la barra con una velocidad angular de 4\frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}} y la masa de la barra es despreciable, ¿cuál es el momento angular de las masas?
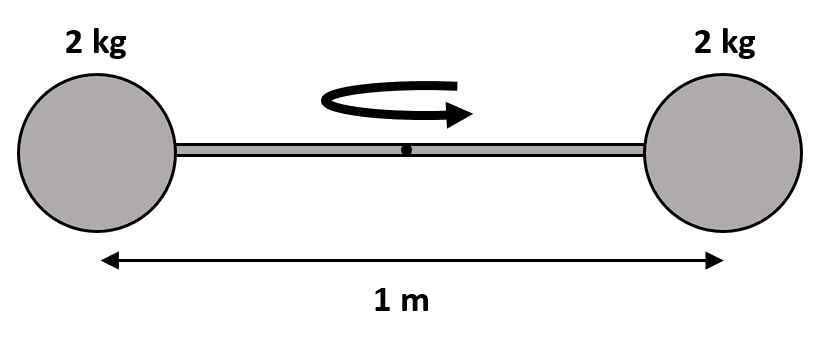
- 2 \mathrm{k}\mathrm{g}\cdot \frac{{\mathrm{m}}^{2}}{s}
- 4 \mathrm{k}\mathrm{g}\cdot \frac{{\mathrm{m}}^{2}}{s}
- 8 \mathrm{k}\mathrm{g}\cdot \frac{{\mathrm{m}}^{2}}{s}
Solución:
El momento angular del sistema se calcula como el producto de la inercia rotacional del sistema por su velocidad angular.
L=I\omega
La velocidad angular es un dato proporcionado por el enunciado, pero la inercia rotacional debe calcularse. Debido a que podemos tratar el ejercicio como un sistema de partículas, la inercia rotacional total se obtiene como:
I={I}_{1}+{I}_{2}=m{r}^{2}+m{r}^{2}
Tanto las masas como los radios son iguales, por lo tanto:
I=2m{r}^{2}
Sustituyendo:
L=2m{r}^{2}\omega
Evaluamos la ecuación. La distancia entre las masas es igual a 1, pero el radio es la mitad.
L=2\left(2\right){\left(0.5\right)}^{2}\left(4\right)=4 \mathrm{k}\mathrm{g}\frac{{\mathrm{m}}^{2}}{\mathrm{s}}
La respuesta correcta es el inciso b). En el inciso a) se calcula el momento de inercia para una sola masa, por ello se obtiene como resultado 2 \mathrm{k}\mathrm{g}\frac{{\mathrm{m}}^{2}}{\mathrm{s}} . Por otro lado, en el inciso c) no se ha elevado al cuadrado el radio en la fórmula de la inercia rotacional.
Reactivo 23
Determine el índice de refracción de una sustancia cuando la velocidad de la luz en ella es de 2.56\times {10}^{8} \mathrm{m}/\mathrm{s} . Considere la velocidad de la luz en el vacío c=3\times {10}^{8} \mathrm{m}/\mathrm{s} .
- 0.85
- 1.17
- 7.68
Solución:
El índice de refracción permite cuantificar el cambio de velocidad que sufre la luz al trasladarse por un medio distinto al vacío y se calcula como el cociente de la velocidad de la luz en el vacío y en el medio.
n=\frac{c}{v}
Sustituimos:
n=\frac{3\times {10}^{8}}{2.56\times {10}^{8}}=1.17
El índice de refracción de la luz en la sustancia es de 1.17.
La respuesta correcta es el inciso b). En el inciso a) se aplica la fórmula al revés, se divide la velocidad en el medio sobre la velocidad en el vacío.
Por otro lado, en la opción c) se multiplican las velocidades sin tener en cuenta el {10}^{8} , procedimiento totalmente incorrecto.
Reactivo 24
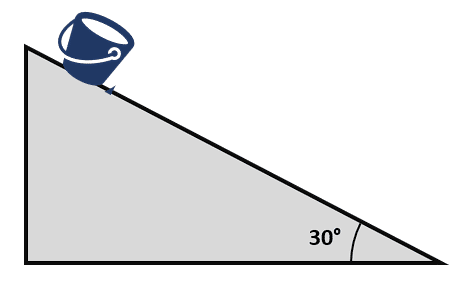
Se improvisó el montaje de una rampa metálica para bajar cubos de cemento de 10 kg por acción de la fuerza de gravedad. Si la inclinación de dicha rampa es de 30°, ¿cuál es la fuerza de fricción que logra que los cubos se deslicen a una aceleración constante?
Considere: g=10\frac{\mathrm{m}}{{\mathrm{s}}^{2}},\mathrm{sin}30°=0.5,\mathrm{cos}30°=0.87 y \mathrm{tan}30°=0.85 .
- 50 N
- 87 N
- 100 N
Solución:
A partir de las leyes de Newton, sabemos que la sumatoria de fuerzas externas sobre un cuerpo es igual a cero cuando: se encuentra detenido o se desplaza a velocidad constante. Por lo tanto, aplicamos sumatorias de fuerzas al cubo de cemento con la premisa de:
\sum F=0
Realizamos una representación gráfica de lo planteado por el enunciado.
Realizamos el diagrama de cuerpo libre del cubo.
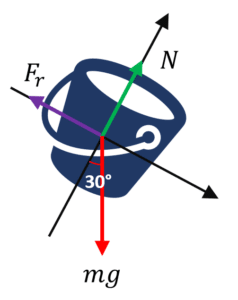
Debido a que el cubo se va a desplazar en la dirección horizontal de los ejes, aplicamos la descomposición de fuerzas en esta dirección para obtener la magnitud de la fuerza de roce.
\sum {F}_{x}:mg\mathrm{sin}30-{F}_{r}=0
Despejamos y evaluamos:
{F}_{r}=mg\mathrm{sin}30=\left(10\right)\left(10\right)\left(0.5\right)=50 \mathrm{N}
Para que el cubo se desplace a velocidad constante, la fuerza de roce debe ser igual a 50 Newtons. La respuesta correcta es el inciso a). En el inciso b) se ha descompuesto incorrectamente el peso, se utiliza el coseno en lugar del seno de 30°.
Por otro lado, en la opción c) se utiliza la segunda ley de Newton, pero esto es un error conceptual. Cuando un cuerpo se desplaza a velocidad constante, su aceleración es cero, por lo tanto m\cdot a=0 .

