¡Felicidades aspirante! Llegamos a la tercera y última parte del simulacro resuelto de Aritmética para la prueba de ingreso EXANI II. Vamos a la solución de los reactivos del 41 al 50.

Luego de culminar esta parte toma un descanso, haz alguna actividad que te relaje y luego repasa los procedimientos que seguiste. Esto te ayudará a meditar y afianzar los conocimientos que estas construyendo.
Ejercicios de Aritmética
Sin más preámbulos, pasamos a la última parte de este simulacro. Recuerda que en nuestra web puedes encontrar más simulacros como este, diseñados para que te conviertas en una o un crack de los temas que enfrentarás en la prueba de admisión.
Reactivo 41
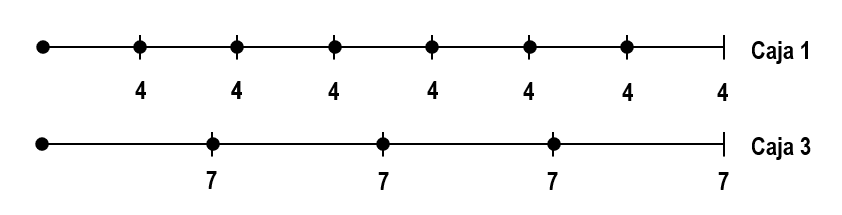
En un supermercado, el supervisor de caja se ha dado cuenta que por la caja 1 pasa un cliente cada 4 minutos y por la caja 3 pasa uno cada 7 minutos. Como parte de un estudio logístico, la empresa necesita saber cuánto tiempo debe transcurrir para que haya un cliente en ambas cajas.
- 27 min
- 8 min
- 49 min
Solución:
Este problema se resuelve aplicando el mínimo común múltiplo de los tiempos que tardan los clientes en cada caja. La interpretación de esto, es que estamos buscando un tiempo que tenga como submúltiplos al 4 y al 7.
mcm\left(4, 7\right)=4\bullet 7=49 \mathrm{m}\mathrm{i}\mathrm{n}
Deben pasar 49 minutos de la jornada laboral para que ambas cajas están ocupadas a la vez.
Comparando con las opciones, concluimos que la c) es correcta.
Reactivo 42
Luis acaba de ser contratado en una empresa que diseña líneas de transmisión de energía eléctrica. Su primer encargo es diseñar dos líneas de transmisión desde la subestación A hacia 2 empresas, una queda a 12 kilómetros y la otra a 18 kilómetros.
Para ahorrar costos, la empresa le pide a Luis que use cortes de la misma longitud para los conductores que se emplearán y que la misma sea lo más larga posible.
¿Cuál es la longitud que cumple con estas características?
- 6 kilómetros
- 2 kilómetros
- 3 kilómetros
Solución:
Haciendo a un lado el intimidante y extenuante enunciado, básicamente lo que Luis debe encontrar es la longitud máxima que permite dividir de forma exacta las distancias de 12 y 18 kilómetros. Prestemos especial atención en la palabra dividir, esto indirectamente nos dice que debemos calcular el MCD de 12 y 18.
Calculamos los divisores del 12, probamos con números hasta que el cociente sea menor o igual al divisor. Agregamos a la lista de divisores al cociente y divisor de la operación. Otra característica, es que deben encontrarse entre el 1 y el 12.
Probamos con el 2.
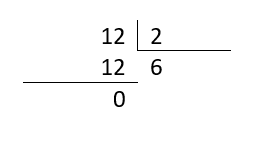
D\left(12\right)=1, 2, 6, 12
Probamos con el 3.
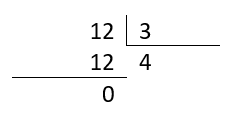
D\left(12\right)=1, 2, 3, 4, 6, 12
Probamos el 5.
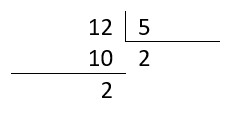
Se ha cumplido que c\le d\to 2<5 , nos detenemos en este punto. Los divisores del 12 son:
D\left(12\right)=1, 2, 3, 4, 6, 12
Si seguimos el mismo procedimiento para el 18, encontraremos que sus divisores son:
D\left(18\right)=1, 2, 3, 6, 9, 18
Ahora, solo nos queda comparar ambas listas de divisores y seleccionar el mayor que se encuentre en ambas, para este caso es el 6.
MCD\left(12, 18\right)=6
En conclusión, Luis debe seleccionar trozos de conductor eléctrico que miden 6 metros para cumplir con las políticas económicas de la empresa. Seleccionamos como respuesta correcta la opción a).
Reactivo 43
En la casa de María, el tanque de reserva tiene una capacidad total de 1500 litros. En medio de un descuido, su hermano menor dejó la llave abierta a las 7:30 am, justo antes de salir a la escuela. Cuando la familia llega a casa a las 6:30 pm, ven como cae la última gota de agua del tanque.
¿Cuál fue la razón del flujo de agua en litros por minuto?
- 1500
- 27
- 227
Solución:
Además de lamentar el grave descuido del hermano de María, debemos darnos cuenta que el enunciado nos solicita calcular la razón del agua perdida del tanque respecto del tiempo que la llave está abierta.
r=\frac{\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{s}}
Lo que debemos tener presente, es que los litros perdidos ya los tenemos de forma directa y son 1500, pero el tiempo está en horas. Transcurrieron exactamente 11 horas. Para pasarlo a minutos, multiplicamos las horas por 60 minutos.
{T}_{m}=60{T}_{h}=60 \mathrm{m}\mathrm{i}\mathrm{n}\times 11 \mathrm{h}=660\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}
Sustituimos:
r=\frac{1500 l}{660 \mathrm{m}\mathrm{i}\mathrm{n}}=2.27\frac{\mathrm{l}}{\mathrm{m}\mathrm{i}\mathrm{n}}
La razón del flujo de agua fue de 2.27 litros por cada minuto.
Concluimos indicando como respuesta correcta la opción b).
Reactivo 44
Una empresa decide adquirir una nueva máquina para mejorar su producción de botellas de su producto estrella. Si la nueva máquina es capaz de sacar 1000 envases cada 30 minutos, ¿en cuánto tiempo sacará a despacho 20000 envases?
- 200
- 600
- 800
Solución:
Para este caso, primero calculamos la razón de envases por minuto que tiene la nueva máquina:
r=\frac{1000 \mathrm{e}\mathrm{n}\mathrm{v}}{30 \mathrm{m}\mathrm{i}\mathrm{n}}=33.33\frac{\mathrm{e}\mathrm{n}\mathrm{v}}{\mathrm{m}\mathrm{i}\mathrm{n}}
Ahora, dividimos la razón por los 20000 envases para conocer en cuánto tiempo podrá sacarlos.
t=\frac{20000 \mathrm{e}\mathrm{n}\mathrm{v}}{33.33\frac{\mathrm{e}\mathrm{n}\mathrm{v}}{\mathrm{m}\mathrm{i}\mathrm{n}}}=600 \mathrm{m}\mathrm{i}\mathrm{n}
Que sería equivalente a 10 horas.
Comparando con las opciones, indicamos como correcta la opción b).
Reactivo 45
La construcción de uno de los lados de una cerca para una parcela ha tardado 18 días con unos 24 hombres trabajando en la obra. El dueño necesita disminuir el tiempo de construcción del siguiente lado a la mitad, ¿cuántos hombres debe agregar a la construcción para lograrlo?
- 30 adicionales a los 18
- 20 adicionales a los 18
- 18 adicionales a los 18
Solución:
Este problema nos plantea una relación entre el tiempo de construcción de la cerca, respecto del número de hombres que trabajan en ella. Debemos identificar el tipo de relación que poseen estas variables.
Pensemos por un momento que, naturalmente, si hay más personas trabajando en la obra el tiempo en acabar lo tiene que disminuir. Por tal motivo, la relación es inversa. Si el tiempo reducido a la mitad es de 9 días, aplicamos una regla de tres inversa:
\begin{array}{c}18\to 24\\ 9\to x\end{array}
x=\frac{18\bullet 24}{9}=48
El dueño necesita un total de 48 hombres, si ya tiene contratados a 18 entonces debe encontrar a 30 hombres más.
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 46
Una población de bacterias medida en 250 micrómetros cúbicos se alimenta de una solución que le ingresan a la placa de Petri 4 veces por día para que se mantengan nutridas, la cual dura unos 18 días antes de que el laboratorio tenga que comprar más solución. Los investigadores deciden agregar unos 50 micrómetros cúbicos de bacterias a la placa ¿Durante cuántos días se podrá alimentar a las bacterias si el alimento se reduce a 3 veces por día?
- 20 días
- 10 días
- 5 días
Solución:
En este caso el ejercicio nos plantea una regla de tres compuesta, debido a que son 3 las variables que se relacionan: el volumen de bacterias, las raciones diarias y los días que dura la solución alimenticia. Debemos organizar nuestros datos en una tabla, colocando a la incógnita en la última columna hacia la derecha.

Ahora, identificamos la relación que tiene la duración con las otras dos variables de forma independiente.
- Al aumentar el número de bacterias las raciones han disminuido: inversa
- Al bajar las raciones diarias, tiene que aumentar la duración de la solución: inversa

Para calcular a x , se iguala la razón \frac{18}{x} al producto del inverso de las razones de las otras dos variables.
\frac{18}{x}=\left(\frac{300}{250}\right)\left(\frac{3}{4}\right)\to x=\frac{18\times 250\times 4}{300\times 3}
x=20
La solución alimentaria de las bacterias durará 20 días.
Comparando con las opciones, indicamos a la a) como correcta.
Reactivo 47
Se denomina ________ al conjunto de grupos de n elementos que se forman a partir de m elementos, donde se cumple que: m>n e importa el orden.
- Combinación
- Conjunto vacío
- Variación
Solución:
El enunciado se está refiriendo a una de las técnicas de conteo. Recordemos que identificamos de cuál se trata preguntándonos inicialmente si importa o no el orden. Según la condición dada al final el orden importa, por lo que debe tratarse de una permutación.
Ahora, si el número de elementos en los grupos n es menor que el número de elementos totales: m>n , entonces estamos hablando de una variación.
Las variaciones son un tipo de permutación en la que se forman grupos de n elementos, tomados de otro grupo más grande de m elementos. En este caso importa el orden en el que se colocan los elementos para formar los grupos.
En una variación, los elementos del conjunto inicial pueden o no repetirse, en dicho caso se habla de variaciones con repetición o solo variaciones respectivamente. Considerando la descripción anterior, podemos concluir completando la frase:
Se denomina variación al conjunto de grupos de n elementos que se forman a partir de m elementos, donde se cumple que: m>n e importa el orden.
La respuesta correcta es la c).
Reactivo 48
Xavier tiene en una bolsa 3 bolas de diferente color: una roja, otra azul y una verde ¿Cuántas permutaciones se presentan si se agrupan de 2 en 2?
- 9
- 6
- 4
Solución:
El enunciado del ejercicio describe claramente el caso de una permutación en la que intervienen parcialmente los elementos, es decir, una variación. Ahora, para seleccionar qué ecuación debemos utilizar nos hacemos la pregunta: ¿hay elementos repetidos?
Las tres bolas son de colores diferentes, por lo que se trata de una variación ordinaria:
{V}_{m,n}=\frac{m!}{\left(m-n\right)!}
Para nosotros: m=3 y n=2 .
{V}_{\mathrm{3,2}}=\frac{3!}{\left(3-2\right)!}=\frac{3!}{1!}=3!=6
Existen 6 permutaciones posibles al escoger las pelotas de dos en dos.
Concluimos entonces que la respuesta correcta es la b).
Reactivo 49
El equipo de baloncesto de una secundaria necesita seleccionar al capitán, vice capitán y coordinador de los jugadores. De todos los integrantes se han presentado 9, ¿cuántas maneras existen de seleccionar los puestos vacantes?
- 230
- 504
- 606
Solución:
Antes de pensar en cualquier ecuación, debemos responder las tres preguntas clásicas en cualquier problema de conteo.
¿Importa el orden en el que quedan los jugadores?
Si importa, no será lo mismo ser el capitán que el coordinador. No puede ser combinación debe ser un tipo de permutación.
¿Intervienen todos los jugadores?
No, de los 9 jugadores solo hay 3 puestos. Tiene que tratarse de algún tipo de variación.
¿Se repiten los elementos?
No se repiten, un jugador no puede postularse a dos puestos a la vez. Se trata de una variación ordinaria.
{V}_{9, 3}=\frac{9!}{\left(9-3\right)!}=\frac{9!}{6!}=9\bullet 8\bullet 7=504
{V}_{\mathrm{9,3}}=504
Concluimos seleccionando como correcta la opción b).
Reactivo 50
Un laboratorio necesita crear un código de colores para identificar los instrumentos que poseen. Han seleccionado los colores: rojo, amarillo, verde, azul, blanco, negro y magenta.
Los códigos se forman con 5 colores y naturalmente, pueden repetirse. El jefe del laboratorio te ha asignado calcular cuántos códigos se pueden formar.
- 16800
- 16807
- 16708
Solución:
Comencemos con las preguntas básicas a la hora de resolver problemas de conteo.
¿Importa el orden en el que se colocan los colores?
Si, al cambiar de lugar alguno de los colores tenemos un código distinto. Tratamos con permutaciones.
¿Entran en juego todos los elementos?
No, los grupos se forman con 5 de los 7 colores. Es una variación.
¿Se pueden repetir elementos?
Si, el código puede ser cualquier selección de los colores dados, siempre que sean 5. Es una variación con repetición.
Variación con repetición.
V{R}_{m,n}={m}^{n}
Donde m es el total de elementos y n es la cantidad de objetos que puedo seleccionar. En nuestro caso son 7 y 5 respectivamente. Sustituimos en la ecuación.
V{R}_{m, n}={7}^{5}=16807
Se pueden crear hasta 16807 códigos distintos para el laboratorio con esta selección de colores.
Concluimos que la respuesta correcta es la opción b).

