Vas muy bien, vamos a resolver la segunda parte del examen simulacro del EXANI II de Pensamiento Matemático Versión 3. En este tutorial, resolveremos desde el reactivo 11 hasta el 20.

Resuelve los reactivos por tu cuenta antes de revisar la solución. Utiliza este material para consultas, debes desarrollar tu capacidad de analizar y resolver problemas.
Reactivo 11
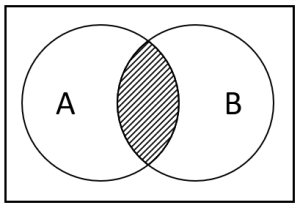
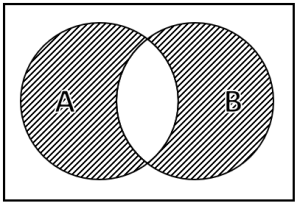
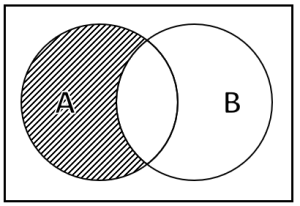
En base a la ecuación probabilística mostrada a continuación, indique cuál es el diagrama de Venn que demuestra dicha relación.
P\left(A\cap \stackrel{-}{B}\right)=P\left(A\right)-P\left(A\cap B\right)
Solución:
Para encontrar el diagrama correcto, debemos recordar algo de teoría acerca de ellos. Tengamos en cuenta que lo que encierra cada circulo, tanto A como B , son los eventos asociados a dicho fenómeno, por otro lado, la intersección entre los conjuntos corresponde a los eventos que son comunes en A y en B .
Debido a que la parte izquierda de la ecuación es menos intuitiva, trabajaremos con el miembro derecho P\left(A\right)-P\left(A\cap B\right) , el cual nos dice que tomemos los eventos del conjunto A y le restemos la intersección (el contorno central) de A con B . Dicha zona la indicamos con un sombreado.
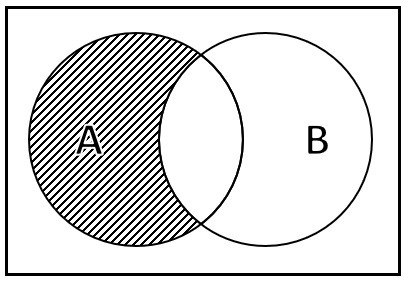
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 12
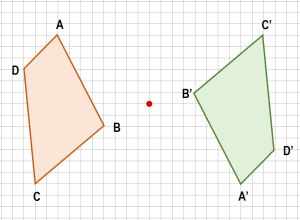
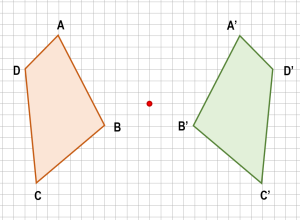
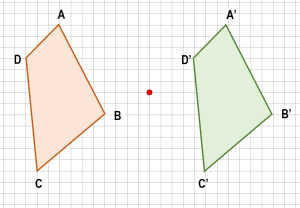
Identifique la figura que se forma al otro lado luego de aplicar una simetría central respecto al punto indicado en la imagen.
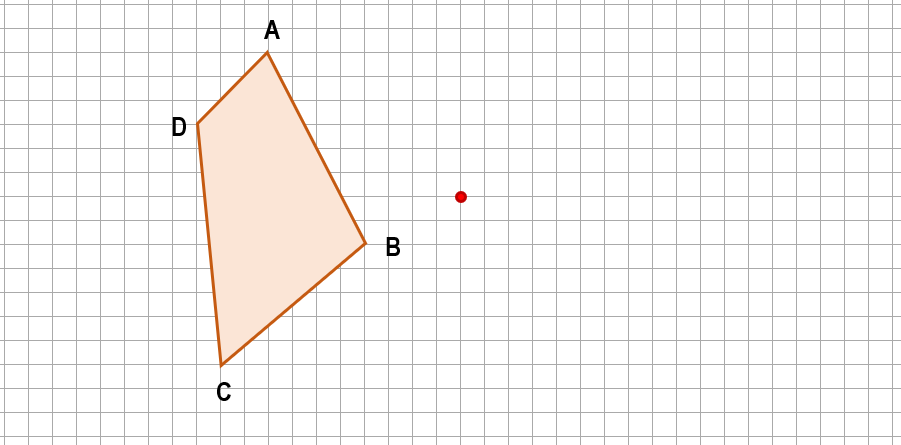
Solución:
Las simetrías respecto de un mismo punto, se hacen trazando líneas desde cualquier punto de la figura que queremos proyectar, pasando por el punto de reflexión hasta que la distancia entre el punto original y el punto de reflexión sea igual que la distancia entre el punto reflejado y el de reflexión.
Vamos a reflejar los vértices del polígono y luego unimos los puntos para formar la figura reflejada.
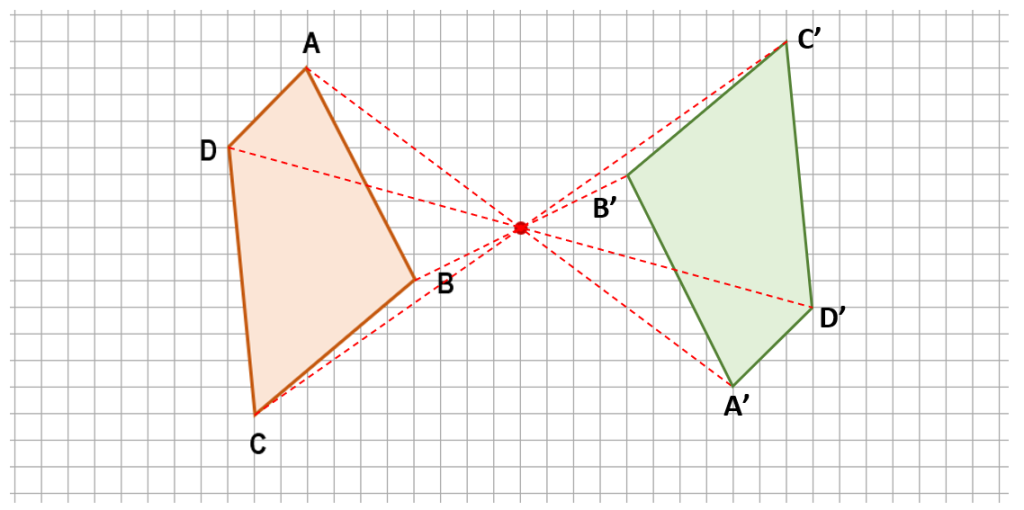
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 13
Luisa va a una tienda de repostería para comprar los ingredientes de su siguiente encargo. Ella les cobra a sus clientes el costo de los ingredientes junto al 35% por sus servicios, técnica e importes operativos.
Cuando va la caja para cancelar los ingredientes del encargo actual, la cajera le anuncia que tendrá un descuento del 25% por ser la mejor clienta de la tienda durante 2 años. Luisa es buena empresaria y sabe que debe cobrar el pastel al precio sin el descuento de la tienda.
¿Cuál es el porcentaje de ganancia de Luisa con el descuento hecho por la tienda?
- 50%
- 30%
- 46%
Solución:
Básicamente, debemos calcular cuánto va a ganar Luisa ahora que ha recibido un descuento del 25% en los ingredientes. Ya que no tenemos los precios de los productos, iniciaremos suponiendo que la cuenta total que pagó Luisa con descuento es C{T}_{d} y sin descuento es C{T}_{sd} y el cobro al cliente será CC .
La cuenta con descuento se puede escribir como:
C{T}_{d}=C{T}_{sd}\left(1-D\right)
El cobro al cliente sin tener en cuenta el descuento es:
CC=C{T}_{sd}\left(1+PG\right)
Donde PG es el porcentaje de ganancia. La ganancia bruta que recibe Luisa se calcularía, sin tener en cuenta el descuento como la resta entre el precio de venta menos el presupuesto:
G=CC-C{T}_{sd}
Ya que C{T}_{sd} se puede escribir en función del precio con el descuento, sustituimos en las ecuaciones.
C{T}_{d}=C{T}_{sd}\left(1-D\right)\to C{T}_{sd}=\frac{C{T}_{d}}{1-D}
CC=\frac{C{T}_{d}}{1-D}\left(1+PG\right)=C{T}_{d}\frac{1+PG}{1-D}
Sustituimos en la ecuación de ganancia.
G=C{T}_{d}\frac{1+PG}{1-D}-\frac{C{T}_{d}}{1-D}=C{T}_{d}\frac{PG}{1-D}
Sustituimos:
\frac{G}{C{T}_{d}}=\frac{PG}{1-D}=\frac{0.35}{1-0.25}=0.46
Gracias al descuento de la tienda, Luisa le ganará a este encargo el 46% de lo que invirtió.
Concluimos que la respuesta correcta es la opción c).
Reactivo 14
La expansión por micrómetro cuadrado de un virus es lineal y obedece la ley de 1 micrómetro cada dos días. Si el virus prolifera en condiciones de laboratorio durante medio año, ¿cuál será su expansión al cabo de este período de tiempo?
- 101 micrómetros cuadrados
- 3 micrómetros cuadrados
- 25 micrómetros cuadrados
Solución:
El enunciado nos da en este caso la siguiente proporción:
\frac{1\mu {m}^{2}}{2d}
El ritmo de crecimiento del virus es de 1 micrómetro cuadrado cada 2 días. Dejar proliferar el virus por medio año, significa mantener el experimento por \frac{365d}{2}=182.5d . Multiplicamos este número por la razón de crecimiento del virus para obtener la expansión al cabo de este tiempo.
\frac{1\mu {m}^{2}}{2d}*182.5d=91.25 \mu {m}^{2}
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 15
Determine la forma simplificada de la siguiente expresión algebraica aplicando las respectivas leyes de los exponentes.
\frac{{x}^{2}{y}^{2}-81}{{\left(xy+9\right)}^{2}\left(xy-9\right)}
- \frac{1}{81xy}
- \frac{1}{xy+9}
- xy+9
Solución:
Comenzamos por identificar que en el numerador hay una diferencia de cuadrado, la cual podemos escribir como el producto de su conjugado.
\frac{{x}^{2}{y}^{2}-81}{{\left(xy+9\right)}^{2}\left(xy-9\right)}=\frac{\left(xy+9\right)\left(xy-9\right)}{{\left(xy+9\right)}^{2}\left(xy-9\right)}
Simplificamos.
\frac{\left(xy+9\right)\left(xy-9\right)}{{\left(xy+9\right)}^{2}\left(xy-9\right)}=\frac{1}{xy+9}
Llegados a este punto, no es posible continuar simplificando.
Concluimos que la respuesta correcta es la b).
Reactivo 16
A partir de las 3 figuras mostradas en la imagen, determine el par de formas donde el área de una es tres veces el área de otra.
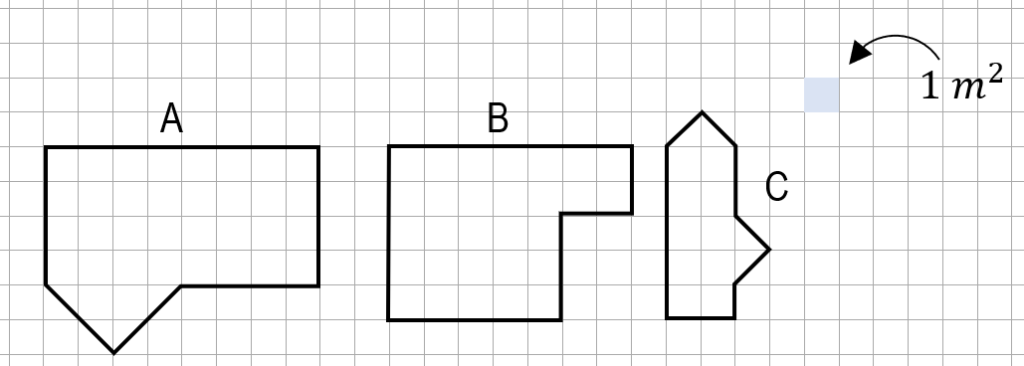
- A=3C
- C=3B
- B=3A
Solución:
Para encontrar las figuras cuyas áreas corresponden con la proporción indicada por el enunciado, debemos calcular la superficie que posee cada figura. Como las figuras están construidas sobre la cuadrícula y el área de cada cuadradito es conocida, solo debemos contar cuantos cuadritos tiene cada figura.
Comencemos por la figura A , la cual esta compuesta por un rectángulo y un triángulo, su área será la suma del área de ambas figuras. El rectángulo tiene 8\times 4 cuadritos y el triángulo 2+\frac{4}{2}=4
A=8*4+4=36 {m}^{2}
La figura B se compone de 2 cuadrados, uno 5 por 5 y otro 2 por 2.
B=5*5+2*2=29 {m}^{2}
La figura C es un rectángulo 2 por 5 y dos triángulos.
C=2*5+\frac{2}{2}+\frac{2}{2}=12 {m}^{2}
Es claro que el área de la figura B no es proporcional a ninguna otra. Si multiplicamos el área de C por 3 obtenemos 36, es decir, el área de A , por tanto:
A=3*C
La respuesta correcta es la opción a).
Reactivo 17
Sean las funciones f\left(x\right)={x}^{2}+3x+2 y g\left(x\right)=\frac{1}{x+2} , ¿cuál es el dominio de la función que resulta de sumar f+g ?
- x\in \left(-\infty ,-2\right)
- x \ne -2
- x\in \left(-2, \infty \right)
Solución:
En este caso, comenzamos por calcular la suma de ambas funciones:
f+g={x}^{2}+3x+2-\frac{1}{x+2}=\frac{{x}^{3}+5{x}^{2}+8x+5}{x+2}
Esta nueva función, a la que llamaremos q\left(x\right) está acotada siempre que el denominador sea distinto de cero.
x+2\ne 0
Despejando nos queda:
x\ne -2
Comparando con las opciones, seleccionamos como correcta la b).
Reactivo 18
Determine el espacio muestral asociado al experimento aleatorio de seleccionar los colores rojo, verde y azul de forma consecutiva y sin reemplazos.
- RRR, AAA, VVV, VRA, RVA, AVR
- RRR, AAA, VVV
- RVA, RAV, VRA, VAR, ARV, AVR
Solución:
Para encontrar el espacio muestral de este experimento aleatorio, debemos realizar su diagrama de árbol. Otra consideración que debemos tomar, es que al seleccionar un color este queda descartado para la siguiente selección.
Primera escogencia.
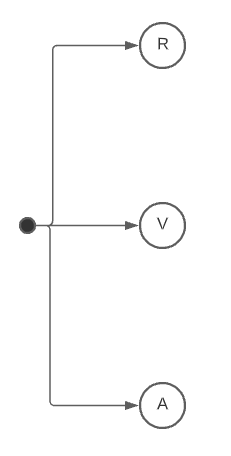
En este caso, podríamos seleccionar cualquiera de los tres colores.
Segunda escogencia.
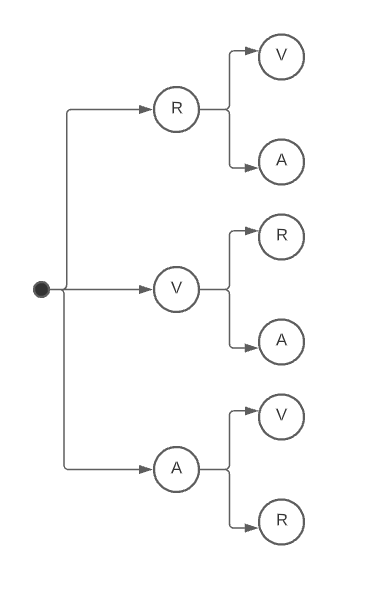
Las posibilidades se reducen a 2 y corresponden a los colores no seleccionados en la primera escogencia.
Tercera escogencia.
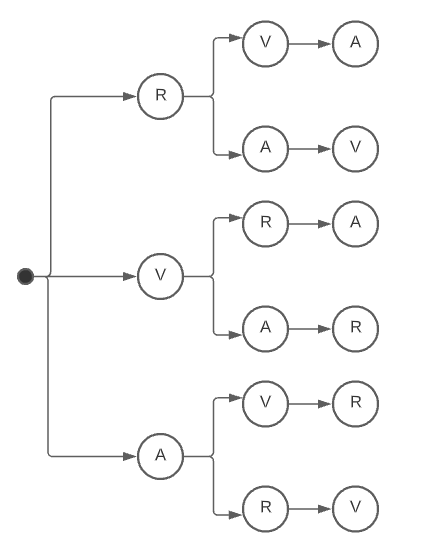
Solo queda una única posibilidad y corresponde al color que no salió en las anteriores escogencias. A partir del diagrama de árbol, obtenemos el espacio muestral:
\mathrm{R}\mathrm{V}\mathrm{A},\mathrm{ }\mathrm{R}\mathrm{A}\mathrm{V},\mathrm{ }\mathrm{V}\mathrm{R}\mathrm{A},\mathrm{ }\mathrm{V}\mathrm{A}\mathrm{R},\mathrm{ }\mathrm{A}\mathrm{V}\mathrm{R},\mathrm{ }\mathrm{A}\mathrm{R}\mathrm{V}
Comparando con las opciones, indicamos como correcta la c).
Reactivo 19
¿Es posible resolver el siguiente sistema de ecuaciones aplicando algún método conocido?
\left\{\begin{array}{c}x+y+z=1\\ x+2x+3z=4\end{array}\right.
- No es posible
- Es posible
- Depende de ciertas condiciones
Solución:
Recordemos que un sistema de ecuaciones puede ser compatible determinado o compatible indeterminado. En este último caso, el SE posee múltiples soluciones y no es posible obtener una única solución.
Cuando el enunciado se refiere a “resolver el sistema de ecuaciones”, hace alusión a encontrar el valor de todas las incógnitas, lo cual es imposible en este caso porque hay más incógnitas que ecuaciones. Existen infinitas soluciones para el sistema.
Concluimos entonces que la respuesta correcta es la opción a).
Reactivo 20
Una empresa ha evaluado la probabilidad de que el nuevo producto que están elaborando tenga un desperfecto de fábrica. Se manufacturaron 100 piezas, de las cuales 5 han resultado ser defectuosas.
¿Cuál es la probabilidad de sacar de este lote dos piezas en mal estado de forma consecutiva?
- 0.004
- 0.005
- 0.002
Solución:
En este problema debemos calcular la probabilidad consecutiva de sacar dos piezas defectuosas, una luego de la otra. Para la primera extracción, tenemos 100 piezas y de ellas 5 son defectuosas; la probabilidad de extraer una es:
\frac{5}{100}
Ahora, se intenta sacar otra pieza, de las cuales quedan 99 y solo 4 de ellas son defectuosas. La probabilidad de extraer otra defectuosa es:
\frac{5}{100}*\frac{4}{99}=0.002
En porcentaje, esto sería: 0.2% de posibilidades de sacar dos veces una pieza defectuosa.
Comparando con las opciones, la respuesta correcta es la c).