Llegamos a la tercera y última parte del simulacro resuelto de Pensamiento Matemático para el examen de ingreso diseñado por Ceneval. Esta vez vamos por los reactivos del 21 al 30.
Estos ejercicios, al igual que los anteriores, tienen la misma estructura y abarcan los temas de la prueba real Exani. Resuélvelos por tu cuenta antes de mirar la solución, obtener una buena calificación depende de las ganas que pongas durante tu preparación.
Ejercicios de Pensamiento Matemático
Vamos con los últimos 10 reactivos de Pensamiento Matemático. Al finalizar este simulacro, habrás repasado todos los temas de matemáticas que van para el examen, poniendo en práctica estos conocimientos con ejercicios similares a los de la prueba real.
Reactivo 21
Dado el siguiente sistema de ecuaciones:
\left\{\begin{array}{c}2x+3y=4\\ 5x+6y=7\\ 7x+9y=11\end{array}\right.
¿Cuál de las tres ecuaciones se puede eliminar y el SE resultante es equivalente?
- 2x+3y=4
- 5x+6y=7
- 7x+9y=11
Solución:
Decimos que dos sistemas de ecuaciones son equivalentes cuando tienen las mismas soluciones. Además, deben tener el mismo número de variables, pero no necesariamente el mismo número de ecuaciones.
Esto nos da una pista del resultado: un sistema de 2 variables, pero con una ecuación menos. Nuestro trabajo es encontrar qué ecuación debemos eliminar y por qué. Existen dos criterios de equivalencia: producto por un número distinto de cero y suma de ecuaciones.
En este caso, los coeficientes de las variables no son múltiplos entre ellas, la única posibilidad de equivalencia es a través de la suma de ecuaciones. Si examinamos al sistema de ecuaciones, sumando 2x+3y=4 con 5x+6y=7 se obtiene la tercera ecuación 7x+9y=11 .
Concluimos que eliminar a 7x+9y=11 hace permanecer equivalente al SEL.
Concluimos que la respuesta correcta es la c).
Reactivo 22
Calcula el valor de la \mathrm{sec}\alpha si \mathrm{tan}\alpha =\frac{1}{\sqrt{3}} .
- \frac{2}{\sqrt{3}}
- \frac{1}{2}
- \frac{3}{2}
Solución:
Para encontrar el valor de la secante del ángulo, debemos emplear una identidad trigonométrica que relacione a la tangente con la secante. Examinando entre las fórmulas básicas, tenemos que la identidad pitagórica en términos de la secante y tangente es lo que necesitamos.
{\mathrm{tan}}^{2}\alpha +1={\mathrm{sec}}^{2}\alpha
Despejamos aplicando raíz cuadrada en ambos miembros de la identidad.
\sqrt{{\mathrm{tan}}^{2}\alpha +1}=\sqrt{{\mathrm{sec}}^{2}\alpha }
\therefore \mathrm{sec}\alpha =\pm \sqrt{{\mathrm{tan}}^{2}\alpha +1}
Ahora, ¿qué valor debemos tomar? Como sabrás, al despejar una raíz cuadrada se obtienen dos posibles resultados: uno positivo y otro negativo. Para esto, debemos identificar el cuadrante en el que se encuentra \mathrm{tan}\alpha =\frac{1}{\sqrt{3}} .
La tangente es positiva en el primer y tercer cuadrante, mientras que la secante es positiva en el primer y cuarto cuadrante. La tangente vale \frac{1}{\sqrt{3}} en 30° y en 210°.
Para efectos de este ejercicio, supondremos que trabajamos en el primer cuadrante, lugar donde la secante es también positiva y, por tanto, el resultado válido es el de la raíz positiva.
\mathrm{sec}\alpha =\sqrt{{\mathrm{tan}}^{2}\alpha +1}
Sustituimos.
\mathrm{sec}\alpha =\sqrt{{\left(\frac{1}{\sqrt{3}}\right)}^{2}+1}=\sqrt{\frac{1}{3}+1}=\sqrt{\frac{4}{3}}
\mathrm{sec}\alpha =\frac{2}{\sqrt{3}}
Comparando con las opciones, seleccionamos como correcta la opción a).
Reactivo 23
A partir de la circunferencia que tiene como lugar geométrico {\left(x+2\right)}^{2}+{y}^{2}=4 y cuya gráfica es:
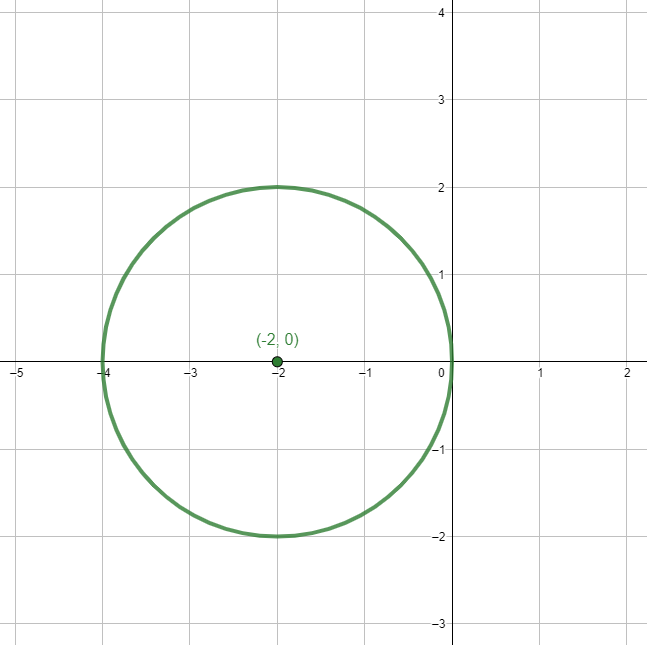
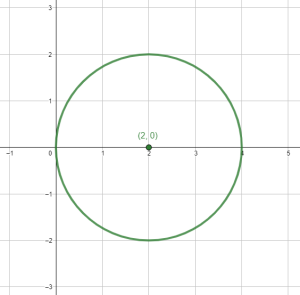
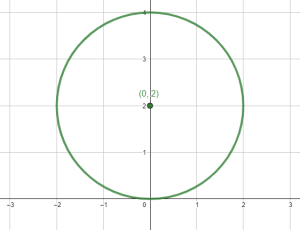
¿Cuál es la gráfica si la circunferencia se traslada 2 unidades a la derecha?
Solución:
Para trasladar cualquier lugar geométrico sobre el eje de las x , debemos tener en cuenta hacia qué lado se va a trasladar. El enunciado dice que es hacia la derecha, es decir, en dirección de las x positivas.
Esto lo logramos restando la cantidad que nos queremos mover hacia la derecha en los lugares donde se encuentra la x . A fines de este problema, debemos movernos 2 unidades a la derecha, es decir, debemos restar 2 en los lugares donde se encuentra la x .
{\left(x+2-2\right)}^{2}+{y}^{2}=4\to {\left(x\right)}^{2}+{y}^{2}=4
\therefore {x}^{2}+{y}^{2}=4
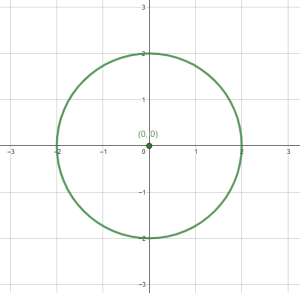
Nos queda una circunferencia centrada en el origen.
Comparando con las opciones, la respuesta correcta es la c), una circunferencia con centro en el origen y radio igual a 2.
Reactivo 24
Un árbol proyecta una sombra a las 3:00 pm de 3 metros de longitud. ¿Cómo podría medirse la altura del árbol de forma indirecta?
- Midiendo la altura del árbol metro a metro hasta la copa
- Midiendo la sombra y la altura de un objeto más pequeño a la misma hora
- Midiendo la sombra del árbol al medio día
Solución:
Gracias a que el sol es un cuerpo masivo que se encuentra a una distancia en demasía lejana si la comparamos con la altura de un árbol, el ángulo de incidencia de los rayos de sol se considera igual para cualquier objeto que se encuentre cerca del árbol a esa misma hora del día (3:00 pm).
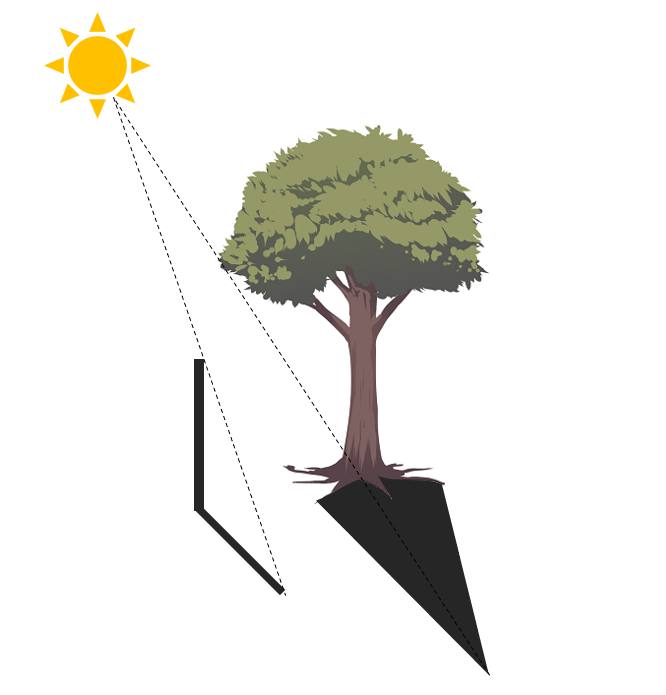
De esta forma, las sombras se forman por rayos que tienen el mismo ángulo de incidencia, permitiendo aplicar triángulos semejantes entre la altura del árbol y del objeto, junto a la medida de las sombras de cada objeto.
En conclusión: calcular la altura del árbol es muy fácil si medimos la altura y sombra de otro objeto más pequeño. La respuesta correcta es la opción b).
Reactivo 25
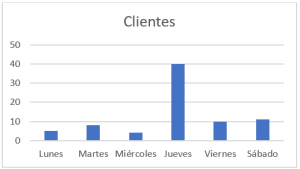
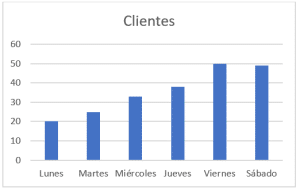
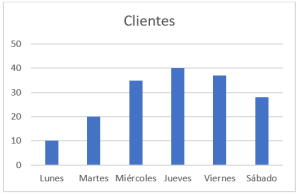
El siguiente gráfico de pastel muestra el número de clientes que ha tenido una tienda cada día de la semana.
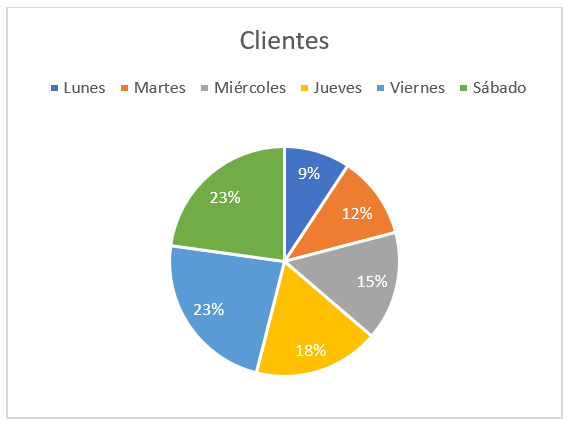
Seleccione el histograma de frecuencia que corresponde con el gráfico de pastel.
Solución:
Para resolver este ejercicio, debemos comparar las proporciones del gráfico circular con las proporciones de las barras en los gráficos de barras en los incisos.
Es necesario hacer énfasis en esto último, ya que la escala del gráfico de pastel no pareciera coincidir con ningún inciso, sólo nos interesa que se respeten las proporciones.
El primer gráfico de barra queda descartado por completo, ya que las porciones aumentan de tamaño sucesivamente hasta el viernes y sábado que son iguales. Algo similar sucede con el tercer gráfico, las barras tienen forma de distribución normal y no de crecimiento progresivo.
El segundo concuerda a la perfección, cada barra es mayor a la anterior y las últimas dos miden técnicamente igual. Concluimos entonces que la respuesta correcta es la b).
Reactivo 26
La producción en una planta de dispositivos electrónicos se registra, mes a mes, en la siguiente tabla.
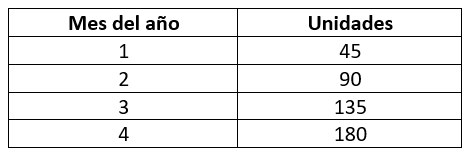
Determina el modelo matemático que corresponde con los datos y la producción para el mes 5.
- y=2x-2, y\left(5\right)=8
- y=-\frac{x}{5}+6, y\left(5\right)=5
- y=45x, y\left(5\right)=225
Solución:
El primer modelo que debemos considerar en estos casos es el lineal, por ser más simple de comprobar. Iniciamos calculando que la pendiente entre los datos consecutivos sea igual, de ser así, el modelo es una línea recta.
{m}_{1}=\frac{90-45}{2-1}=45
{m}_{2}=\frac{135-90}{3-2}=45
{m}_{3}=\frac{180-135}{4-3}=45
Los datos corresponden a una línea recta.
Calculada la pendiente ( m=45 ), nos queda sustituir un punto que pertenezca a ella para obtener la fórmula matemática.
y-{y}_{0}=m\left(x-{x}_{0}\right)
Escogemos como punto \left({x}_{0},{y}_{0}\right)=\left(1, 45\right) .
y-45=45\left(x-1\right)\to y=45x
Finalmente, sustituimos x=5 para obtener la producción en el quinto mes.
y\left(5\right)=45\left(5\right)=225
y=45x;y\left(5\right)=225
Comparando con las opciones, escogemos como correcta la c).
Reactivo 27
El siguiente histograma de frecuencias muestra la distribución de personas que cruzan la frontera entre dos países día tras día, durante una semana.
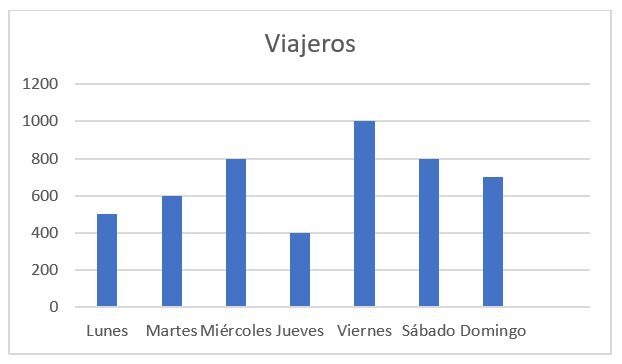
¿Cuál de las siguientes aseveraciones es correcta?
- Los últimos tres días de la semana tienen mayor flujo de viajeros que la media de la muestra
- Los días que más se alejan de la media son: el domingo y el jueves
- La muestra se concentra en los primeros 3 días de la semana
Solución:
Debemos comprobar cuál de las tres aseveraciones es instancia de algo cierto en el gráfico del enunciado. La primera es totalmente cierta, si calculamos la media del flujo de pasajeros obtenemos que es aproximadamente 686, y el flujo en los últimos tres días suma un total de 2500.
La segunda es falsa, ya que solo el jueves se aleja de la media, pero el domingo tuvo un flujo de pasajeros igual a 700.
La última es de nuevo falsa, el mayor flujo de pasajeros está concentrado en los 3 últimos días de la semana.
Concluimos entonces que la respuesta correcta es la a).
Reactivo 28
Una función cuadrática de la forma y=a{x}^{2}+bx+c , tiene su vértice en el punto:
V\left(\frac{-b}{2a},-\frac{{b}^{2}-4ac}{4a}\right)
Si la ordenada del vértice es igual a cero, ¿Qué condición deben cumplir a y b para que la abscisa del vértice sea siempre positiva?
- b<0, a y c>0
- b>0, a y c>0
- No tiene solución
Solución:
La abscisa del vértice de la parábola tiene como valor \frac{-b}{2a} , para que la misma sea siempre positiva debemos resolver la siguiente inecuación:
-\frac{b}{2a}>0
Pero dicha desigualdad es positiva en dos casos: para b<0 y a>0 o para a<0 y b>0 . Otro dato que nos ofrece el enunciado, es que la ordenada es igual a cero.
-\frac{{b}^{2}-4ac}{4a}=0
Despejando obtenemos:
{b}^{2}=4ac
Esto fuerza a que el producto ac deba ser positivo, condición que se cumple para:
a>0 y c>0
a<0 y c<0
Tenemos entonces las siguientes posibilidades para que el vértice se mantenga del lado positivo de las x :
Si b<0 , a y c>0 y {b}^{2}=4ac .
Si b>0 , a y c<0 y {b}^{2}=4ac .
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 29
Un grupo de investigación necesita seleccionar un instrumento de medición para realizar un estudio a nivel celular. El equipo de instrumentación redujo la búsqueda a dos empresas que ofrecen equipos con una baja desviación respecto a la media. La siguiente tabla contiene 5 mediciones realizadas con ambos instrumentos.
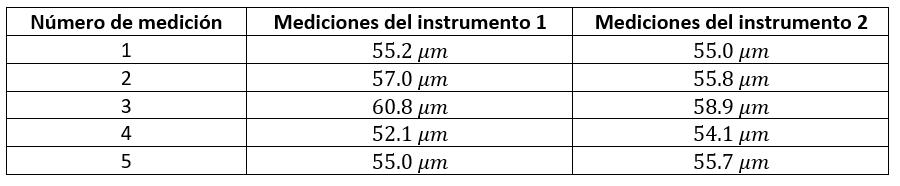
¿Cuál de ellos es el indicado, si desean obtener mediciones lo más cercanas posibles?
- 1
- 2
- Ambos
Solución:
Para escoger uno u otro instrumento, es necesario determinar el nivel de desviación entre las mediciones de los instrumentos, es decir, debemos utilizar un parámetro estadístico que nos permita obtener la desviación respecto de la media, tal como la varianza o la desviación estándar.
Cálculos para el instrumento 1
{\stackrel{-}{x}}_{1}=\frac{55.2+57+60.8+52.1+55}{5}=56
Fórmula de la varianza:
{s}^{2}=\sum \frac{{\left({x}_{i}-{\stackrel{-}{x}}_{1}\right)}^{2}}{n-1}
{s}_{1}^{2}=10.2
Cálculos para el instrumento 2
{\stackrel{-}{x}}_{2}=\frac{55+55.8+58.9+54.1+55.7}{5}=55.9
Fórmula de la varianza:
{s}^{2}=\sum \frac{{\left({x}_{i}-{\stackrel{-}{x}}_{1}\right)}^{2}}{n-1}
{s}_{2}^{2}=3.2
Debido a que la varianza del instrumento 2 es menor, será este el dispositivo seleccionado. Comparando con las opciones, la respuesta correcta es la b).
Reactivo 30
En el siguiente histograma de frecuencia, se registraron los datos recolectados a partir de un estudio estadístico a una población, relacionados con el tipo de transporte que usan los habitantes.
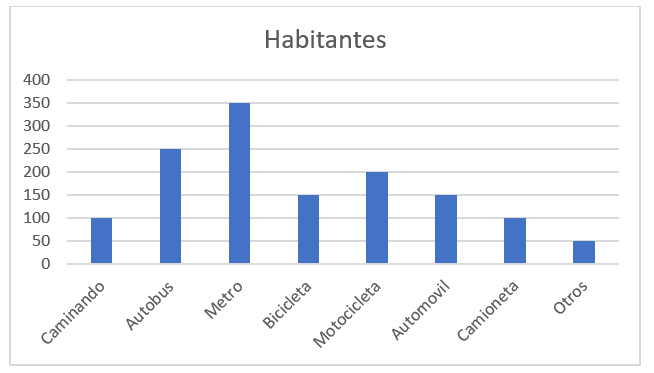
La finalidad del estudio, es determinar el porcentaje de individuos que no poseen vehículo de transporte propio.
- 51.85%
- 60%
- 33.33%
Solución:
Debemos calcular la cantidad de personas que no tienen vehículo propio y luego dividirlo entre el total de personas en el estudio. El histograma muestra 3 grupos que se desplazan: caminando, autobús y metro. Sumando la población de los 3 grupos obtenemos:
Población sin vehículo=100+250+350=700
La población total es:
Población total=700+150+200+150+100+50=1350
El porcentaje se calcula como:
{\%}_{sv}=\frac{700}{1350}*100\%=51.85\%
Comparando con las opciones, la respuesta correcta es la a).