Hola de nuevo, aspirante. En esta parte del simulador vamos con uno de los temas que más aparece en geometría plana (o geometría euclidiana): áreas entre dos figuras. Este es el típico bloque donde el examen te mezcla figuras y te pide el área sombreada, el área “faltante” o el área que queda después de recortar algo.
Aquí no basta con memorizar fórmulas. Lo que de verdad te hace sacar el punto es identificar rápido qué área es la figura completa y qué área se le quita. En la mayoría de los reactivos la operación clave es: resta de áreas (aunque en pocos casos toca sumar).
En los Reactivos 1 al 10 vas a practicar justo lo que más preguntan en exámenes como UNAM, IPN y EXANI II:
- Figuras inscritas (circunferencias dentro de cuadrados o rectángulos).
- Cuartos y semicircunferencias dentro de polígonos (sumas y restas de “pedazos” de círculo).
- Anillo circular (dos círculos concéntricos: área grande menos área chica).
- Figuras compuestas tipo “ventana bizantina” (rectángulos + semicírculos).
- Zonas sombreadas con cuadrados y diagonales (usar pitágoras/propiedades del cuadrado cuando te dan la diagonal).
Tip rápido antes de empezar: cada vez que veas “área sombreada”, piensa primero en esto:
¿Qué figura me conviene calcular completa? y luego ¿qué parte le tengo que quitar?. Si lo haces así, te evitas el error clásico de querer calcular “la sombrita” directo sin un plan.
Y ojo: en varios reactivos te dan π = 3.14. Úsalo tal cual para que tus resultados coincidan con las opciones.
Listo. Respira, concéntrate y vámonos con el primer reactivo.
Reactivo 1
Se inscribe una circunferencia de radio 6 cm en un cuadrado, determina el área sombreada.
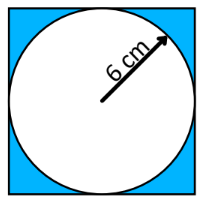
Considera \pi = 3.14
Reactivo 2
En cada una de las esquinas de un cuadrado de lado 16 cm, se tienen cuartos de circunferencia de radio 4 cm con centro en cada uno de los vértices del cuadrado, determina el área sombreada.
Considera \pi = 3.14
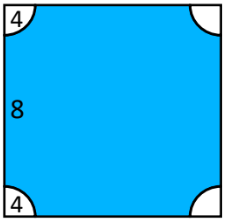
Reactivo 3
Se inscriben 2 circunferencias de radio 3 cm en un rectángulo, determina el área sombreada.
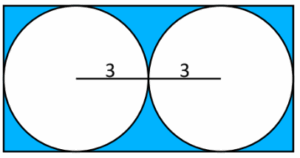
Considera \pi = 3.14
Reactivo 4
Se tienen 2 círculos concéntricos, determina el área del anillo circular si el radio de uno de ellos es el doble del otro.
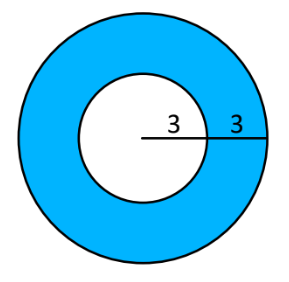
Considera \pi = 3.14
Reactivo 5
En un cuadrado ABCD de lado 10 cm se inscriben 2 semicircunferencias, como se muestra en la figura. Encuentra el área sombreada.
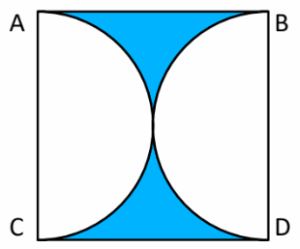
Considera \pi = 3.14
Reactivo 6
La figura ABCD es un cuadrado y r = 4 cm. Determina el área sombreada si R = 6 cm.
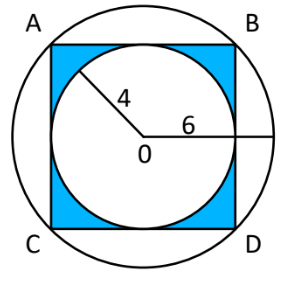
Considera \pi = 3.14
Reactivo 7
Calcula la cantidad de vitral opaco que se necesita en la siguiente ventana de tipo bizantino.
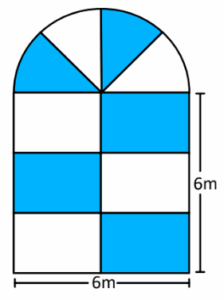
Considera \pi = 3.14
Reactivo 8
Determina el área de la zona sombreada en la siguiente figura si el diámetro del círculo mayor mide 18 cm.
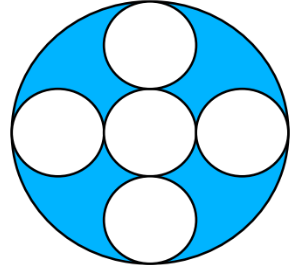
Considera \pi = 3.14
Reactivo 9
Determina el área de la zona sombreada si ABCD y DCFE son cuadrados de lado 1 cm.
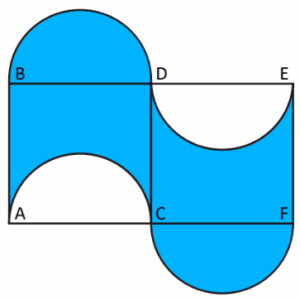
Reactivo 10
Encuentra el área de la zona sombreada si \overline{AC} = \sqrt{2} cm y ABCD es un cuadrado.
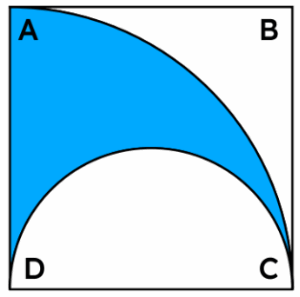
Considera \pi = 3.14


