¡Hola aspirante! Iniciamos la solución del examen simulacro para la Guía EXANI II, en el módulo de Cálculo Diferencial e Integral. En este tutorial resolveremos la primera parte, desde el reactivo 1 hasta el 30.
Antes de resolver los ejercicios de cálculo, es importante que refuerces tus conocimientos en álgebra y trigonometría. Esto te permitirá resolver los ejercicios con mayor rapidez.
Estructura del EXANI II
El examen de ingreso EXANI II está compuesto por dos partes: una de habilidades y conocimientos y otra con los módulos específicos.
Además, algunas universidades aplican una prueba diagnóstica de inglés adicional, la cual no cuenta en para la calificación final.
Examen de habilidades y conocimientos
La primera parte del EXANI II se aplica para todas las carreras y se compone de 90 reactivos: 60 de Español y 30 de Matemáticas. En la siguiente tabla se encuentra la distribución de los reactivos del EXANI II:
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Conocimientos específicos del EXANI II posee un total de 15 módulos, entre los que se encuentra Cálculo Diferencial e Integral.
Todos los estudiantes deben responder 2 módulos en esta segunda parte, los cuales varían de acuerdo con la carrera. Es necesario que revises la convocatoria de tu universidad para conocer qué módulos van para tu examen.
Módulos de los conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Cálculo EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de cálculo diferencial e integral, con el temario desglosado que va para el examen.
| Subáreas | Temas | Num. de reactivos |
|---|---|---|
| Cálculo diferencial | Límites | 12 |
| La derivada | ||
| Aplicaciones de la derivada | ||
| Cálculo Integral | La integral | 12 |
| Métodos de integración | ||
| Aplicaciones de la integral definida | ||
| Total | 24 |
Recomendaciones para resolver la guía
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Curso Exani II 2024
Reactivo 1
Dada la siguiente función, determina el conjunto de valores que corresponden a su dominio.
f\left(x\right)=\sqrt{49-{x}^{2}}
- x\in \left[-7, 7\right]
- x\in \left[-7, 7\right)
- x\in \left[0, 7\right)
Solución:
Para calcular el dominio de cualquier función real, debemos identificar cuáles son las funciones elementales que componen a f\left(x\right) , además de conocer cuáles son sus restricciones. En este caso, f\left(x\right) es una función radical, cuya restricción es que el radicando sea mayor o igual que cero.
49-{x}^{2}\ge 0
Para resolver esta desigualdad, es necesario realizar un estudio de signos sobre el binomio de la izquierda factorizado. Factorizamos aplicando diferencia de cuadrados.
\left(7-x\right)\left(7+x\right)\ge 0
Las raíces del binomio son: 7 y -7 . El estudio de signos quedaría:
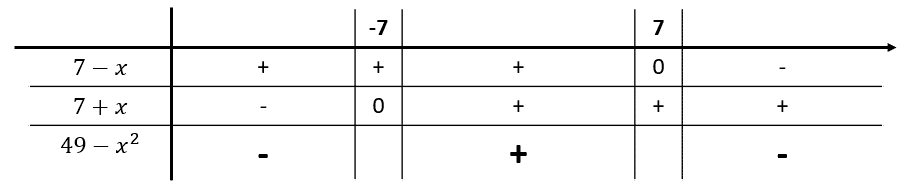
El único intervalo de valores en el que el binomio es positivo o igual a cero es entre -7 y 7. Expresando la solución en notación de conjunto nos queda:
x\in \left[-7, 7\right]
La respuesta correcta es el inciso a).
Reactivo 2
Determina el rango de la siguiente función:
g\left(x\right)={x}^{2}-1
- R:\left(-1, \infty \right)
- R:\left(1, \infty \right)
- R:\left[-1, \infty \right)
Solución:
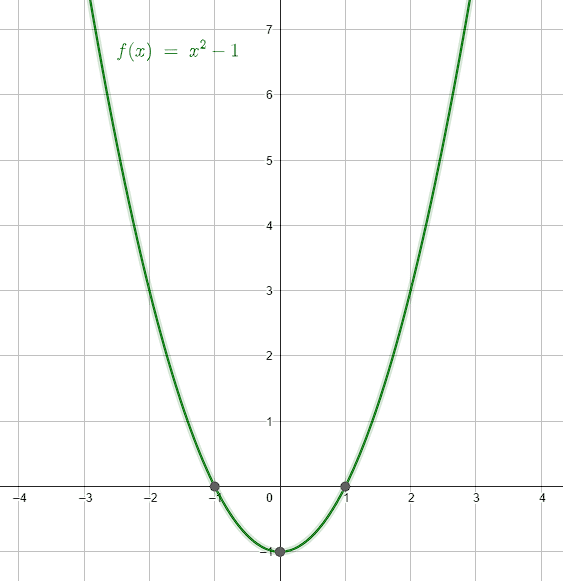
Para encontrar el rango de una función real, tenemos tres métodos: conocer la función, de forma gráfica o calculando el dominio de la inversa. Si examinamos la función, esta corresponde con una parábola.
El rango de una parábola vertical está definido de dos formas, según si abre hacia arriba o hacia abajo.
- Parábola que abre hacia arriba: y\in \left[{v}_{y}, \infty \right)
- Parábola que abre hacia abajo: y\in \left(-\infty , {v}_{y}\right]
Donde {v}_{y} es la coordenada vertical del vértice de la parábola. La parábola del enunciado abre hacia arriba y su vértice lo podemos obtener fácilmente reordenando a la expresión:
y={x}^{2}-1\to y+1={x}^{2}
Comparando con la forma ordinaria de la parábola:
4p\left(y-k\right)={\left(x-h\right)}^{2}
El vértice es:
\left(h, k\right)=\left(0, -1\right)
Finalmente, el rango de la función g\left(x\right)={x}^{2}-1 es:
y\in \left[-1, \infty \right)
Concluimos que la respuesta correcta es el inciso c).
Reactivo 3
Dadas las funciones f\left(x\right) y g\left(x\right) , determine la composición \left(f○g\right)\left(x\right) .
f\left(x\right)=\frac{x}{x-1}
g\left(x\right)=\frac{x}{x+1}
- \left(f○g\right)\left(x\right)=-x
- \left(f○g\right)\left(x\right)=\frac{1}{x}
- \left(f○g\right)\left(x\right)=-\frac{x}{{x}^{2}-1}
Solución:
En todo problema de composición de funciones, lo único que debemos tener en cuenta es que f○g significa: a la función f\left(x\right) le sustituimos todas las x por la función g\left(x\right) .
Llevando a cabo lo anterior nos queda:
\left(f○g\right)\left(x\right)=\frac{\frac{x}{x+1}}{\frac{x}{x+1}-1}
Simplificamos.
\left(f○g\right)\left(x\right)=\frac{\frac{x}{x+1}}{\frac{x-x-1}{x+1}}=\frac{\frac{x}{x+1}}{\frac{-1}{x+1}}=-x
Finalmente:
\left(f○g\right)\left(x\right)=-x
Indicamos como respuesta correcta al inciso a).
Reactivo 4
Al estudiar el límite de cierta función real, se obtiene el siguiente resultado:
\underset{x\to \infty }{\mathrm{lim}}f\left(x\right)=L
¿Cuál sería la interpretación geométrica de dicho resultado?
- Cuando la variable x tiende a un valor finito, la función f se vuelve finita
- Cuando la variable x tiende a un valor muy grande, la función f se establece en un valor finito
- Que la función f no está definida cuando x=L
Solución:
Los límites al infinito estudian lo que sucede con las funciones cuando la variable independiente (en la mayoría de casos x ) crece hacia un valor muy grande. Si la función parece acercarse asintóticamente a un valor finito, en este caso L , decimos que la función tiende a L .
Teniendo en cuenta esto y examinando los incisos, concluimos que la respuesta correcta es b).
Reactivo 5
Dada la siguiente gráfica de la función f\left(x\right) , indique el valor de los límites solicitados.
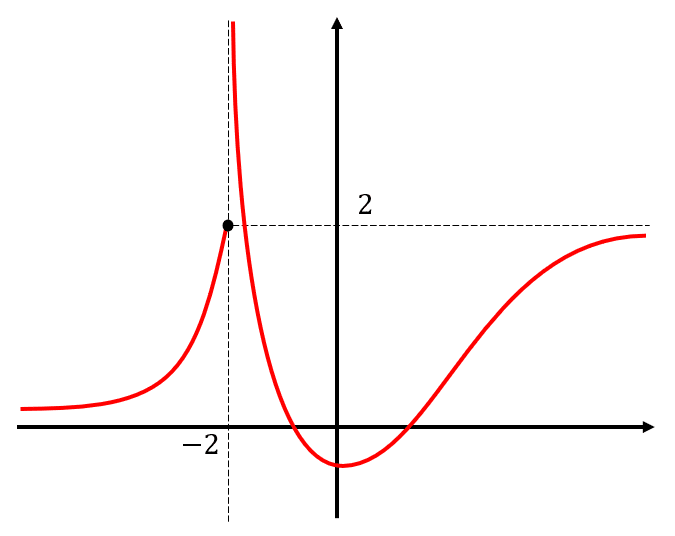
- \underset{x\to -{2}^{+}}{\mathrm{lim}}f\left(x\right)
- \underset{x\to -{2}^{-}}{\mathrm{lim}}f\left(x\right)
- \underset{x\to -\infty }{\mathrm{lim}}f\left(x\right)
- \underset{x\to \infty }{\mathrm{lim}}f\left(x\right)
- \infty , 2, 0, 2
- -\infty , -2, 0,-2
- 0, -2, \infty , 2
Solución:
Para encontrar el valor de cada límite, debemos ir examinando lo que sucede en la gráfica de la función cuando nos acercamos a determinado valor.
Primer límite.
\underset{x\to -{2}^{+}}{\mathrm{lim}}f\left(x\right)
Es el límite lateral cuando x tiende a -2 por la derecha.
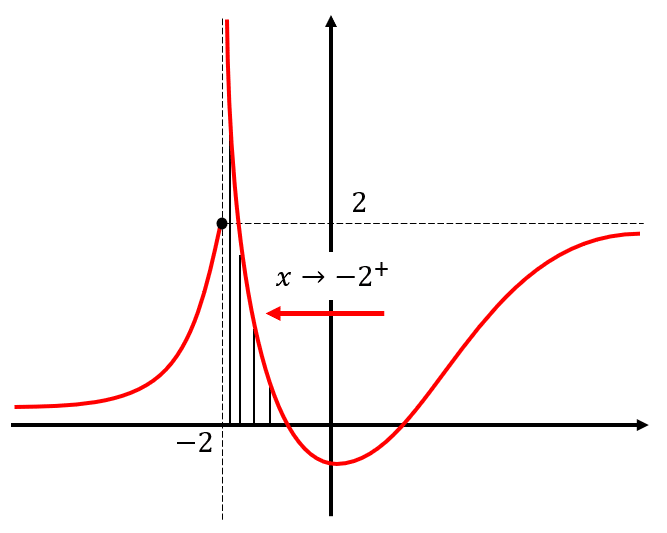
A medida que nos acercamos a la función por la izquierda, su valor crece hacia +\infty .
\underset{x\to -{2}^{+}}{\mathrm{lim}}f\left(x\right)=\infty
Segundo límite.
\underset{x\to -{2}^{-}}{\mathrm{lim}}f\left(x\right)
Es el límite lateral cuando x tiende a -2 por la izquierda. En este caso, la función se encuentra definida y vale f\left({2}^{-}\right)=2 .
Tercer límite.
\underset{x\to -\infty }{\mathrm{lim}}f\left(x\right)
Examinando la gráfica de la función, a medida que la variable x se hace cada vez más negativa, la función se acerca a cero.
\underset{x\to -\infty }{\mathrm{lim}}f\left(x\right)=0
Cuarto límite.
\underset{x\to \infty }{\mathrm{lim}}f\left(x\right)
Empleando el mismo razonamiento, vemos que la función se acerca a 2 cuando x crece infinitamente.
\underset{x\to \infty }{\mathrm{lim}}f\left(x\right)=2
Uniendo todas las respuestas parciales: \infty , 2, 0, 2 .
Concluimos el problema indicando como respuesta correcta al inciso a).
Reactivo 6
Calcule el valor del siguiente límite.
\underset{a\to 5}{\mathrm{lim}}\frac{a-5}{{a}^{2}-25}
- L={10}^{-1}
- L=10
- L=5
Solución:
Iniciamos evaluando el límite en el punto.
\underset{a\to 5}{\mathrm{lim}}\frac{a-5}{{a}^{2}-25}=\frac{5-5}{{5}^{2}-25}=\frac{0}{0}
Tenemos una indeterminación. Factorizamos el denominador aplicando diferencia de cuadrados.
\underset{a\to 5}{\mathrm{lim}}\frac{a-5}{{a}^{2}-25}=\underset{a\to 5}{\mathrm{lim}}\frac{a-5}{\left(a-5\right)\left(a+5\right)}=\underset{a\to 5}{\mathrm{lim}}\frac{1}{a+5}
Evaluamos para comprobar.
\underset{a\to 5}{\mathrm{lim}}\frac{1}{a+5}=\frac{1}{5+5}=\frac{1}{10}
Este resultado puede expresarse como \frac{1}{10}={10}^{-1} . Finalmente:
\underset{a\to 5}{\mathrm{lim}}\frac{a-5}{{a}^{2}-25}={10}^{-1}
Indicamos como respuesta correcta al inciso a).
Reactivo 7
Determine el valor del límite de la función f\left(x\right)=\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4} cuando x tiende a 2.
- L=\frac{1}{6}
- L=-\frac{1}{6}
- L=-1
Solución:
Comenzamos expresando al límite en lenguaje matemático.
\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}
Evaluamos el límite para comprobar la indeterminación.
\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}=\frac{2-\sqrt[3]{2\cdot {2}^{2}}}{{2}^{2}-4}=\frac{2-\sqrt[3]{8}}{4-4}=\frac{2-2}{0}=\frac{0}{0}
Se presenta una indeterminación 0/0 .
Debido a que la raíz del numerador es cúbica, no lograremos nada factorizando el denominador por diferencia de cuadrados. Debemos encontrar una forma de factorizar el numerador. Debido a que en el numerador hay una raíz cúbica, vamos a aplicar la factorización de la diferencia de cubos.
{a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)
El truco en estos casos, es hacer que 2-\sqrt[3]{2{x}^{2}}=a-b , por tanto:
a=2, b=\sqrt[3]{2{x}^{2}}
Despejamos a a-b de la expresión de la factorización:
{a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)\to a-b=\frac{{a}^{3}-{b}^{3}}{{a}^{2}+ab+{b}^{2}}
Aplicando esto a nuestra expresión:
2-\sqrt[3]{2{x}^{2}}=\frac{8-2{x}^{2}}{4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}}=\frac{8-2{x}^{2}}{4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}}
Sustituimos en el límite.
\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}=\underset{x\to 2}{\mathrm{lim}}\frac{\frac{8-2{x}^{2}}{4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}}}{{x}^{2}-4}
\underset{x\to 2}{\mathrm{lim}}\frac{8-2{x}^{2}}{\left(4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}\right)\left({x}^{2}-4\right)}
Extraemos factor común del numerador -2.
-2\underset{x\to 2}{\mathrm{lim}}\frac{{x}^{2}-4}{\left(4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}\right)\left({x}^{2}-4\right)}=-2\underset{x\to 2}{\mathrm{lim}}\frac{1}{4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}}
Evaluamos.
-2\underset{x\to 2}{\mathrm{lim}}\frac{1}{4+2\sqrt[3]{2{x}^{2}}+{\left(\sqrt[3]{2{x}^{2}}\right)}^{2}}=\frac{-2}{4+2\sqrt[3]{2{\left(2\right)}^{2}}+{\left(\sqrt[3]{2{\left(2\right)}^{2}}\right)}^{2}}=-\frac{2}{4+4+4}
-\frac{2}{4+4+4}=-\frac{1}{6}
Finalmente:
\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}=-\frac{1}{6}
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 8
Calcule el límite de la función cuando la variable tiende a infinito.
\underset{x\to \infty }{\mathrm{lim}}\frac{\sqrt{{x}^{2}+3x}}{x}
- L=0
- L=1
- L=-1
Solución:
Sin evaluar el límite, sabemos que la indeterminación es \infty /\infty . Iniciamos la solución elevando al cuadrado y aplicando raíz cuadrada a la x del denominador.
\underset{x\to \infty }{\mathrm{lim}}\frac{\sqrt{{x}^{2}+3x}}{x}=\underset{x\to \infty }{\mathrm{lim}}\frac{\sqrt{{x}^{2}+3x}}{\sqrt{{x}^{2}}}
Unimos las raíces del numerador con la del denominador.
\underset{x\to \infty }{\mathrm{lim}}\sqrt{\frac{{x}^{2}+3x}{{x}^{2}}}=\underset{x\to \infty }{\mathrm{lim}}\sqrt{\frac{{x}^{2}}{{x}^{2}}+\frac{3x}{{x}^{2}}}=\underset{x\to \infty }{\mathrm{lim}}\sqrt{1+\frac{3}{x}}
Evaluamos el límite.
\underset{x\to \infty }{\mathrm{lim}}\sqrt{1+\frac{3}{x}}=\sqrt{1+\frac{3}{\infty }}=\sqrt{1+0}=1
Finalmente:
\underset{x\to \infty }{\mathrm{lim}}\sqrt{1+\frac{3}{x}}=1
La respuesta correcta es el inciso b).
Reactivo 9
Dada la función f\left(x\right)={x}^{2}-1 , determine la expresión para calcular la derivada por definición.
- \underset{h\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{{h}^{2}-1-\left({x}^{2}-1\right)}{h}
- \underset{h\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{{\left(x+h\right)}^{2}-1-\left({x}^{2}-1\right)}{h}
- \underset{h\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{{h}^{2}-1}{h}
Solución:
La derivada por definición de una función se obtiene al resolver el siguiente límite:
\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}
En este caso f\left(x+h\right) se obtiene al sustituir x por x+h en la función.
f\left(x+h\right)={\left(x+h\right)}^{2}-1
Sustituimos en el límite.
\underset{h\to 0}{\mathrm{lim}}\frac{{\left(x+h\right)}^{2}-1-\left({x}^{2}-1\right)}{h}
Comparando con los incisos, indicamos como respuesta correcta al b).
Reactivo 10
Calcule la derivada de la función indicada.
f\left(x\right)=\frac{1}{\sqrt{2x-1}}
- {f}^{\text{'}}\left(x\right)=-\frac{1}{{\left(2x-1\right)}^{\frac{3}{2}}}
- {f}^{\text{'}}\left(x\right)=\frac{2x}{{\left(2x-1\right)}^{\frac{3}{2}}}
- {f}^{\text{'}}\left(x\right)={\left(2x-1\right)}^{\frac{3}{2}}
Solución:
Antes de comenzar a derivar, expresaremos al radical como una potencia.
f\left(x\right)=\frac{1}{\sqrt{2x-1}}=\frac{1}{{\left(2x-1\right)}^{1/2}}={\left(2x-1\right)}^{-1/2}
Ahora, aplicamos la fórmula de la derivada de una potencia.
{f}^{\text{'}}\left(x\right)={\left[{\left(2x-1\right)}^{-\frac{1}{2}}\right]}^{\text{'}}=-\frac{1}{2}{\left(2x-1\right)}^{\text{'}}{\left(2x-1\right)}^{-\frac{1}{2}-1}
Resolvemos la derivada indicada.
{f}^{\text{'}}\left(x\right)=-\frac{1}{2}{\left(2x-1\right)}^{\text{'}}{\left(2x-1\right)}^{-\frac{1}{2}-1}=-\frac{1}{2}\left(2\right){\left(2x-1\right)}^{-\frac{1}{2}-1}=-{\left(2x-1\right)}^{-\frac{1}{2}-1}
{f}^{\text{'}}\left(x\right)=-{\left(2x-1\right)}^{-\frac{3}{2}}=-\frac{1}{{\left(2x-1\right)}^{\frac{3}{2}}}
Finalmente:
{f}^{\text{'}}\left(x\right)=-\frac{1}{{\left(2x-1\right)}^{\frac{3}{2}}}
La respuesta correcta es el inciso a).
Reactivo 11
Uno de los resultados que se obtiene al calcular la derivada de una constante a partir de la regla general, es que la misma vale cero. ¿Cuál de los siguientes enunciados justifica correctamente este resultado?
- Porque solo se derivan funciones, no números reales
- Para calcular la derivada en ese caso, se debe usar la fórmula de la pendiente
- Porque las constantes tienen el mismo valor sin importar el punto que seleccionemos sobre el eje x
Solución:
Debemos recordar que la derivada mide la velocidad de cambio de una función respecto de su variable independiente, en un punto dado. Debido a que las constantes siempre tienen el mismo valor, no varían en ningún punto. Por esta razón, la derivada de una constante es cero.
Teniendo esto en cuenta y examinando a los incisos, concluimos que la respuesta correcta es c).
Reactivo 12
Asocie la función con su respectiva primera derivada.
- 1a, 2b, 3c
- 1c, 2b, 3a
- 1b, 2c, 3a
Solución:
Vamos a ir derivando cada una de las funciones en la columna izquierda para relacionarla con las derivadas de la derecha.
Primera función.
f\left(x\right)={x}^{2}\to {f}^{\text{'}}\left(x\right)=2x
1c.
Segunda función.
g\left(x\right)={e}^{2x}\to {g}^{\text{'}}\left(x\right)={\left(2x\right)}^{\text{'}}{e}^{2x}=2{e}^{2x}
2b.
Por descarte: 3a. Uniendo todas las respuestas parciales:
1c, 2b, 3a
Indicamos como respuesta correcta al inciso b).
Reactivo 13
Determine la derivada de la siguiente función.
f\left(x\right)=\frac{8}{{\mathrm{ln}}^{2}\left(x-1\right)+4}
- \frac{{\mathrm{ln}}^{2}\left(x-1\right)}{\mathrm{ln}\left(x-1\right)+4}
- \frac{1}{2\mathrm{ln}\left(x-1\right)}
- -\frac{16\mathrm{ln}\left(x-1\right)}{{\left[{\mathrm{ln}}^{2}\left(x-1\right)+4\right]}^{2}\left(x-1\right)}
Solución:
Antes de iniciar a derivar, vamos a reescribir el logaritmo al cuadrado del denominador.
f\left(x\right)=\frac{8}{{\mathrm{ln}}^{2}\left(x-1\right)+4}=\frac{8}{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4}
Ahora, iniciamos derivando con la fórmula de un cociente.
{f}^{\text{'}}\left(x\right)={\left[\frac{8}{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4}\right]}^{\text{'}}=\frac{{\left(8\right)}^{\text{'}}\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}-{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{\text{'}}\left(8\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}
La derivada del 8 es cero y para {\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4 aplicamos la propiedad de la derivada de una suma.
{f}^{\text{'}}\left(x\right)=\frac{0-\left\{{\left[{\mathrm{ln}\left(x-1\right)}^{2}\right]}^{\text{'}}+{4}^{\text{'}}\right\}\left(8\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}
Para el término {\mathrm{ln}\left(x-1\right)}^{2} iniciamos derivando como una potencia.
{f}^{\text{'}}\left(x\right)=\frac{-8\left\{{\left[{\mathrm{ln}\left(x-1\right)}^{2}\right]}^{\text{'}}+0\right\}}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}=\frac{-\left(8\right)\left(2\right){\left[\mathrm{ln}\left(x-1\right)\right]}^{\text{'}}\mathrm{ln}\left(x-1\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}
Finalmente, la derivada indicada se resuelve aplicando la fórmula del logaritmo.
{f}^{\text{'}}\left(x\right)=\frac{-16\left(\frac{1}{x-1}\right)\mathrm{ln}\left(x-1\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}
Acomodamos:
{f}^{\text{'}}\left(x\right)=-16\frac{\mathrm{ln}\left(x-1\right)}{\left(x-1\right){\left[{\mathrm{ln}}^{2}\left(x-1\right)+4\right]}^{2}}
Concluimos que la respuesta correcta es el inciso c).
Reactivo 14
Dada la siguiente gráfica y teniendo en cuenta el intervalo mostrado, indique el o los puntos donde la pendiente a la curva se anula.
- \left(0, 9\right);\left(4, 1\right)
- \left(9, 0\right);\left(1, 4\right)
- \left(-\infty , 3\right), \left(\infty , 3\right)
Solución:
Cuando la derivada de una función que no es una constante se anula, significa que la pendiente de la recta en dicho punto es cero. Una recta con pendiente cero, corresponde a una recta totalmente horizontal.
Examinando la figura, estos puntos son: el máximo relativo en \left(0, 9\right) y el mínimo relativo en \left(4, 1\right) .
Finalizamos la solución indicando como respuesta correcta al inciso a).
Reactivo 15
Calcula la tercera derivada de la siguiente función.
g\left(x\right)={e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
- {g}^{\text{'}}\left(x\right)=\frac{1}{x}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
- {g}^{\text{'}}\left(x\right)=-\frac{1}{2x}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)-1}
- {g}^{\text{'}}\left(x\right)=-\frac{{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}}{{x}^{2}+1}
Solución:
Para derivar la función del enunciado, debemos aplicar la regla de la cadena. En este caso, la función principal es la exponencial, por tanto, iniciamos derivando con la fórmula de la exponencial.
{g}^{\text{'}}\left(x\right)={\left[{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}\right]}^{\text{'}}={\left[{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)\right]}^{\text{'}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
A la derivada indicada le aplicamos la fórmula de la derivada de la tangente inversa.
{g}^{\text{'}}\left(x\right)=\frac{{\left(\frac{1}{x}\right)}^{\text{'}}}{1+{\left(\frac{1}{x}\right)}^{2}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
La última derivada indicada se resuelve aplicando la fórmula de la derivada de un cociente.
{g}^{\text{'}}\left(x\right)=\frac{{\left(\frac{1}{x}\right)}^{\text{'}}}{1+{\left(\frac{1}{x}\right)}^{2}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}=\frac{-\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}=-\frac{\frac{1}{{x}^{2}}}{\frac{{x}^{2}+1}{{x}^{2}}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
{g}^{\text{'}}\left(x\right)=-\frac{1}{{x}^{2}+1}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
Finalizamos indicando como respuesta correcta al inciso c).
Reactivo 16
Calcule la segunda derivada implícita de la siguiente curva.
\frac{{x}^{2}}{4}-\frac{{y}^{2}}{16}=1
- {y}^{\text{'}\text{'}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}
- {y}^{\text{'}\text{'}}=\frac{16{x}^{2}}{{y}^{3}}
- {y}^{\text{'}\text{'}}=\frac{1}{{y}^{3}}
Solución:
La derivada de una expresión es implícita, cuando tenemos términos no lineales con la variable dependiente y . En este caso, el término negativo tiene en el denominador {y}^{2} , esta es una forma no lineal de la variable dependiente.
Derivamos una primera vez:
\frac{2x}{4}-\frac{2y{y}^{\text{'}}}{16}=0
Simplificamos y despejamos a {y}^{\text{'}} .
\frac{x}{2}-\frac{y{y}^{\text{'}}}{8}=0\to {y}^{\text{'}}=\frac{4x}{y}
Derivamos una segunda vez:
{y}^{\text{'}\text{'}}=\frac{{\left(4x\right)}^{\text{'}}\left(y\right)-{\left(y\right)}^{\text{'}}\left(4x\right)}{{y}^{2}}=\frac{4y-4x{y}^{\text{'}}}{{y}^{2}}
Sustituimos {y}^{\text{'}}=\frac{4x}{y} .
{y}^{\text{'}\text{'}}=\frac{4y-4x\left(\frac{4x}{y}\right)}{{y}^{2}}=\frac{\frac{4{y}^{2}-16{x}^{2}}{y}}{{y}^{2}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}
Finalmente:
{y}^{\text{'}\text{'}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 17
Calcule la derivada de la siguiente función.
y=\frac{\mathrm{sin}x}{{\mathrm{cos}}^{2}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)
- {y}^{\text{'}}=2{\mathrm{sec}}^{3}x
- {y}^{\text{'}}=2{\mathrm{sec}}^{2}x
- {y}^{\text{'}}={\mathrm{sec}}^{3}x
Solución:
Antes de iniciar a derivar, vamos a simplificar aplicando identidades trigonométricas al primer término.
y=\frac{\mathrm{sin}x}{{\mathrm{cos}}^{2}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)=\frac{\mathrm{sin}x}{\mathrm{cos}x}\cdot \frac{1}{\mathrm{cos}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)=\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)
y=\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)
Iniciamos derivando con la propiedad de la derivada de una suma.
{y}^{\text{'}}={\left[\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)\right]}^{\text{'}}={\left(\mathrm{tan}x\mathrm{sec}x\right)}^{\text{'}}+{\left[\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)\right]}^{\text{'}}
Para el primer término aplicamos la derivada del producto. En el segundo, la derivada del logaritmo natural.
{y}^{\text{'}}={\left(\mathrm{tan}x\right)}^{\text{'}}\mathrm{sec}x+{\left(\mathrm{sec}x\right)}^{\text{'}}\mathrm{tan}x+\frac{{\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)}^{\text{'}}}{\frac{1+\mathrm{sin}x}{\mathrm{cos}x}}
{y}^{\text{'}}={\left(\mathrm{tan}x\right)}^{\text{'}}\mathrm{sec}x+{\left(\mathrm{sec}x\right)}^{\text{'}}\mathrm{tan}x+\frac{\mathrm{cos}x}{1+\mathrm{sin}x}{\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)}^{\text{'}}
Aplicamos la derivada de la tangente, de la secante y del cociente respectivamente.
{y}^{\text{'}}={\mathrm{sec}}^{2}x\mathrm{sec}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{\mathrm{cos}x}{1+\mathrm{sin}x}\cdot \frac{{\left(1+\mathrm{sin}x\right)}^{\text{'}}\left(\mathrm{cos}x\right)-{\left(\mathrm{cos}x\right)}^{\text{'}}\left(1+\mathrm{sin}x\right)}{{\mathrm{cos}}^{2}x}
{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{{\mathrm{cos}}^{2}x+\mathrm{sin}x\left(1+\mathrm{sin}x\right)}{\mathrm{cos}x}
{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{{\mathrm{cos}}^{2}x+\mathrm{sin}x+{\mathrm{sin}}^{2}x}{\mathrm{cos}x}
Aplicamos la identidad pitagórica.
{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{1+\mathrm{sin}x}{\mathrm{cos}x}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{\mathrm{cos}x}
{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\mathrm{sec}x
Extraemos factor común secante de los dos últimos términos.
{y}^{\text{'}}={\mathrm{sec}}^{3}x+\left({\mathrm{tan}}^{2}x+1\right)\mathrm{sec}x
Aplicamos la identidad pitagórica en términos de la secante y la tangente.
{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x
{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{sec}}^{2}x\mathrm{sec}x={\mathrm{sec}}^{3}x+{\mathrm{sec}}^{3}x=2{\mathrm{sec}}^{3}x
Finalmente:
{y}^{\text{'}}=2{\mathrm{sec}}^{3}x
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 18
Calcule la pendiente de la recta tangente a la curva f\left(x\right)={x}^{3}-1 , cuando x=0 .
- m=1
- m=3
- m=0
Solución:
Recordemos que la pendiente de la recta tangente a una curva se obtiene evaluando su derivada en el punto. Teniendo en cuenta lo anterior, debemos calcular la derivada de f\left(x\right) .
{f}^{\text{'}}\left(x\right)={\left({x}^{3}-1\right)}^{\text{'}}=3{x}^{2}
Evaluamos x=0 :
m=3{\left(0\right)}^{2}=0
El que la pendiente de una recta sea cero, indica que es una recta horizontal.
La respuesta correcta es el inciso c).
Reactivo 19
Sea xy-y=2x-1 la expresión de una curva, determine los puntos en los que la pendiente de la recta tangente a ella vale m=-\frac{1}{2} .
- \left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(\sqrt{2}-1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right)
- \left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(1-\sqrt{2},\frac{2\sqrt{2}-1}{\sqrt{2}}\right)
- \left(\sqrt{2},\frac{1}{\sqrt{2}}\right) y \left(\sqrt{2}-1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right)
Solución:
Iniciamos encontrando la derivada de la curva, recordemos que m={y}^{\text{'}} . Antes de derivar, vamos a extraer factor común y del miembro de la izquierda:
xy-y=2x-1\to y\left(x-1\right)=2x-1
y=\frac{2x-1}{x-1}
Esta expresión será más sencilla de derivar. Aplicamos la fórmula de la derivada de un cociente:
{y}^{\text{'}}={\left(\frac{2x-1}{x-1}\right)}^{\text{'}}=\frac{{\left(2x-1\right)}^{\text{'}}\left(x-1\right)-{\left(x-1\right)}^{\text{'}}\left(2x-1\right)}{{\left(x-1\right)}^{2}}
Resolvemos las derivadas indicadas.
{y}^{\text{'}}=\frac{2\left(x-1\right)-\left(2x-1\right)}{{\left(x-1\right)}^{2}}=\frac{2x-2-2x+1}{{\left(x-1\right)}^{2}}=-\frac{1}{{\left(x-1\right)}^{2}}
Ahora igualamos la derivada a la pendiente.
-\frac{1}{2}=-\frac{1}{{\left(x-1\right)}^{2}}
Para encontrar los puntos donde la pendiente es igual a -1/2 , resolvemos la ecuación anterior y evaluamos en la función original para encontrar las coordenadas en y .
{\left(x-1\right)}^{2}=2\to x-1=\pm \sqrt{2}
Obtenemos dos posibles resultados:
{x}_{1}=\sqrt{2}+1, {x}_{2}=1-\sqrt{2}
Evaluando en la función original:
{y}_{1}=\frac{2\left(\sqrt{2}+1\right)-1}{\sqrt{2}+1-1}=\frac{2\sqrt{2}+1}{\sqrt{2}}
{y}_{2}=\frac{2\left(1-\sqrt{2}\right)-1}{1-\sqrt{2}-1}=\frac{2\sqrt{2}-1}{\sqrt{2}}
Finalmente, los puntos donde la pendiente de la recta tangente a la curva es igual a -1/2 son:
\left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(1-\sqrt{2},\frac{2\sqrt{2}-1}{\sqrt{2}}\right)
Podemos comprobar sustituyendo los valores de x en la pendiente.
{y}_{1}^{\text{'}}=-\frac{1}{{\left(\sqrt{2}+1-1\right)}^{2}}=-\frac{1}{{\left(\sqrt{2}\right)}^{2}}=-\frac{1}{2}
{y}_{2}^{\text{'}}=-\frac{1}{{\left(1-\sqrt{2}-1\right)}^{2}}=-\frac{1}{2}
Concluimos el problema indicando como respuesta correcta al inciso b).
Reactivo 20
Dada la circunferencia centrada en el origen mostrada en la figura, determine las coordenadas de los puntos donde la pendiente vale \frac{1}{2} .
- \left(\frac{4}{\sqrt{5}},-\frac{8}{\sqrt{5}}\right) y \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)
- \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right) y \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)
- \left(\frac{4}{\sqrt{5}},-\frac{8}{\sqrt{5}}\right) y \left(-\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)
Solución:
Iniciamos encontrando la ecuación de la circunferencia. A partir de la imagen vemos que el radio es r=4 y que el centro \left(h, k\right)=\left(0, 0\right) .
{x}^{2}+{y}^{2}=16
Derivamos la expresión implícitamente y luego despejamos a {y}^{\text{'}} .
{x}^{2}+{y}^{2}=16\to 2x+2y{y}^{\text{'}}=0
{y}^{\text{'}}=-\frac{x}{y}
Podríamos comenzar despejar a y de la ecuación original y despejar así el valor de x y luego encontrar la coordenada vertical de los puntos; pero este procedimiento es largo. En su lugar, vamos a probar los puntos de cada inciso en la ecuación de la pendiente.
Si el resultado no es 1/2 , entonces pasamos al siguiente inciso.
Primer inciso.
{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{-\frac{8}{\sqrt{5}}}=\frac{1}{2}
{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{\frac{8}{\sqrt{5}}}=-\frac{1}{2}
El segundo punto da como resultado una pendiente negativa.
Segundo inciso.
Los puntos son iguales y ambas coordenadas son positivas, el resultado será negativo.
Tercer inciso.
{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{-\frac{8}{\sqrt{5}}}=\frac{1}{2}
{y}^{\text{'}}=-\frac{-\frac{4}{\sqrt{5}}}{\frac{8}{\sqrt{5}}}=\frac{1}{2}
El inciso c) es la respuesta correcta.
Reactivo 21
Resuelva el siguiente límite aplicando la regla de L´ Hopital.
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)
- L=1
- L=-1
- L=-2
Solución:
La regla de L’ Hopital nos dice que podemos resolver cualquier límite de una función racional con solo derivar el numerador y denominador a la vez. Primero debemos expresar a la función como un cociente, empleando el siguiente truco algebraico:
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)=\underset{x\to \infty }{\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{x-1}{x+1}\right)}{\frac{1}{x}}
Aplicando la regla de L’ Hopital:
\underset{x\to \infty }{\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{x-1}{x+1}\right)}{\frac{1}{x}}=\underset{x\to \infty }{\mathrm{lim}}\frac{{\left[\mathrm{ln}\left(\frac{x-1}{x+1}\right)\right]}^{\text{'}}}{{\left[\frac{1}{x}\right]}^{\text{'}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{\frac{x-1}{x+1}}}{-\frac{1}{{x}^{2}}}
Simplificamos antes de continuar derivando.
\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{\frac{x-1}{x+1}}}{-\frac{1}{{x}^{2}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{\left(x+1\right){\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{x-1}}{-\frac{1}{{x}^{2}}}=-\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}\left(x+1\right){\left(\frac{x-1}{x+1}\right)}^{\text{'}}}{x-1}
Para evitar complicar la expresión, resolveremos la derivada indicada aparte.
{\left(\frac{x-1}{x+1}\right)}^{\text{'}}=\frac{{\left(x-1\right)}^{\text{'}}\left(x+1\right)-{\left(x+1\right)}^{\text{'}}\left(x-1\right)}{{\left(x+1\right)}^{2}}=\frac{x+1-x+1}{{\left(x+1\right)}^{2}}=\frac{2}{{\left(x+1\right)}^{2}}
Sustituimos en el límite.
-\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}\left(x+1\right)\frac{2}{{\left(x+1\right)}^{2}}}{x-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{x}^{2}}{\left(x+1\right)}}{x-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{\left(x-1\right)\left(x+1\right)}
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{\left(x-1\right)\left(x+1\right)}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}
Evaluamos:
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}=\frac{\infty }{\infty }
Aplicamos de nuevo la regla de L’Hopital.
-2\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{2}}{{x}^{2}-1}=-2\underset{x\to \infty }{\mathrm{lim}}\frac{2x}{2x}=-2\underset{x\to \infty }{\mathrm{lim}}1
Evaluando:
-2\underset{x\to \infty }{\mathrm{lim}}1=-2
Finalmente:
\underset{x\to \infty }{\mathrm{lim}}x\mathrm{ln}\left(\frac{x-1}{x+1}\right)=-2
La respuesta correcta es el inciso c).
Reactivo 22
Calcule los valores de x para los extremos absolutos de la función real indicada a continuación en el intervalo \left[-2, 2\right] .
f\left(x\right)=\frac{x+2}{{e}^{x}}
- x=-1
- x=e
- x=\frac{1}{e}
Solución:
Los extremos de una función corresponden a los mínimos y máximos en un intervalo dado. Podemos calcular dichos puntos igualando a cero la derivada de la función. Nos quedaremos con aquellos extremos que se encuentren dentro del intervalo dado.
Derivada de la función.
{f}^{\text{'}}\left(x\right)={\left(\frac{x+2}{{e}^{x}}\right)}^{\text{'}}=\frac{{{e}^{x}\left(x+2\right)}^{\text{'}}-{\left({e}^{x}\right)}^{\text{'}}\left(x+2\right)}{{e}^{2x}}
{f}^{\text{'}}\left(x\right)=\frac{{e}^{x}-{e}^{x}\left(x+2\right)}{{e}^{2x}}=\frac{1-\left(x+2\right)}{{e}^{x}}=-\frac{x+1}{{e}^{x}}
{f}^{\text{'}}\left(x\right)=-\frac{x+1}{{e}^{x}}
Igualamos a cero la derivada.
-\frac{x+1}{{e}^{x}}=0
La fracción será cero sólo cuando el denominador se anule.
x+1=0\to x=-1
El extremo se encuentra dentro del intervalo.
La respuesta correcta es el inciso a).
Reactivo 23
Dada la función f\left(x\right)=2{x}^{3}+3{x}^{2}-12x+6 , calcule los intervalos de concavidad.
- \left(-\infty , -\frac{1}{2}\right)
- \left(-\infty , -1\right) y \left(1, \infty \right)
- \left(-\frac{1}{2}, \frac{1}{2}\right)
Solución:
Una función es cóncava en un punto si su segunda derivada es negativa. El intervalo de concavidad o convexidad, se obtiene mediante los puntos de inflexión de la función: puntos en los que la pendiente de la recta tangente cambia de signo.
El procedimiento a seguir es: calculamos la segunda derivada de la función, obtenemos los puntos de inflexión y evaluamos entre cuáles valores es negativa.
Segunda derivada de la función:
{f}^{\text{'}}\left(x\right)=6{x}^{2}+6x-12
{f}^{\text{'}\text{'}}\left(x\right)=12x+6
Igualamos a cero para encontrar el punto de inflexión.
12x+6=0\to x=-\frac{1}{2}
Sustituimos un valor de x antes y después de -\frac{1}{2} para comprobar en qué intervalo es negativa la segunda derivada.
Evaluando un punto antes.
{x}^{-}=-1\to {f}^{\text{'}\text{'}}\left(x=-1\right)=12\left(-1\right)+6=-6
La función es cóncava en el intervalo entre -\infty y -\frac{1}{2} sin incluir.
\left(-\infty , -\frac{1}{2}\right)
La respuesta correcta es el inciso a).
Reactivo 24
A partir de un tronco de sección perfectamente circular con radio igual a 3 m, se desea obtener una viga rectangular. ¿Cuáles deberían ser las dimensiones de la viga sobre la sección circular para que dicha viga tenga área máxima?
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=3,\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=2
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\frac{3\sqrt{2}}{2},\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=\frac{3\sqrt{2}}{2}
- \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\sqrt{2},\mathrm{ }\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=2
Solución:
El área de la viga rectangular se calcula como base b por altura a .
A=b\cdot a
Por otra parte, la diagonal del rectángulo debe ser igual al radio del tronco. Aplicando el teorema de Pitágoras:
{3}^{2}={a}^{2}+{b}^{2}
Despejamos una de las variables de la ecuación de la diagonal.
b=\sqrt{9-{a}^{2}}
Sustituimos en la función del área:
A=a\sqrt{9-{a}^{2}}
Con esta función, encontramos el máximo valor de altura derivando e igualando a cero.
\frac{dA}{da}={\left(a\sqrt{9-{a}^{2}}\right)}^{\text{'}}={\left(a\right)}^{\text{'}}\sqrt{9-{a}^{2}}+{\left(\sqrt{9-{a}^{2}}\right)}^{\text{'}}a
Resolvemos:
\sqrt{9-{a}^{2}}+\frac{1}{2}{\left(9-{a}^{2}\right)}^{\text{'}}{\left(9-{a}^{2}\right)}^{-\frac{1}{2}}=\sqrt{9-{a}^{2}}+\frac{1}{2}\left(-2a\right){\left(9-{a}^{2}\right)}^{-\frac{1}{2}}
\frac{dA}{da}=\sqrt{9-{a}^{2}}-\frac{a}{\sqrt{9-{a}^{2}}}=\frac{-2{a}^{2}+9}{\sqrt{9-{a}^{2}}}
Igualamos a cero.
\frac{-2{a}^{2}+9}{\sqrt{9-{a}^{2}}}=0\to -2{a}^{2}+9=0
Resolviendo nos queda:
{a}_{1}=\frac{3}{\sqrt{2}}, {a}_{2}=-\frac{3}{\sqrt{2}}
Nos quedamos con el resultado positivo.
a=\frac{3}{\sqrt{2}}
Sustituimos en la ecuación de la diagonal para despejar a b .
b=\sqrt{9-{\left(\frac{3}{\sqrt{2}}\right)}^{2}}=\sqrt{9-\frac{9}{2}}=\sqrt{\frac{18-9}{2}}=\frac{3}{\sqrt{2}}
Finalmente:
\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=\frac{3\sqrt{2}}{2}, \mathrm{a}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}=\frac{3\sqrt{2}}{2}
La respuesta correcta es el inciso b).
Reactivo 25
Calcular los valores de x en el intervalo \left[-1, 1\right] que satisfacen el teorema del valor medio para la función g\left(x\right)=-2{x}^{3}+{x}^{2}+x+1 .
Recuerde que:
{f}^{\text{'}}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}
- {c}_{1}=\frac{1}{6}, {c}_{2}=-\frac{1}{6}
- {c}_{1}=\frac{\sqrt{13}}{6}, {c}_{2}=-\frac{\sqrt{13}}{6}
- {c}_{1}=\frac{1-\sqrt{13}}{6}, {c}_{2}=\frac{1+\sqrt{13}}{6}
Solución:
En este caso, debemos obtener el valor de c a partir de la ecuación que se muestra en el enunciado. Encontramos a f\left(a\right) y f\left(b\right) sustituyendo los extremos del intervalo en la función.
a=-1\to f\left(-1\right)=3
b=1\to f\left(1\right)=1
Ahora, calculamos la derivada de f .
{f}^{\text{'}}\left(x\right)=-6{x}^{2}+2x+1\to {f}^{\text{'}}\left(c\right)=-6{c}^{2}+2c+1
Sustituimos todo en la ecuación del valor medio.
-6{c}^{2}+2c+1=\frac{1-3}{1+1}=-1
-6{c}^{2}+2c+2=0\to 3{c}^{2}-c-1=0
Aplicando la fórmula de la resolvente:
{c}_{1}=\frac{1-\sqrt{13}}{6}, {c}_{2}=\frac{1+\sqrt{13}}{6}
Indicamos como respuesta correcta al inciso c).
Reactivo 26
Dada la función f\left(x\right)={x}^{3}-2{x}^{2}+x+3 , calcule su diferencial.
- df=\left(3{x}^{2}-4x+1\right)dx
- df=dx
- df=\left({x}^{3}-2{x}^{2}+x\right)dx
Solución:
El diferencial de una función se encuentra aplicando la derivada de la siguiente forma:
\frac{df}{dx}={f}^{\text{'}}\left(x\right)\to df={f}^{\text{'}}\left(x\right)dx
Calculamos la derivada de la función en el diferencial:
df={\left({x}^{3}-2{x}^{2}+x+3\right)}^{\text{'}}dx
df=\left(3{x}^{2}-4x+1\right)dx
La respuesta correcta es la opción a).
Reactivo 27
La función de crecimiento de una población de bacterias viene dada por la siguiente expresión:
g\left(x\right)=\sqrt{x+1}
Si un grupo de investigadores ha encontrado una variación \mathrm{\Delta }x=0.5 cuando x=1 , ¿cuánto vale la variación de la población?
- dg\left(x\right)=\frac{8}{\sqrt{2}}
- dg\left(x\right)=\frac{\sqrt{2}}{8}
- dg\left(x\right)=0
Solución:
En términos geométricos, el diferencial dg de una función g\left(x\right) representa la variación que esta experimenta ante una variación en la variable independiente. El diferencial se calcula como:
dg={g}^{\text{'}}\left(x\right)dx
Derivamos a la función:
{g}^{\text{'}}\left(x\right)={\left(\sqrt{x+1}\right)}^{\text{'}}=\frac{1}{2}{\left(x+1\right)}^{\text{'}}{\left(x+1\right)}^{\frac{1}{2}-1}=\frac{1}{2\sqrt{x+1}}
Sustituyendo en el diferencial:
dg=\frac{1}{2\sqrt{x+1}}dx
Evaluamos.
dg=\frac{1}{2\sqrt{1+1}}\left(0.5\right)=\frac{1}{4\sqrt{2}}=\frac{\sqrt{2}}{8}
Finalmente, la población tiene una variación de:
dg=\frac{\sqrt{2}}{8}\approx 0.17677
La respuesta correcta es el inciso b).
Reactivo 28
Sea el diferencial de una función como df\left(x\right)=\left(3{x}^{2}+1\right)dx , ¿cuál de las siguientes opciones representa una familia de curvas a la que pertenece la función original?
- f\left(x\right)={x}^{3}+x+C
- f\left(x\right)={x}^{3}+x
- f\left(x\right)=3{x}^{2}+1+C
Solución:
Para deshacer el operador diferencial, debemos integrar en ambos miembros de la ecuación.
df\left(x\right)=\left(3{x}^{2}+1\right)dx\to \int df\left(x\right)=\int \left(3{x}^{2}+1\right)dx
f\left(x\right)=\int \left(3{x}^{2}+1\right)dx
Separamos en dos integrales simples aplicando la propiedad de la suma.
f\left(x\right)=\int \left(3{x}^{2}+1\right)dx=3\int {x}^{2}dx+3\int dx
Empleamos la fórmula de la integral de una potencia y del diferencial.
f\left(x\right)=\frac{3{x}^{2+1}}{2+1}+3x+C
La familia de curvas a la que pertenece la función original es:
f\left(x\right)={x}^{3}+3x+C
Indicamos como respuesta correcta al inciso a).
Reactivo 29
Calcula la siguiente integral indefinida.
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx
- I=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
- I=\frac{{x}^{2}}{2}-\frac{4}{x}+C
- I=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}
Solución:
Iniciamos la solución de la integral separando en fracciones simples.
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx=\int \frac{{x}^{3}}{{x}^{2}}dx-\int \frac{x}{{x}^{2}}dx+\int \frac{4}{{x}^{2}}dx
Simplificamos:
\int \frac{{x}^{3}}{{x}^{2}}dx-\int \frac{x}{{x}^{2}}dx+\int \frac{4}{{x}^{2}}dx=\int xdx-\int \frac{1}{x}dx+4\int \frac{1}{{x}^{2}}dx
Ahora, integramos aplicando las fórmulas inmediatas correspondientes.
\int xdx-\int \frac{1}{x}dx+4\int {x}^{-2}dx=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
Finalmente:
\int \frac{{x}^{3}-x+4}{{x}^{2}}dx=\frac{{x}^{2}}{2}-\mathrm{ln}\left|x\right|-\frac{4}{x}+C
La respuesta correcta es el inciso a).
Reactivo 30
Relacione cada integral inmediata con su primitiva.
- 1a, 2c, 3b
- 1c, 2b, 3a
- 1c, 2a, 3b
Solución:
Vamos a ir resolviendo cada una de las integrales en la columna izquierda para relacionarla con su respectiva primitiva en la columna derecha.
Primera integral.
\int {x}^{n}dx
Esta integral es la forma general de la integral de una potencia.
\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+C
1c.
Segunda integral.
\int {e}^{x}dx
Resolvemos aplicando la integral de una exponencial.
\int {e}^{x}dx={e}^{x}+C
2a.
Por descarte: 3b. Uniendo las respuestas parciales:
1c, 2a, 3b.
La respuesta correcta es el inciso c).
