En esta guía aprenderás a resolver problemas aplicando las reglas de los polinomios y realizando modelos matemáticos a partir de un escenario. En pocas palabras vamos a aplicar las matemáticas a problemas de la vida cotidiana.

En este caso, es claro que no profundizaremos a ese nivel en el modelado matemático. Utilizaremos algunos problemas cotidianos al estilo ¿Cuántas manzanas ha comprado Carmencita? Para resolverlos utilizando polinomios.
¿Lista o listo? ¡Comencemos!
¿Para qué sirven los modelos matemáticos?
El modelado matemático es un recurso esencial para dar vida a los descubrimientos y avances tecnológicos modernos. Se emplea con gran frecuencia en ciencias puras e ingeniería para establecer, de forma matemática, las relaciones de un hecho o recrear el comportamiento de algún fenómeno abstracto u observable.
Algunas de las técnicas empleadas por las farmacéuticas, pasan por recrear (modelar) de forma computacional al virus y así encontrar patrones sobre su comportamiento.
¿Qué necesito saber para recrear problemas con polinomios?
Como dije antes, el modelado matemático puede llegar a implicar cosas bastante complejas.
En este caso, solo será necesario saber sobre:
- Aritmética
- Polinomios
- Sistemas de ecuaciones
Y algo de esa intuición que has desarrollado en el estudio de las matemáticas.
Problemas con con polinomios
Con los siguientes ejercicios aprenderás a analizar problemas de la vida diaria y encontrar su solución empleando las matemáticas.
Problema1 Sistemas de ecuaciones
María compro por $18 un bolillo, una dona y un pastel. Pedro adquiere por $34 dos bolillos, tres donas y un pastel. Juan paga $54 pesos por cinco bolillos, tres donas y dos pasteles ¿Cuánto cuesta cada alimento?
- Bolillo 4, dona 6 y pastel 8
- Bolillo 3, dona 7 y pastel 8
- Bolillo 2, dona 6 y pastel 10
- Bolillo 2, dona 7 y pastel 9
Solución
Análisis: antes de pensar en escribir ecuaciones, es necesario entender lo que solicita el problema.
Hay que encontrar el precio individual de tres alimentos, específicamente: bolillo, dona y pastel. Esto da una idea que en el problema existen 3 variables cuyo valor, es desconocido.
Además, se especifica que tres niños adquirieron los alimentos en determinadas cantidades y han pagado ciertos montos por ellos. A partir de la compra de cada uno, podemos establecer las primeras relaciones entre las incógnitas del problema:
María
Bolillo + Dona + Pastel ha pagado $18
Pedro
2*Bolillo + 3*Dona + Pastel ha pagado $34
Juan
5*Bolillo + 3*Dona + 2*Pastel ha pagado $54
Cada una de las relaciones se asemeja a una ecuación con 3 incógnitas igualadas a un valor. Para simplificar la escritura, nos referiremos a cada variable como:
Bolillo = x, Dona = y, Pastel = z
Reescribiendo las ecuaciones:
María
x + y +z = 18
Pedro
2x + 3y + z = 34
Juan
5x + 3y + 2z = 54
Forman un sistema de 3 ecuaciones lineales con 3 incógnitas. Una vez resuelto el sistema se conocerá el valor de cada incógnita.
Existen diferentes métodos para resolver sistemas de ecuaciones lineales: igualación, sustitución, reducción o Gauss-Jordan. Puedes emplear cualquiera estudiado con anterioridad.
Esta vez, se resolverá el sistema mediante el método de reducción.
Modelo matemático del problema: sistema de 3 ecuaciones lineales con 3 incógnitas.
\begin{cases}M: x + y +z = 18\\P: 2x + 3y + z = 34\\J: 5x + 3y + 2z = 54\end{cases}
Aplicando el método de reducción:
Paso1: hacemos -2M + P.
-2M:-2x-2y-2z=-36
P:2x+3y+z=34
I: y-z=-2
Paso2: hacemos -5M + J.
-5M:-5x-5y-5z=-90
P:5x+3y+2z=54
II: y-z=-2
Paso3: hacemos -2I + II.
-2I:-2y-2z=4
II:2y+3z=36
\therefore5z=40\rightarrow z=8
Paso4: encontramos el valor de x y y .
Sustituimos z=8 en I para calcular a y:
y-(8)=-2\rightarrow y=8-2\\\therefore y=6
Sustituimos z=8 y y=6 en M para calcular a x:
x+(6)+(8)=18\rightarrow x=18-8-6\\\therefore x=4
De esta manera concluimos que:
x = Bolillo=\$4
y = Dona=\$6
z = Pastel=\$8
La respuesta correcta es la a).
Problema2
Un vecino vende un terreno rectangular en Acapulco y menciona que el área total es 480m^{2}, pero no recuerda las dimensiones de dicho terreno. Si el único dato que tiene es que el largo del terreno es tres veces el frente menos cuatro metros ¿Cuáles serán las dimensiones del terreno?
- Ancho 10, largo 48
- Ancho 15, largo 32
- Ancho 16/3, largo 90
- Ancho 40/3, largo 36
Solución
Análisis: para resolver este problema, solo hay que recordar la fórmula: A=frente*largo=f*l que sirve para calcular el área de un rectángulo.
Por otro lado, el frente f y el largo l del terreno son las variables del problema.
Lo único que conocemos de ellas es como se relacionan entre sí. De la frase: … el largo del terreno es tres veces el frente menos cuatro metros… se extrae la expresión:
l=3f-4
Que junto a la fórmula del área del rectángulo, se obtiene un sistema de 2 ecuaciones con 2 incógnitas:
\begin{cases}l=3f-4\\fl=480\end{cases}
El método para resolverlo será el de sustitución. Sustituimos la relación dada por el problema en la fórmula del área y luego se despeja el valor de f.
f(3f-4)=480\rightarrow3f^{2}-4f=480\\3f^{2}-4f-480=0
Se aplica la formula cuadrática para calcular a f:
\frac{-b\pm\sqrt{b^2-4ac}}{2a}
Para el caso de 3f^{2}-4f-480=0, el valor de los coeficientes es:
a=3;b=-4;c=-480
Sustituyendo y evaluando en la formula cuadrática se obtiene:
f=\frac{40}{3}\text{ y }f=-12
Por lógica, el único valor posible para el frente es f=\frac{40}{3}, debido a que no existen longitudes físicas negativas. Para calcular el valor del largo l, se sustituye el resultado obtenido para el frente en la relación dada:
l=3\left(\frac{40}{3}\right)-4=40-4=36
Conclusión: el frente del terreno mide f=\frac{40}{3} \text{m} y el largo 36 \text{m} . La respuesta correcta según el problema es la opción d).
Problema3
Si una viga de madera de 2m de largo se divide en dos partes que se encuentran en la proporción de 5:7, y la parte de menor longitud se corta a su vez en dos segmentos con razón de 2:3 ¿Cuánto mide la longitud de la parte más pequeña en que se cortó la viga?
- 2/3m
- 1/3m
- 1/5m
- 1/7m
Solución
Análisis: para visualizar de una forma más clara, hagamos un bosquejo de cómo quedaría dividida la viga.
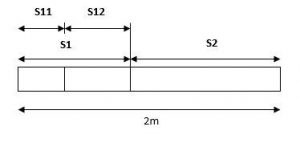
En el diagrama:
- S1 y S2 mitad pequeña y mitad larga de la viga
- S11 y S12 primer y segunda de la mitad más pequeña de la viga (S1)
Teniendo en cuenta que S1 y S2 son las mitades que juntas suman los 2m de la viga, es posible escribir:
s_{1}+s_{2}=2
Si la proporción entre las mitades es 5:7, obtenemos la relación:
\frac{s_{1}}{s_{2}}=\frac{5}{7}
Hay que aclarar que S1 debe ir en el numerador y S2 en el denominador porque el cociente 5:7 es menor a uno, lo que quiere decir que el dividendo es menor que el divisor. Ya que desde el inicio se asumió que S1 sería la mitad menor y S2 la mitad mayor, para que el resultado tenga concordancia hay que ordenarlos de esta manera.
Dicho lo anterior, nos queda un pequeño sistema de 2 ecuaciones con dos incógnitas. Para resolverlo se empleara el método por sustitución.
Despejamos S2:
\frac{s_{1}}{s_{2}}=\frac{5}{7} \rightarrow s_{2}=\frac{7}{5}s_{1}
Para luego sustituirlo en la primera ecuación:
\frac{7}{5}s_{1}+s_{1}=2\rightarrow \frac{12}{5}s_{1}=2\\\Rightarrow s_{1}=\frac{5}{6}
Podríamos calcular a S2 pero no es relevante para el ejercicio, ya que lo solicitado se encuentra en la mitad menor, es decir S1.
Ahora, toca hacer el mismo análisis para determinar el segmento más pequeño en la menor mitad. En la ilustración, se hace notar que S11 es el segmento menor de S1. Con el análisis hecho, queda calcular a S11.
s_{11}+s_{21}=\frac{5}{6} \text{ y }\frac{s_{11}}{s_{21}}=\frac{2}{3}
Despejamos a S21 y se sustituye en la ecuación s_{11}+s_{21}=\frac{5}{6}:
\frac{s_{11}}{s_{21}}=\frac{2}{3}\rightarrow s_{21}=\frac{3}{2}s_{11}\\ \text{sustituyendo: }s_{11}+\frac{3}{2}s_{11}=\frac{5}{6}\rightarrow \frac{5}{2}s_{11}=\frac{5}{6}\\ \therefore s_{11}=\frac{1}{3}
Conclusión: el valor de la longitud más pequeña en la viga es s_{11}=\frac{1}{3}m. La opción a seleccionar es la b).
Problema4
Luis viaja en su auto y recorre el día lunes 100 km en 2 horas. Se ha percatado que el día martes recorre 10 km en 9.6 minutos ¿En qué porcentaje Luis disminuye su tiempo al trasladarse?
- 10
- 15
- 20
- 30
Solución
Análisis: para calcular la diferencia porcentual, primero hay que relacionar los datos que proporciona el problema. Ten en cuenta que no se puede calcular de manera directa lo requerido con los tiempos dados, porque se tomaron en base a distancias distintas. Una para 100km y otra para 10km.
Una forma de relacionarlas, es mediante una equivalencia entre las distancias para así obtener un tiempo de referencia y luego compararlo con el que ha proporcionado el problema.
Partiendo del recorrido hecho el lunes tenemos que:
100km\rightarrow2h
Se convierte el tiempo a minutos para mantener unidades homogéneas:
100km\rightarrow120min
¿Cuánto tiempo debió tardar Luis en recorrer 10km?
100km\rightarrow120min\\ 10km\rightarrow x
x=\frac{10km*120min}{100km}=12min
Esto nos dice que: Luis, en referencia al primer recorrido debería tardarse 12 minutos en viajar 10 km. Si comparamos este resultado con lo señalado por el problema, vemos que Luis ha tardado menos tiempo: 9.6 minutos.
Con ambos valores, es posible calcular cual es la disminución porcentual del tiempo que ha tardado Luis (9.6 minutos) respecto al tiempo estimado (12 minutos).
\Delta\%=\frac{\text{tiempo teorico}-\text{tiempo real}}{\text{tiempo teorico}}*100
\Delta\%=\frac{12min-9.6min}{12min}*100=20\%
Conclusión: Luis ha disminuido el tiempo que tarda en trasladarse en un 20%. La opción a seleccionar es la c).

