¡Hola aspirante! En este tutorial vamos a resolver juntos los primeros 50 ejercicios del Simulacro de Matemáticas para el área Ciencias Médico Biológicas del Instituto Politécnico Nacional.

Esta lista contiene un resumen de los puntos clave acerca del examen de ingreso al IPN:
- Carreras ofertadas en IPN: 70+
- Porcentaje de aceptación: 20%
- Preguntas en el examen de admisión: 140 preguntas
- Nuevos temas: Historia e Inglés (reading comprehension)
- Tipo: selección múltiple
Estructura Examen IPN
La prueba de ingreso al IPN está compuesta de dos grandes bloques: conocimientos generales y conocimientos experimentales.
Antes, la cantidad de reactivos era la misma para todas las carreras, pero ahora varía según el área de estudio. Además, se incluyen preguntas de lectura en inglés y de historia de México. A continuación un resumen de los cambios:
- Cantidad de reactivos variable: la cantidad de reactivos ahora depende del área de la carrera.
- Nuevas asignaturas: se han agregado preguntas de Reading Comprehension e Historia de México.
- Más reactivos por responder: El examen para todas las carreras tendrá 140 reactivos, antes eran 130 reactivos.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Carreras de Ciencias Médico Biológicas
Las siguientes son las carreras que pertenecen al área de CMB:
- Licenciatura en Biología
- Licenciatura en Enfermería
- Licenciatura en Enfermería y Obstetricia
- Licenciatura en Nutrición
- Licenciatura en Odontología
- Licenciatura en Optometría
- Licenciatura en Psicología
- Licenciatura en Trabajo Social
- Médico Cirujano Homeópata
- Médico Cirujano Partero
- Químico Farmacéutico Industrial
- Químico Bacteriólogo y Parasitólogo
Temario Matemáticas Ciencias Médico Biológicas
Los temas para el área de Matemáticas en la prueba de ingreso cubren todos los conocimientos que recibiste en bachillerato acerca de esta materia.
- Razonamiento matemático.
- Álgebra.
- Geometría y trigonometría.
- Geometría analítica.
- Probabilidad y estadística.
- Cálculo diferencial
- Cálculo integral.
En algunos bachilleratos no se llevan los temas de cálculo que necesitarás para el examen, por esta razón, te dejo las siguientes recomendaciones para que domines fácilmente los temas de cálculo diferencial e integral:
- Repasa todos los temas de aritmética y refuerza las operaciones con radicales, potencias y fracciones.
- Es importante que conozcas a la perfección las identidades trigonométricas
- Comprende la teoría antes de pasar a los ejercicios
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos. Las siguientes son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve cada parte por tu cuenta antes de revisar el procedimiento.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo
Reactivo 1: sucesiones numéricas
Dada la siguiente sucesión numérica, obtenga el término faltante.
\frac{1}{5}, \frac{3}{5},1, -,\frac{9}{5}, \dots
- -1/5
- 3/5
- 7/5
- 5/7
Solución:
Para resolver este problema, primero debemos identificar qué tipo de sucesión es: aritmética o geométrica. Recordando rápidamente, en una progresión aritmética los números incrementan de forma constante, sumando al elemento {a}_{n} una diferencia d para obtener al elemento {a}_{n+1} .
Por otra parte, las progresiones geométricas se obtienen al multiplicar una razón r por {a}_{n} para obtener al término siguiente {a}_{n+1} , es decir, los incrementos entre dos números consecutivos no son constantes.
Podemos comprobar fácilmente si el problema trata de una sucesión aritmética, restando dos pares de números consecutivos, si la distancia entre estos pares es igual, entonces se trata de una progresión aritmética.
d={a}_{2}-{a}_{1}=\frac{3}{5}-\frac{1}{5}=\frac{2}{5}
Ahora lo hacemos con {a}_{3} y {a}_{2} .
d={a}_{3}-{a}_{2}=1-\frac{3}{5}=\frac{2}{5}
Confirmada la naturaleza de la sucesión, sólo nos queda sumar \frac{2}{5} al elemento {a}_{3} para obtener al elemento desconocido {a}_{4} .
{a}_{4}=1+\frac{2}{5}=\frac{7}{5}
Comparando con las opciones, concluimos que la respuesta correcta es el inciso c).
Reactivo 2: razonamiento matemático
Una empresa necesita cortar la materia prima para fabricar morrales, dichos patrones tienen forma de rectángulo con la característica de que el ancho mide el doble que el alto. Si el alto del patrón mide 0.15 m y el pliego de tela (materia prima) es cuadrado, ¿cuáles deberían ser sus dimensiones mínimas para extraer 100 patrones de un mismo pliego?
- 2.13
- 3
- 1.15
- 5
Solución:
Para resolver este problema (y cualquier otro similar), primero debemos ordenar la información que nos está indicando el enunciado para luego identificar las herramientas matemáticas que nos ayudarán a encontrar el valor solicitado.
El primer dato relevante que nos da el problema, es que los patrones que vamos a cortar del pliego de tela son rectangulares, es decir, tienen un ancho a y un alto h . Además, nos dice que el ancho a mide el doble que el alto h , esto puede escribirse como:
a=2h
Luego, nos indica que el alto del patrón h mide 0.15 metros, en consecuencia:
h=0.15 \mathrm{m}
a=2\left(0.15 \mathrm{m}\right)=0.3 \mathrm{m}
Sabemos que el pliego es cuadrado y debido a que sus dimensiones son desconocidas, llamaremos a su lado x . Con toda la información bien analizada, podemos calcular las dimensiones x del pliego igualando el área que ocuparían los 100 patrones con el área del pliego.
{A}_{pliego}=100\cdot {A}_{patron}
{x}^{2}=100\left(0.15\right)\left(0.3\right)\to x=\sqrt{4.5}
\therefore x=2.13 \mathrm{m}
Las dimensiones mínimas del pliego deben ser 2.13 por 2.13 metros para extraer los 100 patrones. Comparando con las opciones, la respuesta correcta es la a).
Reactivo 3: área sombreada
Calcule el área sombreada que se indica en la siguiente figura.
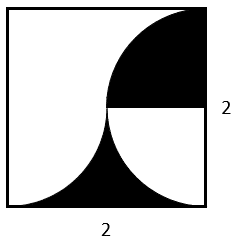
- 8-2\pi
- 4-2\pi
- 2-2\pi
- 2-\frac{\pi }{4}
Solución:
En el caso de tener secciones de la figura que describen contornos curvos, debemos identificar cómo podemos restar o sumar el área de sectores circulares (una circunferencia, media o cuarta) con partes rectangulares de las cuales podemos calcular su área.
Teniendo en cuenta lo anterior, podemos identificar o separar a las zonas oscuras como un cuarto de circunferencia, para la superior y dos cuartos de circunferencia para la inferior.
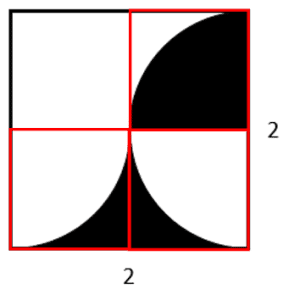
Ahora, el área sombreada total será igual a la suma del área sombreada superior más la inferior.
{A}_{T}={A}_{s}+{A}_{i}
El área superior es simplemente un cuarto de circunferencia.
{A}_{s}=\frac{\pi {r}^{2}}{4}
El radio es igual a 1, teniendo en cuenta las dimensiones del cuadrado externo.
{A}_{s}=\frac{\pi }{4}
El área sombreada inferior la podemos calcular como el área del rectángulo inferior de altura 1 y base 2, con el área de los dos cuartos de circunferencia, equivalentes al área de media circunferencia.
{A}_{i}=2-\frac{\pi {\left(1\right)}^{2}}{2}=2-\frac{\pi }{2}
Finalmente, sumamos las soluciones parciales.
{A}_{T}=2+\frac{\pi }{4}-\frac{\pi }{2}=2-\frac{\pi }{4}
Comparando con las opciones, la respuesta correcta es el inciso d).
Reactivo 4: sucesión numérica
La siguiente sucesión, corresponde con el número de aristas que se pueden trazar para conectar los n vértices de un polígono. Si tuviésemos uno con 20 vértices, ¿cuántas aristas se necesitan para conectarlos entre sí?
3, 6, 10, 15, 21, 28, \dots
- 200
- 190
- 180
- 220
Solución:
En este caso, debemos determinar una fórmula que nos permita calcular el número de aristas que se pueden trazar para conectar los vértices de un polígono cualquiera. Comencemos por mencionar, que dicho total de aristas es la suma de las aristas principales con las diagonales.
A={A}_{p}+D
Un polígono tendrá tantas aristas principales como vértices. Si el número de vértices es n :
A=n+D
Por otra parte, un polígono tendrá diagonales si posee 4 vértices o más.
D=n-3
Ahora, multiplicamos por n para obtener el total de diagonales.
D=n\left(n-3\right)
Este resultado nos da dos diagonales por cada par de vértices, pero solo necesitamos 1, dividimos entre dos.
D=\frac{n\left(n-3\right)}{2}
Sumamos las soluciones.
A=n+\frac{n\left(n-3\right)}{2}=\frac{n\left(n-1\right)}{2}
Finalmente, sustituimos 20 y obtenemos:
A\left(20\right)=\frac{20\left(20-1\right)}{2}=190 \mathrm{a}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{s}
Se necesitan 190 aristas para conectar sin falta ni repeticiones a 20 vértices. La respuesta correcta se encuentra en el inciso b).
Reactivo 5: término general de la sucesión
Determine el término general de la siguiente sucesión.
\frac{2}{3},\frac{5}{6}, 1,\frac{7}{6},\frac{4}{3},\frac{3}{2}, \dots
- \left\{\frac{2}{3}-\frac{1}{6}\left(n-1\right)\right\}
- \left\{\frac{2}{3}+\frac{1}{6}\left(n-1\right)\right\}
- \left\{\frac{1}{3}-\frac{1}{6}\left(n-1\right)\right\}
- \left\{\frac{1}{3}+\frac{1}{6}\left(n-1\right)\right\}
Solución:
Como en toda sucesión numérica, comenzamos por comprobar si se trata de una progresión aritmética o de una progresión geométrica. Restamos dos pares de términos consecutivos:
b={a}_{2}-{a}_{1}=\frac{5}{6}-\frac{2}{3}=\frac{1}{6}
Hacemos lo mismo con {a}_{2} y {a}_{3} .
b={a}_{3}-{a}_{2}=1-\frac{5}{6}=\frac{1}{6}
Se trata de una progresión aritmética.
{a}_{n}={a}_{1}+\left(n-1\right)b
En este caso, {a}_{1} es \frac{2}{3} . Sustituyendo obtenemos:
{a}_{n}=\left\{\frac{2}{3}+\frac{1}{6}\left(n-1\right)\right\}
Comprobamos nuestro resultado rápidamente.
{a}_{1}=\frac{2}{3}+\left(1-1\right)\cdot \frac{1}{6}=\frac{2}{3}
{a}_{2}=\frac{2}{3}+\left(2-1\right)\cdot \frac{1}{6}=\frac{5}{6}
{a}_{3}=\frac{2}{3}+\left(3-1\right)\cdot \frac{1}{6}=1
⋮
Concluimos indicando como respuesta correcta la opción b).
Reactivo 6: completar la sucesión
Complete los espacios restantes en la siguiente sucesión numérica.
-\frac{1}{6}, -,\frac{1}{2}, -,\frac{7}{6}, \dots
- \frac{1}{6},\frac{5}{6}
- \frac{1}{3},\frac{5}{3}
- \frac{2}{3},\frac{5}{3}
- \frac{5}{6},\frac{1}{3}
Solución:
Por la forma en la que crecen los términos de la sucesión, podemos estar seguros de que se trata de una progresión aritmética. Siguiendo esta idea y teniendo en cuenta que {a}_{1}=-\frac{1}{6} , podemos encontrar a b empleando la ecuación del término general.
{a}_{n}=\left\{{a}_{1}+b\left(n-1\right)\right\}
Vamos a igualar la ecuación a un término conocido y distinto a n=1 , de tal forma que podamos despejar a b .
{a}_{3}=\frac{1}{2}=-\frac{1}{6}+\left(3-1\right)b
Despejando:
b=\frac{1}{3}
Finalmente:
{a}_{n}=\left\{-\frac{1}{6}+\left(n-1\right)\cdot \frac{1}{3}\right\}
Sustituimos las posiciones faltantes:
{a}_{2}=\frac{1}{6}
{a}_{4}=\frac{5}{6}
Comparando con las opciones, la respuesta correcta se encuentra en el inciso a).
Reactivo 7: espacios en la sucesión
Complete los espacios restantes en la siguiente sucesión numérica.
-,\frac{3}{40}, -\frac{1}{20}, -\frac{7}{40}, \dots
- \frac{1}{5}
- -\frac{1}{5}
- \frac{2}{5}
- -\frac{2}{5}
Solución:
Este problema es relativamente sencillo de resolver, ya que, examinando cómo decrecen los elementos, podemos estar seguros que se trata de una progresión aritmética. El término faltante es el inicial {a}_{1} , el cual podemos obtener restándole (o sumándole según sea el caso) b al término {a}_{2} .
Obtenemos b restando dos términos consecutivos.
b=-\frac{1}{20}-\frac{3}{40}=-\frac{1}{8}
Debido a que b es negativo, para encontrar el término {a}_{1} le sumamos b al término {a}_{2} .
{a}_{1}=\frac{3}{40}+\frac{1}{8}=\frac{1}{5}
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 8: serie gráfica
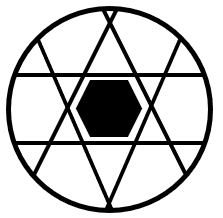
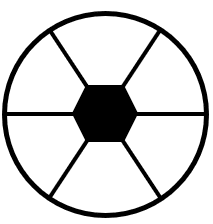
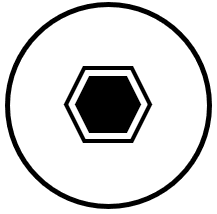
Identificar la figura que completa la serie gráfica.
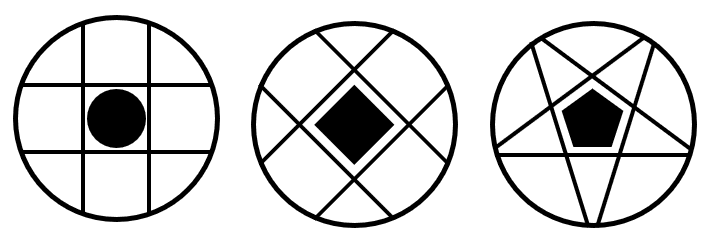
Solución:
Para resolver series gráficas, debemos identificar qué elementos cambian y la forma en la que cambian. Lo primero que podemos notar, es que tanto el contorno circular como los colores permanecen constantes, así que no hay ninguna alteración en estos dos aspectos.
Por otra parte, la figura central y las líneas internas que, vendrían a ser cuerdas dentro de la circunferencia, cambian de forma conjunta. Primero un círculo y 4 cuerdas, luego un rombo y 4 cuerdas paralelas a sus lados, la siguiente figura es un pentágono y 5 cuerdas dentro de la circunferencia paralelas a dichos lados.
Siguiendo esta secuencia, la siguiente figura tiene que ser un hexágono con 6 cuerdas cada una paralela a uno de sus lados. La única figura que cumple con esto y mantiene los colores es la del inciso a).
Reactivo 9: términos de la sucesión
Identifica los siguientes 2 términos de la sucesión.
-4, -\frac{9}{2}, -5, -\frac{11}{2}, -6, \dots
- -\frac{13}{3}, -7
- \frac{13}{3}, 7
- -\frac{13}{3}, -7
- \frac{13}{3}, 7
Solución:
Si examinamos detenidamente cómo cambian los términos, nos daremos cuenta que disminuyen de forma constante, donde la diferencia entre cualesquiera dos términos consecutivos es b=-\frac{9}{2}+4=-\frac{1}{2} . Teniendo esto en cuenta y tomando el último término que nos deja la sucesión, podremos obtener los dos siguientes.
{a}_{6}={a}_{5}-\frac{1}{2}=-6-\frac{1}{2}=-\frac{13}{2}
{a}_{7}={a}_{6}-\frac{1}{2}=-\frac{13}{2}-\frac{1}{2}=-7
Comparando con las opciones, concluimos que la respuesta correcta se encuentra en el inciso a).
Reactivo 10: rezonamiento espacial
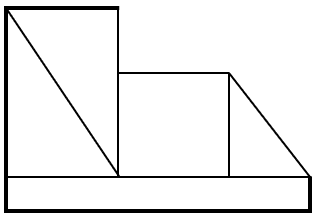
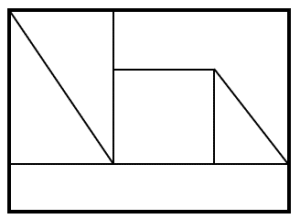
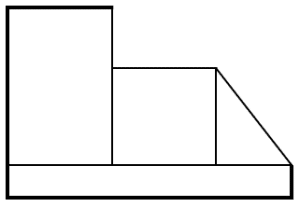
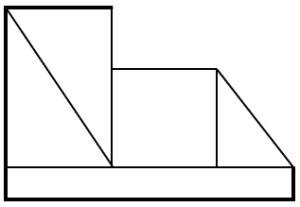
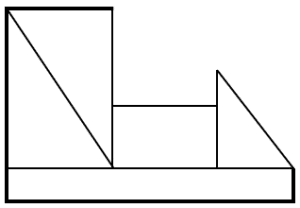
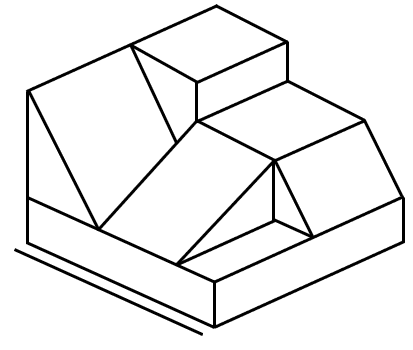
Identifique la figura que corresponde con la visión frontal de la siguiente imagen.
Solución:
Para resolver estos problemas de perspectiva, es necesario identificar la cara que debemos determinar y plasmar en un plano como se vería la figura tridimensional vista desde esa cara.
De antemano, sabemos que el borde externo es escalonado, por lo que podemos descartar la primera imagen, ya que esta supone que hay un marco rectangular.
Ahora, en el fondo quedarían dos rectángulos, uno más grande que otro y el primero tendría una línea en diagonal que va de izquierda a derecha, correspondiente a la rampa.
Por último, la figura termina en la parte derecha con otra línea en diagonal que va desde la parte superior del rectángulo menor, hasta la base de la figura. Examinando las opciones, podemos concluir que la respuesta correcta es el inciso c).